基于3种机器学习模型的岩爆类型预测
詹术霖, 黄明清, 陈霖, 蔡思杰
(1. 福州大学紫金地质与矿业学院, 福建 福州 350108; 2. 紫金矿业集团股份有限公司, 福建 厦门 361016)
0 引言
岩爆, 是一种岩体中聚积的弹性变形势能在一定条件下突然猛烈释放, 导致岩石爆裂并弹射出来的现象, 不仅影响工程进度, 更是给地下工程作业人员带来巨大安全隐患, 造成不必要的损失[1-2]. 随着矿山开采和地下工程规模的不断扩大, 岩爆问题日益突出, 因此, 探明岩爆类型预测方法显得尤为重要.
岩爆类型预测是防治和控制岩爆灾害提前发生最有效的方式之一, 主要分为单因素预测方法和多因素综合预测方法. 单因素预测方法[3-5]大多基于特定的工程背景, 因此单因素预测方法的准确度通常较低, 泛化能力较弱[6]. 多因素综合预测方法主要有数学方法与智能算法两类. 数学方法[7-9]通常需要人为确定指标权重, 受人为主观影响明显, 无法客观预测岩爆类型[10], 而智能算法中的机器学习算法具有模型泛化能力强和适用于小样本等优点, 引起国内外学者的兴趣.
李明亮等[2]采用6种机器学习算法结合交叉验证建立岩爆预测模型, 但未将训练集与测试集分开进行标准化处理. 汤志立等[6]对原始数据集进行预处理后建立9个岩爆预测模型, 预测结果好于传统理论判据预测结果. 吴顺川等[11]基于岩爆案例数据建立PCA-PNN岩爆类型预测模型, 模型收敛速度快, 预测结果合理. 田睿等[12]以独立4因素为训练样本构建DA-DNN模型, 模型避开指标权重的确定问题, 实现更加客观的预测岩爆类型. Zhou等[13]采用10种有监督学习算法进行岩爆类型预测, 并采用准确率与Kappa等指标对比不同算法的预测性能. 已有研究中, 在对训练集与测试集预处理时往往存在训练集信息泄露, 模型的可靠性与泛化能力不足.
为了提高模型预测的可靠性与准确率, 本研究通过文献检索建立397组岩爆工程案例样本, 并选用最近邻(KNN)、 支持向量机(SVM)、 决策树(DT)等3种在岩爆类型分类性能上表现较好的机器学习算法作为预测模型进行训练, 通过规范化的数据预处理方式避免训练集信息泄露, 提高预测模型的可靠性. 首先, 分析主成分分析法(principal component analysis, PCA)对3种机器学习模型的适用性, 并通过可视化降维后的数据分布解释主成分分析失效原因; 其次, 为降低原始数据集的不平衡性, 采用SMOTE过采样进行预处理, 并与原始数据集预测效果进行对比; 最后, 分析3种机器学习模型低估或高估岩爆类型的情况, 并对3种机器学习模型的分类性能进行评估, 选出最适合岩爆类型预测的机器学习模型.
1 数据与方法
1.1 指标分析与数据来源
1) 指标分析. 岩爆评价指标的选取是岩爆类型预测的关键[12], 以往研究通常选取岩石的最大切向应力σθ、 单轴抗压强度σc、 单轴抗拉强度σt与弹性能量指数Wet作为岩爆评价指标. 汤志立等[6]还考虑了深度, 但深度与单轴抗压强度等指标具有一定的相关性[14-15], 故深度指标的引入无法为数据集提供更多信息. 同时, 为了能够从不同角度反映岩爆特征信息, 在σθ、σc与σt等指标的基础上构建组合式指标, 例如最大切向应力与单轴抗压强度之比Scf(σθ/σc)、 脆性系数B1(σc/σt)、 应力系数B2[(σc-σt)/(σc+σt)]. 因此, 本研究共选取上述7个指标作为岩爆类型预测指标. 岩爆预测结果通常根据岩爆发生的剧烈程度及破坏特征, 将岩爆划分为4类: 无岩爆(none, N)、 弱岩爆(light, L)、 中等岩爆(moderate, M)与强岩爆(strong, S).
2) 数据来源. 为了衡量各种机器学习算法的性能与适用性, 本研究使用的397组岩爆案例均来自于已发表文章, 其中331组来自Zhou等[16]、 46组来自Dong等[17]、 20组来自周科平等[10]. 将岩爆数据集的各类别分别按8∶2的比例随机分为训练集(317组)与测试集(80组)两个子集.
1.2 数据描述与数据预处理
1) 数据描述. 对于岩爆评价指标, 397组岩爆案例的7个评价指标统计参数见表1. 从该表可以看出, 随着指标σθ、σc、σt与Wet均值的增加, 岩爆类型总体逐渐从N变化到S, 但4个指标标准差较大, 且Scf、B1与B2这3个指标与岩爆类型并无明显规律, 增加了岩爆类型预测的难度, 无法直接根据单一指标判定岩爆类型.
从岩爆预测指标相关性矩阵(表2)可以看出, 部分预测指标间具有较强的相关性, 这是由于传统岩爆判据基于围岩应力参数进行预测, 而Scf、B1与B2是基于围岩应力参数进行组合构建. 因此, 有必要尝试对7个岩爆预测指标进行PCA预处理, 消除指标间的相关性, 并将预测结果与原始数据集的预测结果进行对比.
从岩爆样本分布(图1)可以看出, 岩爆类型为中等岩爆的数量最多, 为140例; 类型为强岩爆与无岩爆的数量最少, 分别为69例与73例, 样本存在一定的不均衡性. 而机器学习模型通常以最大化总体准确率为目标函数, 不平衡问题会导致算法过多关注多数类, 降低模型对少数类的分类性能. 因此, 本研究采用SMOTE过采样对训练集进行预处理, 消除样本不均衡性.
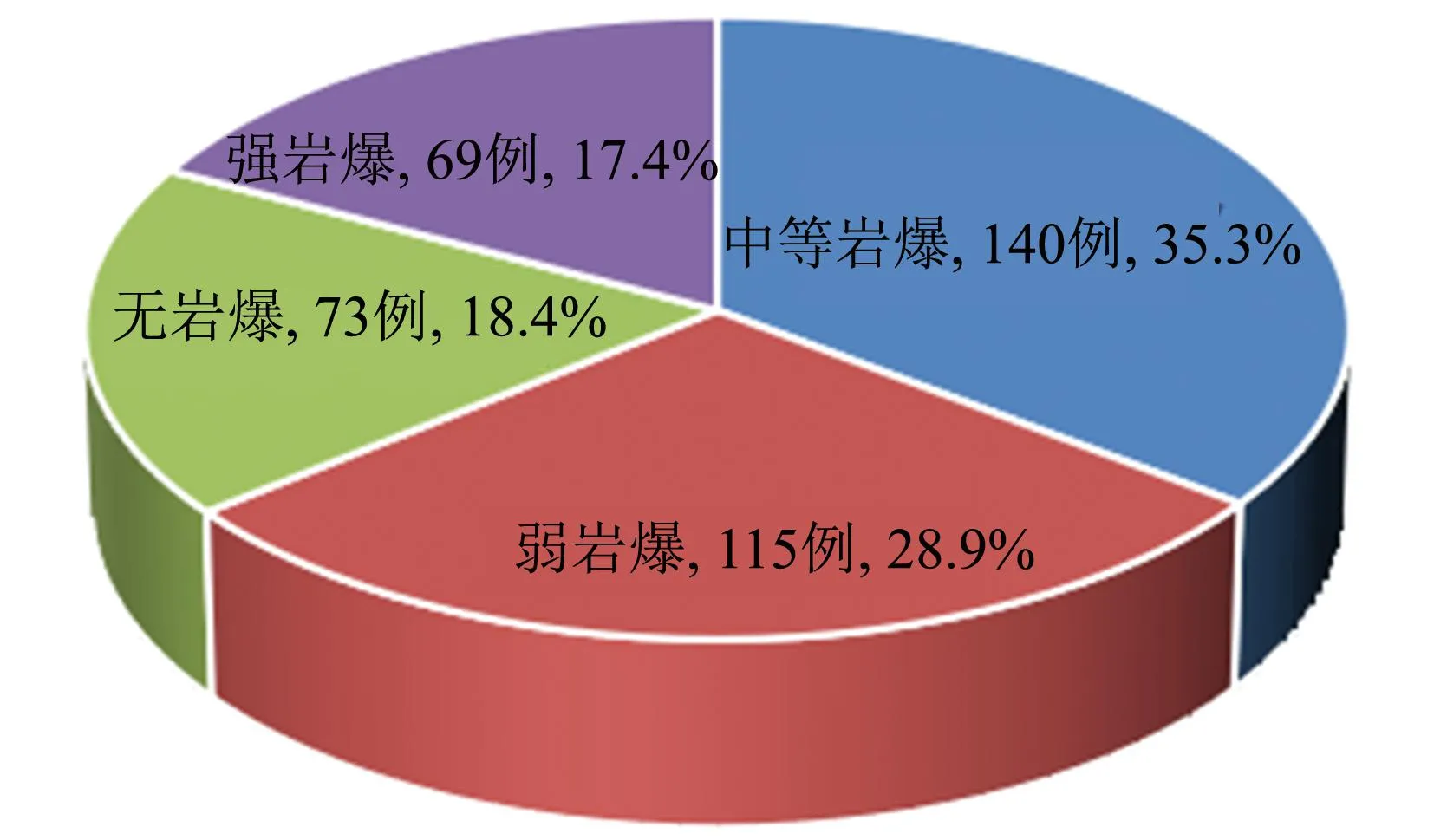
图1 岩爆样本分布Fig.1 Distribution of rockburst samples
2) 数据标准化. 为消除各指标量纲不一致对模型预测的影响, KNN与SVM模型需要在输入岩爆预测指标前对数据进行标准化处理, 即首先对训练集进行标准化, 再利用训练集的均值与标准差, 对测试集进行标准化. 而对于DT模型, 特征的划分与信息熵的变化有关, 与指标特征大小无关, 故该模型无需对数据进行标准化.
3) 主成分分析PCA. 从表2可以看出, 部分指标之间相关性较强, 如最大切向应力与Scf相关系数为0.77、B2与B1相关系数为0.75, 岩爆预测指标之间存在较为明显的相关性. 因此, 在模型训练前可以采用PCA对训练集进行降维处理.
4) 过采样SMOTE. 通过随机采样训练集中少数类生成的合成样本而非实例的副本, 从而缓解过拟合问题, 并且不会损失有价值的信息. 故本研究选用SMOTE过采样技术对不平衡数据集进行预处理.
1.3 机器学习算法
机器学习算法类型较多, 其中, 偏最小二乘判别分析、 朴素贝叶斯与AdaBoost等有监督机器学习算法预测准确率低于50%; 因此, 本研究只采用准确率较高的KNN、 SVM与DT模型实现对岩爆类型的预测.
1.4 模型评价方法与指标
1) 模型参数优化. 为了提升模型的泛化能力, 防止模型过拟合, 在训练集上采用5折交叉验证的方法确定模型参数. 同时, 模型训练过程中采用网格搜索进行模型参数优化, 以获得5折交叉验证下算法的最优参数.
2) 性能评价指标. 为了评估本研究所建立的3种分类模型的泛化性能, 借助准确率、 精确率、 召回率与F1值等指标衡量模型泛化能力. 对于多分类问题, 还涉及宏平均与微平均指标.
2 实验结果与讨论
2.1 PCA及SMOTE适用性分析
1) PCA对3种机器学习模型的预测准确度对比. 采用训练集的317组样本进行主成分分析, 各主成分方差贡献率及累计贡献率见表3. 由于前3个主成分的累计贡献率为85.39%, 故将前3个主成分作为模型的输入. 表4为对应主成分系数矩阵.
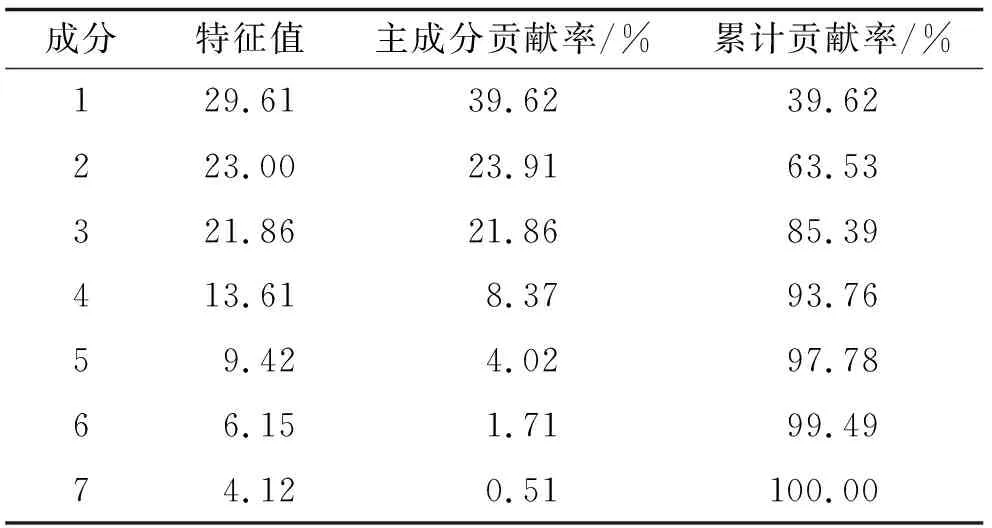
表3 主成分分析处理结果Tab.3 Results of principal component analysis
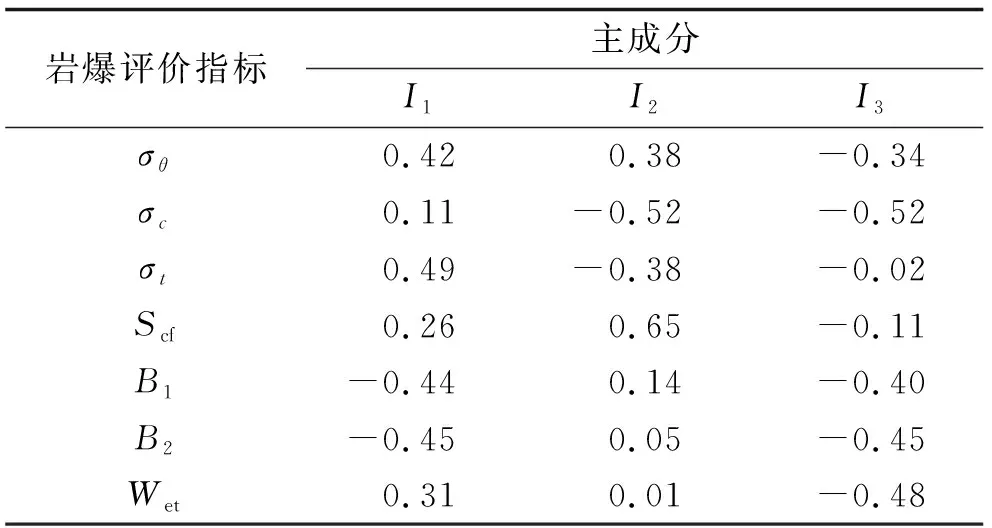
表4 主成分系数矩阵Tab.4 Principal component coefficient matrix
根据主成分系数矩阵(表4), 可以得出主成分I1、I2、I3与7个岩爆预测指标之间的关系为
I1=0.42σθ+0.11σc+0.49σt+0.26Scf-0.44B1-0.45B2+0.31Wet
(1)
I2=0.38σθ-0.52σc-0.38σt+0.65Scf+0.14B1+0.05B2+0.01Wet
(2)
I3=-0.34σθ-0.52σc-0.02σt-0.11Scf-0.40B1-0.45B2-0.48Wet
(3)
利用式(1)~(3)对80组测试集数据进行线性转换后作为模型的输入进行岩爆类型预测, 有无采用PCA预处理的模型预测准确率如表5所示. 从表5可以看出, PCA预处理略微提高SVM模型的预测准确率, 降低了KNN与决策树模型在测试集上的预测准确率. 因此, 主成分分析对该样本集提高模型预测准确率并无显著效果.
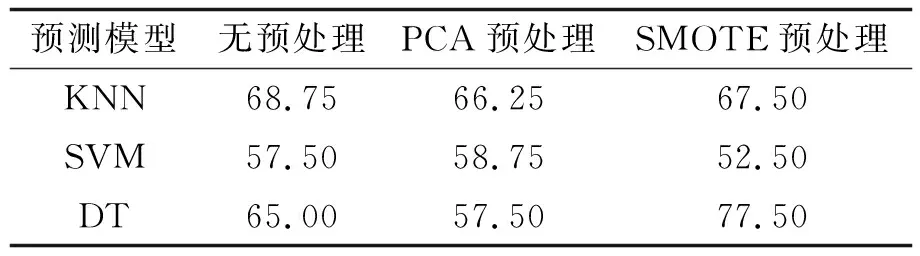
表5 预处理对模型预测准确率对比Tab.5 Comparison of data preprocessing on model prediction accuracy (%)
原始数据集存在7个岩爆预测指标, 采用PCA预处理可以在保留原始信息的前提下将7维数据通过线性转换投影到低维空间, 降维后的数据集如图2所示.

图2 降维后样本分布图Fig.2 Sample distribution after dimension reduction
从图2可以看出, 无论是二维还是三维空间, 数据集存在较大扰动, 不同岩爆类型的样本之间不具有较为明显的分类边界, 因此PCA无法有效提高岩爆类型预测准确率.
2) 过采样SMOTE对3种机器学习模型的预测准确度对比. 采用SMOTE过采样算法后, 样本量由原训练集的317组增加至448组(4类岩爆类型均为112个). 从采样前后部分岩爆预测指标箱型图(图3)可以看出, 过采样前后数据集整体分布较为一致, 故可以采用过采样后的样本对机器学习模型进行训练. 从SMOTE对3种机器学习模型预测准确率对比表(表5)可以看出, SMOTE过采样预处理可以明显提升DT模型算法的准确率, 预测准确率从原始数据集的65%提高至过采样预处理后的77.5%.
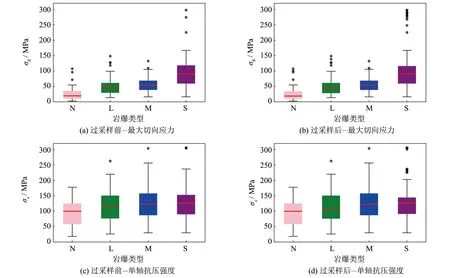
图3 过采样前后部分岩爆评价指标箱型图Fig.3 Box diagram of some rockburst evaluation indicators before and after oversampling
2.2 3种机器学习模型预测结果分析
2.2.1模型训练与预测
根据2.1节分析可知, SMOTE过采样能够明显提高决策树模型的预测准确率(A), 故本文采用SMOTE算法预处理的SMOTE-DT模型及仅对原始数据集进行标准化处理的KNN、 SVM模型.
结合5折交叉验证与模型参数优化, 可得各模型在不同参数下的5折交叉验证结果如图4所示. 从图4可以看出, SVM模型中的惩罚系数(C)的最佳值为256、 SMOTE-DT模型中决策树最大深度(dmax)的最佳值为10、 KNN模型中的参考最相似标签值的个数k_neighbor(K)最佳值为1.


图4 3种机器模型五折交叉验证结果Fig.4 5-fold cross validation results of three machine models
2.2.2模型预测结果准确率分析
利用训练后的模型对测试集进行测试, KNN、 SVM、 SMOTE-DT模型预测准确率分别为68.75%、 57.50%与77.50%, 远高于4分类问题随机分类时的25%. 为了更加直观看出3种机器模型对4种岩爆类型预测情况, 将N、 L、 M与S类型编号为1、 2、 3、 4, 采用(预测类型-真实类型)作为纵坐标, 测试集样本序号作为横坐标, 绘制3种机器模型的预测结果, 如图5~7所示.
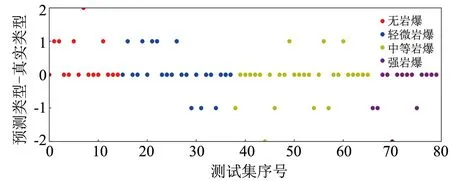
图5 KNN预测结果Fig.5 KNN prediction results
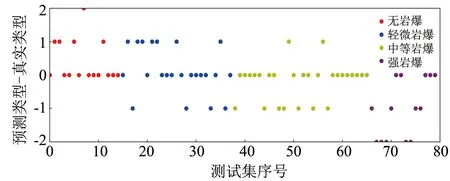
图6 SVM预测结果Fig.6 SVM prediction results
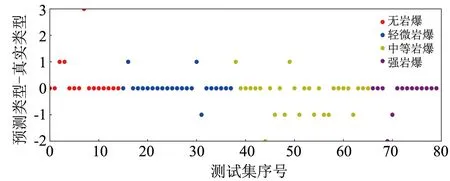
图7 SMOTE-DT预测结果Fig.7 SMOTE-DT prediction results
从图5~7可以看出, 3种模型高估岩爆类型的次数分别为13、 14与7次, 低估岩爆类型的次数分别为12、 20、 11次. 高估岩爆类型虽然会造成一定的资源浪费, 但生产安全性可以得到较好的保障, 而低估岩爆类型不仅会影响施工进度, 而且容易造成人员伤亡及经济损失. 总之, SMOTE-DT模型的预测准确性与安全保障性均优于KNN与SVM模型.
2.2.3不同类别岩爆分类性能
为获取3种预测模型对不同类别岩爆样本的分类性能, 采用精确率P、 召回率R、F1值、 宏平均与微平均指标进行计算, 3种机器学习算法性能评价如表6所示. 从宏平均与微平均指标来看, SMOTE-DT模型相较于KNN与SVM模型对不同类别岩爆样本的分类能力较强, KNN模型次之, SVM模型表现最差. 从3种算法的性能指标可知, SVM模型的强岩爆类型召回率低于50%, 说明被SVM模型预测为强岩爆类型的测试集中有50%以上实际并非强岩爆类型, 模型对于强岩爆类型的预测十分不可靠. SMOTE-DT模型在4种岩爆类型上的分类性能均优于KNN与SVM模型, 同时SMOTE-DT模型对于4种岩爆类型的F1值均大于0.7, 分类性能稳定可靠.
3 工程应用案例
3.1 工程概况及地质条件
山西紫金金矿为2016年发现的大型斑岩型矿体, 主矿体为BK1、 BK2矿体, 矿体中间厚大连续, 开采标高610~950 m, 最低生产中段610 m中段开采深度大于700 m, 接近于深部开采. 因此, 强烈的开采扰动会对深部岩体产生较强烈的影响, 尤其是硬岩岩爆与斑岩型矿体的开拓、 开采、 支护等生产安全密切相关.
3.2 岩爆类型预测
采用3种机器学习模型对山西紫金岩爆类型进行预测. 为了确定山西紫金的岩爆类型, 在矿山目前已开拓的830、 890、 950 m中段取多组岩芯, 结合地应力实测结果及岩石力学室内试验确定各中段岩石力学指标的取值. 研究以3个中段部分工程位置为例进行岩爆类型预测, 具体岩爆类型评价指标见表8.
将山西紫金3个中段部分区域的评价指标数据(表7)作为模型的输入, 得到模型预测结果如表8所示.

表7 890 m中段岩爆类型评价指标Tab.7 Prediction indicators for rockburst typesat 890 m level

表8 各中段部分巷道岩爆类型预测结果Tab.8 Prediction results of rock burst typesat various levels
从表8可看出, 830 m石门、 890 m中段沿脉运输巷道与950 m阶段运输巷与穿脉交界处, 斑岩型金矿的岩爆倾向性基本为“无岩爆”和“弱岩爆”类别, 在该区域开采时基本不可能发生强烈岩爆. 预测结果与现场的观测结果一致, 以上中段的各类井巷工程完整性较好, 未发现明显的片帮、 冒顶等现象.
4 结语
1) 结合397组岩爆工程案例, 利用KNN、 SVM与决策树模型进行岩爆类型预测, 结果表明主成分分析预处理对预测准确率并无改善, 采用过采样SMOTE算法仅对决策树模型有明显的提升, 故使用采用SMOTE算法预处理的SMOTE-DT模型及仅对原始数据集进行标准化处理的KNN、 SVM模型, 3种模型的预测准确率分别为68.75%、 57.50%与77.50%, 表明3种算法均能通过原始数据集进行有效训练.
2) SMOTE-DT与KNN模型低估岩爆类型的次数明显低于SVM模型, 模型预测更加安全保守, 且SMOTE-DT出现高估岩爆类型的情况较其他两种模型少, 预测准确性与安全保障性均优于KNN与SVM模型. 同时, SMOTE-DT模型对于4种岩爆类型的F1值均大于0.7, 分类性能稳定可靠, 而SVM模型在强岩爆类型的召回率低于50%, 因此首选SMOTE-DT模型作为岩爆预测模型.
3) 基于本文构建的KNN、 SVM与SMOTE-DT岩爆类型预测模型, 分析了山西紫金金矿830 m石门、 890 m中段沿脉运输巷道与950 m阶段运输巷与穿脉交界处的岩爆类型, 模型预测结果与现场实际观测情况相一致, 进一步验证了预测模型的可靠性.

