基于空间模糊C均值聚类和贝叶斯网络的抗噪声遥感图像变化检测

王子浩, 李轶鲲,2,3, 李小军,2,3, 杨树文,2,3

(1.兰州交通大学测绘与地理信息学院,兰州 730070; 2.地理国情监测技术应用国家地方联合工程研究中心,兰州 730070; 3.甘肃省地理国情监测工程实验室,兰州 730070)

0 引言

遥感图像变化检测是通过观察不同时相遥感图像中的地物以识别其状态变化的过程[1-2]。目前,遥感变化检测技术面临的最大挑战是遥感图像中光谱信息的复杂性,而当图像复杂性伴随常见噪声干扰时,往往会降低变化检测精度[3]。

传统的变化检测方法主要分为分类后比较法(post classification comparison,PCC)和变化向量分析法(change vector analysis,CVA)[4]2类。其中PCC是将2幅不同时相遥感图像进行分类,然后根据分类图识别变化信息,但是PCC法易受累计分类误差的影响。而CVA是基于不同时相遥感图像的差异图像进行变化检测,因而易受不同大气条件、太阳角度、土壤湿度、植被物候等干扰因素影响,对图像辐射校正的要求极其严格,特别不适应用于当今光谱信息复杂的遥感图像[5-7]。为此,Chen等[8]提出后验概率空间向量变化分析法(change vector analysis in posterior probability space,CVAPS)。该方法克服了PCC的缺点,放宽了CVA对遥感图像辐射校正的严格要求,具有更高的变化检测性能。CVAPS使用支持向量机(support vector machine,SVM)估计遥感图像像素的后验概率向量,但是SVM易受遥感图像“同物易谱”、“异物同谱”、混合像元及图像噪声的不利影响,往往不能准确地估计复杂像元的后验概率向量。为此,李轶鲲等[9]提出了基于模糊C均值聚类(fuzzy C-means clustering, FCM)和简单贝叶斯网络(simple Bayesian network, SBN)的后验概率向量变化分析法 (FCM-SBN-CVAPS)。该方法通过建立像素与多种地物的随机链接,能够有效处理“同物易谱”、“异物同谱”及混合像元等问题。然而,当遥感图像被高斯噪声、椒盐噪声或混合噪声污染时,该算法中的FCM对噪声较为敏感,其模糊隶属度的估计精度会受到噪声影响而下降,进而影响SBN估计后验概率向量的精度[10-12]。

为解决FCM易受噪声影响的问题,Ahmed等[13]提出一种基于空间约束的模糊C均值聚类(fuzzy C-means clustering with spatial constraints,FCM_S)算法。在此基础上,Chen等[14]进一步提出一种基于空间约束的核距离模糊C均值聚类(the kernel fuzzy C-means with spatial constraints,KFCM_S)算法。FCM_S和KFCM_S通过滤波和邻域权重来引入空间信息,增强了FCM对噪声的鲁棒性。然而,FCM_S和KFCM_S的运算量较大,为了提高效率,研究人员基于中值和均值滤波提出了简化邻域项的模糊聚类算法,如FCM_S1,FCM_S2,KFCM_S1和KFCM_S2。但是以上算法均有邻域参数引入,为避免参数引入并提高算法对不同噪声的自适应能力,Krinidis等[15]通过引入空间模糊因子提出了基于模糊局部信息C均值聚类 (fuzzy local information C-means,FLICM) 算法。

由于以上5种空间FCM算法能够较好地分解受高斯、椒盐和混合噪声污染的遥感图像中的混合像元。因此,本文在CVAPS框架下,在Yang等[16]工作的基础上,将FCM_S1,FCM_S2,KFCM_S1,KFCM_S2和FLICM与SBN相结合,提出了FCM_S1-SBN-CVAPS,FCM_S2-SBN-CVAPS,KFCM_S1-SBN-CVAPS,KFCM_S2-SBN-CVAPS和FLICM-SBN-CVAPS这5种改进的变化检测算法,以验证所提出的5种算法分别针对高斯、椒盐和混合噪声的鲁棒性。

1 FCM-SBN-CVAPS基本原理

1.1 FCM聚类算法

FCM通过建立像素与信号类间一对多的关系,实现了混合像元的分解。其中,信号类为图像中具有类似光谱特点的像素所组成的聚类。FCM会自动建立多个信号类,采用像素距各个信号类中心的距离差值平方最小的原则,对隶属度集合U={u1,u2,…,un}和n个信号类中心V={v1,v2,…,vn}不断迭代,得到单一像素中对每一个信号类的隶属度。FCM算法的目标函数为:

(1)

式中:pi,j为图像中第i行第j列的像素;vk为第k个信号类中心;n为信号类数量;uk(i,j)为pi,j属于第k个信号类的隶属度;q为控制FCM聚类模糊度的参数。

1.2 SBN构建

如图1所示,SBN基于像素与信号类和信号类与地物的随机链接P(ωk|pi,j)及P(Lv|ωk),计算得到像素属于不同地物的后验概率,其计算公式为:

(2)

图1 SBN结构

式中:P(ωk|pi,j)可以通过模糊隶属度uk(i,j)估计得到;P(Lv|ωk)可以通过专家提供的训练样本估计得到,具体的估计方法参考文献[9]。

1.3 CVAPS法

假设一个像元在t1时相属于荒地和植被的概率分别为49%和51%,在t2时相属于荒地和植被的概率分别为51%和49%。如果通过最大后验概率准则(maximum a posteriori,MAP)进行分类,该像元在t1时相为植被,在t2时相为荒地。在PCC方法下,该像元会被判断为变化像元。然而该像元光谱信息及后验概率向量仅发生了轻微变化,却被误判为变化像元,从而导致了过高的变化像元误检率。为了解决这一问题,CVAPS根据像元的后验概率变化强度来识别变化像元,原理如下:

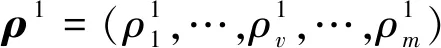
Δρ=ρ1-ρ2

。

(3)

相应地,像素pi,j在后验概率向量空间的变化强度为:

,

(4)

根据式(4)可得到后验概率空间变化强度图,再通过自动阈值算法,最终得到变化二值图[17]。

2 基于空间邻域信息的FCM算法

2.1 算法框架

由于FCM-SBN-CVAPS算法中的FCM算法在聚类过程中忽略了空间信息,因而在噪声影响下其估计的模糊隶属度矩阵不够准确,从而影响后续变化检测的精度[18-19]。对于这个问题,本文采用5种不同的基于空间邻域信息的FCM以提高CVAPS模型的抗噪能力。如图2的算法流程框图所示,本文涉及到基于空间邻域信息的FCM算法包括: FCM_S1-SBN-CVAPS,FCM_S2-SBN-CVAPS,KFCM_S1-SBN-CVAPS,KFCM_S2-SBN-CVAPS和FLICM-SBN-CVAPS。

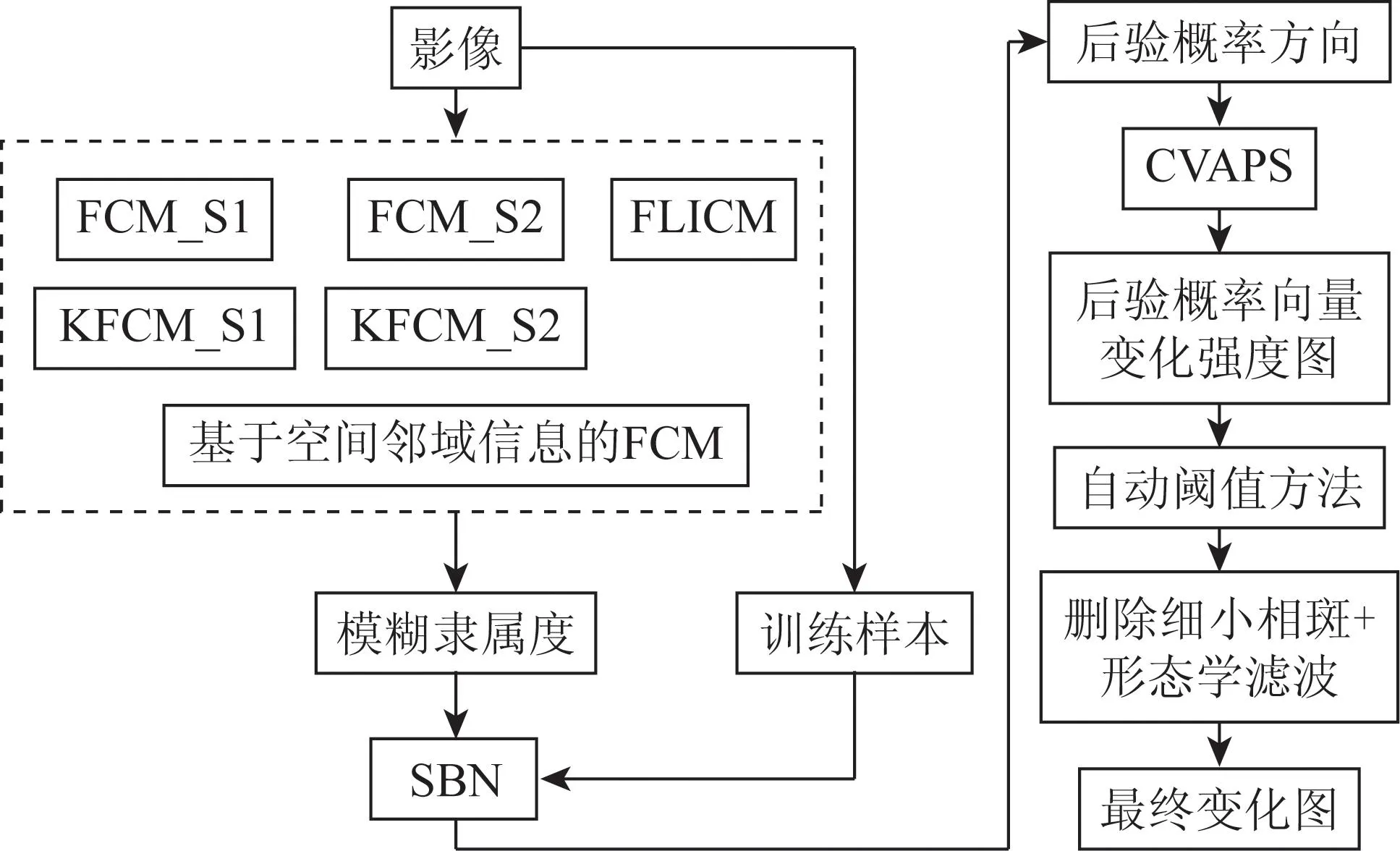
图2 算法流程图

2.2 简化邻域项的模糊聚类算法

FCM_S算法通过计算邻域像素和中心像素光谱特征的欧氏距离来修正中心像素的模糊隶属度,从而引入了空间领域信息,增强了FCM的抗噪性,但其计算量过大,因此本文采用FCM_S1算法和FCM_S2算法。FCM_S1算法和FCM_S2算法首先对图像进行均值和中值滤波,然后基于滤波结果和与邻域像素光谱特征的欧氏距离迭代计算中心像素的隶属度矩阵。因为使用了均值和中值滤波,FCM_S1和FCM_S2算法分别对高斯噪声和椒盐噪声有较高的鲁棒性。FCM_S1和FCM_S2的目标函数J1和J2分别为:

,

(5)

,

(6)

2.3 KFCM_S算法

KFCM_S算法运用了高斯核函数的距离测度来替换FCM中的欧氏距离,可以将低维空间中的非线性变量转换为高维空间的简单线性变量,减少邻域空间上噪声和异常值对计算隶属度矩阵的影响,使其计算隶属度矩阵时更加稳健。KFCM_S1和KFCM_S2算法在KFCM算法的基础上,基于图像中值和均值滤波结果,进行迭代计算。图像滤波增强了KFCM_S1算法和KFCM_S2算法对椒盐噪声和高斯噪声的抗噪性,也减少了算法的运行时间。KFCM_S1和KFCM_S2的目标函数J3和J4为:

,

(7)

,

(8)

式中K(·)为核距离,本文中K(·)为高斯径向基函数(Gaussian radial basis function,GRBF)。

2.4 FLICM算法

FLICM算法使用了一种模糊局部空间信息和光谱信息相似性的距离测度,保证了算法的抗噪性能,而且保留了图像细节。由于该算法通过局部空间的模糊约束因子自动约束了图像细节和噪声的平衡,可以不需要噪声的先验知识,从而自适应处理不同噪声。FLICM的目标函数J5为:

(9)

式中Gijk为空间模糊因子。

FLICM算法通过引入Gijk,避免人工调整参数因子,提高了算法对不同噪声的自适应性。

3 实验

论文实现了5种变化检测模型(FCM_S1-SBN-CVAPS,FCM_S2-SBN-CVAPS,KFCM_S1-SBN-CVAPS,KFCM_S2-SBN-CVAPS和FLICM -SBN-CVAPS),将论文提出的变化检测方法和SVM-CVAPS[8]和FCM-SBN-CVAPS[9]算法进行了对比,对研究区图像进行变化检测。变化检测实验针对7种变化检测算法的抗噪性,从4个方面展开: ①变化检测算法对高斯、椒盐和混合噪声的抗噪性分析; ②噪声敏感度分析; ③模糊度和训练样本数敏感度分析; ④运行时间分析。

3.1 研究区数据

本文实验图像为2017年和2019年的2幅600像元×600像元7波段Landsat8图像,均进行了辐射定标和大气校正等预处理。图像主要包含4种地物类型,分别为建筑物、山地、农地和荒地,如图3(a)和(b)所示。图3(c)为基于人工标识的变化区域图像二值图。

(a) 2017年 (b) 2019年 (c) 人工检测的变化结果

3.2 综合性能比较

为了验证算法的抗噪性能,本文设计了3类噪声实验: ①5%椒盐噪声; ②零均值,方差0.01的高斯噪声; ③混合噪声(0.5%椒盐噪声+零均值,方差0.001的高斯噪声)。其中,信号类数(聚类数)为10,模糊度q为3.5,训练样本为1 000,自动阈值算法为大津法。

图4为添加5%椒盐噪声的研究区图像及SVM-CVAPS,FCM-SBN-CVAPS,FCM_S2-SBN-CVAPS和KFCM_S2-SBN-CVAPS算法的变化二值图,检测精度见表1。如图4和表1所示,在5%椒盐噪声影响下,SVM-CVAPS和FCM-SBN-CVAPS算法存在大量的误检区域,其变化检测Kappa系数分别为0.406和0.647。而FCM_S2-SBN-CVAPS和KFCM_S2-SBN-CVAPS算法的误检区域大大减少,其变化检测Kappa值分别为0.844和0.751。其中,KFCM_S2-SBN-CVAPS算法出现了部分的误检区域,导致其变化检测精度低于FCM_S2-SBN-CVAPS算法。从表1中可以发现,当添加5%椒盐噪声时,FCM_S2-SBN-CVAPS性能最优。其中,FCM_S2-SBN-CVAPS算法的错检率和漏检率比FCM-SBN-CVAPS算法低0.132和0.126,总体精度和Kappa系数比FCM-SBN-CVAPS算法高0.022和0.197,证明FCM_S2-SBN-CVAPS算法较为适合处理椒盐噪声。

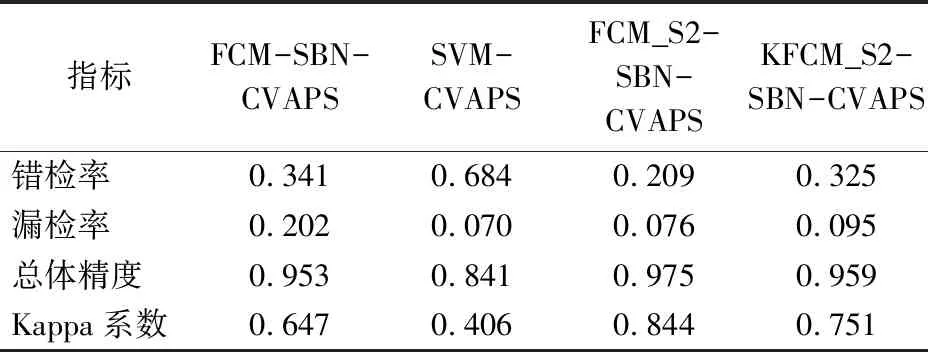
表1 变化检测模型性能比较(5%椒盐噪声)

(a) 2017年Landsat8影像 (b) 2019年Landsat8影像 (c) SVM-CVAPS

图5为添加零均值,方差0.01高斯噪声的研究区图像及采用SVM-CVAPS,FCM_SBN-CVAPS,FCM_S1-SBN-CVAPS和KFCM_S1-SBN-CVAPS算法的变化二值图,检测精度见表2。其中,SVM-CVAPS和FCM-SBN-CVAPS算法存在很多漏检和误检区域,其变化检测Kappa系数分别为0.466和0.497。与此相比,FCM_S1-SBN-CVAPS和KFCM_S1-SBN-CVAPS算法精度更高,Kappa分别为0.798和0.830。从表2中可以发现,当添加零均值,方差0.01的高斯噪声时,FCM_S1-SBN-CVAPS和KFCM_S1-SBN-CVAPS均取得较好的检测结果,但KFCM_S1-SBN-CVAPS的性能略高于FCM_S1-SBN-CVAPS。另外,KFCM_S1-SBN-CVAPS算法的错检率和漏检率比FCM-SBN-CVAPS算法低0.431和0.284,总体精度和Kappa系数比FCM-SBN-CVAPS算法高0.054和0.333,证明由于使用GRBF函数为核距离,KFCM_S1-SBN-CVAPS算法较为适合处理较弱的高斯噪声。

表2 变化检测模型性能比较(零均值,方差0.01高斯噪声)

图6为添加混合噪声(0.5%椒盐噪声和零均值,方差0.001高斯噪声)的图像和使用SVM-CVAPS,FCM-SBN-CVAPS和FLICM-SBN-CVAPS算法的变化二值图如图6(c)—(e)所示,检测精度见表3。从图中可以看出,SVM-CVAPS和FCM-SBN-CVAPS算法,受混合噪声影响,过度估计变化像元,其误检现象较为严重。另外,SVM-CVAPS检测到的变化区有很多漏检孔洞,检测精度最低。FLICM-SBN-CVAPS算法没有明显误检区域,但漏检情况较为严重,但总体检测效果最好。从表3中可以发现,当同时添加0.5%椒盐噪声和零均值,方差0.001高斯噪声时,由于FLICM-SBN-CVAPS算法可以自适应地处理混合噪音,因而取得了最高的检测精度: 其Kappa系数为0.851,比SVM-CVAPS和FCM-SBN-CVAPS分别高0.302和0.100; 其总体精度为0.979,比SVM-CVAPS和FCM-SBN-CVAPS分别高0.081和0.022。

表3 变化检测模型性能比较(0.5%椒盐噪声+零均值,方差0.001的高斯噪声)

(a) 2017年Landsat8影像 (b) 2019年Landsat8影像 (c) SVM-CVAPS

3.3 噪声鲁棒性

为分析上述算法的抗噪性能,本文对SVM-CVAPS与FCM-SBN-CVAPS这2种传统算法,和FCM_S1-SBN-CVAPS,FCM_S2-SBN-CVAPS,KFCM_S1-SBN-CVAPS和KFCM_S2-SBN-CVAPS这4种改进算法进行噪声敏感度分析。实验对研究区图像添加不同强度的高斯噪声和椒盐噪声。4种改进算法分别对受椒盐噪声(5%,6%,7%和8%)和高斯噪声(零均值,方差分别为0.005,0.010,0.015和0.020)污染的图像进行噪声敏感度分析。其中,本文通过实验确定最佳的滤波窗口大小为3×3,滤波权重系数为0.5,模糊度q统一设置为3.5。

图7中展示了4种改进算法处理受不同程度椒盐和高斯噪声污染图像的Kappa系数。如图7(a)所示,FCM_S2-SBN-CVAPS对受椒盐噪声污染图像进行变化检测的Kappa系数值最高,证明其对椒盐噪声的鲁棒性较好。从图7(b)中可以发现,FCM_S1-SBN-CVAPS 和KFCM_S1-SBN-CVAPS在处理受高斯噪声污染图像时,其Kappa系数值较高,证明2种算法对高斯噪声的鲁棒性较好。值得注意的是,KFCM_S1-SBN-CVAPS算法在高斯噪声较大时无法取得满意的变化检测精度。

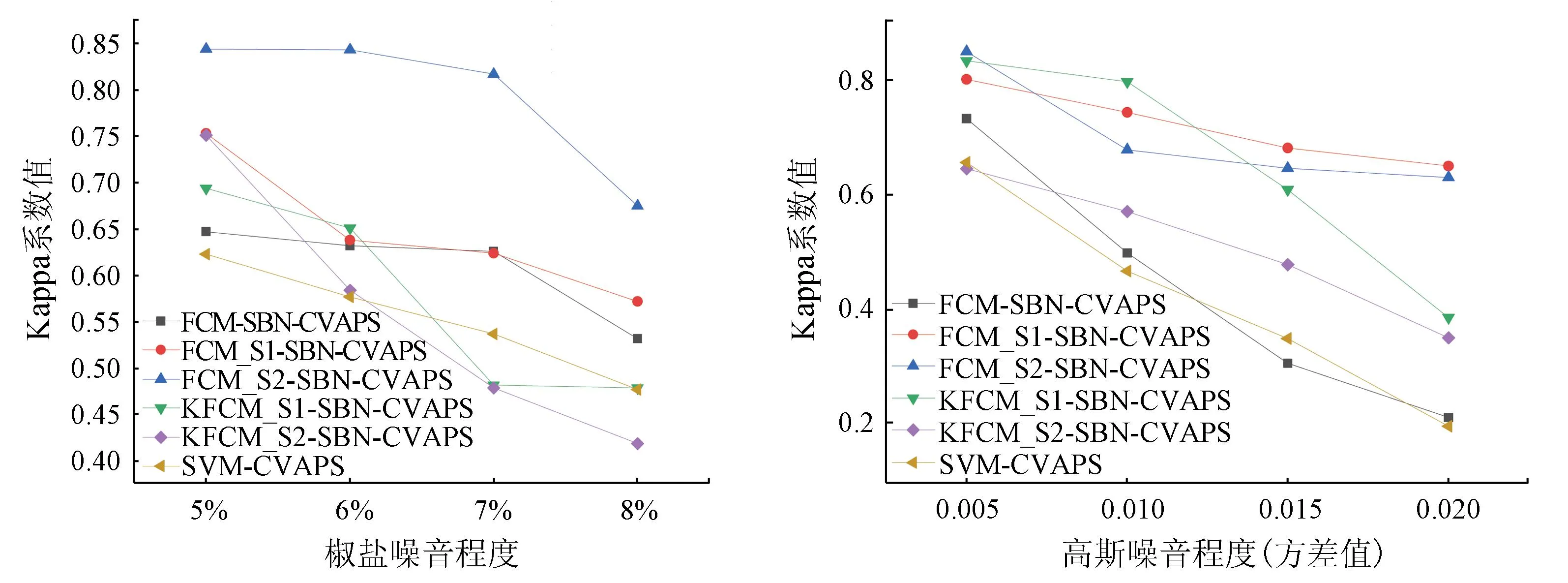
(a) 椒盐噪声 (b) 高斯噪声

另外,与FCM_S1-SBN-CVAPS和FCM_S2-SBN-CVAPS算法相比,KFCM_S1-SBN-CVAPS和KFCM_S2-SBN-CVAPS算法Kappa系数较低,其将一些错检区域和正确区域连在一起。特别是当在高斯噪声的零均值,方差为0.020时,KFCM_S1-SBN-CVAPS算法Kappa值仅为0.385,其检测到的变化区域因高斯噪声影响变成散布全图像的细小像斑。由此看出,KFCM_S1-SBN-CVAPS无法有效抵抗较强高斯噪声的影响。

由于FLICM算法需要人工设定的参数较少,且可以自适应不同类型的噪声,因此本实验针对FLICM-SBN-CVAPS算法,分别添加了单一噪声(椒盐噪声0.4%、椒盐噪声0.6%和零均值,方差为0.001的高斯噪声)和混合噪声(零均值,方差0.001的高斯噪声+0.2%/0.4%/0.6%椒盐噪声)的遥感图像进行变化检测和抗噪性能分析。从表4可知,当噪声信号较弱时,FLICM-SBN-CVAPS算法比FCM-SBN-CVAPS算法抗噪性更强,可以较好地处理受单一噪声和混合噪声污染的图像,取得了较高的Kappa值。在零均值,方差0.001的高斯噪声影响下,FLICM-SBN-CVAPS算法比FCM-SBN-CVAPS和SVM-CVAPS算法的Kappa值分别高0.352和0.257,在混合噪声(零均值,方差0.001的高斯噪声+椒盐噪声0.2%)影响下,FLICM-SBN-CVAPS算法比FCM-SBN-CVAPS和SVM-CVAPS算法的Kappa值分别高0.094和0.186。然而,当噪声污染严重时,FLICM-SBN-CVAPS的检测精度较低。

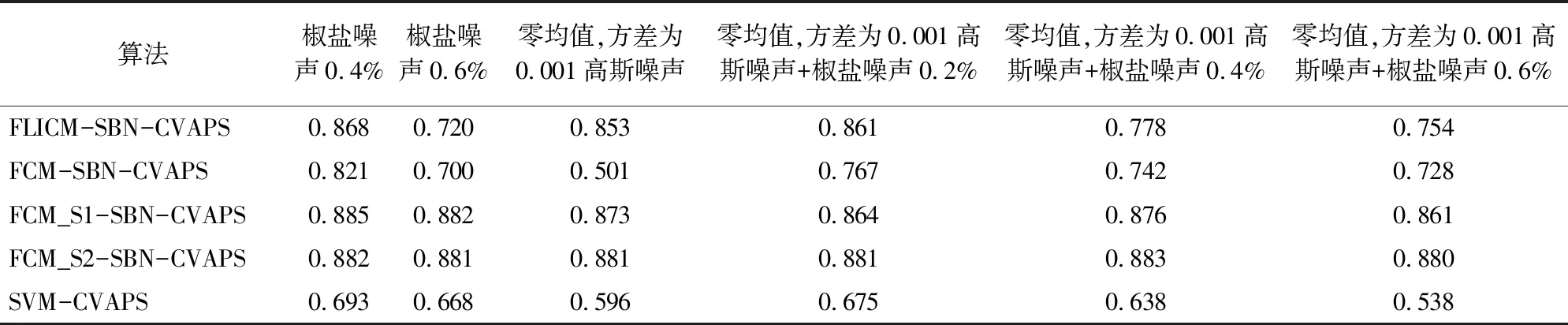
表4 FLICM-SBN-CVAPS的噪声敏感度表(Kappa系数值)

在表4中,FCM_S1-SBN-CVAPS算法和FCM_S2-SBN-CVAPS算法Kappa值均为0.86以上,比如在零均值,方差0.001的高斯噪声和椒盐噪声0.2%影响下,FCM_S1-SBN-CVAPS算法和FCM_S2-SBN-CVAPS算法Kappa值分别为0.864和0.881。由此证明FCM_S1-SBN-CVAPS和FCM_S2-SBN-CVAPS算法可以克服较小程度的混合噪声污染。

3.4 模糊度和训练样本数量敏感度

本节实验比较了不同的模糊度和训练样本数量对FCM_S1-SBN-CVAPS,FCM_S2-SBN-CVAPS,KFCM_S1-SBN-CVAPS和KFCM_S2-SBN-CVAPS变化检测算法抗噪性能的影响。在变化检测过程中,分别设定不同的模糊度q(1.0,1.5,2.0,2.5,3.0,3.5,4.0和4.5)和不同的训练样本数量(1 000,2 000,3 000,4 000和5 000)(图8和图9)。其中FCM_S1-SBN-CVAPS和KFCM_S1-SBN-CVAPS处理添加零均值,方差0.010高斯噪声的图像,FCM_S2-SBN-CVAPS和KFCM_S2-SBN-CVAPS处理添加5%椒盐噪声的图像。

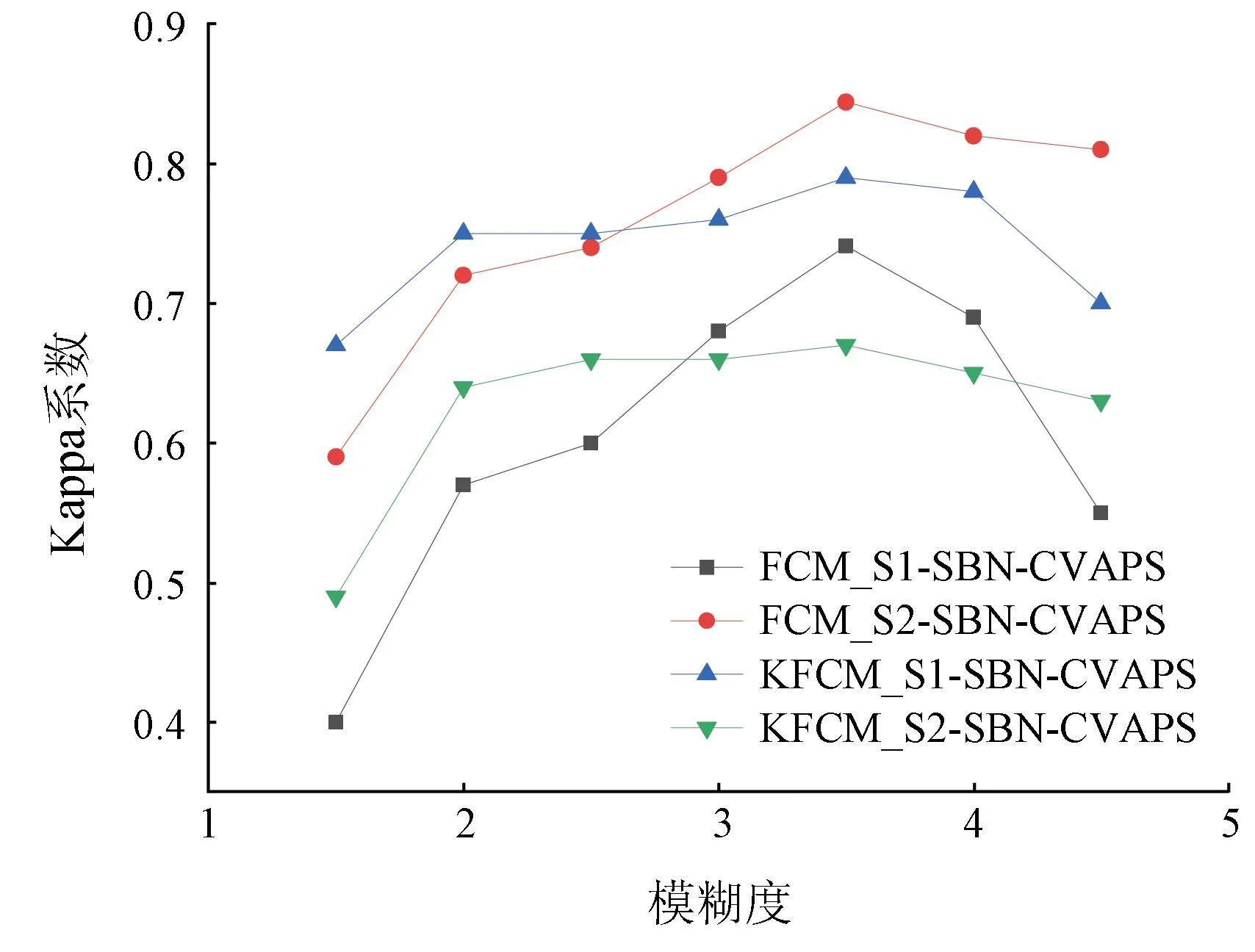
图8 模糊度敏感度图

图9 训练样本数量敏感度图

由图8可以观察到,当模糊度q为1.5时,4种算法的Kappa系数值均偏低。这是由于,模糊度过低的FCM改进算法无法有效分解图像中的混合像元,导致其变化检测效果较差。当模糊度q为3.5时,4种变化检测算法均取得最高Kappa系数值。由此看出,当模糊度为3.5时,算法精度较为理想。

图9所示,在训练样本数分别为1 000,2 000,3 000,4 000和5 000时,所有算法的Kappa系数值变化幅度均较小,最大差异仅为0.04(KFCM_S1-SBN-CVAPS算法)。从而证明训练样本数量的变化对这4种算法变化检测的影响较小。说明当训练样本数量较少时,这4种算法依然可以得到较好的变化检测结果。

3.5 算法运算时间

本节测试了所涉及算法的运行时间。实验发现,所涉及算法模型中模糊聚类部分运算耗时最长。当处理5%椒盐噪声的遥感图像时, FCM_S1,FCM_S2与FCM的算法运行时间分别为48 s和44 s,差值不大于5 s。而KFCM_S1,KFCM_S2和FLICM的算法运行时间较长,运行时间分别为67 s,65 s和61 s。由于KFCM_S1和KFCM_S2的核距离运算量较大,从而延长了其总运行时间。

4 结论

本文针对FCM-SBN-CVAPS变化检测模型的FCM部分进行了改进,在CVAPS框架下引入了基于空间邻域信息的5种FCM算法(FCM_S1, FCM_S2, KFCM_S1, KFCM_S2, FLICM)。由于5种FCM算法在高斯、椒盐和混合噪声污染条件下,能够有效分解混合像元,从而提高了相应变化检测算法的抗噪声能力,使得最终变化检测结果不易受噪声的影响。

但是由于KFCM_S1-SBN-CVAPS和KFCM_S2-SBN-CVAPS方法中要对核距离进行计算,若对所有核距离计算,会导致计算复杂度过大。因此,结合核距离的约束与优化是课题组的下一步工作。