质量引导下的最小二乘相位解缠算法
肖晖, 李惠堂, 顾约翰, 盛庆红
(1.南京航空航天大学航天学院,南京 210016; 2.南京晓庄学院环境科学学院,南京 211171)
0 引言
干涉合成孔径雷达(interferometric synthetic aperture Radar,InSAR[1])是利用2幅或多幅相干合成孔径雷达(synthetic aperture Radar,SAR)图像复数数据得到干涉相位,并通过成像几何模型建立相位与地形信息之间的对应关系,从而获取地表三维信息[2]和形变信息的对地观测技术[3-4]。由于InSAR使用的SAR图像为复数数据,所以在干涉处理时获得的干涉相位因三角函数的周期性被缠绕在(-π,π]之间,导致缠绕相位与绝对相位之间存在2kπ的差异[5],所以需要通过相位解缠来恢复相位主值中被模糊掉的整周相位,从而求解地形高程对应的绝对相位。
目前常见的相位解缠方法主要包括3类[6]: 基于路径跟踪、基于最小范数和基于网络规划的相位解缠算法。基于路径跟踪的相位解缠算法通过先验信息制定合适的积分路径,对相邻像元进行积分,实现相位解缠,代表算法有枝切法和质量引导法。基于路径跟踪的相位解缠算法具有解缠速度快、效率高等优点,但由于积分路径难以确定,算法精度无法保证[7-9]。基于最小范数的相位解缠方法是将解缠问题转换为缠绕相位与解缠相位差异最小化的数学问题,利用相位的离散偏导数作为最小范数参量实现相位解缠,代表算法有无权最小二乘法[10-11]和加权最小二乘法[12-13]。基于网络规划的相位解缠算法通过网络流理念将解缠相位和缠绕相位之间的离散偏导数之差最小化,从而获取全局最优解,代表算法有基于最小费用流相位解缠算法和基于不规则网络的相位解缠算法[14]。此类方法大大提高了相位解缠的运行效率和解缠精度,但如何确定适当的权重矩阵,从而获取更好的积分路径仍然是研究的重点和难点[15-16]。
针对复杂山区中因斜视成像和地形带来的相位失真及相位噪声,本文提出质量引导与最小二乘相结合的相位解缠算法,首先根据干涉相位质量高低在高质量区域利用质量引导法获取可靠的解缠结果,然后利用最小二乘法的平滑作用,在低质量区域进行最小二乘法相位解缠,提高低质量区域解缠的连续性,从而获得全局最优的解缠结果。仿真数据与真实数据结果表明该算法很好地克服了质量引导法无法阻止相位解缠误差扩散的问题,还可以在最小二乘法的平滑作用下,提高低质量区域解缠的连续性,避免了低质量像元因相位误差在路径积分中堆积,导致与高质量像元解缠结果间出现相位跳变的现象。
1 数据源
1.1 模拟数据
为了尽可能模拟复杂山区地形,本文采用Peaks函数生成255×255的模拟数字高程模型(digital elevation model,DEM)矩阵,如图1(a)所示,高程分布在0~63 m,其中包含3个山峰和2个山谷区域。图1(b)是根据图1(a)得到的真实相位图,其相位值处在[-34,42] rad,均值为2.622 rad。由于山区中植物茂盛,所以对应的时间及空间相干性较低。为了更逼近真实数据,对模拟DEM生成的干涉相位添加最大值为0.65 rad的随机噪声。图1(c)为在真实相位加入随机噪声后缠绕在(-π,π]的干涉相位图,从图1中可以看出在黑色框选区域因噪声影响缠绕相位出现大量不一致情况。
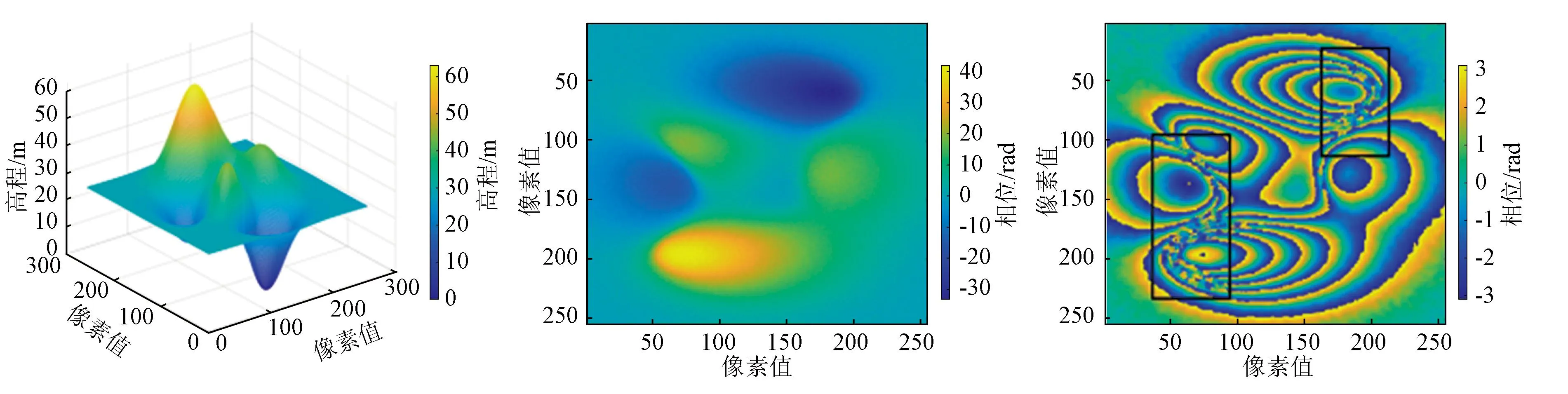
(a) DEM 3D视图 (b) DEM平面视图 (c) 缠绕相位
1.2 真实数据
为了验证本文提出的相位解缠算法在真实数据中的有效性,采用位于中国陕西西安的秦岭山脉作为研究区域,该区域中心经纬度为E108°50′,N33°35′,相关数据如图2所示。图2(b)给出研究区域的SRTM-1拼接后的影像,可以看出该区域群山连绵、地形复杂,经过对该区域SRTM DEM进行统计,可知高程分布在200~3 000 m。

(a) 研究区SRTM-1影像图 (b) 研究区高程
采用的真实干涉SAR影像对为Sentinel-1A数据, 产品类型为SLC,成像模式为IW,入射角为39.08°,轨道方向为升轨。获取2019年11月26日和12月 8 日的InSAR干涉影像对,影像大小为1 000像素×1 000像素,时间基线为12 d,空间基线为24.89 m。
在获取SAR干涉影像对后,需要对获取的图像进行InSAR流程化处理,处理过程如图3所示,可以看出该研究区域基于SAR干涉影像对生成的干涉相位图纹理模糊,经过干涉图滤波后出现部分干涉条纹,经过去平地效应后干涉条纹较明显,结合该区域的SRTM DEM影像可以看出在山谷区域有较连续的干涉条纹,而在山峰处干涉相位杂乱无章。

图3 干涉影像对流程化处理
在经过流程化处理后的干涉相位图中选取其中的1 000像素×1 000像素进行相位解缠研究,图4给出实验干涉相位相关数据,其中图4(a)为干涉相位数据,图4(b)为根据SLC影像对求解的相关系数图,图4(c)为干涉相位中的残差点分布图。通过图4可以看出,该实验区域除相关性较高区域有明显干涉条纹,其他区域相位杂乱无章。
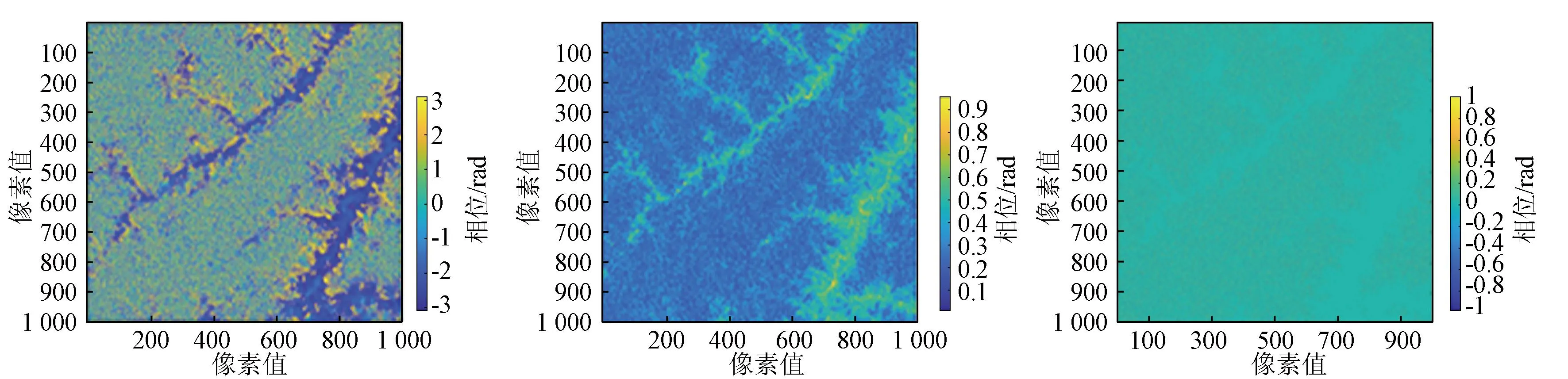
(a) 缠绕相位 (b) 相关系数 (c)残差点分布
由于SAR影像与SRTM DEM数据空间分辨率不同,所以利用选取的控制点,对SRTM DEM重采样,使2张影像在控制点相同的条件下具有相同的尺寸,从而保证相同的分辨率。图5给出研究区域对应的重采样后DEM数据及求解的相位导数方差图。通过图5(a)—(b)中DEM数据可以看出,实验区域高程分布在400~2 000 m之间,地形多变,主要包含2条山谷和3个山峰。图5(c)是根据缠绕相位获得的相位导数方差,从图中可以看出研究区域内山谷地区因地形相对平坦,植被较少导致相位导数方差较小,相位质量高。

(a) 秦岭地区DEM 3D视图 (b) DEM平面视图 (c) 相位导数方差
2 研究方法
质量引导法利用相位质量图作为辅助信息来布置积分路径[17]。相位质量图是从干涉影像对或干涉相位中提取、用来衡量干涉相位质量好坏的标准。常用的相位质量图主要有相关系数图、伪相关系数图、相位导数方差图和最大相位梯度图[18]。大量的实践证明,在无法获得相关系数图时,相位导数方差图是最可靠的质量图。本文重点介绍相位导数方差图的计算方法。
相位导数方差Zm,n是利用干涉相位局部统计特性,判断相位数据的好坏程度,其计算公式为:
(1)
,
(2)
,
(3)

相位导数方差图是利用k×k范围内相位导数求取的质量图,该质量图表征的是受到干扰后干涉相位的连续性,即相位导数越大对应的干涉相位连续性越差,可靠性越低。
为了减小残差点引起的全局误差,获取更精确的解缠相位值,加权最小二乘法通过引入质量图、掩模等先验信息,为干涉相位设置不同权重,尤其是对低相干区域赋予较低权重。通常情况,权重wi,j的取值范围在[0,1],可以由相位质量图或其他先验信息获得。引入权重后,最小化梯度差异问题演变成求解下式的最小值,公式为:
,
(4)
,
(5)
式中:W为最小值;ψ为绝对相位;wi,j为第i行、第j列的权值。
式(4)中最小二乘解ψi,j满足:
Ui,j(ψi+1,j-ψi,j)-Ui-1,j(ψi,j-ψi-1,j)+Vi,j(ψi,j+1-ψi,j)-Vi,j-1(ψi,j-ψi,j-1)=ci,j
,
(6)

(7)
式中ci,j为加权拉普拉斯算子。
由于引入权值后,无法直接采用傅里叶变换求解解缠相位,所以在实际运算中,常通过某种数学变换将缠绕相位和绝对相位之间的关系线性化,再采用傅里叶变换求解ψ的初始值,并进行迭代循环,从而求得解缠相位。
本文实现的质量引导与最小二乘相结合的相位解缠算法,其假设干涉相位是二维的连续函数,则只需要从r0开始沿着某一条路径C进行积分,可得到任意一点r的相位,即
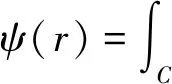
,
(8)
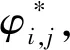
。
(9)
根据最小二乘相位解缠的基本思想,最终解缠相位ψi,j将满足如下要求,即
,
(10)
,
(11)
该算法主要步骤如下: ①根据干涉相位图计算相位导数方差图作为质量图; ②搜索相位导数方差图中质量最好的点,并由该点开始,根据质量引导法解缠步骤进行相位解缠工作; ③将相位导数方差数值归一化,代入式(5),计算加权最小二乘解缠算法中的权重; ④将质量引导法解缠结果作为新的干涉质量图,结合步骤③求解的权重,设置迭代次数,求解最终解缠结果。该算法的优势在于利用质量引导法在相位质量高的区域具有较高的解缠精确性,从而保证在进行加权最小二乘运算时,该区域的解缠相位依然具有较高的精确性,同时在全局算法的作用下,保证了高质量区域与相邻的低质量区域间的解缠相位连续性,从而获取具有更高精确性和一致性的解缠结果。
3 结果与分析
3.1 模拟数据实验结果
分别采用枝切法、基于相位导数方差图的质量引导法、无权最小二乘法、加权最小二乘法和本文提出的质量引导与最小二乘法相结合的相位解缠算法对模拟数据进行解缠处理。
图6给出实验中使用的干涉相位相关图像,其中图6(a)为根据图1(c)计算得到的残差点分布图,其中±1为残差点,0为非残差点; 图6(b)为枝切法中平衡残差点极性的枝切线布置图; 图6(c)为计算所得的图1(c)的相位导数方差图。根据图1(c)中干涉相位在黑色方框中的密集分布,结合图6,可以看出相位噪声使对应位置的残差点数量增多,导致该区域内枝切法为平衡残差点极性布置了大量的枝切线,同时相位噪声使该位置相位连续性降低,质量引导法使用的相位导数方差的数值增加,即该位置相位质量较差,对应的解缠次序也靠后。

(a) 残差点分布 (b) 枝切线分布 (c) 相位导数方差

(a) 枝切法解缠结果图 (b) 枝切法反缠绕图 (c) 枝切法解缠误差分布图
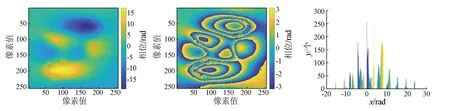
(g) 无权最小二乘法解缠结果图 (h) 无权最小二乘法反缠绕图 (i) 无权最小二乘法解缠误差分布图
图7给出各算法针对图1(c)干涉相位的解缠结果相关图,包括解缠结果、反缠绕和误差分布,表1给出根据解缠误差求解的均方根误差(root mean square error,RMSE)。图7(a) —(c)为枝切法解缠结果,其中出现因枝切线布置过于密集导致的无法解缠区域,在相位积分时由于缺乏该区域的积分相位值,导致在积分路径上的解缠相位整体小于邻近值,所相位误差集中在某几个范围内,其RMSE为7.37 rad。图7(d) —(f)为基于图6(c)的质量引导法解缠结果,其中相位误差在低质量区域中不断累积,导致解缠结果与周围高质量像元的解缠结果有明显相位跳变,相位误差分布较集中,其RMSE为2.37 rad。虽然枝切法和质量引导法因噪声区域误差较大,但在高质量数据区域有良好的解缠效果,同时反缠绕误差与原始干涉相位有较好一致性。基于最小范数算法的无权最小二乘法(图7(g) —(i))和加权最小二乘法(图7(j) —(l)),解缠结果表现出良好的相位连续性,但作为基于全局范围的解缠算法,使得相位误差全局平均化,导致反缠绕图与原始干涉相位吻合度不高,其RMSE分别为7.11 rad和4.07 rad。本文算法解缠结果(图7(m) —(o)),在结果上表现较理想,不仅保持了高质量相位的解缠精度,也平滑了高低质量像素间的相位跳变,通过误差分布可以看出,该方法将质量引导法中的集中相位误差平均化,很好地改善了整体相位的一致性,其RMSE为2.00 rad,结果表明该算法较其他算法在一致性和精确性上都有所提升。

表1 不同算法的解缠结果RMSE
3.2 真实数据实验结果
分别采用与模拟数据处理过程相同的相位解缠算法对真实数据进行处理,并分别给出解缠结果、反缠绕和解缠误差分布,如图8所示。通过对解缠误差进行统计,各算法RMSE如表2所示。由于山区内植物茂盛,获取的2幅干涉影像时间相关性很低; 地形起伏大降低了干涉影像的空间相关性,因此干涉相位中存在大量残差点,枝切线布置过于密集导致枝切法解缠失败。图8(a) —(c)为质量引导法解缠结果,从图8(a)可以看出解缠结果整体上符合地形趋势,其中1号黑色方框中的山峰区域和两侧的山谷区域与地形中对应位置相符,主要是由于山谷区域相关系数稍高,所以解缠结果在该区域具有良好的一致性。但图8(a)中的2号黑色方框中,结合图4(b)可以看出该区域没有干涉条纹且相关系数低,作为最后解缠的区域,路径积分中的误差积累使本应为山峰的区域被错误解缠为山谷。质量引导法的反缠绕结果图8(b)与原始相位图4(a)保持较高一致性,但因相位噪声较大,所以解缠结果误差图如图8(c)分布范围广,其RMSE为20.08 rad。图8(d) —(f)为无权最小二乘法解缠结果,从图8(d)可以看出仅在1号黑色方框的山谷区域与地形相符,在其他区域为了获取平滑的解缠结果使局部噪声全局传播,最终导致解缠相位偏离真实相位,无法辨识地形形状。该算法反缠绕后如图8(e)所示,与原始相位不符,其解缠结果误差分布(图8(f))较为集中,其RMSE为24.38 rad。图8(g) —(i)为加权最小二乘法解缠结果,由于该方法利用先验信息赋予权重,但由于先验信息也来自干涉相位数据,无法避免成像中的相位噪声,所以无法准确确定权重,仅在图8(g)中1号黑色方框中山谷处的解缠结果比无权最小二乘法理想,其他区域也是无法辨识地形,其RMSE为24.04 rad。图8(j) —(l)为本文算法解缠结果,通过图8(j)中1号和2号黑色方框中所示,2条地形坡度较小的山谷区域因具有很好的相干性,解缠结果具有很好的精确性和一致性,与地形也相吻合。图8(k)可以看出反缠绕结果与原始相位图4(a)高度一致。通过解缠结果误差分布图(图8(l))可以看出,误差较大的像素个数减少,误差分布也相对集中,通过统计得到RMSE为16.47 rad,较其他传统方法都低,表明解缠精度有所提升。

表2 真实数据各算法解缠结果RMSE统计

(a) 质量引导法解缠结果图 (b) 质量引导法反缠绕图 (c) 质量引导法解缠误差分布图
4 讨论与结论
为了提高InSAR在山区的DEM反演精度,本文针对山区严重的相位失相关和相位噪声问题,提出质量引导与最小二乘法相结合的相位解缠算法。首先利用质量引导法在高质量区域进行解缠,从而获取可靠的解缠结果。为了避免质量引导法在解缠过程中依赖于干涉相位的质量高低而出现高质量像元被优先解缠但低质量像元因相位误差在路径积分中堆积,导致与高质量像元解缠结果间出现相位跳变的现象,根据最小二乘法原理,基于解缠相位和缠绕相位之差的平方和最小准则,使缠绕相位离散偏导数和真实相位离散偏导数之差的平方和最小化,以质量引导法解缠结果作为缠绕相位进行最小二乘法相位解缠。实验结果表明,本文方法不仅可以保证质量引导法获得的高质量区域解缠相位的精确性,还可以在最小二乘法的平滑作用下,有效地避免低质量区域误差的传播,提高山区低质量区域解缠结果的一致性和精确性。

