大跨度空间结构预应力拉索索力测试研究*

邓德员, 邹锦华, 郑耀华, 戴 维

(1 中建钢构工程有限公司，深圳 518118；2 广东工业大学土木与交通工程学院，广州 510006；3 中建科工集团有限公司，深圳 518000)

0 引言

近年来,预应力体系被广泛应用于建筑结构中。预应力技术应用于大跨度空间结构,不仅可以提高结构刚度、减小结构挠度,还可以改善结构内力分布,从而达到降低材料用量和降低建设成本的目的。预应力拉索作为大跨度空间结构的关键受力构件,刚度小,基频较低[1],并且在运营期受极端天气及人为振动影响易发生拉索受损、拉杆失效、支座损坏等情况,对结构整体承载力影响较大[2-5]。拉索索力是评估大跨度空间结构工作状态的重要依据,因此,准确测量使用阶段大跨度空间结构拉索的索力,是保证大跨度空间结构安全和稳定的关键。

拉索性能是否满足使用要求取决于拉索现存索力的大小。徐郁峰等[6]介绍了频率法测量索力的原理,运用频率法对广州大学城中心区体育馆进行索力测试,并对测量结果进行了分析和讨论;Ricciardi等[7]在考虑拉索弯曲刚度和垂度的前提下运用数值迭代法,结合拉索振动模型,提出了新的索力计算公式,并在墨西拿海峡大桥主缆进行验证;Park K S等[8]考虑到抗弯刚度对索力计算的影响,运用有限元模型进行索力识别,通过实例对该方法进行验证;吴霄等[9]引入多尺度法求解考虑拉索垂度及抗弯刚度的拉索非线性振动问题;何雄君等[10]通过竣工时索力推求等效索长,结合有限元模拟进行索力测量,并指出使用HDPE套管对索力计算有一定影响。在特定的工程条件下,利用测试和拉索振动方程计算索力满足要求,但在长期运营下拉索参数会削弱。为了获得更准确的索力值,有必要对拉索参数进行识别。Kim等[11]提出了基于频率灵敏度修正的参数识别方法,可以同时对拉索索力、抗弯刚度等多个参数进行识别;Roman等[12]在拉索实测中发现拉索高阶频率比理想张拉弦偏高的现象,提出了相应的公式识别拉索的索力和抗弯刚度;Taehyo Park等[13]提出一种针对悬索桥常用的骑跨式连接双吊杆的参数识别办法,这种方法可以同时对索力、抗弯刚度、抗拉刚度等参数识别;李国强等[14]运用有限单元法与系统参数识别技术相结合的方法识别拉索索力和抗弯刚度;晏班夫等[15]利用动力刚度法和粒子群算法对带有中间支撑的拉索进行参数识别,结果表明该方法能较好改善索力识别精度。上述研究主要针对拉索在施工过程及新建结构或实验室较理想状态下的计算,并未考虑长期运营情况下拉索的预应力损失。

为准确获取运营期大跨度空间结构的拉索索力,本文提出一个基于有限元计算模型和利用现场实测频率进行参数识别的索力迭代修正的计算方法。该方法仅需已知设计参数,通过建立有限元模型,利用计算振型与实测频率联立能量法方程建立线性关系,即可求解修正参数及计算索力值;最后,对某体育馆预应力拉索进行一系列实测及计算验证。该方法能丰富大跨度空间结构预应力拉索索力的计算理论。

1 索力测试原理及计算方法

1.1 索振动基本方程

大跨度空间钢结构中预应力拉索截面一般较小,其自由振动可以视为按弦振动理论进行[16],计算模型如图1所示。

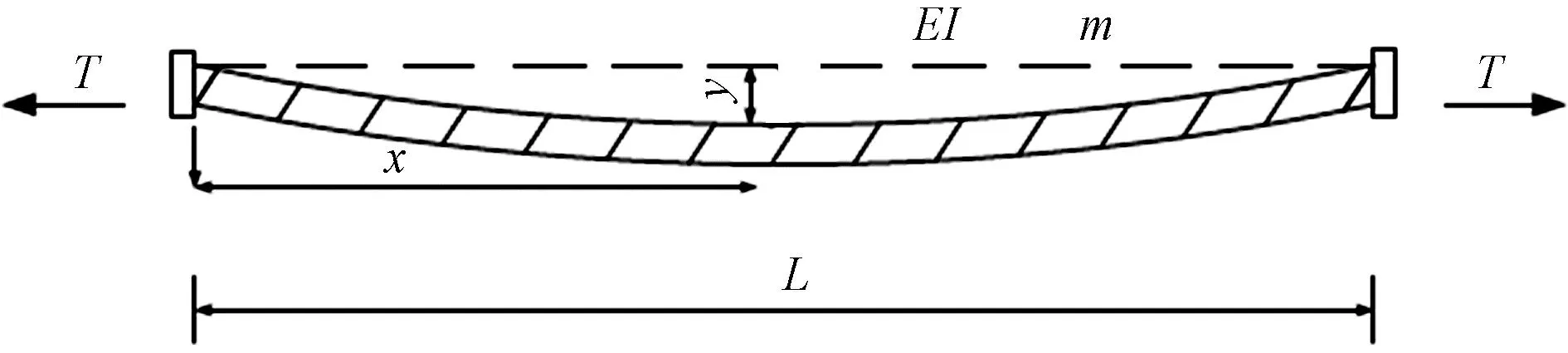
图1 拉索分析模型图

自由振动的情况下索基本微分方程为:

(1)

分离变量法求解,设:

y(x,t)=Y(x)·S(t)

(2)

对索的自由振动方程进行处理,可得:

(3)

将其分解为两个常微分方程:

(4)

(5)

式中:T为索力;EI为抗弯刚度;m为索的单位质量;L为索的长度;x为索的弦向坐标;y为平面内横向振动的振动位移;t为时间;ω为频率。

由于拉索两端边界约束情况不同,拉索振动模态也会有所改变,需要根据工程实际情况确定拉索两端的约束条件。在复杂边界条件下,频率方程难以获得显式的索力与频率对应关系。

1.2 振动频率法索力测试

振动频率法索力测试是将灵敏的加速度拾振器固定在拉索上,通过外界环境激励获得索体振动信号的检测方法。拾振器所得加速度信号进行一系列处理后,经过频谱分析可以得到拉索实测自振频率。利用自振频率与拉索索力间的函数关系确定索力。

基于此,在进一步考虑拉索两端及局部支撑构造等边界条件基础上,建立预应力拉索的计算模型,如图2所示。其中kw为拉索两端固定点转动刚度;k为减震器或转向块的支撑刚度;LO为划分单元长度;A为拉索截面面积。拉索索力计算流程图如图3所示。

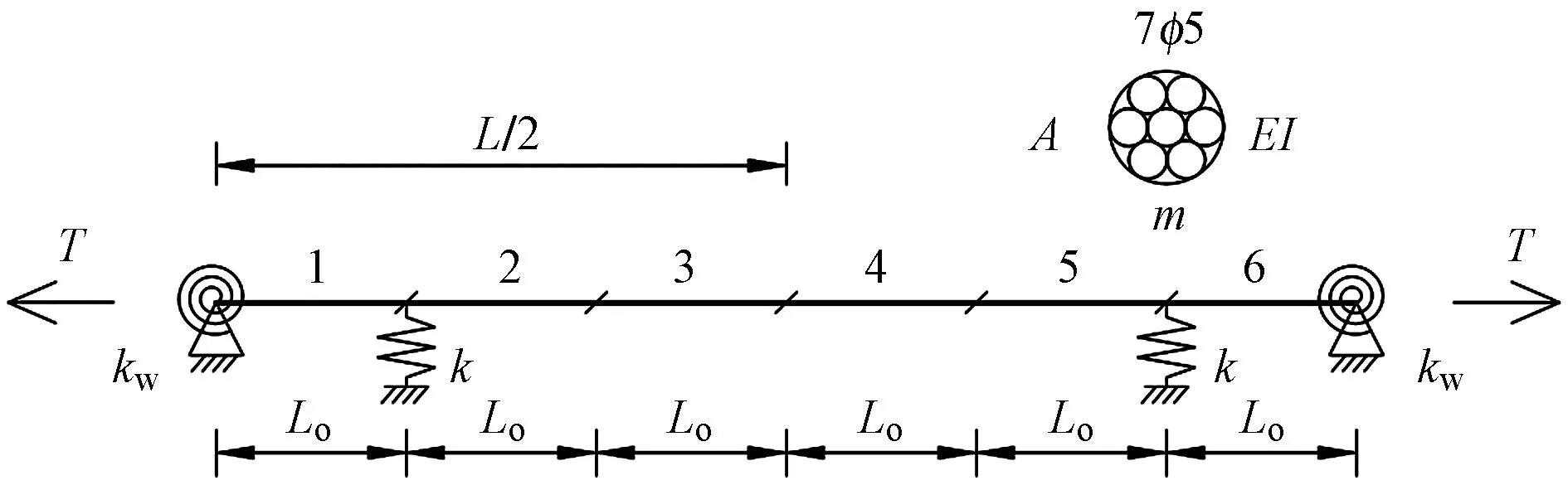
图2 索力计算示意图

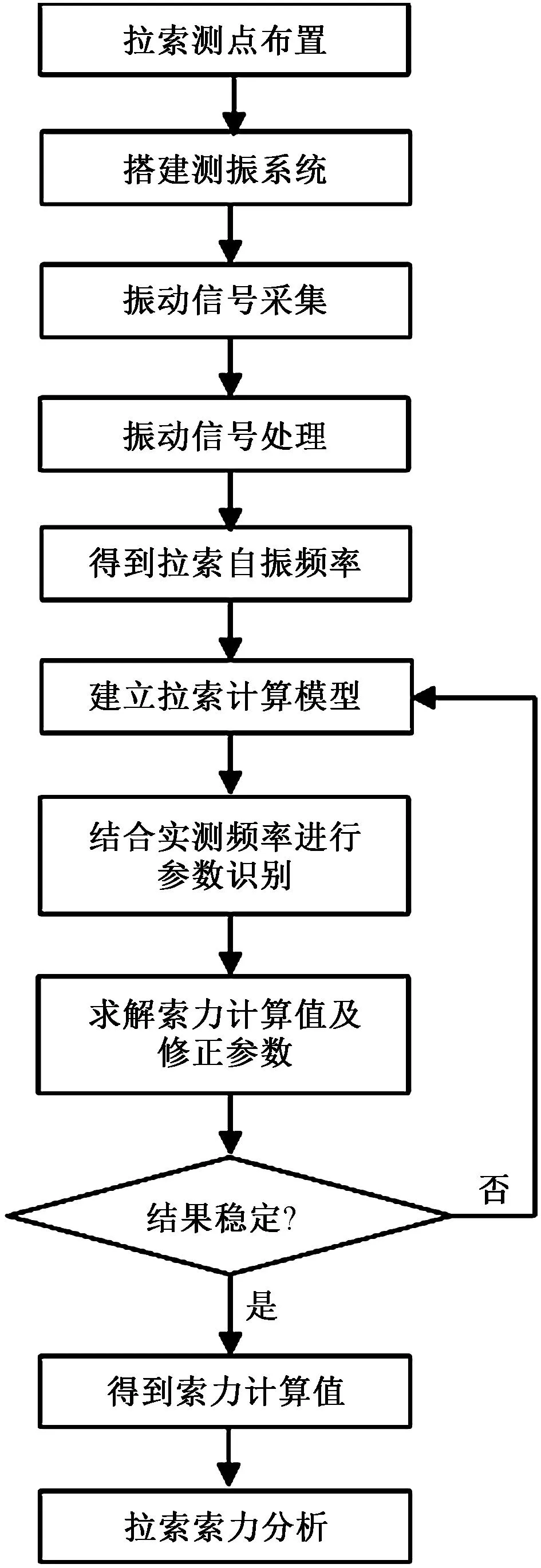
图3 索力计算流程图

采用有限元法对拉索进行振动分析,拉索振动方程表示为:

(6)

式中:M为拉索质量矩阵;K为拉索刚度矩阵,K=KL+KO,其中KL为拉索线弹性刚度矩阵,与抗弯刚度EI有关;KO为初应力刚度矩阵,与索力T有关。

若忽略结构阻尼C及外荷载F,可得自由振动频率方程:

(7)

将振动位移U表示为正弦级数,可得:

(8)

考虑振型间质量矩阵和刚度矩阵的正交性,得到如下特征方程:

(K-ω2M)Φ=0

(9)

式中:ω为拉索固有圆频率,ω=2πf,f为拉索固有频率;Φ为拉索振型。

若给定索力T,初应力刚度矩阵KO可通过对图2拉索模型进行静力求解,即利用矩阵位移法求解已知索力T作用下的初应力刚度矩阵KO。求解式(9)即可得到T作用下预应力拉索的各阶固有频率fi(i=1,2…,n)及拉索振型函数,其中i为频率阶数,n为最高阶频率阶数。

采用识别技术可以准确识别有限元中难以获取的边界条件。考虑长期运营结构存在损伤,导致实际参数与设计参数有一定差距,可以利用能量法对有限元计算所得近似的振型函数进行积分,代入实测频率值进行识别。

任意时刻拉索动能Ek为:

(10)

任意时刻拉索势能Ep为:

(11)

令最大动能等于最大势能可得:

(12)

识别参数包括索力T、抗弯刚度EI、弹簧刚度kw及支座刚度k,需结合多阶实测频率联立线性方程组进行求解。求解所得计算索力值及修正刚度参数经过与设计参数对比后,将变化较大的参数替换至有限元模型重新计算,以获得修正拉索振型。

将修正拉索振型函数及实测频率再次代入式(12)联立线性方程组,解出相应的二次计算索力值和二次修正刚度参数,直到计算结果趋于稳定,停止上述步骤,以达到测试预应力拉索索力值与实际索力值接近的目的。

2 工程概况

2.1 体育馆概况

某体育馆于1996年竣工,至今已运营26年,屋盖采用六点支承的大跨度预应力组合式双曲抛物面双层扭网壳钢结构。全馆采用6个单轴对称的双层扭网壳组合而成,中间设有三向网架式六边形中央采光井,6个扭网壳的中央角点和中央的三向网架相连。扭网壳钢结构由6根钢筋混凝土柱支撑,柱顶端设置支座球,支座球是两个扭网壳预应力拉索的锚固点。钢结构柱跨68.418m,角悬挑11.4025m,对角长度91.223m,网壳展开面积约6000 m2。体育馆内部网架结构与网壳结构三维简图如图4、5所示。

图4 体育馆内部网架结构

2.2 体育馆预应力拉索形式及布置情况

预应力拉索位于六边形扭网壳钢结构的六条边,每侧采用4根7×7φ5钢绞线,拉索整体布置情况如图5红色线条所示。两相邻交叉拉索在支座球内交叉锚固,为了保证拉索合力中心位置和防止拉索位置重合,采用两种拉索布置形式,如图6、7所示,其中一组拉索围绕中心旋转45°进行布置,如图8、9所示。

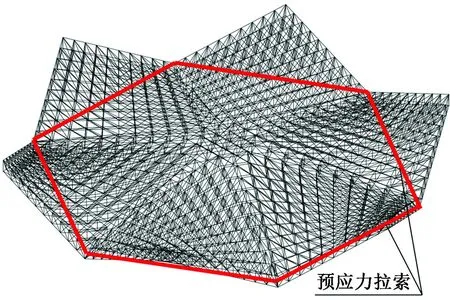
图5 网壳结构三维简图

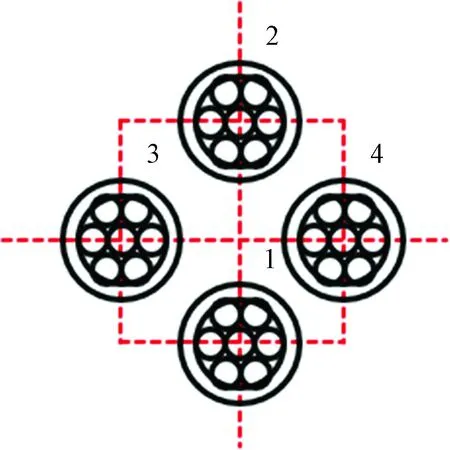
图6 拉索1型布置图

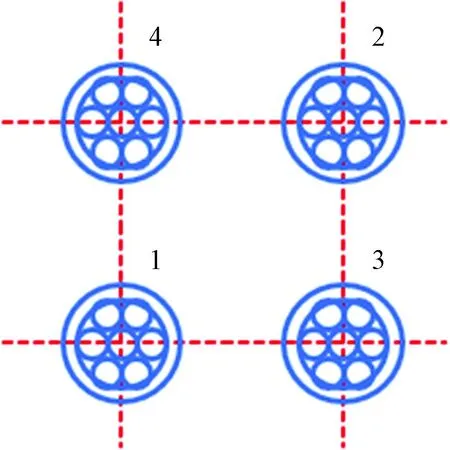
图7 拉索2型布置图

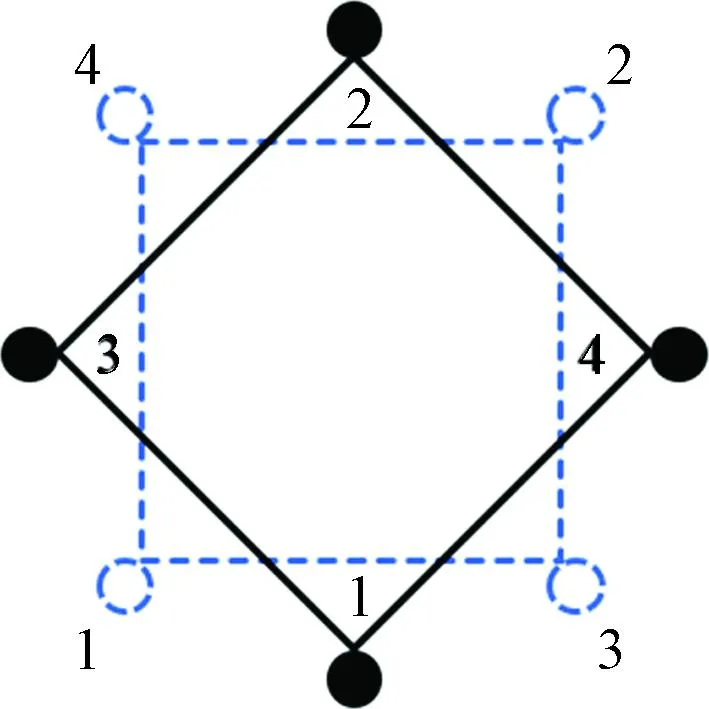
图8 支座球交叉锚固示意图

图9 支座球交叉锚固图

拉索预应力分3次等量张拉完成,最后在支座球开孔处压力灌入C30细石混凝土形成固端双保险。体育馆西门所对应的支座编号为1号,从1号支座按逆时针方向依次为4号、3号、6号、2号、5号支座,对支座间各套拉索的编号也按照逆时针方向选取,6套拉索编号分别为1-4、4-3、3-6、6-2、2-5、5-1,每套拉索中有4根拉索,再分别编号为1、2、3、4。预应力拉索1-4现场实际情况如图10所示。

3 现场测试

由于拉索较长,沿拉索全长等间距布置多个测点会大大增加布置难度和工作量,造成多方面误差干扰,综合考虑后取拉索各边中点为测点,通过标记各边拉索中点并安装传感器。图11为预应力拉索拾振测点布置点位,图12为传感器现场安装情况。

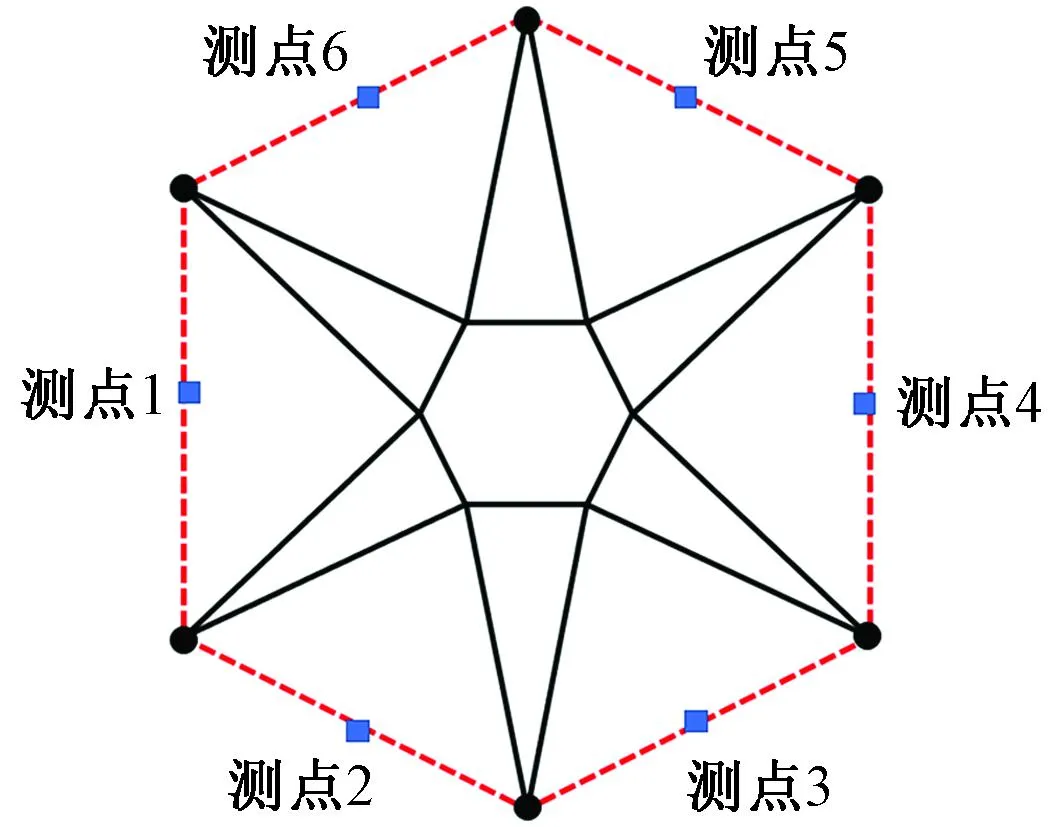
图11 测点布置平面图

图12 测点布设

借助自然脉动来获得索体的振动信号,将加速度传感器稳固布设至标记位置后,连通DHDAS动态信号采集分析系统,单次采样时长1996s,采样频率200Hz,频率分辨率为0.122Hz。表1为通过快速傅里叶变换后的预应力拉索振动前四阶频率。

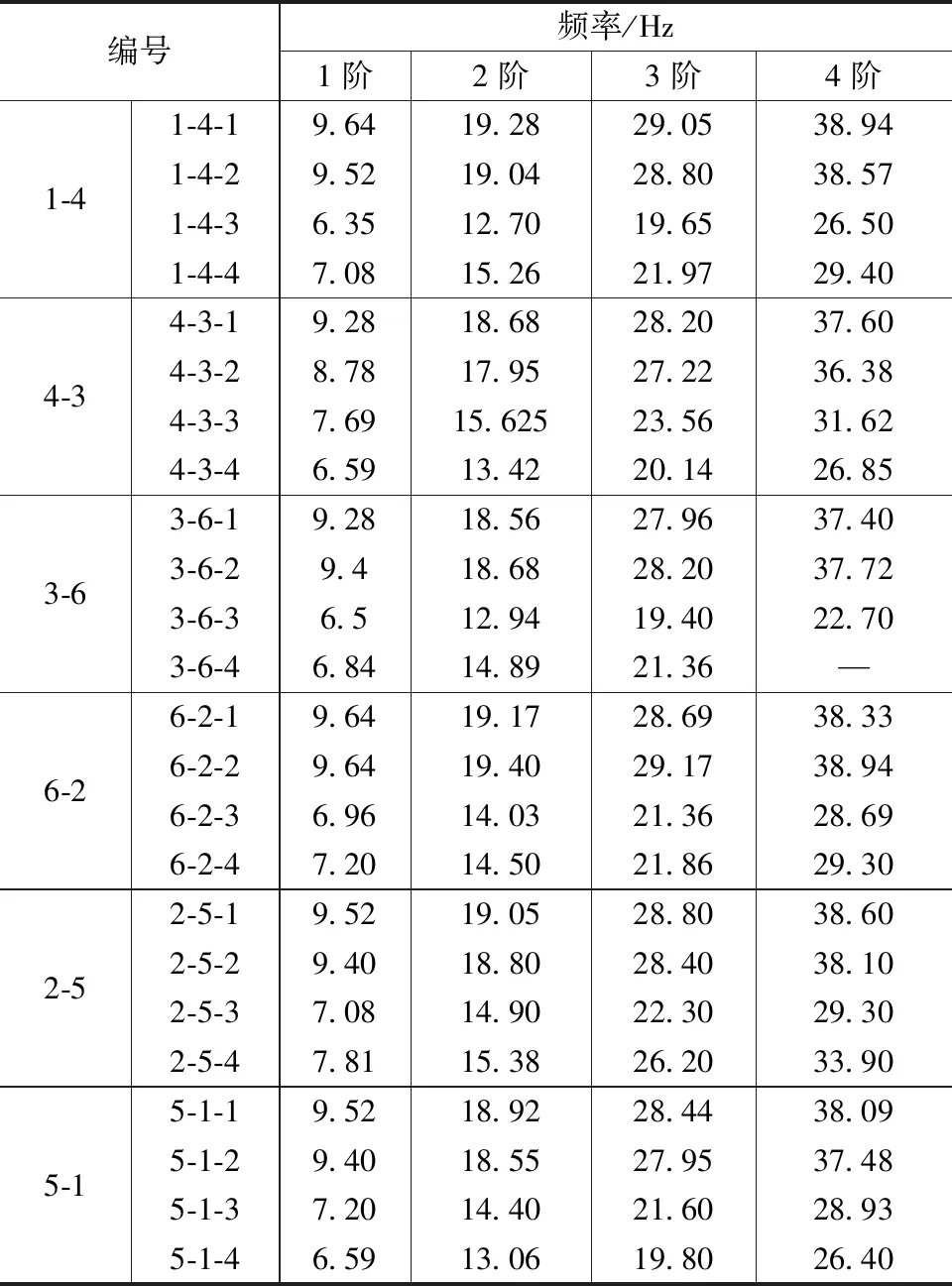
表1 拉索前四阶振动频率

4 索力计算

将前四阶固有频率代入式(12)进行反复验算,可得各拉索现阶段索力情况。图13、14分别为拉索1-4-1振动时程曲线和频谱图,将所得实测频率代入前文方法计算,可得该拉索索力。经计算,体育馆预应力拉索索力如表2所示。

图13 拉索1-4-1时程图

图14 拉索1-4-1第1阶至第4阶频谱图

预应力拉索在施工阶段和运营阶段均会产生预应力损失,主要包括锚固损失、摩擦损失、松弛损失及徐变损失等,造成拉索索力实际值与设计值存在差距。由表2可知,采用本文方法识别出的预应力拉索索力,索力计算值均小于设计值,索力损失大致为0.28%～51.65%。当拉索索力损失过大且影响到结构安全时,可通过加大构件截面、改变结构体系、增设支撑及预应力补张等可靠加固措施对结构进行加固。

5 结论

(1)大跨度空间结构拉索的索力识别,可通过现场测试加速度振动数据,进而得到多阶振动频率,并结合有限元方法即可迭代获取拉索参数,并计算出拉索索力。

(2)对某体育馆进行预应力拉索索力测试,用本文提出方法对该结构所有拉索进行有限元建模、数据采集及索力计算,并与其设计值进行对比,可以得到目前结构中拉索索力损失程度。结果表明,体育馆运营26年后,拉索索力计算值相比于设计值下降0.28%～51.65%,索力下降均值为21.2%。需进一步采取加固措施,对预应力损失较大拉索补充预应力。