采用多任务学习预测短时公交客流

张鹏祯，左兴权，黄 海

1.北京邮电大学 计算机学院，北京 100876

2.可信分布式计算与服务教育部重点实验室，北京 100876

公交客流预测根据过去一段时间的客流量及其相关信息来预测未来一段时间内的客流量，对公交系统的组织和运营具有重要意义[1]。公交短时客流预测一般指预测未来5～15 min 的客流，主要包括两种模型：线性预测模型和非线性预测模型。线性预测模型包括自回归移动平均（autoregressive integrated moving average，ARIMA）模型[2]、卡尔曼滤波（Kalman filtering）模型[3]等，这类模型具有实现简单、预测结果稳定的优点，但只适用于平稳的时间序列预测，无法捕捉客流的时变性和随机性带来的复杂非线性关系。非线性模型包括支持向量回归（support vector regression，SVR）模型[4]、最小二乘支持向量机（least squares support vector machine，LSSVM）模型[5]，以及深度置信网络[6]（deep belief network，DBN）、栈式自动编码器[7]（stacked autoencoder，SAE）和长短期记忆网络[8]（long short-term memory，LSTM）等深度学习模型。

当前公交短时客流预测方法主要利用单条线路的客流进行预测，忽略了多条线路客流之间的相似性对客流预测的提升效果。通过分析公交乘客刷卡数据，发现一些公交线路的客流量波动趋势存在相似性，组合多条线路更能刻画客流量的整体分布趋势，减少由于过度拟合导致的预测精度下降情况。此外，引入其他公交线路的客流也有利于捕捉当前线路的客流量实时波动情况。在公交实际运行过程中，客流量的变化和分布往往受到诸多因素影响，近期的客流对于预测任务具有更高的参考价值，但时间跨度的缩短会导致因数据量不足而难以拟合客流趋势的问题，多条线路同时预测扩大了训练数据的规模，可以在一定程度上弥补这一问题。鉴于此，引入多任务学习方法来建立公交客流预测模型。

多任务学习（multi-task learning，MTL）同时考虑多个相关任务的学习过程，其目的在于利用任务间的内在关系来提高单个任务学习的泛化性能[9]，进而改善任务的学习效果。对于需要大量标注数据的监督机器学习方法，多任务学习框架可以帮助目标任务利用其他任务的经验信息，有效缓解数据需求的压力并防止学习资源的浪费。目前，多任务深度学习已被用于多个领域的时间序列预测问题，已有研究表明[10-12]：多任务学习框架可以隐式地捕捉多个时间序列之间的动态关系，提高时间序列预测的精度。

近些年，一些研究将多任务学习用于城市交通客流预测问题。Zhong等[13]融合公交、地铁、出租车等多元客流数据，通过正则化方式建立多任务学习模型，预测区域内的未来客流。Bai等[14]利用多任务框架预测区域内的出租车乘客人数，根据兴趣点（point of interest，POI）信息和历史乘客需求为每个目标区域选择相似区域，并利用卷积神经网络提取它们的空间相关性。Chidlovskii[15]将城市公交网络划分为多个区域，利用多任务支持向量机算法预测每个区域的上车乘客数目。Luo等[16]将多任务学习用于单条公交线路的细粒度客流预测，利用车载客流和上下车客流来构建预测模型。当前还没有借助多任务学习，利用多条公交线路的客流信息来提升客流预测效果的研究。

多任务学习本质上是一种归纳迁移机制，该方法基于共享表示并行训练任务，在并行训练的同时分享不同任务学到的知识，将相关任务训练数据中包含的领域信息作为一种诱导偏差[17]。本文将多任务学习引入到公交客流预测中，提出一种基于多任务学习的公交短期客流预测方法（multi-task learning based method for short term bus passenger flow prediction，MTL-BFP），利用多条相关线路的客流预测任务来约束深度学习模型的潜在共享参数。首先，利用灰色关联分析法[18]（grey relation analysis，GRA）和皮尔逊相关系数[19]（Pearson correlation coefficient，PCC）获取不同公交线路客流量之间的相关关系；然后，将与当前线路相关度高的若干线路的客流预测任务作为辅助任务，建立了一个硬参数共享的多任务循环神经网络预测模型，模型利用门控循环单元（gate recurrent unit，GRU）神经网络来捕捉客流的时序特征。将该模型用于真实公交线路的短时客流预测，实验结果表明，该模型在预测精度方面优于传统时间序列预测模型以及仅考虑单条线路客流的神经网络预测模型。

1 多任务客流预测问题

本文利用当前公交线路及其相关线路的历史客流量数据和时间特征信息，预测当前线路未来一个时间步长的上车客流量，即在该时间步长内的上车总人数。

本文将公交路网描述为一个有权无向图G=(V,E,W)。集合V中每个节点代表一条公交线路，|V|=N为公交线路的数量；边集合E表示线路之间的相关关系；W=RN×N为相关度系数矩阵，其中元素分别表示线路Li和Lj间的皮尔逊相关系数和灰色关联度系数，i=1,2,…,N,j=1,2,…,N。对于目标预测线路（即要预测客流的线路）Lk,用前s步的特征信息X={xt-s,xt-s+1,…,xt-1}来预测下一步的客流Yt。

公交线网由多条公交线路组成，公交线路的客流一般具有高峰、平峰、低峰时间段，不同公交线路的客流分布呈现一定的相似性。特别是经过共同区域或者存在换乘关系的一些公交线路，它们的客流存在时空相关性。

多任务学习框架可以同时训练多个客流分布具有相关性或相近性的客流预测任务，并在底层共享参数，帮助模型聚焦到多个任务共同反应的特征，提高预测精度，因此本文利用多任务学习模型来预测当前线路的客流。

2 多任务学习预测方法

多任务深度学习主要分为两种，硬参数共享和软参数共享。基于硬参数共享的多任务学习方法在神经网络的底层共享参数，学习公共特征子空间；在高层为特定任务建立特定网络模型，各个模型之间相互独立，用于保留更多的任务个性特征。在共享层中，所有任务的参数是完全相同的，以此有效防止过拟合问题，提高模型泛化能力。在软参数共享模式中，每个任务都有各自的参数和模型，参数之间通过正则化距离约束在一起，任务之间的参数相似但不同。

对于公交线路的短时客流预测任务，本文利用多任务学习方式约束深度学习模型中的底层参数，通过共享层中的共享表示引导模型学习多条线路的客流量波动趋势，提高模型参数的通用性，降低模型对数据波动的敏感性，进而改善模型的预测效果。

MTL-BFP的流程如图1所示。首先利用2.2节中的方法计算所有线路之间的相关系数；然后，利用2.3节中的方法筛选目标预测线路的相关线路；接着，按2.1节中的方法构造目标预测线路及相关线路的特征矩阵，作为多任务深度学习模型的输入。多任务学习模型经过训练后，用于客流预测。

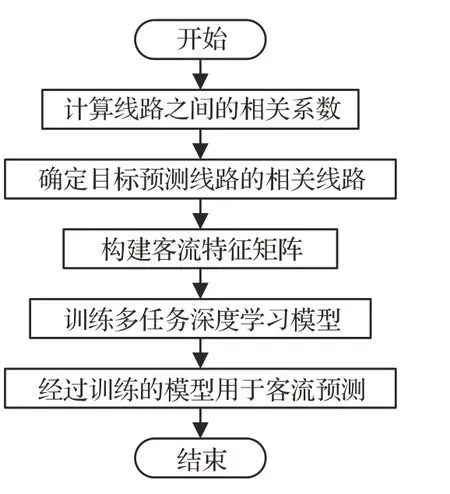
图1 MTL-BFP的流程图Fig.1 Flow chart of MTL-BFP

2.1 多任务深度学习模型

本文使用硬参数共享模式建立多任务深度学习模型，如图2所示。模型中的每个任务都代表一条公交线路的短时客流预测任务，所涉及线路包括目标预测线路及其相关线路。假设有n+1 个任务，则第0个任务为目标线路的预测任务，第1到n个任务为相关线路的预测任务。每个任务都有一个私有模块（全连接层），用于拟合单条公交线路的客流特征。此外，模型还包括一个共享模块用于共享网络参数，该模块由两个GRU 模块和一个全连接模块组成，用于学习公交线路客流分布的时序特征。模型输出为各任务对应的n+1 个线路的客流预测值。

图2 多任务深度学习模型Fig.2 Multi-task deep learning model

模型的输入为n+1 条线路前s步的特征信息，包括每步的时间信息、目标预测线路的客流量l0以及相关线路的客流量li,i=1,2,…,n，见图3。时间信息包括工作日信息（周一到周五）和时间片序号（以ts分钟为一个时间片，每天的时间片从0开始编号）。构建输入特征时，将时间信息转换为独热编码，所有线路的客流量归一化到[0，1]区间。

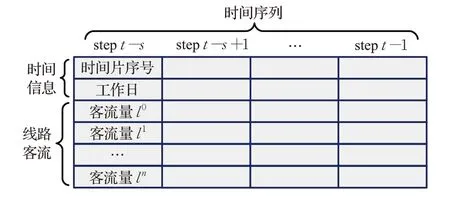
图3 模型的输入特征Fig.3 Input features of model

2.2 线路相关性度量

本文通过PCC和GRA对不同公交线路客流在时间上的分布进行相关性度量，进而获取目标预测线路的相关线路。

PCC常用来度量两个随机变量之间的线性相关性，取值范围为[-1,1]。相关系数大于零表示正相关，小于零表示负相关；绝对值越接近于1，相关性越强，越接近于0，相关性越弱。一般认为大于0.6时为强相关。具体的计算公式如下：

本文进一步用GRA来分析客流分布的相关性。GRA适用于解决多因素、多变量之间复杂关系的问题[20]，可用于探究变量之间的非线性相关性，其根据参考序列和若干个比较序列的曲线几何形状相似程度来判断关联性。GRA的取值范围为[0，1]，值越大表示关联性越强。具体计算步骤如下：

（1）设定参考序列δ0。将目标预测线路的客流量时间序列设定为母序列，记为：

（2）设定比较序列δ′：

其中，m表示参与计算的公交线路总数。

（3）利用均值法对参考序列和比较序列进行归一化处理：

其中，k=0,1,…,m；i=1,2,…,P。

（4）计算每个比较序列与参考序列对应元素的关联度系数。

其中，k=1,2,…,m；i=1,2,…,P；ρ为分辨系数，0<ρ<1,ρ越小，关联系数间差异越大，区分能力越强。本文ρ取值0.5。

（5）计算关联度。分别计算参考序列与比较序列各个对应时间步长上的关联系数，并求其均值，作为参考序列与比较序列关联度的量化表示：

其中，k=1,2,…,m。

2.3 选取相关线路

多任务学习利用正则化和迁移学习改进所有任务的预测效果，然而在实践中，多任务学习模型并不总是在所有任务上都优于相应的单任务模型。尤其是当模型参数在所有任务之间广泛共享时，任务差异带来的固有冲突可能会损害部分任务的预测精度[21]。当任务之间相差甚远时，底层共享网络将失去意义。

为保证输入到模型中的各任务具有较高相关性，本文设计了一个结合GRA 和PCC 的方法（GRA-PCC）用于选取相关线路。该方法考虑相关线路与目标预测线路间相关性的同时，也考虑了相关线路之间的相关性，具体步骤如下：

（1）设V为所有公交线路的集合；N为公交线路的总数。

（2）计算线路之间的相关度系数矩阵W，其中Wi,j=，包含线路i和线路j之间的皮尔逊相关系数和灰色关联度系数。

（3）对于目标预测线路Lk，设Vk为Lk及其已被选择的相关线路的集合；Nk为Vk中线路数量；令Vk={Lk}。

（4）计算剩余候选线路集合V′=V-Vk。

（5）计算V′中每条线路的相关度系数，构成集合，其中表示集合V′中的第j条线路与集合Vk中所有线路的平均灰色关联度系数。

（6）根据w′，从V′选取平均灰色关联度系数最大且与Vk中的任一线路的皮尔逊相关系数均大于0.6 的线路；若存在这样的线路，则将其添加到Vk中，否则算法结束。

（7）若V′≠∅或Nk≠n，返回步骤（4）；否则，算法结束。

算法计算每条候选线路与所有已经被选择的相关线路的灰色关联系数，用其平均值代表候选线路与Vk中所有线路的总体关联程度，通过皮尔逊相关系数进一步确定每两条线路之间的相关程度，进而保证模型输入任务的相关性。最终得到的集合Vk中的线路作为目标预测线路Lk的相关线路（包含目标线路Lk），输入到GRU模型。

2.4 GRU模型

GRU 是由Cho等[22]于2014年提出的一种循环神经网络，一定程度上解决了传统RNN 中存在的梯度消失问题和长期依赖问题，其与LSTM 类似，但进一步简化了神经元的结构，将LSTM中的遗忘门和输入门合并成为一个更新门，因而参数更少，更容易计算和收敛，却能达到和LSTM相近的效果。与LSTM相比，GRU网络的训练用时往往更少，效果也更稳定[23]，更适用于短时公交客流预测问题对实时性和稳定性的需求。

GRU 在序列学习任务中表现良好，克服了传统循环神经网络在学习长期依赖项时梯度消失和梯度爆炸的问题，已经被用于股票序列预测[24]、金融序列预测[25]、电池健康状态预测[26]等多个领域的预测问题。本文使用双层GRU 神经网络来捕捉公交线路客流量的时序特征。

GRU神经元的门控机制如图4所示。典型的GRU神经元只有更新门z和重置门r两个门控单元，这两个门控单元都用来处理xt和ht-1，其中xt表示当前时间步上公交线路客流数据的特征信息，ht-1为隐藏层h在时间步(t-1)的输出（隐藏状态），充当神经网络的记忆体，用来传递先前的客流状态信息；更新门决定了上一个时间步长的状态信息被接受的程度，其值越大说明前一个时间步长的状态信息越重要；重置门用于控制先前的隐藏状态与新的输入信息的结合情况，它的输出为传递到下一个时间步长的隐藏状态，其值越小说明先前的隐藏状态被忽略的越多。GRU网络中隐藏层的存储单元在每个时间步上的更新过程如下：

图4 GRU神经元结构Fig.4 GRU structure

其中，rt、zt、ht分别表示重置门r、更新门z、隐藏层h在第t个时间步长的输出；表示隐藏层h在第t个时间步长上的记忆体；Wr、Wz、分别表示重置门r、更新门z、隐藏层h在第t个时间步长的权重。

2.5 损失函数

多任务学习模型并行训练多条线路的客流预测任务，使用参数优化器（如Adam、SGD）自动学习优化过程中特征的交互作用，损失函数如下：

其中，Xk是预测线路Lk的客流时输入的特征矩阵，如图3所示。Yi是第i个任务对应的真实客流，θi是第i个任务的学习参数，第0个任务为线路Lk的预测任务，n是相关线路数目。本文模型的优化目标是最小化所有任务的损失和，其中损失函数为客流量预测值与真实值之间的平均绝对误差（mean absolute error，MAE）。

3 实验结果

3.1 实验数据

实验数据来自于北京市25条公交线路一个月的真实乘客上车刷卡数据，经过数据异常值及重复数据清洗后，总数据量约682万条，单条线路的数据量在5万至73万之间。按照时间维度对数据集进行划分，前80%数据为训练集，后20%数据为测试集。

将线路1、9、653、57、983 作为目标预测线路。图5（a）为这5 条线路一天内的客流分布情况（以15 min 为统计单位），其客流量均在8：00 左右和18：00 左右出现高峰，在10：00—15：59 左右趋于平稳。图5（b）为这些线路的全天总客流量在不同日期的分布情况。为了减少数据波动对模型预测效果的影响，根据客流数据分布特点，本文将数据集划分为早高峰前后（6：00—9：59）、平稳时段（10：00—15：59）和晚高峰前后（16：00—21：59）三个时间段，分别构建输入序列样本。

图5 线路的客流分布情况Fig.5 Passenger flow distribution of bus lines

3.2 比较算法与评估指标

将提出的MTL-BFP方法与下列算法对比。这些比较算法采用单步预测方式：

（1）历史平均（history average，HA）：利用过去一段时间内的客流量平均值作为未来客流量的预测结果。

（2）ARIMA[2]：一种统计学习方法，考虑差分、自回归和移动平均分量来分离信号和噪声，广泛应用于各种时间序列任务。

（3）SVR[4]：支持向量机的一个重要分支，通过优化样本点到超平面的距离得到最小训练模型，用来回归问题。

（4）循环神经网络[27]（recurrent neural network，RNN）：一类用于处理序列数据的神经网络，在序列的演进方向进行递归且所有节点按链式连接，基于多时间步历史数据进行预测。

（5）GRU模型[22]：一种循环神经网络，适用于序列学习，可以在一定程度上解决梯度爆炸问题。

（6）MTL-RNN 模型：多任务版本的循环神经网络模型MTL-RNN，与MTL-BFP模型的差别在于使用RNN替换模型中的GRU网络，用来评估GRU网络在多任务框架下对客流特征的捕捉性能。

使用平均绝对误差MAE、平均绝对百分比误差（mean absolute percent error，MAPE）和均方根误差（root mean square error，RMSE）来评估客流预测结果。误差值越小，模型预测效果越好。

其中，q为预测客流的时间片个数，yi为真实的客流值，为预测的客流值。

3.3 实验参数设置

实验中，所有模型的时间步长ts均为15 min，神经网络模型输入序列长度s设为15。GRU模型和MTL-BFP模型中的两层GRU 结点数从下到上分别设为128 和64，激活函数为ReLU；底层Dense 的结点数设为64，各个任务独立的Dense结点数为16，激活函数均为Linear。对比模型RNN、MTL-RNN中的RNN结点数和MTL-BFP模型中的GRU结点数相同，Dense层结构保持一致。利用tensorflow2 的keras 模块搭建神经网络模型，使用初始学习率为0.001的Adam优化器优化模型。实验的批次大小取64，迭代次数设为80。模型HA、ARIMA、SVR的参数设置如表1所示。

表1 HA、ARIMA、SVR的参数设置Table 1 Parameter setting of HA，ARIMA and SVR

当参与训练的相关线路数目n值较小时，线路之间的相关性高，但模型泛化能力较差，不同时段客流预测结果差异明显；当n值较大时，则难以保证足够的相关线路数目以及线路之间的相关性。通过少量实验，将n设为4。

3.4 实验结果及分析

用GRA-PCC 方法筛选目标预测线路的相关线路，被选中的相关线路与其对应目标线路的相关性度量值如表2 所示。其中，灰色关联度系数均在0.79 以上，皮尔逊相关系数均在0.67以上，表明目标线路与相关线路为强相关，其客流分布呈现一定的相似性，符合多任务学习模型对任务相关性的要求。

表2 目标预测线路的相关线路及其相似性度量值Table 2 Related lines of target prediction lines and their similarity measures

为了证明GRA-PCC 方法的有效性，随机选取4 条线路与GRA-PCC方法选取的4条线路进行客流量预测实验对比，结果如表3 所示。与随机选取方法相比，采用GRA-PCC方法的预测效果在MAPE上降低了3.1%～5.9%，在MAE和RMSE上也表现更好。

表3 GRA-PCC和随机选择线路方法的预测结果对比Table 3 Comparison of prediction results of GRA-PCC and approach of selecting lines randomly

表4比较了各算法应用于5条线路的预测结果。从表4可看出，深度学习模型（RNN、MTL-RNN、GRU、MTLBFP）的预测效果明显优于其他算法（HA、ARIMA、SVR）。对于神经网络模型，相比RNN、MTL-RNN 的MAPE 降低了5.2%～9.1%；相比GRU、MTL-BFP的MAPE降低了3.2%～8.4%，这说明多任务学习可有效地降低预测误差。相比于MTL-RNN，MTL-BFP模型在线路9、653、57、983 上的预测效果在各个指标上表现更好，MAPE 降低了1.5%～6.2%。对于线路1，MTL-BFP 相比MTL-RNN在MAPE 指标上表现略差，但在其MAE 和RMSE 指标更优，这说明GRU网络可以更好地捕捉客流的变化特征。

表4 MTL-BFP与其他方法的预测结果对比Table 4 Comparison of prediction results of MTL-BFP and other approaches

4 结论

针对公交线路的短时客流预测问题，本文利用多任务学习框架引入相关线路的短时客流预测任务，建立了一个多任务循环神经网络模型。该模型利用GRU网络捕捉客流的时序特征，在底层网络中共享参数以提高泛化能力，并利用每个任务的私有模块保留个性特征。本文设计了一个基于灰色关联法和皮尔逊相关系数的相关线路筛选方法，用以保证多条线路客流预测任务之间的相关性，进而提升多任务模型预测效果。

将本文方法用于真实公交线路的客流预测，实验证明：本文设计的相关线路筛选方法是有效性的，建立的多任务模型可有效提升公交线路短时客流预测的准确性。

未来的研究方向包括：进一步研究多任务学习模型的构建方法，并引入更多客流特征和时空特征，从而进一步提高客流预测的准确性。