基于路径评价模型的自适应轨迹跟踪控制

许 万，周 航

湖北工业大学 机械工程学院，武汉 430068

移动机器人因其具有机动性能灵活、承载性能优越等特点被应用在室内建筑施工中的自动化放线领域[1]。其中，轨迹跟踪控制是移动机器人自主导航过程的关键一环，控制器的性能将直接影响行驶精度[2]。

当前，主流控制方法包括：PID 控制、Backstepping控制、模糊控制、滑模控制、自抗扰控制、MPC 控制、神经网络控制等[3]。然而，上述控制器在控制增益的选取、模糊规则表的确定、论域的设立等方面普遍需要通过人为试凑的方式，存在控制器调试困难等缺点，同时控制器鲁棒性较差，容易受到外界扰动的干扰，并且当外界环境发生变化时，控制增益需要进行重新设定[4]。考虑到复杂环境下的控制需求较为严格，采用固定的控制增益难以确保跟踪精度，文献[5]提出了一种自适应模糊PID 控制方法，实现了对控制增益的自整定，同时也提高了移动机器人的抗扰能力；文献[6]利用神经网络非线性建模能力强的特点，将该方法与Backstepping 控制器进行结合，其中Backstepping 方法能将高阶系统进行降阶处理，简化控制模型，提升控制性能，具有较高的响应速度，同时利用神经网络实现控制增益的自适应调整；文献[7]提出了一种改进自适应模型预测控制，能有效地建模和控制非线性系统，在曲线行驶、圆弧转弯时提供更精确的控制策略；文献[8]设计了一种自适应滑模控制器，减少了传统滑模控制的高频振荡现象，提高了控制器的平滑性和稳定性。考虑到机器人模型不确定会对跟踪精度产生影响，文献[9]将移动机器人实际运行中不可避免的车轮磨损、主轴形变、加工误差、装配误差等因素考虑在内，自适应调整运动学模型，基于动态运动学模型设计出的控制器跟踪精度更高。考虑到动力学对控制器的影响，文献[10]针对移动机器人在行驶的过程中支撑轮的扭转会对机器人产生扰动，影响轨迹跟踪性能，进而将该扰动作为前馈输入设计自适应控制器；文献[11]针对机器人行驶在颠簸路面、湿滑路面以及松软路面时车轮会发生纵向或侧向滑动，设计了一种能够在未知滑动参数情况下自动调整增益的控制器。

综上所述，采用自适应机制能够有效地增强轨迹跟踪的性能。但是，上述研究成果均未考虑路径曲率对轨迹跟踪控制的影响。

文献[12-13]指出，移动机器人的轨迹跟踪控制会受到路径信息的影响，尤其是路径的曲率及曲率变化率这两个物理量会直接影响机器人的控制精度。在理论跟踪轨迹弯道较多、曲率变化较大的路况下，移动机器人轨迹跟踪控制难度显著提升。文献[14-15]通过研究人类驾驶员的行车经验，总结出驾驶技术高超的人类驾驶员会通过综合分析前方道路弯曲程度与车身目前状态之间的关系，提前做出控制决策，从而提升驾驶安全性。基于上述研究成果，为了进一步提高智能移动放线机器人轨迹跟踪控制精度，借鉴人类驾驶员在控制车辆时会综合考虑前方道路弯曲程度与汽车位姿的驾驶经验，设计了一种基于路径评价模型的自适应轨迹跟踪控制器。首先，建立移动机器人的运动学模型以及位姿误差模型；其次，建立了路径评价模型，定义了路径复杂度的概念，并设计一种路径评价函数，该函数能对当前路径曲率及车辆跟踪误差进行量化分析；然后，为了验证路径评价模型的可行性，设计了一种自适应Backstepping控制器，将路径评价函数的结果作为BP神经网络的输入，控制增益作为BP神经网络的输出，进而实现Backstepping控制器的自适应控制；最后，通过仿真和实验证明了路径评价模型能有效提高轨迹跟踪精度，同时还通过实验法给出了路径评价模型中核心参数的合理取值范围。

1 移动机器人模型

1.1 运动学模型

以智能移动放线机器人为研究对象，其轮系结构为麦克纳姆轮，假设移动机器人在行驶过程中车轮与地面间不发生打滑现象，麦克纳姆轮各辊子主轴线与车轮主轴线呈45°夹角，构建如图1所示的运动学模型。

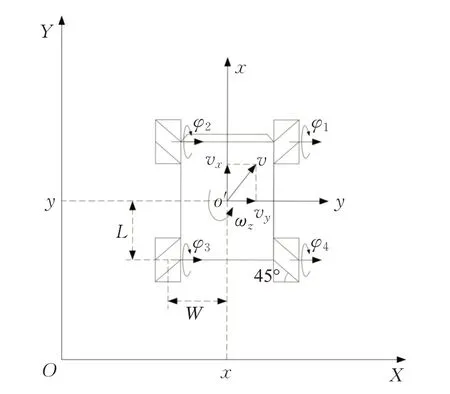
图1 运动学模型Fig.1 Kinematic model

图1中，XOY为全局坐标系，xo′y为局部坐标系，o′为移动机器人底盘的几何中心，坐标(x,y)为机器人的全局位置，vx、vy为机器人线速度v在局部坐标系xo′y中的速度分量，ωz为机器人角速度，φ为车轮转速，W和L分别为车轮轴线中点到底盘几何中心的水平和垂直间距，R为车轮的最大半径，其运动学方程可表示为[16]：

1.2 位姿误差模型

位姿误差模型如图2所示，在全局坐标系XOY中，定义Q=[x y θ]T为机器人的真实位姿向量；Qr=[xr yr θr]T为机器人的参考位姿向量；D=[Xe Ye θe]T为全局位姿误差变量；d=[xe ye θe]T为局部位姿误差变量。

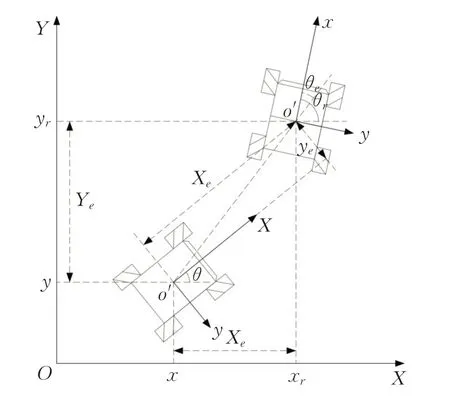
图2 位姿误差模型Fig.2 Pose error model

图2中，x、y、θ分别为机器人的全局实际坐标值及车身横摆角度，xr、yr、θr分别为机器人的全局参考坐标值及车身横摆角度，移动机器人底盘的几何中心与参考轨迹上目标点之间的位姿误差为：

对式（2）微分得：

其中，实际点上的速度与角速度分别描述为v和ω；参考点上的速度与角速度分别描述为vr和ωr。

2 路径评价函数

在传统控制器的设计过程中，通常将当前时刻下的位姿误差信息作为控制器的输入，从而控制机器人抵达目标点。但是该方法未考虑路径曲率对跟踪控制的影响，当路径的复杂度较高时，控制难度将显著增大。

为了描述移动机器人实际位姿与理论跟踪轨迹之间的关系，建立如图3 所示的路径评价模型，其中实线为“理论跟踪轨迹”，虚线为“实时规划路径”。该模型在描述移动机器人跟踪位姿误差的同时，直观反映了移动机器人与理论跟踪轨迹之间的几何关系。

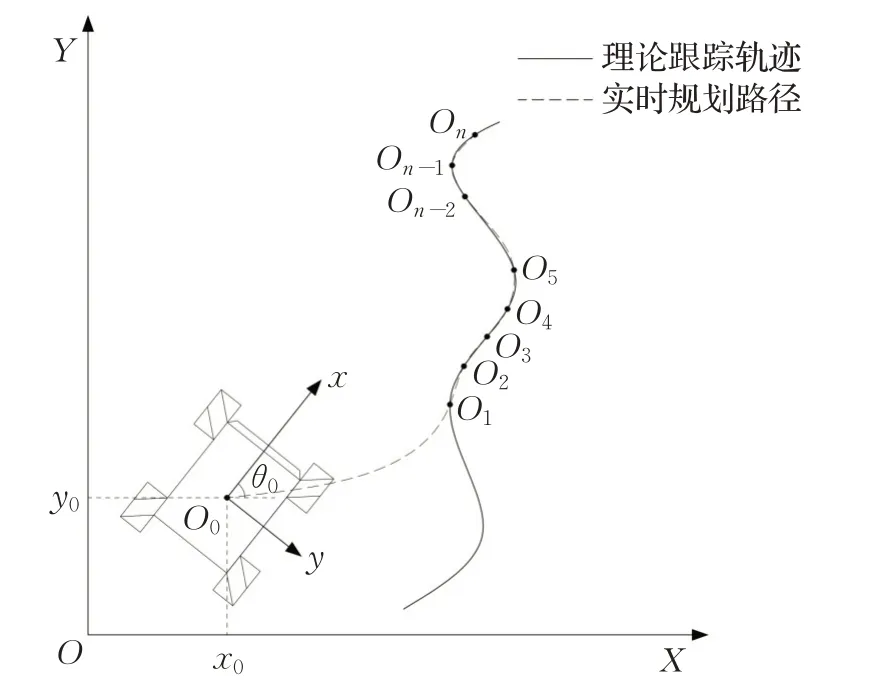
图3 路径评价模型Fig.3 Trajectory evaluation model

图3中，点O0(x0,y0,θ0)为底盘的几何中心，并且为当前时刻T下的实际位姿点；Oi(xi,yi,θi)(i∈(1,n))为理论跟踪轨迹上的离散参考点，且O1(x1,y1,θ1)为当前时刻T下的理论位姿点。

图3 所示的理论跟踪轨迹是一条与时间相关的曲线，在实际应用中通常将理论轨迹进行离散化处理，从而演变为对参考离散点进行跟踪的问题。假设离散化间隔时间为Δt,则Oi(xi,yi,θi)(i∈(1,n))为T+(i-1)Δt(i∈(1,n))时刻下的理论位姿点。

将由点O0(x0,y0,θ0)及点Oi(xi,yi,θi)(i∈(1,n))连接而成的曲线定义为实时规划路径E，同时定义与实时规划路径重合的离散参考点为“路况特征点”，其数量为n。实时规划路径E包含有当前时刻T下，O0(x0,y0,θ0)与O1(x1,y1,θ1)之间的位姿误差信息，以及未来时刻理论跟踪轨迹的曲率和曲率变化率信息。

2.1 路径评价函数的设计

根据文献[12-13]描述，移动机器人当前的位姿误差以及理论跟踪轨迹的曲率及曲率变化率信息会直接影响控制的效果。如图3所示，当前时刻T下O0与O1之间的位姿误差D能够直接描述位姿偏差情况，理论跟踪轨迹的曲率及曲率变化率信息能够量化反映道路的弯曲程度及变化程度。

因此，从路径曲率和车辆跟踪误差的角度入手，基于曲率因素及位姿误差因素设计了一种路径评价函数，能对实时规划路径E进行定量分析，具体描述如下：

式（4）描述了路况特征点Oi处的路径评价情况。其中，η(η∈(0,1))为评价函数的权值系数，权值系数的选取将直接影响评价函数的输出值，为此实验部分将定性分析权值系数的选取依据。针对实时规划路径E的路径评价函数运行流程如图4所示。

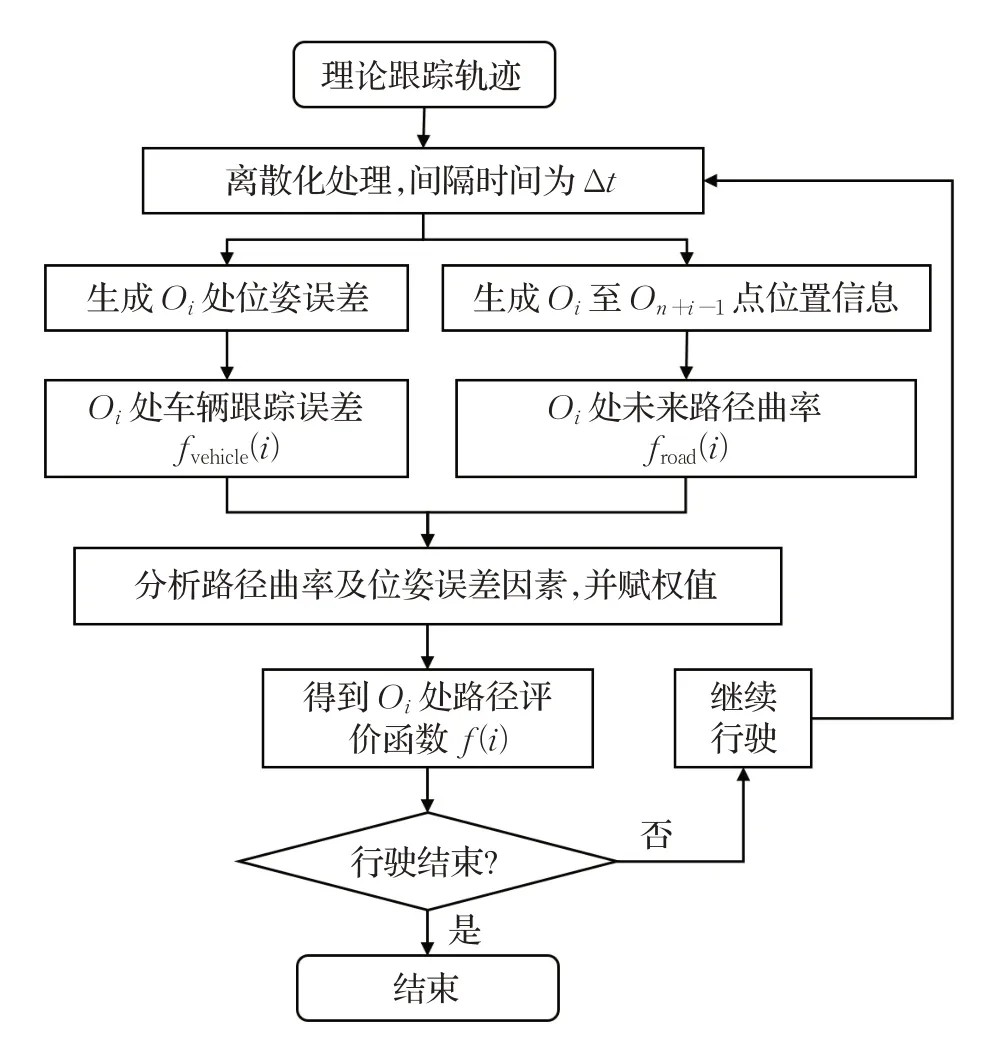
图4 路径评价函数运行流程Fig.4 Flowchart of trajectory evaluation function operation

图4中，评价函数f(i)可以系统且直观地反映了路径曲率froad(i)和车辆跟踪误差fvehicle(i)信息，为后文自适应控制器的设计提供了控制输入。其中，froad(i)及fvehicle(i)分别代表曲率因素以及位姿误差因素，具体描述如下。

2.2 路径曲率因素

图3中，剔除O0点，路况特征点O1至On处的曲率及其变化率可以描述未来(n-1)Δt时间内理论跟踪轨迹的复杂度。为了量化分析未来(n-1)Δt时间内的路径弯曲程度，引入曲率Ρ以及曲率变化率Ρ′。假设理论跟踪轨迹上一共有m个离散点，路况特征点i处归一化处理后的曲率值和曲率变化率的值ρ(i)和ρ′(i)分别表示如下：

归一化处理后的数值能够保证曲率及其变化率数量级的一致，在点Oi处，未来(n-1)Δt时间内Oi至Oi+n-1段的路径复杂度可以定义如下：

路况特征点Oi处的未来路径曲率评价函数如下：

2.3 位姿误差因素

图3中，O0O1段描述了移动机器人的位姿误差，为了量化分析当前时刻T下点O1处的误差大小，引入跟踪误差dline和横摆误差dangle，表示如下：

路况特征点Oi处的当前车辆跟踪误差评价函数如下：

3 基于路径评价模型的控制器设计

为了验证上文中路径评价模型的可行性以及路径评价函数的准确性，并进一步讨论引入上述机制能否提高移动机器人的跟踪精度，为此设计了一种基于路径评价模型的控制器，该控制器由两部分组成：Backstepping运动学控制器、BP 神经网络增益自整定控制器。控制器系统结构如图5所示。

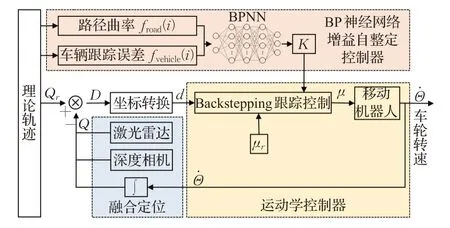
图5 TEMC系统结构Fig.5 TEMC system structure

其中，运动学控制器是以移动机器人当前时刻T下，实际位姿Q与参考位姿Qr之间的误差d以及期望速度μr作为输入，以速度μ作为输出，经过运动学逆解，控制四轮转速=[φ1φ2φ3φ4]T,从而使控制增益自整定控制器是基于BP 神经网络，以路径评价函数的值froad(i)和fvehicle(i)作为输入，以运动学控制器的增益K作为输出，从而实现自适应Backstepping控制。

3.1 Backstepping运动学控制器

基于1.1 节所建立的运动学模型及位姿误差模型，设计轨迹跟踪控制器如下：

当xe→0 时，将xe作为虚拟控制输入，取部分Lyapunov函数为：

对式（13）求导可得：

取虚拟控制输入xe的虚拟反馈为：

其中，k1为大于0的常数，f(ω)=sin(arctanω)。

将式（15）代入式（14）可得：

其中，ωsin(arctanω)在其定义域内恒为非负常数，从而可得≤0。V1正定，负定，由Lyapunov相关理论可知，在t→+∞时，ye是渐进稳定的。

对式（17）求导可得：

综上，设计控制器的核心是在输入量[v,ω]的作用下，在t→+∞时：xe=k1sin(arctanω)ye。据此，构造全局Lyapunov函数为：

对式（19）求导可得：

将式（18）代入式（20）得：

根据式（21）所设计的控制率为：

其中，k1、k2、k3为任意的正常数，分别对xe、ye、θe进行调节。

3.2 BP神经网络增益自整定控制器

式（4）所描述的路径评价函数f(i)可以量化路径曲率和车辆跟踪误差信息，也即“路径复杂度”和“位姿误差”信息。由式（22）可知，控制器中的三个增益参数k1、k2、k3会直接影响控制效果。当系统的跟踪误差发生变化，以及跟踪不同复杂度的理论轨迹时，原始控制增益K是无法保证较好的跟踪精度。

为此，综合考虑理论轨迹复杂度和位姿误差这两个输入信息，基于BP神经网络实现对控制增益K的自整定，从而提高控制器跟踪复杂路径时的跟踪精度与稳定性。所设计的BP神经网络模型输入参数为froad(i)和fvehicle(i)，输出为控制增益K。

神经网络的输出层和各隐藏层激活函数都为Relu函数：

取性能指标函数为：

利用梯度下降法修正BP 神经网络的权系数，基于BP神经网络控制增益自整定控制器运行流程如下：

（1）建立网络模型，其中隐藏层为3层，每层神经元为20个，并对各层权系数赋初始值。

（2）计算当前时刻“froad(i)”和“fvehicle(i)”。

（3）将路径评价函数f(i)的值作为BP 神经网络的输入，更新网络中各层参数的计算值，其中输出即为Backstepping控制器的增益K。

（4）根据式（22）计算输出速度。

（5）进行神经网络学习，不断调整权系数，将损失函数值梯度下降到局部最优解，从而实现对Backstepping控制器增益的自适应调节。

（6）返回第（2）步。

3.3 稳定性分析

定理1移动机器人在Backstepping运动学控制器、BP 神经网络增益自整定控制器的共同作用下，所设计的TEMC控制系统是渐进稳定的。

证明对于式（19）所描述的全局Lyapunov 函数，可以看出V2≥0，当且仅当(,ye,θe)T=0 时，V2=0。将所设计的控制率式（22）代入式（21）中得：

综上，在控制率式（22）及自整定控制增益K的作用下，位姿误差d=[xe ye θe]T是渐进稳定的，能达到的目的，即能在有限时间内控制机器人收敛于期望轨迹。

4 仿真与实验

为了验证移动机器人在室内建筑施工中的有效性以及上述路径评价模型和路径评价函数的可行性，实验采用分段函数和双扭线作为参考轨迹，取跟踪误差和横摆误差θe来分析控制器的性能，并与传统反演法控制器（TIC）[17]及自适应反演法控制器（AIC）[18]进行对比，同时采用误差的均方根Xrms(Le)、Xrms(θe)和最大误差Emax(Le)、Emax(θe)来评估各个控制器的性能。实验中，移动机器人底盘的长L=0.183 m、宽W=0.132 m、车轮半径R=0.037 5 m，取离散化采样时间间隔Δt=0.01 s，考虑到移动机器人主要工作在室内低速场景，在实验中采用恒定且较低的期望速度μr=0.5 m/s。

4.1 仿真实验

在仿真实验中，TEMC 控制器的各个参数选取如表1所示。

表1 TEMC参数选取（仿真）Table 1 TEMC parameter selection（simulation）

4.1.1 轨迹跟踪实验

实验1分段轨迹跟踪实验：采用直线Xd=-2π 与正弦曲线Xd=t,Yd=-5 sin(t/2)的组合作为参考轨迹。参考轨迹的初始位姿为Q=[-2π-13 π/2]T，实际起始位姿为Qr=[-2π-1-14 3π/20]T。同时，用于路径复杂度评价的路况特征点数量n=30。实验结果如图6所示，实验数据如表2所示。

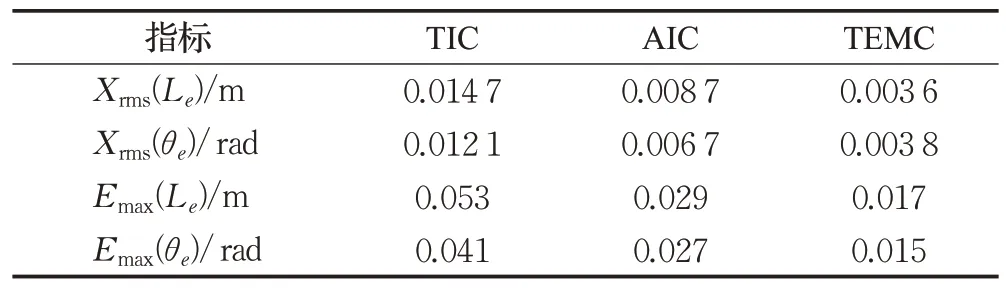
表2 分段轨迹评价指标（仿真）Table 2 Segmented trajectory evaluation index（simulation）

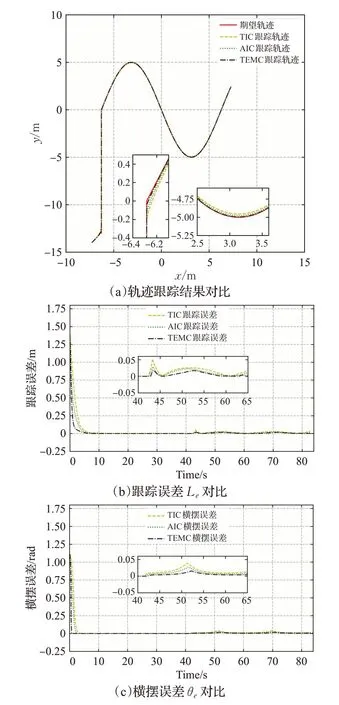
图6 分段轨迹结果对比（仿真）Fig.6 Comparison of segmented trajectory results（simulation）

实验1 结果分析：在参考轨迹中，直线轨迹和正弦轨迹的衔接处存在路径曲率及曲率变化率突变的情况。在衔接处，TIC和AIC的跟踪曲线出现了明显的跟踪误差，而TEMC 在曲线衔接处能快速适应，其跟踪曲线无剧烈波动且响应速度高。在正弦轨迹的上凹处，参考轨迹曲率发生了快速波动，TIC和AIC出现了没有跟踪上的情况，轨迹跟踪误差较大，而TEMC 跟踪效果良好。实验1验证了上文所提出路径评价机制的可行性，将路径评价模型引入到轨迹跟踪控制器中能有效地提高跟踪精度，同时能够适应曲率变化率突变的路况，在曲率波动较大的轨迹上也能快速且准确地跟踪。

实验2双扭线轨迹跟踪实验。采用双扭线作为参考轨迹，其表达式为Xd=5 cos(πt/15),Yd=-5 sin(2πt/15)。参考轨迹的初始位姿为Q=[5 0 π/2]T，实际起始位姿为Qr=[-3-1 3π/20]T。同时，用于路径复杂度评价的路况特征点数量n=30。实验结果如图7 所示，实验数据如表3所示。

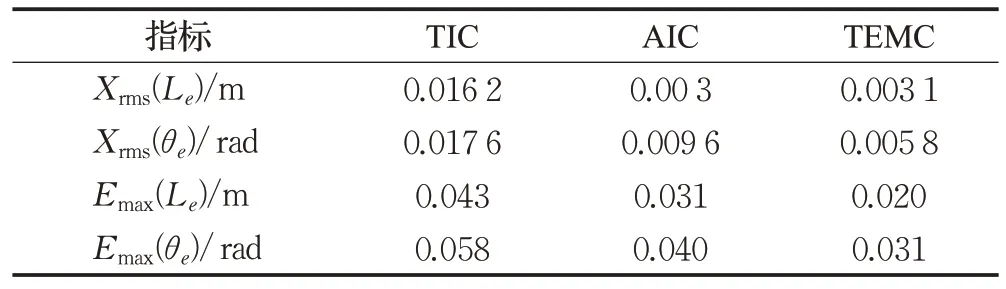
表3 双扭线轨迹评价指标（仿真）Table 3 Double helix trajectory evaluation index（simulation）

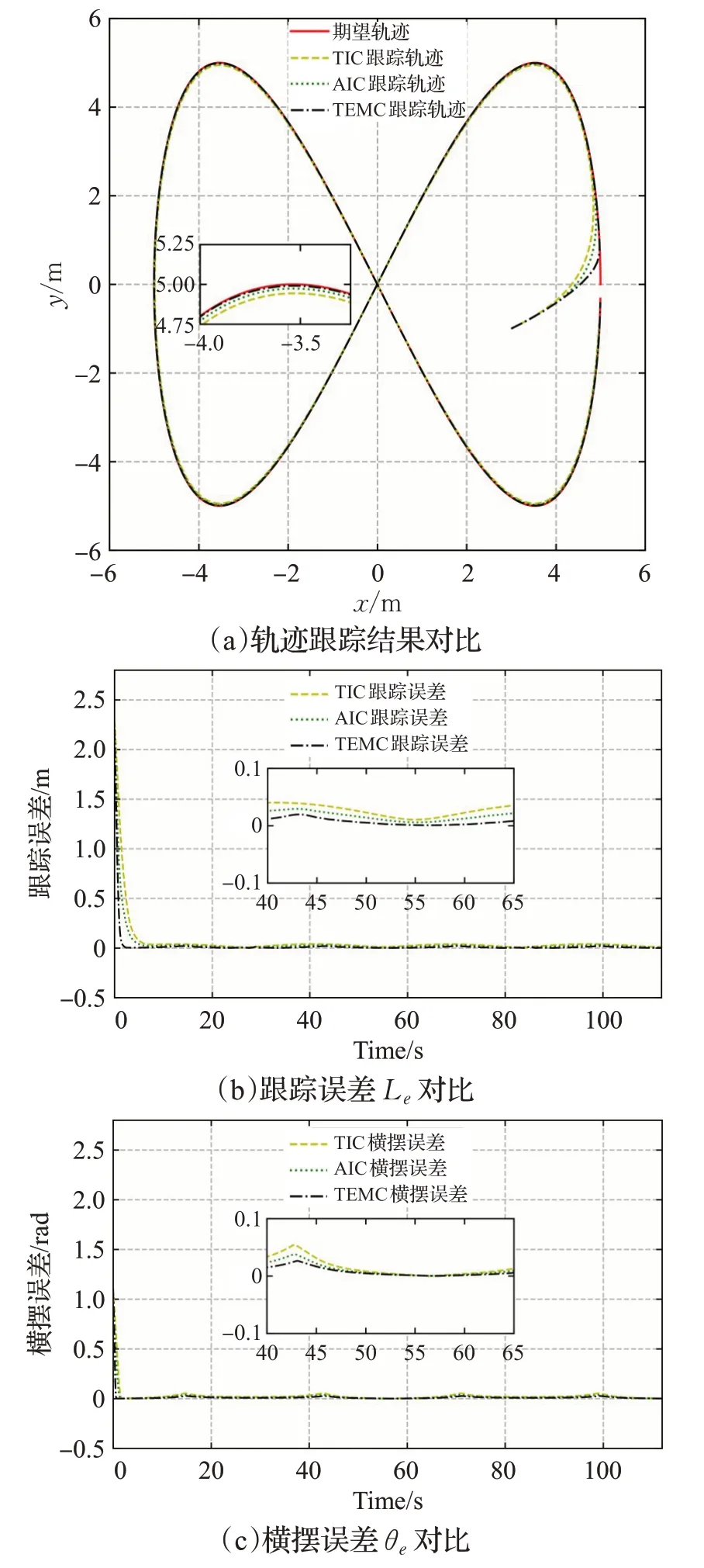
图7 双扭线实验结果对比（仿真）Fig.7 Comparison of double helix trajectory results（simulation）

实验2结果分析：参考轨迹双扭线上的曲率及其变化率波动更加明显，也能更好地测试各控制器的跟踪性能。在起始位姿误差存在的情况下，TEMC控制器的收敛速度要快于TIC 和AIC 控制器。由于TEMC 控制器引入了路径评价机制，对于理论轨迹曲率变化较大的路段，TEMC 控制器能进行快速稳定地跟踪，且跟踪误差无明显震荡现象。而TIC 和AIC 控制器主要考虑自身的位姿误差，无法对理论轨迹的复杂度进行分析，对于曲率及其变化率波动较大的路段不能进行较好地跟踪，跟踪误差较大。实验2 进一步论证了针对复杂轨迹的跟踪，考虑未来路径曲率对控制决策的影响，将有效提高移动机器人的跟踪精度。

4.1.2 路径评价函数权值系数η 选取实验

由人类驾驶员驾驶汽车的经验可知，如何操控汽车平稳地驾驶取决于前方道路的弯曲程度，例如当汽车行驶在崎岖的道路上时，通常需要提前调整汽车的位姿，以便顺利地切入每一个急弯。同时由式（4）以及TEMC系统结构可知，权值系数η的选取将直接影响路径评价函数对路径曲率froad(i)及车辆跟踪误差fvehicle(i)重要性评估的侧重点，从而间接影响轨迹跟踪的性能。针对不同的应用场景如何选取合适的权值系数，将通过对比实验进行说明。

为了初步评估整体理论跟踪轨迹，在式（5）及式（6）的基础上，定义整体路径复杂度的概念，表示如下：

实验3分别采用上文中的分段轨迹和双扭线轨迹作为实验对象，其中分段轨迹的整体路径复杂度Ψsegment=0.602 3，双扭线轨迹的整体路径复杂度Ψtwist=0.828 2，实验过程中通过调整权值系数η的取值，观察误差值，找出权值系数η与整体路径复杂度Ψ之间的关系。实验结果如图8、图9所示，实验数据如表4、表5所示。

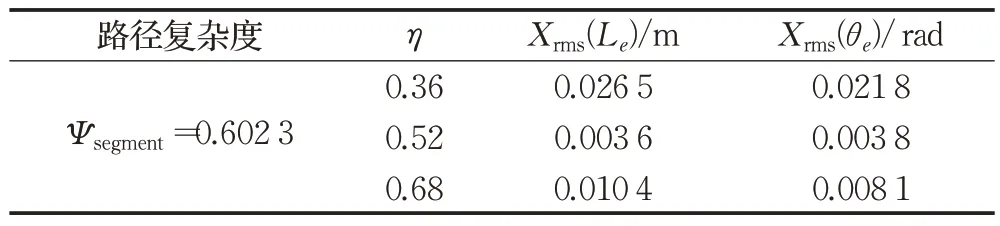
表4 分段轨迹评价指标（仿真）Table 4 Segmented trajectory evaluation index（simulation）

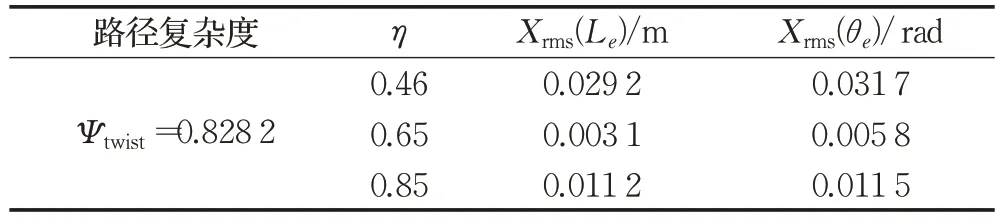
表5 双扭线轨迹评价指标（仿真）Table 5 Double helix trajectory evaluation index（simulation）

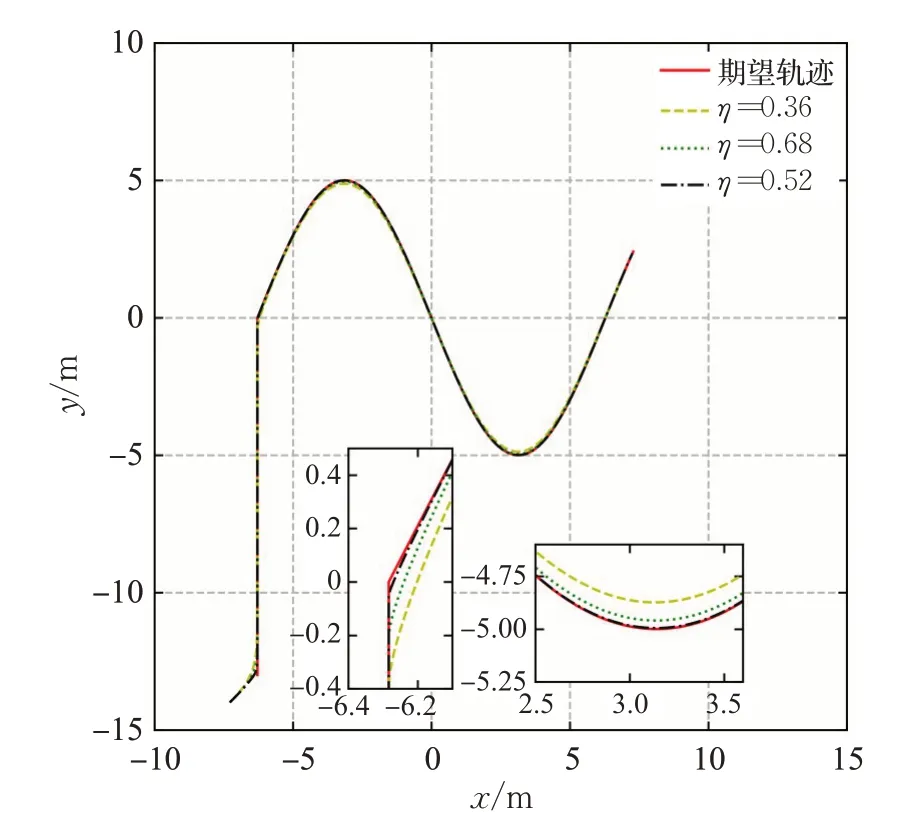
图8 分段轨迹η 的敏感性分析（仿真）Fig.8 Sensitivity analysis of segmented trajectory η（simulation）

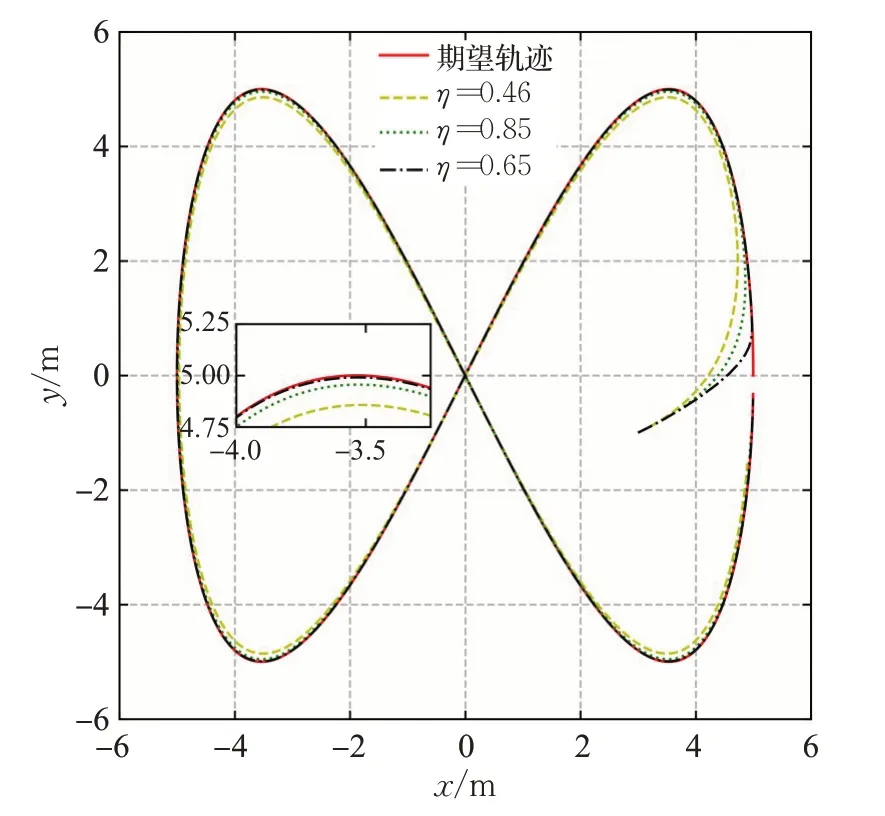
图9 双扭线轨迹η 的敏感性分析（仿真）Fig.9 Sensitivity analysis of double helix trajectory η（simulation）

实验3结果分析：首先通过大量的对比实验找出了对应于两段不同复杂度轨迹的最优η值，分别为η=0.52和η=0.65。在此基础上，分别将η值增大和缩小30%。实验结果表明，针对同一轨迹在一定范围内，η值越大跟踪效果越好，但η值过大将降低车辆跟踪误差fvehicle(i)的权重，从而导致跟踪误差增大的情况。经过实验分析，η的取值不宜大于70%，并且针对整体路径复杂度不同的情况，复杂度越大，η的取值越大。

4.2 实物实验

为了进一步分析上述路径评价模型和路径评价函数的可行性，将上述控制方法应用于自主搭建的麦克纳姆轮移动机器人中。其上位机基于ROS 操作系统开发，运行在Ubuntu 18.04 上，核心算法功能包均采用C++/Python 进行编写，下位机核心代码基于C 语言开发。机器人系统框架如图10所示。

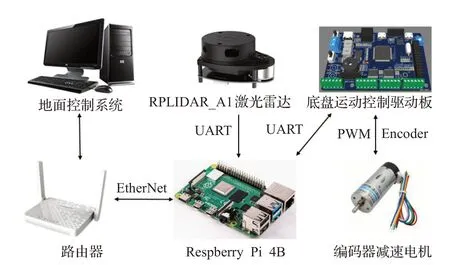
图10 机器人系统框架Fig.10 Robot system framework

其中，底盘运动控制板为基于STM32的驱动板，集成了4 路直流电机驱动、MPU9250 陀螺仪、蓝牙以及OLED 等模块，同时可以实现串口和CAN 通信。ROS平台运行在Raspberry_Pi 4B 上，主要承担着激光雷达信息的处理、轨迹跟踪控制器的运行以及与STM32 控制命令的交互。实物机器人的具体结构如图11 所示，控制器的各个参数选取如表6所示。

表6 TEMC参数选取（实验）Table 6 TEMC parameter selection（experiment）

图11 机器人实物图Fig.11 Actual diagram of robot

实验结果分析：从图12以及表7的实验结果可以看出，针对双扭线这类跟踪轨迹曲率及曲率变化率较大的参考轨迹，基于路径评价模型设计的TEMC控制器跟踪效果明显优于TIC和AIC控制器。同时，实物实验也进一步证明了前文所设计的路径评价模型的可行性与先进性，论证了考虑未来路径信息对控制决策的影响将有效提升移动机器人跟踪精度，且机器人跟踪精度满足建筑施工的作业要求。

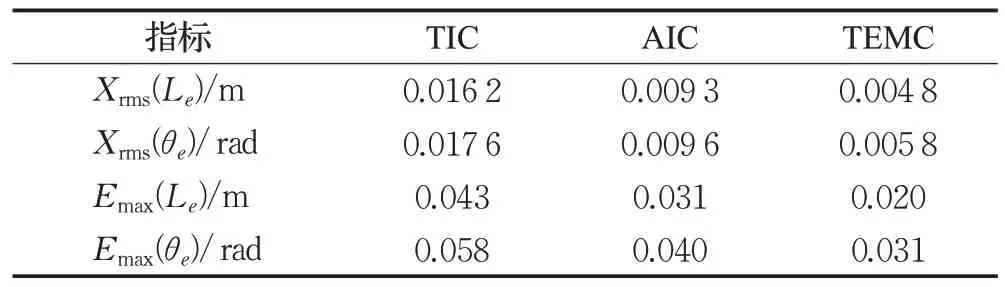
表7 双扭线轨迹评价指标（实验）Table 7 Double helix trajectory evaluation index（experiment）

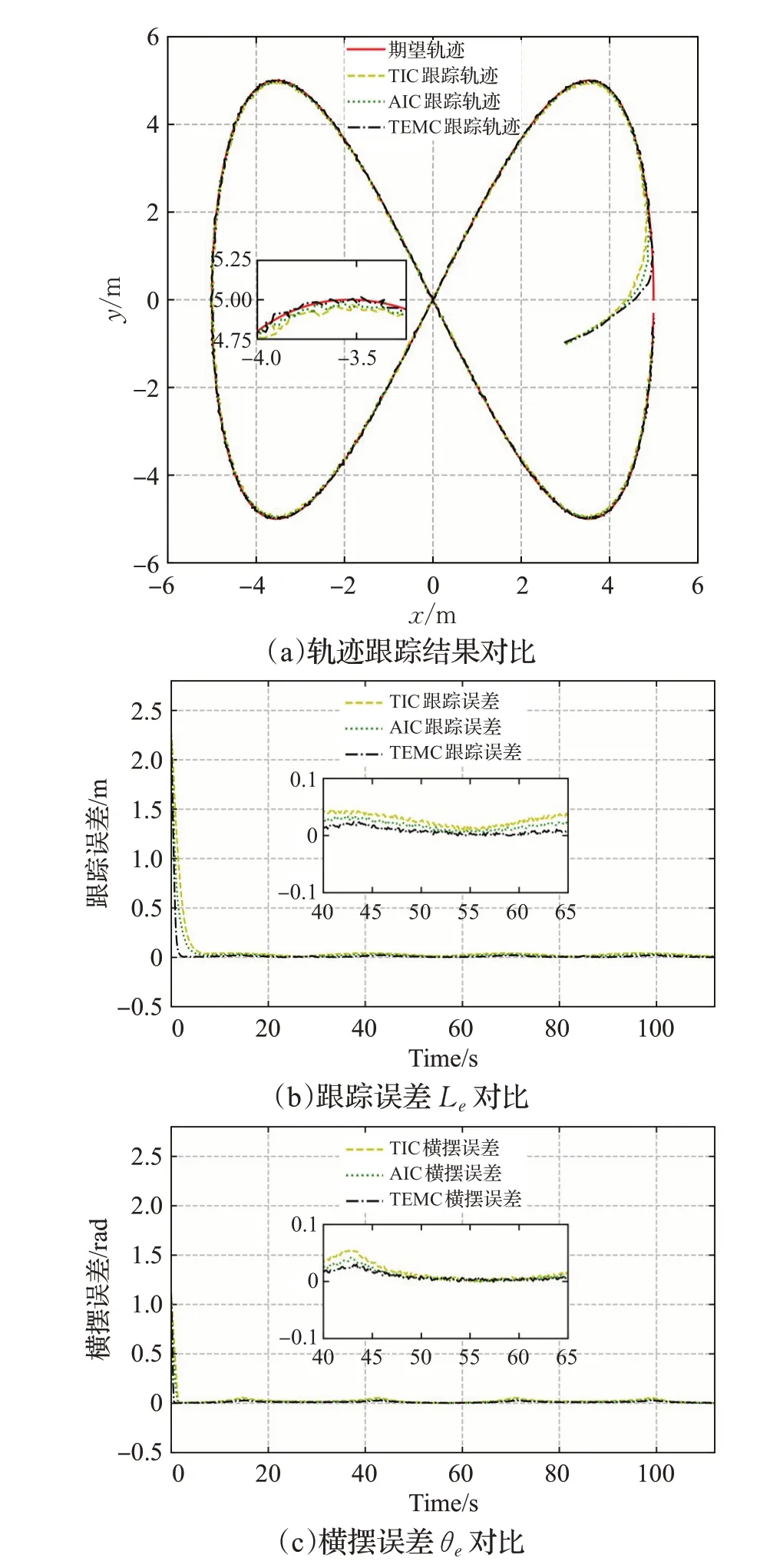
图12 双扭线实验结果对比（实验）Fig.12 Comparison of double helix trajectory experimental results（experiment）

5 结论

针对现有轨迹跟踪控制器主要考虑自身的位姿误差，未考虑路径曲率对跟踪控制的影响，将路径曲率引入到轨迹跟踪控制当中，提出了一种基于路径评价模型的跟踪控制方法。首先，针对机器人运动学模型和位姿误差模型进行分析；其次，建立了一种路径评价模型，并提出了一种路径评价函数，该函数能对未来一定时间内的路径曲率和车辆跟踪误差进行综合分析；然后，为了验证上述路径评价模型的可行性，基于Backstepping 方法设计了一种参数自整定控制器，并证明了该控制器是渐近稳定的；然后，通过实验法给出了路径评价模型中关键参数的合理取值范围；最后，通过仿真及实物实验进一步论证了未来路径曲率会对控制决策产生影响，将路径评价模型引入到控制系统中能有效提高轨迹跟踪的精度。在实物对比实验中，TEMC控制方法与其他前馈控制器相比，轨迹跟踪精度提升了48%以上。