基于神经网络的废物桶活度测量方法研究

舒旻翔 单陈瑜 顾卫国 王德忠

1（上海交通大学 国家电投智慧能源创新学院 上海 200240）

2（中广核研究院有限公司 深圳 518031）

3（上海交通大学 机械与动力工程学院 上海 200240）

核电厂在运行的过程中，会产生大量的放射性固体废物［1］，其中95%以上是低、中水平放射性固体废物（简称低中放固废）［2］。这些低中放固废经固化或压缩后，被整备成200 L、400 L废物桶［2］。由于放射性固体废物的特殊性，其妥善管理和安全处置是核电厂运营单位高度重视的问题。根据放射性废物管理规定［3］，固体废物应按其放射性活度和所含核素半衰期的不同分类贮存。因此，放射性固体废物最终处置前，必须检测其所含放射性核素的种类与活度。

目前，无损测量技术（Non-Destructive Assay，NDA）已广泛应用于核电厂的桶装废物核素的识别与活度测量［4］，主要包括分段γ 扫描（Segmented Gamma Scanning，SGS）与层析γ 扫描（Tomographic Gamma Scanning，TGS）。SGS将废物桶分为多个段层，假设每个段层内介质与核素均分布均匀，因此当段层内介质或核素不均匀分布时会导致严重的测量误差［5］。TGS 将每个断层划分为多个体素，对每个体素进行密度重建和活度重建，可以对介质和核素非均匀分布的废物桶进行测量，提高了测量的精度［6］。然而，其较多的测量次数导致其测量时间较长，限制了其在工业上的应用。为了提高测量精度，刘诚等提出了改进型分段γ 扫描技术［7-8］，该方法将介质均匀分布的废物桶里的点源等效为环源，通过两个不同位置的探测器的计数率比值得到等效环源的半径，最终实现准确的活度重建。该方法的测量精度较传统SGS 有较大提高，但是需要进行大量计算来确定合适的测量位置。

近些年随着人工智能的迅速发展，神经网络等方法也开始被应用到各个方面。有学者［9-10］利用卷积神经网络来完成TGS透射测量图像的重建，利用低分辨率的原始图像得到了高分辨率图像，减少了透射测量的次数，缩短了透射测量的总时间。也有学者利用神经网络来实现γ能谱的解析［11-12］，实现了核素种类的快速识别，且精度高于传统方法。韩国学者Kim 等［13］将机器学习用于放射源的定位，利用两个光子计数器和塑料闪烁光纤实现了放射源的一维定位，可以快速找到废物桶表面的泄漏处。Bae等［14］使用NaI 探测器在平面上进行扫描，利用神经网络实现了平面上放射源的定位（无介质）。由于废物桶内的介质会对核素衰变产生的光子产生影响，且废物桶内核素数量未知，因此上述放射源定位方法无法直接应用于废物桶的测量。

针对以上问题，本文将神经网络技术与改进型分段γ 扫描技术相结合，实现废物桶等效环源位置的快速确定，最终实现准确的活度重建。该方法简单、快速，弥补了传统方法的不足。

1 方法与原理

沿着废物桶轴向将废物桶分为多个段层。对于介质均匀分布的废物桶，由于其匀速旋转，因此桶内某半径上的点源可以被等效为该半径处的环形线源［7-8，15］。

假设某一断层内有N个位于不同半径的同一种类的点源，其可以等效为N个不同半径的环源。对该断层进行测量时，对于核素衰变发射的能量为e的γ射线，探测器的计数率为：

式中：α为核素发生衰变时发射该能量的γ射线的概率；An为第n个核素的活度；En为探测器对第n个核素发射出的能量为e的γ 射线的探测效率。假设该断层内该种核素总活度为A，第n个核素的活度An与总活度A的比值为εn，则探测器的计数率可以表示为：

对En进行加权平均，权重分别为εn，结果为E'。则式（2）可以表示为：

由于En随着环源半径r连续，因此存在半径r'使得探测器对该处环源的探测效率为E'。此时，该断层内所有环源等效为一个环源，该等效环源的活度与所有环源的活度之和相等。假设确定了等效环源的半径r'，即可通过探测效率E'和计数率C计算得到该断层内某种核素的总活度A，将每一断层求得的活度相加，即可得到废物桶内该种核素的总活度。

废物桶测量过程中，可以直接获得探测器的计数率C。由式（3）可知，对某一层进行测量时，探测器计数率C与该层内某一核素的总活度A、等效环源半径r'有关。由于总活度A未知，因此，无法直接根据计数率C得到等效环源半径r'。

如图2 所示，假设探测器在位置A 和B 对某一断层进行测量，计数率分别为CA、CB。根据式（3）有［15］：

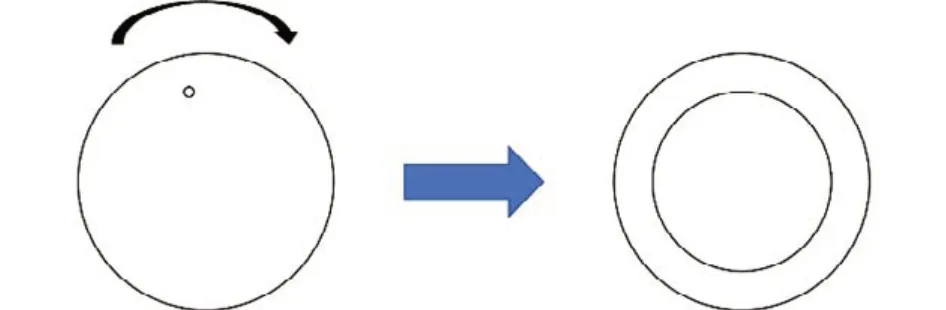
图1 点源等效为环源Fig.1 Schematic diagram of point source equivalent to ring source

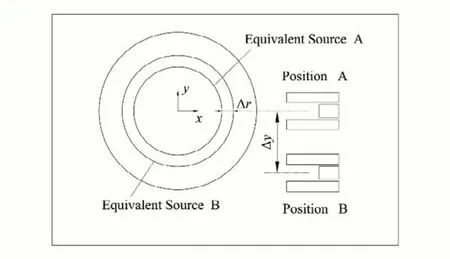
图2 测量位置示意图Fig.2 Diagram of measuring position

式中：rA为探测器在位置A 时的等效环源半径；rA+Δr为探测器在位置B 时的等效环源半径。从式（4）可知，不同位置的探测器的计数率比值仅与等效环源的半径有关而与活度无关。不同位置的探测器的计数率比值与等效环源半径存在函数关系该函数关系十分复杂，难以直接计算获得。

人工智能是目前最广泛使用的用于确定各种参数之间未知和复杂关系的技术之一［16-18］。本文利用神经网络技术建立以多个不同测量位置的探测器的计数率比值作为输入，等效环源的半径作为输出的模型，利用大量的数据集对神经网络模型进行训练，建立输入和输出之间的映射关系。从而准确、快速输出等效环源的半径，最终实现准确的活度重建。

2 神经网络模型

2.1 数据集的获取

本文通过模拟测量来获得不同测量位置的探测器的计数率。由于蒙特卡罗方法计算时间长，本文利用数值计算方法来进行废物桶的模拟测量［8］。

计算探测器对不同半径的环源的探测效率时，将环形线源离散为该半径上不同角度的多个点源，分别计算点源位于不同角度时的探测效率。由于环源是由点源旋转等效而来，且旋转速度恒定，因此环形线源的活度随角度均匀分布，对同一半径不同角度的点源对应的探测效率进行平均即可得到探测器对该半径处的环源的探测效率。

分别按照不同的点源角度增加步长计算探测器对环形线源的探测效率，探测器采用美国ORTEC公司生产的高纯锗探测器，其尺寸参数如表1 所示。如图3、4所示，准直口大小为20 cm×9 cm，铁层宽度为1 cm，铅层宽度为8 cm，准直器整体厚度为25 cm。废物桶为核电厂常用的400 L 桶，由于水泥固化是核电厂常用的固体废物处理手段之一，因此桶内介质设置为混凝土（密度2.3 g·cm-3），探测器正对废物桶，放射源为Co-60，其衰变产生的γ 射线能量为1.332 5 MeV，发射光子数目为108，源与探测器中心处于同一高度。结果如图5、6所示。

图3 准直器示意图Fig.3 Schematic diagram of collimator

图4 测量系统示意图Fig.4 Schematic diagram of measurement system

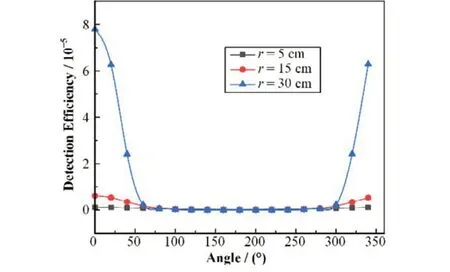
图5 步长为20º时，探测器对不同角度点源的探测效率Fig.5 Detection efficiency of point sources at different angles when step is 20°

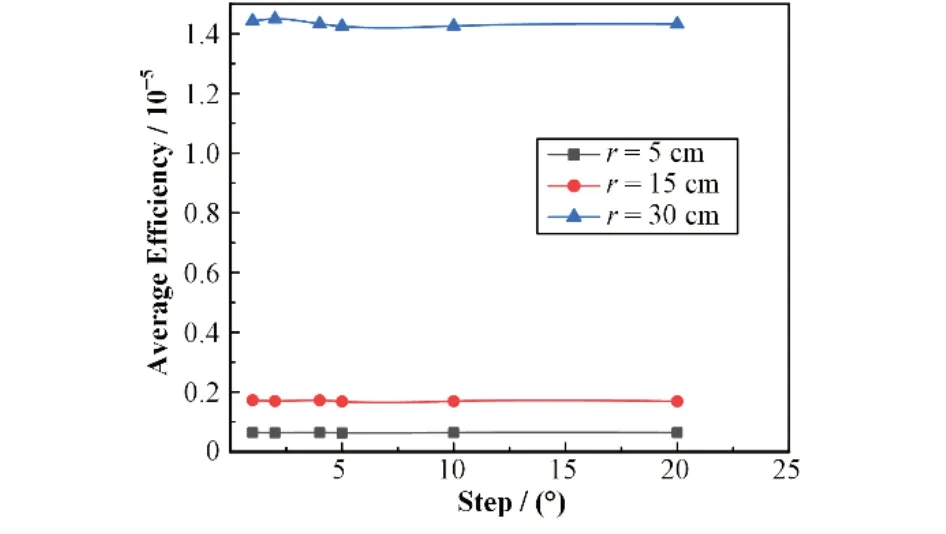
图6 不同步长下的探测效率Fig.6 Detection efficiency at different steps

表1 探头尺寸参数Table 1 Probe size parameters

假设点源角度增加步长为1°时的探测效率为E1，步长为j时的探测效率为Ej（j=2º， 4º， 5º， 10º，20º），相对误差δ为：

点源位于不同半径，不同角度增加步长下的相对误差δ如表2所示。

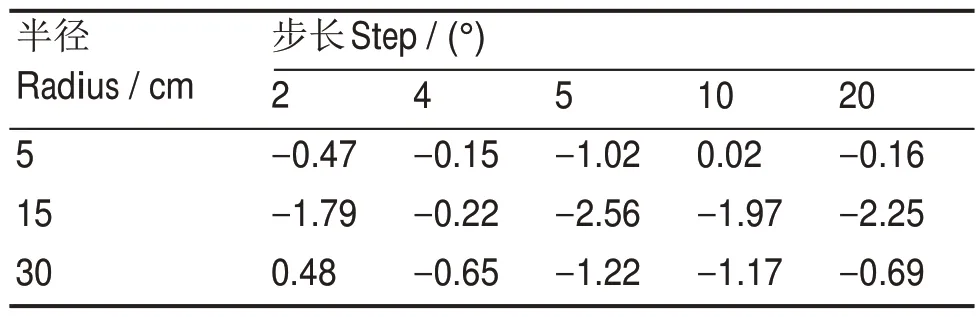
表2 不同步长下的相对误差(%)Table 2 Relative error at different steps (%)

可以看到，用探测器对某半径处不同角度点源的探测效率的平均值来表示探测器对该半径处环形线源的探测效率时，所选择的点源间的不同角度步长对计算结果基本没有影响。步长为2°、4°、5°、10°和20°对应的探测效率计算结果与步长为1°的探测效率计算结果相对误差均在±3%以内。因此，为了减小计算量，可以分别计算出探测器对某半径上均匀分布的18 个点源（每两者间隔20°）的探测效率，再将其平均便可得到探测器对该半径处的环形线源的探测效率。

本文利用多个测量位置的探测器的计数率比值来确定等效环源的半径。因此，需要分别计算环源位于不同半径时，不同测量位置的探测器的计数率。计算工况与上文相同，结果如表3所示。其中y表示探测器的偏移距离。

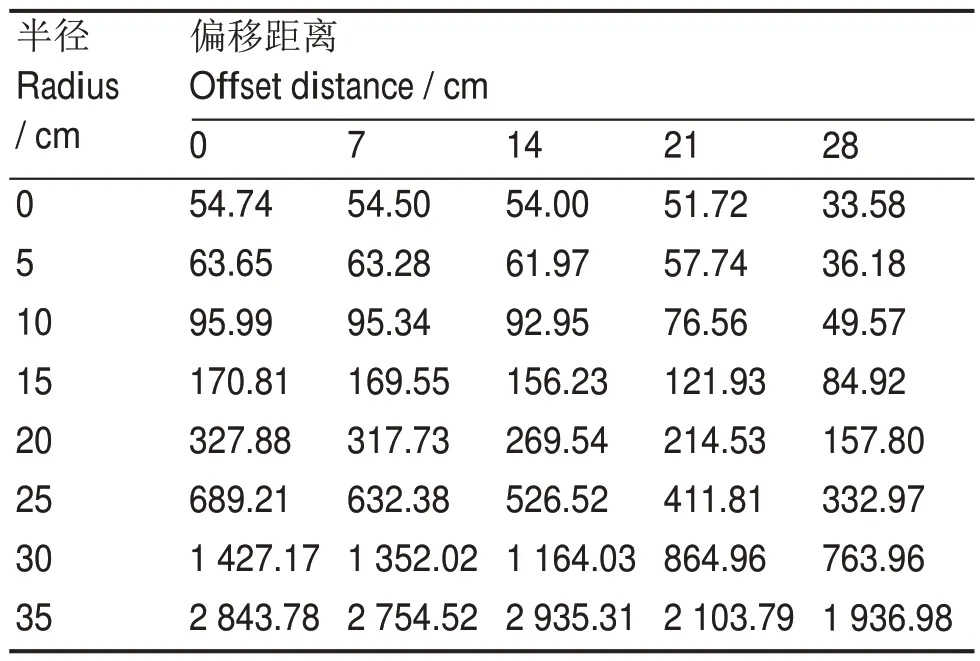
表3 不同测量位置的探测器的计数率计算结果Table 3 Count rate for detectors at different measurement positions

为了得到不同半径环源下的探测器的计数率，对表3 中的计算结果进行三次样条插值，得到不同半径环源下不同测量位置的探测器的计数率。结果如图7所示。其中图7（a）为利用三次样条插值得到的结果，图7（b）为根据数值计算得到的结果。

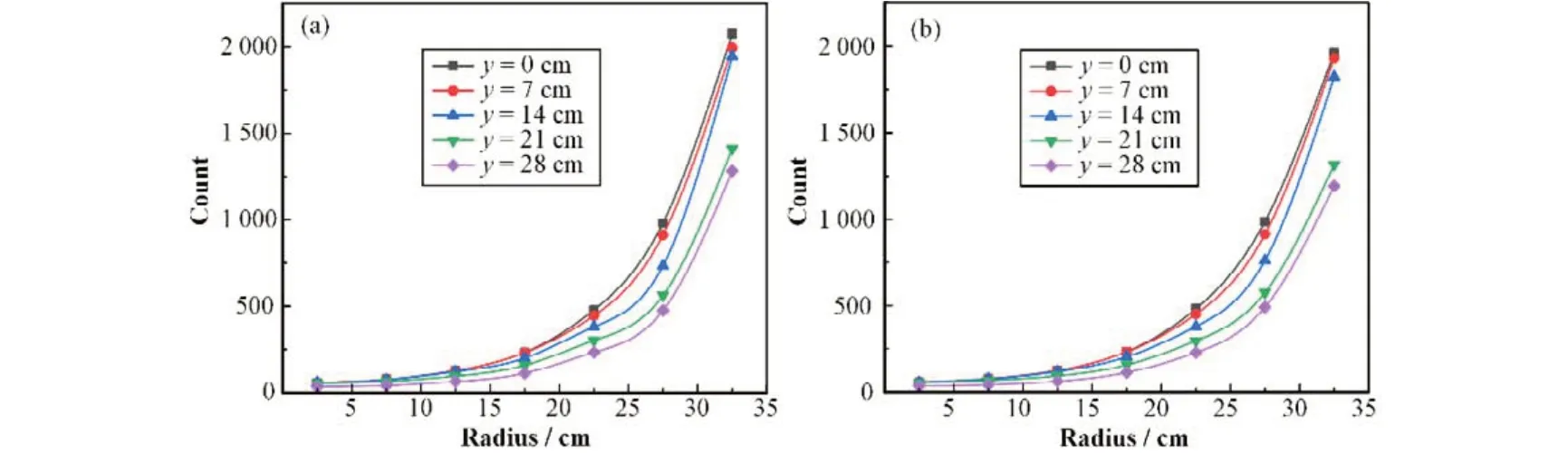
图7 计数率结果 (a) 插值结果，(b) 数值计算结果Fig.7 Results of count rate (a) Interpolation, (b) Numeral calculation

假设插值的计数率结果为Cint，数值计算的结果为Ccal，相对误差为：

不同环源半径下计数率的相对误差结果见表4。

表4 计数率插值与数值计算结果相对误差(%)Table 4 Relative error of count rate between interpolation and numerical calculation (%)

表5 单源活度重建结果Table 5 Activity reconstruction results of single source

可以看出，当环源半径小于等于27.5 cm 时，计数率插值结果与数值计算结果相对误差均小于±4%。当源靠近废物桶边缘时，计数率插值结果与数值计算结果相对误差增大，但仍小于8%。因此，可以利用三次样条插值来获得源在不同半径时不同测量位置的探测器的计数率。

2.2 神经网络模型

假设每个测量位置的探测器的计数率为Ci（i=0，1，2，…），所有计数率的平均值为C，定义相对计数率比值：

将相对计数率比值ai作为神经网络的输入。等效环源半径r'作为神经网络的输出。

本文使用误差反向传播（Back Propagation，BP）神经网络，迭代算法为梯度下降法，输入层神经元数量与探测器数量相等，均为3，隐层数量为2，每层隐层的神经元数目为8，激活函数为tanh函数，学习率为0.5，迭代次数为10 万，输出层神经元数量为1。神经网络模型用Python3.7搭建，神经网络训练过程如图8所示。

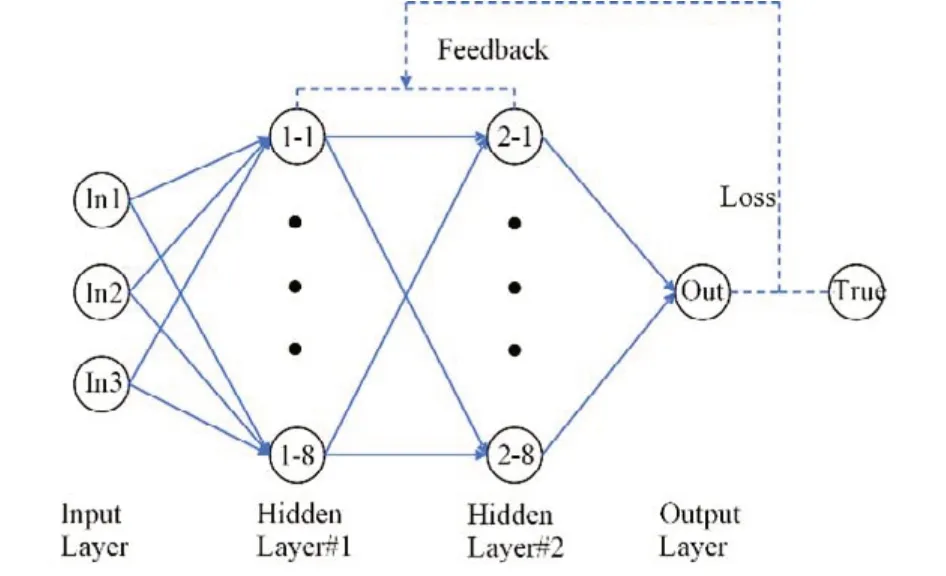
图8 神经网络训练过程示意图Fig.8 Diagram of neural network training process

神经网络的数据集分为两部分：训练集和测试集。通过三次样条插值得到0～35 cm 内的500 组不同半径的Co-60环源所对应的不同测量位置的探测器的计数率，将对应的相对计数率比值和环源半径作为训练集。再随机生成50个不同半径的Co-60环源，将其对应的相对计数率比值和环源半径作为测试集。

假设训练集中环源的真实半径分别为ri（i=1，2，…，500），每轮迭代后神经网络输出的环源预测半径分别为rj（j=1，2，…，500）。每轮迭代后环源半径的预测值与真实值的平均绝对误差（Mean Absolute Error，MAE），即神经网络的损失函数为：

每轮迭代后的loss_r 结果如图9 所示。迭代10万轮后，loss_r 已经收敛，说明神经网络已经完成训练。

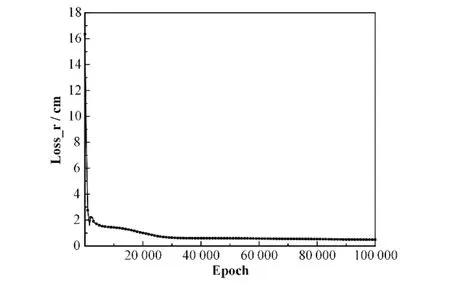
图9 100 000轮迭代后的损失函数Fig.9 Loss function after 100 000 iterations

神经网络训练完成后，便可根据测试集中各个相对计数率比值直接预测等效环源半径，最终实现核素的活度重建。神经网络预测过程如图10所示，活度重建过程如图11所示。

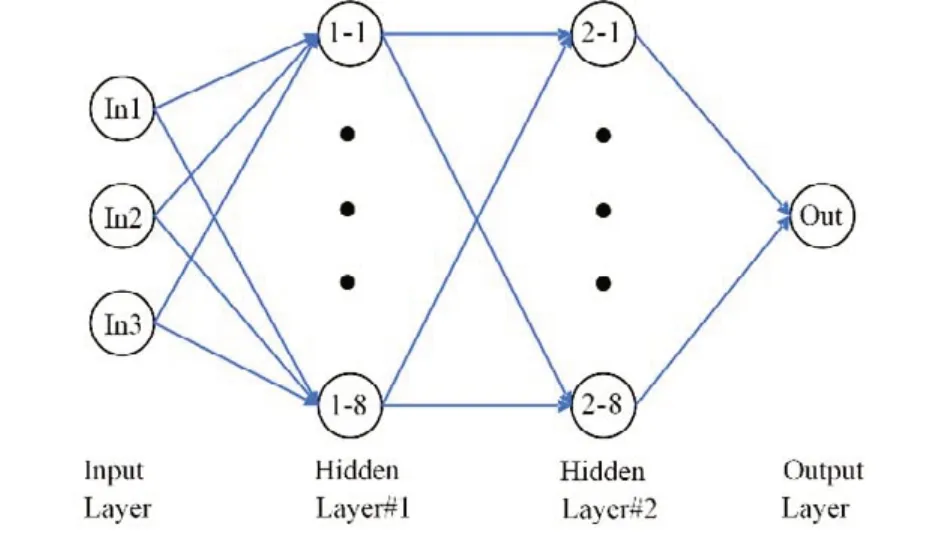
图10 神经网络测试过程示意图Fig.10 Diagram of neural network testing proces

图11 基于神经网络的废物桶活度重建过程示意图Fig.11 Process diagram of activity reconstruction of waste drum based on neural network

3 结果与分析

3.1 单环源的结果

当断层内只有一个点源或者多个点源位于同一半径时，此时只有一个环源，等效环源半径即为环源半径。图12 为将3 个不同测量位置的探测器（偏移距离分别为0 cm、21 cm、28 cm）的相对计数率比值作为输入时，神经网络的预测结果。其中，横轴rt表示环源的真实半径，纵轴rp表示预测半径。

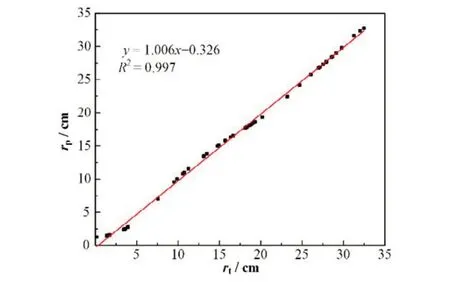
图12 环源半径的预测值与真实值Fig.12 Predicted and true radii of ring source

环源半径预测值与真实值的绝对误差为：

测试集中50 组环源半径的预测值与真实值平均绝对误差为0.429 cm，最大值为1.175 cm，均方根误差（Root Mean Square Error，RMSE）为0.536 cm，其计算公式为：

对测试集中环源半径的预测值与真实值进行线性拟合，拟合直线斜率为1.006，相关系数为0.997，说明预测值与真实值有着良好的线性关系，神经网络可以准确预测等效环源的半径。

利用神经网络预测得到等效环源的半径后，根据式（12）可重建出源的活度。其中，Ap为环源的活度重建值；C为探测器的计数率；α为核素衰变发射出该能量的γ 射线的概率；Ep表示源的半径为rp时，探测器的探测效率。

测试集中50 组环源的活度重建结果见图13。由图13 可知，当源靠近废物桶的中间区域（r=20 cm）时，活度的重建值与真实值相对误差较大；对于靠近废物桶中心（r=0 cm）和边缘（r=35 cm）的源，活度重建值的误差较小。计算50 组环源的活度重建值与真实值的相对误差，其平均值为4.26%，最大值为12.63%，标准差为5.28%。

图13 单环源活度重建结果Fig.13 Activity reconstruction value of single ring source

3.2 多环源的结果

当废物桶内存在多个环源时，相比于单环源情况，此时每个探测器的等效环源不一定重合，由于神经网络只输出一个值，因此等效环源的预测值与真实值会产生更大的误差，导致活度重建的误差增大。由于实际测量过程中废物桶内源数量未知，因此，必须计算废物桶内存在多个环源时，活度重建结果的误差。

为了模拟多环源的情况，将测试集中的50个环源随机分为10 组，每组包含5 个环源。分别计算每组5个环源活度相等时，3个不同测量位置的探测器（偏移距离分别为0 cm、21 cm、28 cm）的相对计数率比值。将其作为输入，利用神经网络输出等效环源的半径r。计算环源半径为r时各探测器的探测效率Er，代入式（12）即可计算出等效环源的活度Ae。

10 组多环源的活度重建结果见图14。10 组活度重建结果的平均相对误差（Mean Relative Error，MRE）为24.27%，最大值为42.41%，标准差为26.53%。由于多个环源存在时三个探测器的等效环源不再重合，因此神经网络预测等效环源半径偏大，导致探测效率偏大，代入式（12），活度重建值偏小。

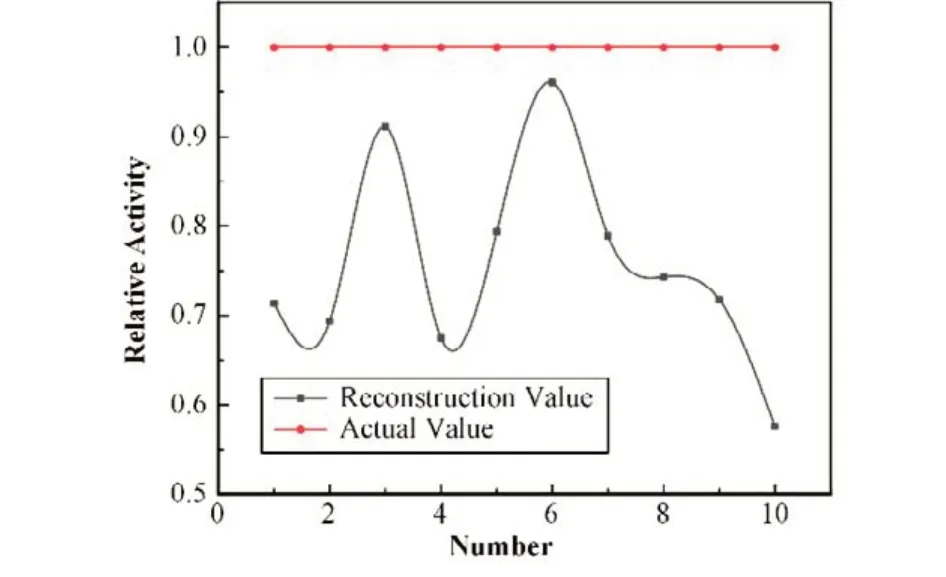
图14 多个源活度重建结果Fig.14 Reconstructed value of total activity from multiple sources

3.3 传统测量方法的结果

利用传统的测量方法进行废物桶的活度重建，将基于传统测量方法的结果与新方法的结果对比，验证新方法的可靠性。

首先利用分段γ扫描方法SGS进行废物桶的测量。SGS 需先确定每层的高度以计算探测效率Es。根据§2.1 的准直器开口和测量距离，层高设置为12 cm。

探测器正对废物桶，其他条件与§2.1 相同。将探测器探测效率Es和计数率Cs代入式（12）即可得到源活度的重建值Ar。对测试集中50 组单环源进行活度重建，结果见图15（a）。由于SGS 假设源在介质内均匀分布，因此当环源靠近废物桶中心时，探测效率计算值偏大，导致活度重建值偏小；当环源靠近废物桶边缘时，探测效率计算值偏小，导致活度重建值偏大。

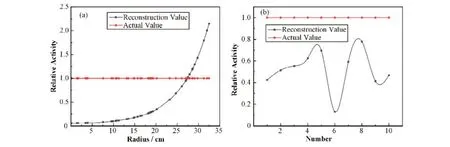
图15 SGS活度重建结果 (a) 单环源，(b) 多环源Fig.15 Activity reconstruction value of SGS (a) Single source, (b) Multi-sources

50 组单环源活度重建值与真实值的相对误差平均值为68.15%，最大值为114.54%，标准差为74.56%。

分别将§3.2中10组多环源对应的偏移距离为0的探测器的计数率和探测效率代入式（12）进行活度重建，10 组多环源的活度重建结果见图15（b）。计算10组多环源总活度重建值与真实值的相对误差，其平均值为48.02%，最大值为86.96%，标准差为50.95%。从图15（a）可知，源环半径接近27 cm时探测效率与SGS假设的体源探测效率相等，而10组多环源下的环源平均半径均小于27 cm，导致探测效率值偏大，活度重建值偏小。

利用测量精度更高的层析γ扫描方法TGS进行废物桶的测量。由于本文对均匀废物桶进行研究，因此本文采用两种网格划分方式，第一种为传统TGS，在废物桶径向和周向进行划分，此时点源不再等效为环源；第二种只在废物桶的径向上进行划分，该种划分方式对应的扫描方法也称为半层析扫描（Semi-tomographic Gamma Scanning，STGS）［19-20］。此时点源等效为环源。

按TGS 进行网格划分时，沿着废物桶径向划分5次；沿着废物桶周向划分12次；废物桶每个断层被划分为60 个网格。探测器在周向上有12 个测量位置；在偏移方向有5个测量位置；每次TGS探测器一共进行60 次测量。按STGS 进行网格划分时，只需沿着废物桶径向划分，分别将废物桶每个断层划分为3个和5个网格。

分别利用数值计算方法得到探测器的探测效率矩阵E与计数率向量C，其中工况设置与§2.1 相同。代入式（13），其中Eij（i，j=0，1，…，n）表示探测器位于第i个探测位置，放射源位于第j个网格的几何中心时探测器的探测效率。Ci（i=0，1，…，n）表示源位于测试集中环源半径的真实值rt时，探测器在每个测量位置时的计数率。n为网格数量。

本文采用极大似然期望最大化算法（Maximum Likelihood Expectation Maximization，MLEM）对公式（13）求解［21］，其迭代公式为：

其中：Aj（k+1）为第k次迭代时，第j个网格的活度求解值；Ei为探测效率矩阵E的第i行；A（k）为活度向量A第k次迭代时的结果。

利用式（13）、（14）解得每个网格的活度值Aj，将所有网格的活度重建值求和即可得到总活度。

根据TGS 进行测量与活度重建的结果如图17所示。50 组单点源活度重建结果的平均相对误差为3.97%，最大误差为16.02%，标准差为4.97%。由于最外圈网格几何中心所在半径为31.5 cm，因此，当源所在半径大于31.5 cm 时，活度重建值偏大，且随着源半径增加迅速增加，与图17（a）的结果符合。分别计算10组多点源活度重建结果的相对误差，其平均值为28.61%，最大值为80.63%，标准差为56.38%。

图17 TGS活度重建结果 (a) 单点源，(b) 多点源Fig.17 Activity reconstruction results of TGS (a) Single source, (b) Multi-sources

根据STGS 进行测量时，环源的活度重建结果如图18所示。当网格数目为3时，50组单环源活度重建值与真实值的相对误差的平均值为44.53%，最大值为689.46%，标准差为141.67%。10组多环源活度重建结果的相对误差的平均值为46.07%，最大值为133.28%，标准差为71.54%。当网格数目为5 时，50 组单环源活度重建结果的相对误差平均值为22.73%，最大值为251.83%，标准差为48.44%。10组多环源活度重建结果的相对误差的平均值为8.95%，最大值为23.14%，标准差为31.53%。

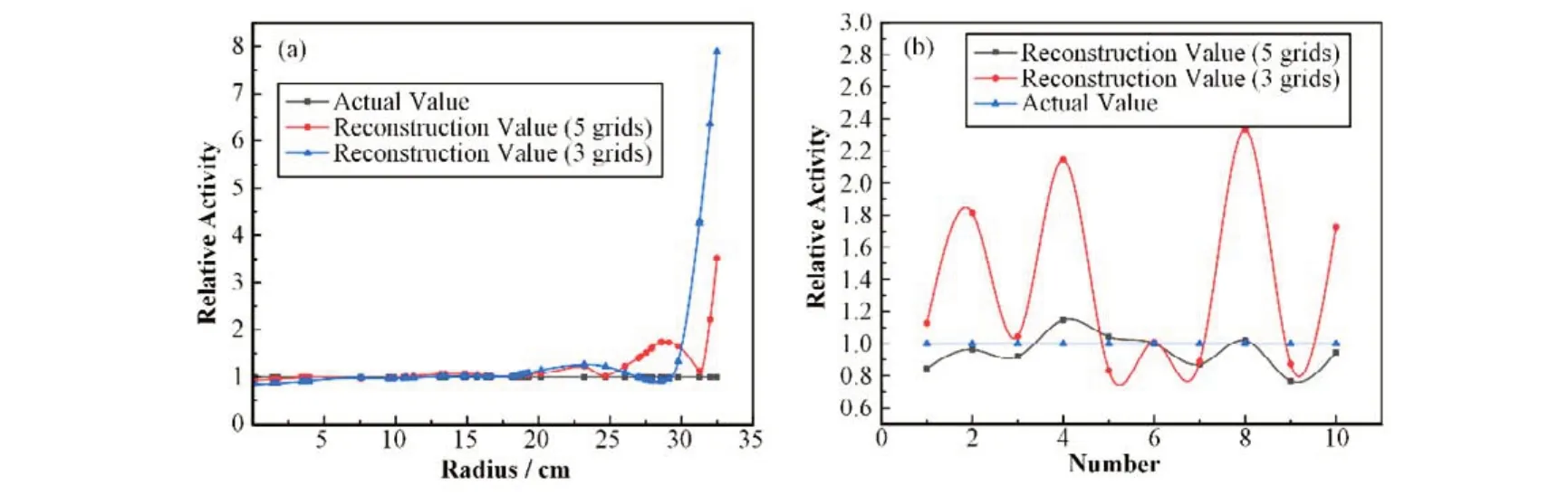
图18 STGS活度重建结果 (a) 单环源，(b) 多环源Fig.18 Activity reconstruction results of STGS (a) Single source, (b) Multi-sources

从图18（a）可知，当环源半径小于20 cm时，用3网格和5 网格划分方式进行活度重建的误差均较小，当环源半径大于20 cm 时，随着环源半径增加，环源先远离某一网格的中心再靠近下一网格的中心，活度重建误差先增加再减小。由于3 网格划分时最外圈网格的几何中心半径为29.5 cm，5 网格划分时最外圈网格的几何中心半径为31.5 cm，因此，当环源半径大于最外圈网格的几何中心的半径之后，活度重建值偏大，误差随着源半径增加快速增加。对于靠近废物桶边缘的环源，增加网格数量可以有效提高活度重建的精度；对于废物桶内部的环源，3网格和5网格划分方式对活度重建的精度的影响不大。当废物桶内有多个环源时，根据3 网格划分的活度重建的误差明显高于5网格的误差，因此，对于多环源情况，增加网格数量可以提高测量精度。但是测量次数和总时间也会随之增加。

3.4 结果对比与分析

不同测量方法下的活度重建误差如表6、7 所示。其中，NGS 表示新方法，TGS-n或者STGS-n表示根据n个网格进行TGS或者STGS（n=3，5，60）。

表6 多源活度重建结果Table 6 Activity reconstruction results of multi-source

假设探测器在每个测量位置上的测量时间为无量纲单位1，则SGS 的测量时间为1，3 网格的STGS为3，5 网格的STGS 为5，60 网格的TGS 为60，新方法的为3。

可以看到，对于单环源，新方法进行测量的精度达到了基于60 网格划分的TGS 的精度。相比于SGS，新方法精度提高了一个数量级。相比于STGS，新方法进行活度重建时的误差基本不受环源半径的影响，可以完成对废物桶边缘的环源活度的准确重建。当废物桶内存在多个源时，新方法的平均相对误差仅为SGS 与STGS（3 网格）的误差的一半，与60 网格划分的TGS 的误差接近；同样，除了STGS（5 网格），新方法的误差最大值仅为其他方法的1/2或者1/3。此外，新方法的测量位置较少，其总测量时间为基于60 网格划分的TGS 方法的1/20。新方法在保证了高测量精度的前提下，大大缩短了测量时间。

4 结语

针对传统无损测量方法SGS 精度低、TGS 测量时间长的问题，本文提出了基于神经网络的废物桶活度测量方法。该方法通过不同测量位置的探测器计数率可以快速精准地输出废物桶的等效环源的半径，从而实现准确的活度重建。分别进行了50组单Co-60 源和10 组多Co-60 源的模拟测量和活度重建，得到了以下结论：

1）新方法可以快速、准确地得到等效环源的半径。对于50 个随机生成的Co-60 环源半径，环源半径的预测值与真实值平均绝对误差为0.429 cm，均方根误差为0.536 cm。

2）利用新方法对400 L 水泥废物桶进行模拟测量与活度重建时，对于50组单Co-60源，活度重建值与真实值的平均相对误差为4.26%，且对废物桶中心和边缘区域的源的活度重建误差小于10%。而SGS的平均相对误差为68.15%，且对废物桶中心和边缘区域的源的活度重建误差达到100%。基于60网格的TGS 平均相对误差为3.97%。对于10 组多Co-60 源，新方法平均相对误差为24.27%，SGS 为48.02%，60网格的TGS为28.61%。说明新方法的测量精度远高于SGS，达到了TGS 的水平，但是其测量时间仅为相同精度TGS的1/20。

3）利用STGS 对其进行单Co-60 源的模拟测量与活度重建时，活度重建值受源半径影响较大，而新方法基本不受源半径的影响。对于多Co-60 源，在相同测量时间下，新方法的平均相对误差均为STGS的一半。

4）本文使用的神经网络训练集目前只包括400 L 水泥废物桶，待测核素为Co-60，因此目前神经网络只能对400 L 水泥废物桶中的Co-60 进行预测，若要对其他类型废物桶、其他密度介质、其他核素进行预测，需要在训练集中添加对应工况的结果以及增加神经网络输入层神经元的数量。

综上所述，对于介质均匀分布的废物桶，本文提出的新方法相较于传统测量方法，在保证了高测量精度的前提下大大缩短了测量时间，为低中放固废的快速测量提供了技术支撑。

作者贡献声明舒旻翔负责直接参与论文研究、模拟计算以及论文撰写；单陈瑜负责提供技术支持；顾卫国负责提供论文指导与技术支持；王德忠负责提供技术支持。