基于KZ 滤波法的江淮地区PM2.5 浓度变化影响分析
董 昊,王 欢,吴明胤,张付海
安徽省生态环境监测中心,安徽 合肥 230071
20 世纪初,随着我国经济的高速发展,环境空气污染形势较为严峻,以雾霾天为代表的污染天在京津冀、长三角以及汾渭平原等区域时有发生。 细颗粒物PM2.5作为雾霾天的主要影响因子一方面会降低能见度,影响交通安全,另一方面则会通过呼吸道进入人体肺部,危害人体健康[1]。《中共中央关于制定国民经济和社会发展第十四个五年规划和二○三五年远景目标的建议》要求基本消除重污染天气,因而为进一步治理PM2.5,对已采取的管控措施效果进行评估显得尤为重要。
国内外学者研究表明,污染源排放与PM2.5浓度的变化息息相关,是造 成PM2.5污染的根本原因,但气象条件对大气环境中PM2.5物理传输和化学转化也有着重要影响,其中风速、风向、温度、相对湿度以及混合层厚度等气象因素对PM2.5浓度有着显著影响[2-3]。 因而要量化管控措施效果,对气象因素的扣除尤为重要。 目前,对环境空气短期治理中管控效果评估主要采用数值模型进行定量分析,许艳玲等[4]采用WRF-CMAQ模型系统定量分析了2016 年气象和排放因素变化导致全国PM2.5年均浓度下降幅度分别为4%和3%,王文丁等[5]使用基于嵌套网格空气质量预报模式(NAQPMS)分析区域联防联控应急减排对成渝地区PM2.5浓度降低率为5%~11%。 但受限于空气质量数值模式的性能、排放清单的不准确、化学动力学机理的复杂以及其他的不稳定因素,不同模式间的评估结果存在一定的差异性,对污染物浓度长时间序列变化趋势分析存在局限性[6]。 因此,对长期污染物浓度变化趋势分析采用Kolmogorov-Zurbenko(KZ)滤波法被更广泛使用,其原理是利用污染物浓度变化的频域特性对其时间序列进行不同时间尺度分离,并通过逐步回归的方法得到气象条件对污染物浓度变化的影响。
安徽省位于长江三角洲地区,有八百里的沿江城市群和皖江经济带,尤其是江淮之间及沿江区域近年来经济高速发展,城市化、工业化程度进展较快。 本文以沿江地区的合肥、芜湖和马鞍山3 个城市为研究对象,分析2018—2020 年各城市PM2.5和气象参数日数据,从而量化“十三五”期间气象条件对沿江地区的PM2.5浓度长期变化的影响,以期有助于探讨经济高速发展下城市减排措施的实施效果。
1 研究方法
1.1 观测数据
本研究选取2018 年1 月1 日—2020 年12 月31 日合肥、芜湖和马鞍山3 个城市共计10 个国控站点的监测数据(具体监测站点信息见表1),根据《环境空气质量评价技术规范(试行)》(HJ 663—2013)[7]和《环境空气质量标准》 (GB 3095—2012)[8]评价各城市PM2.5日均浓度,进行KZ 滤波统计分析。 同时,为保证PM2.5监测数据与气象数据相匹配,选取同站点监测的气象参数,包括日平均气压(P)、日平均气温(T)、日平均相对湿度(RH) 和日平均风速(v),并进行数据整理。
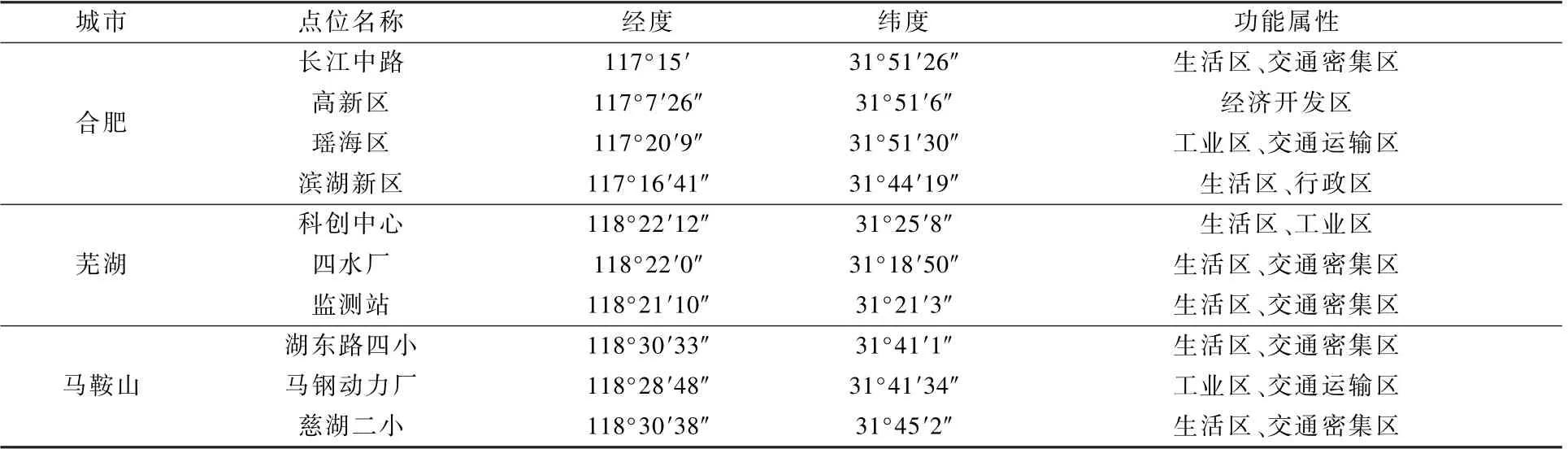
表1 空气质量监测站点信息及分布Table 1 Information and distribution of air quality monitoring stations
1.2 研究方法
滤波统计是一种时间序列分析方法,其原理是利用原始参数变化的频域特性对其时间序列进行不同时间尺度的分离。 对某一原始参数的时间序列A(t),其模型可表示为
式中:W(t)是参数短期分量;S(t)是参数季节分量;e(t)是参数长期分量。 其中,针对大气环境中PM2.5浓度的时间序列变化,其短期分量主要受短时天气系统影响,而排放源除了在特定节假日或其他特殊事件会显著影响浓度变化外,其余时段变化总体较小。 季节分量则是地球公转导致太阳角度的变化,使得气象条件的影响出现季节性变化,例如降水、季风以及气温的变化,同时因季节变化导致的污染排放也是影响之一。 长期分量变化的影响因素较多,主要包括区域内气候变化趋势、污染物的排放总量、经济发展状况以及当地相关政策[9]。
KZ 滤波是一种低通滤波,是m 个点的滑动平均滤波器的p 次迭代。 其计算公式:
式中:Yi为经KZ 滤波后的时间序列;m 为滑动窗口长度(m=2k+1);i 为序列的时间间隔;j 为滑动窗口变量;k 为Ai在滤波时其两端的滑动窗口长度。 将滤波后的时间序列作为下一次滤波的原始时间序列进行计算,根据计算需求,重复执行p次,得到最终的滤波结果用KZ(m,p)表示。 不同尺度的滤波是通过调整参数m 和p 来控制的,其中参数m 和p 与有效滤波宽度N 满足如下公式[10]:
根据RAO 等[11]和吴宜航等[12]的研究结果,选取KZ(365,3)和KZ(15,5)进行滤波处理,有效滤波分别为33 d 和632 d。 其中,通过KZ(365,3)滤波可以提取时间序列的长期分量,而经过KZ(15,5)滤波后的时间序列可定义为基线分量XB(t),代表季节分量和长期分量的总和,具体公式:
根据式(1)、式(4)和式(5)可以得到季节分量和短期分量的计算公式:
为进一步消除气象因素对PM2.5浓度的影响,本研究通过以气象参数为自变量的多元线性回归,分别就短期分量和基线分量构建气象要素与PM2.5的关系模型,并计算各分量回归模型的解释方差:
式中:VE 代表解释方差;varA(t)表示污染物原始序列方差;varε(t)表示残差序列方差。 解释方差越大,气象要素对原始序列的影响越大,解释能力越强。
各分量与回归模型预测值的残差序列即为剔除了气象参数影响的PM2.5浓度序列,即由污染排放导致的PM2.5浓度变化。 其中,原始序列的总残差序列ε(t)是短期分量回归残差εM(t) 与基线分量回归残差εB(t) 之和,计算公式:
继续对总残差序列做KZ(365,3)滤波处理,消除其他未参与拟合的气象因子的影响,获得受排放变化影响的PM2.5浓度长期变化分量εL(t) 。将变化分量与原始序列的长期分量均值相叠加,得到仅由污染源排放影响的PM2.5浓度长期分量时间序列eadj(t):
基于排放源和气象条件对PM2.5浓度影响的区分,计算2018—2020 年合肥、芜湖和马鞍山扣除气象条件后PM2.5浓度,对比分析浓度变化,从而评估分析时段气象条件和污染源减排措施对PM2.5浓度趋势变化的贡献。
2 结果与讨论
2.1 KZ 滤波后PM 2.5 的时间序列特征
根据《环境空气质量标准》(GB 3095—2012)和《环境空气质量指数(AQI)技术规定(试行)》(HJ 633—2012)中的规定,PM2.5的日均二级质量浓度限值为 75 μg/m3, 日均浓度超过150 μg/m3即为重污染。 图1 为PM2.5日浓度原始序列,由图1 可知:合肥、芜湖和马鞍山PM2.5的日变化趋势较为一致,日超标天主要集中在冬季,其中PM2.5日均浓度超过150 μg/m3的重污染天占总天数的比例分别为0.6%、1.1% 和0.7%。 统计分析2018—2020 年3 个城市的重污染天数变化情况,发现3 个城市重污染天数均呈现逐年减少趋势;对比城市间日均变化,合肥和芜湖PM2.5的日超标天数相对较多,超标率分别为10.3%和10.6%,马鞍山PM2.5污染程度相对较轻,日超标率为8.6%。
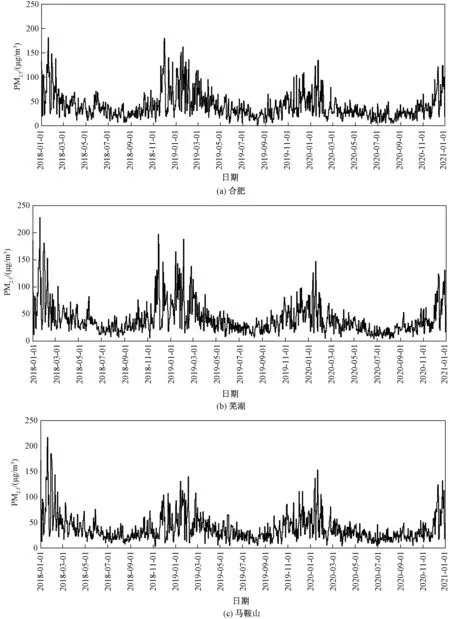
图1 合肥、芜湖和马鞍山PM 2.5 的原始时间序列A(t)Fig.1 The original time series A(t) of PM 2.5 in Hefei,Wuhu and Ma'anshan City
图2 ~图4 为合肥、芜湖和马鞍山3 个城市代表站点的PM2.5日浓度经KZ 滤波法处理后得到的时间序列。 短期分量变化如图2 所示,合肥、芜湖和马鞍山的高频变化较为一致,振幅范围分别为-65 ~+101、-76 ~+135 和-76 ~+122,反映了周期小于33 d 的PM2.5浓度波动情况,考虑污染排放量在短期内总体较为稳定,因而短期分量的波动主要是受本地天气变化影响。 同时,3 个城市在冬春季(11 月至次年3 月)波动明显强于其余时段,说明不同季节的天气影响存在差异,冬春季受本地天气变化影响更为显著。 因而在冬春季进行人影等气象作业,能更易达到本地PM2.5浓度削减的目的。
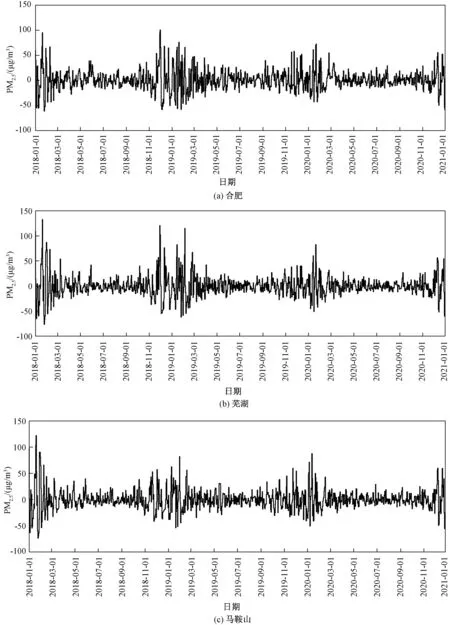
图2 合肥、芜湖和马鞍山PM 2.5 经KZ 滤波分解后的短期分量序列W(t)Fig.2 The short-term component W(t) of PM 2.5 by the KZ filter in Hefei,Wuhu and Ma'anshan City
去除短期分量的影响后,季节分量(图3)反映的是周期为33—632 d 的PM2.5浓度波动,主要是受本地排放源生产周期和气象季节条件变化影响,合肥、芜湖和马鞍山的季节分量变化波动基本一致,呈现明显周期季节特征。 其中,各城市浓度峰值主要集中在12 月至次年1 月,主要原因一方面是气温偏低,大气混合层较低,相对湿度较高,天气系统以静稳为主,大气水平和垂直扩散能力差,有利于本地污染物的累积[13],另一方面江淮之间的冬季主导风向为偏北风,京津冀及周边地区冬季采暖导致的区域性污染输送影响较为显著[14]。 但在春季PM2.5浓度也会出现短时的上升,如2018 年5 月下旬,这是由于上游沙源地起沙后对江淮之间区域的输送影响[15],其中受地理位置的影响,合肥受沙尘影响更为明显,PM2.5浓度的波动较芜湖和马鞍山更为显著。 而在7—8月,受梅雨季影响叠加夏季有利的气象条件,3 市降水多、温度较高,大气垂直对流较为活跃,有利于污染物的扩散和沉降,故均在此时段出现PM2.5浓度波谷。 此外,不同城市间的波动周期也存在一定的差异性,如合肥和芜湖在2018 年11 月至2019 年1 月的峰值出现分叉,而马鞍山未出现;波谷出现先后顺序为马鞍山>芜湖>合肥。
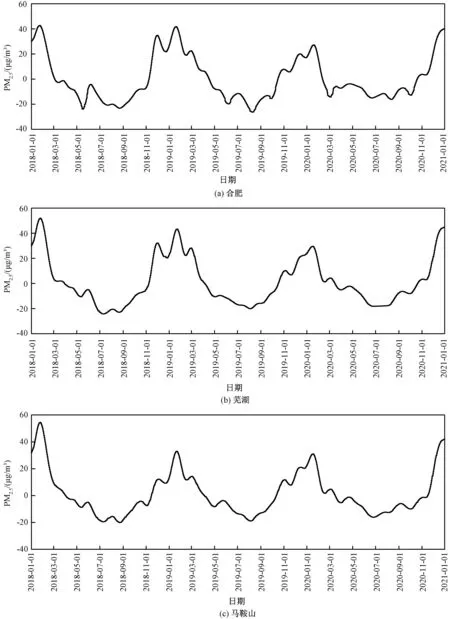
图3 合肥、芜湖和马鞍山PM 2.5 经KZ滤波分解后的季节分量序列S(t)Fig.3 The seasonal component S(t) of PM 2.5 by the KZ filter in Hefei,Wuhu and Ma'anshan City
图4 为滤波后的长期分量序列e(t),其滤波周期是632 d,其浓度波动反映的是区域污染物排放总量和气候变化等因素影响结果。 各城市的变化趋势总体较为一致,呈现下降趋势,其中合肥和芜湖在2018 年11 月至2019 年3 月出现轻微波动,随后下降趋势趋于明显,而这种变化趋势是无法直接从原始序列中解读的,进一步说明采用时间序列模型进行分析的必要性[16]。 合肥、芜湖和马鞍山长期分量下降速率分别为3.6、3.8 和2.6 μg/(m3·a),PM2.5年均值下降速率为3.3、4.3 和2.3 μg/(m3·a),对比二者发现,气象因素对合肥和芜湖PM2.5浓度下降呈现抑制作用,而对马鞍山则是促进作用。 此外,2018—2019 年合肥和芜湖PM2.5的长期分量明显高于马鞍山,这一方面是合肥和芜湖的本地污染源排放更为严重,包括工业企业废气、机动车尾气以及建筑工地扬尘等[17];另一方面江淮之间区域在气候上总体会受到北方PM2.5污染传输影响,相对于马鞍山,合肥和芜湖的地理位置更为偏北,受PM2.5污染传输影响更为显著。 但随着合肥和芜湖的工业结构的转型,电厂等燃煤企业的超低排放,各市间的污染排放量逐渐接近,PM2.5的浓度水平在2020 年已经与马鞍山基本趋于一致。
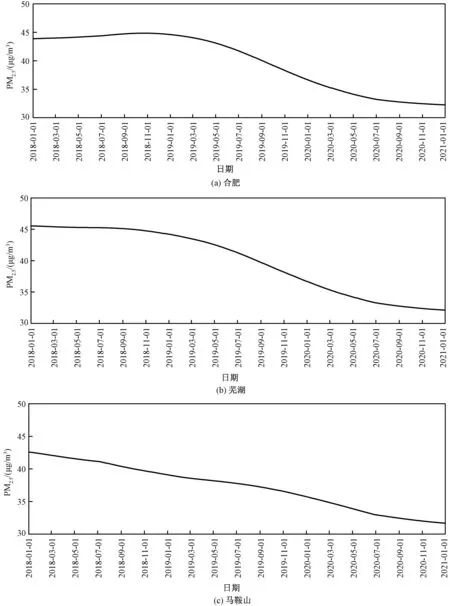
图4 合肥、芜湖和马鞍山PM 2.5 经KZ滤波分解后的长期分量序列e(t)Fig.4 The long trend com ponent e(t) of PM 2.5 by the KZ filter in Hefei,Wuhu and Ma'anshan City
为进一步验证KZ 滤波的准确性,选取各分量的协方差之对原始序列方差的贡献来检验时间序列分解效果,贡献越小,说明KZ 滤波分解效果越好,各分量越独立。 由表2 可知,3 个城市的原始序列经KZ 滤波后,协方差对总方差的贡献均低于10%,说明各城市分解后的分量之间相对较为独立,相互间的干扰较小。 而分析各分量方差对总方差的贡献情况,可以发现各市中短期分量的贡献最大,均超过50%,其次是季节分量,贡献率范围为40.4%~41.6%,而长期分量贡献占比最少,其中,马鞍山的贡献率仅为0.9%,这说明PM2.5浓度的变化主要受污染源排放和气象条件的短期和季节性变化影响,这与秦人洁等对石家庄、保定和张家口PM2.5的分析结果较为一致[18]。

表2 合肥、芜湖和马鞍山PM 2.5 各分量方差对总方差的贡献率Table 2 Contribution of each component to the total variance of PM 2.5 in Hefei,Wuhu and Ma'anshan City
2.2 气象因素对PM 2.5 不同分量的影响
多项研究表明,PM2.5的浓度变化受气象因素影响较为显著,为进一步探究经KZ 滤波后不同分量下PM2.5与各气象因子的相关性,本研究使用Spearman 相关系数法进行分析,结果见表3。相对于长期分量中,PM2.5与气压呈现弱负相关,在季节分量中则为显著正相关,这与王嫣然等在北京地区对不同季节PM2.5与气象因素的分析结果一致[19];与气温的相关系数在季节和长期分量中呈现负值,而在短期分量中为正值,这主要是气温上升会促进大气垂直运动,有利于PM2.5的垂直扩散和稀释,但若在短期内有逆温层存在,随着气温的升高,有利于大气稳定,大气混合层高度偏低,从而使得近地面污染物聚集[20];相对湿度和风速与PM2.5有着显著相关性[21],其中相对湿度在长期分量中与PM2.5呈现负相关,但在合肥的短期和季节分量出现正相关,这有可能是相对湿度较高导致PM2.5吸湿增长;风速对PM2.5的影响主要是通过水平扩散,随着风速增大,PM2.5的传输速率增加,污染物浓度下降,因而风速在短期和季节分量上与PM2.5呈现负相关,但城市的基础设施建设作为颗粒物的重要排放源,在风速增大的时候,会造成建筑工地扬尘扩散,使得空气中颗粒物浓度上升,这可能是风速与PM2.5长期分量呈现正相关的原因[20]。 综上,各气象因子在不同时间尺度下对PM2.5的影响作用偏差较大,应综合考虑不同时间尺度下气象条件对污染物的影响。

表3 合肥、芜湖和马鞍山PM 2.5 与气象因子的Spearm an 相关系数Table 3 Spearm an's correlation coefficients between PM 2.5 and meteorological factors in Hefei,Wuhu and Ma'anshan City
2.3 基于气象因素调整PM 2.5 的浓度变化
为进一步消除气象因素对PM2.5浓度变化的影响,根据上述气象因子对经KZ 滤波后PM2.5时间序列进行多元线性回归分析,并构建统计模型。由表4 可知,各城市均呈现出长期分量的解释方差最高、季节分量次之、短期分量最低的变化趋势。其中,各城市的长期分量和季节分量解释方差为87.9%~99.2%,可以认为长期分量和季节分量基本能通过选取的4 个气象因子变量来解释[20]。
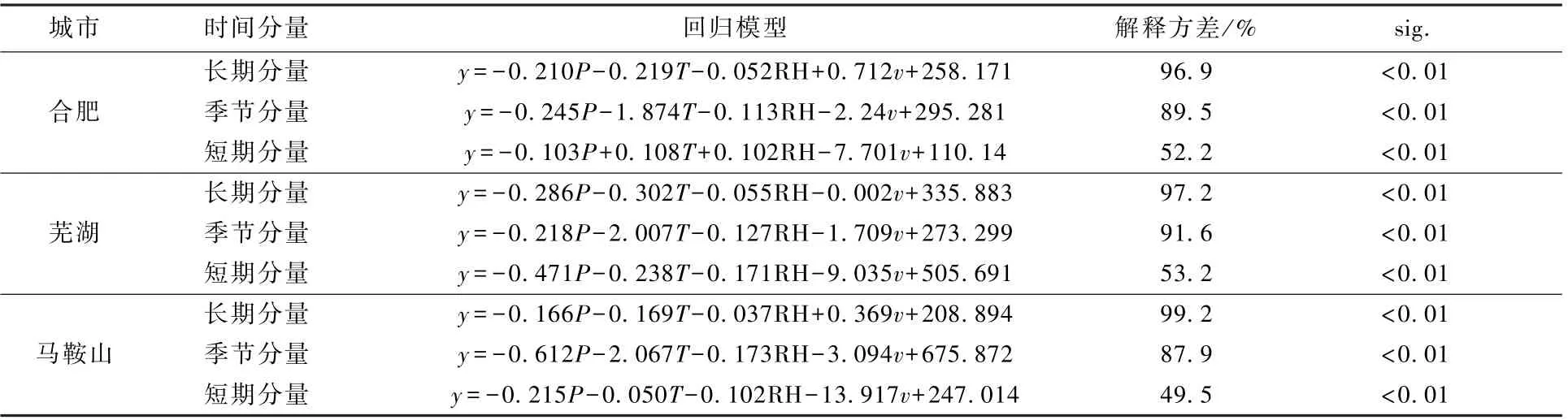
表4 合肥、芜湖和马鞍山PM 2.5 短期分量、季节分量和长期分量的回归模型分析Table 4 Regression model of PM 2.5 concerning the short-term component,seasonal component,and long-trend component by the stepw ise regression in Hefei,Wuhu and Ma'anshan City
图5 是依据回归模型和残差分析后绘制的PM2.5浓度长期分量变化趋势图。 由图5 可见:各城市消除气象因素影响后长期分量总体有所下降,尤其是2018—2019 年,说明气象条件整体不利于PM2.5的改善,这与梅梅等在京津冀采用城市大气污染数值预报系统进行分析得到2019 年气象条件对PM2.5浓度上升贡献9.96%的结果较为一致[22];而在2020 年下半年,气象条件则对PM2.5的影响呈现改善作用。
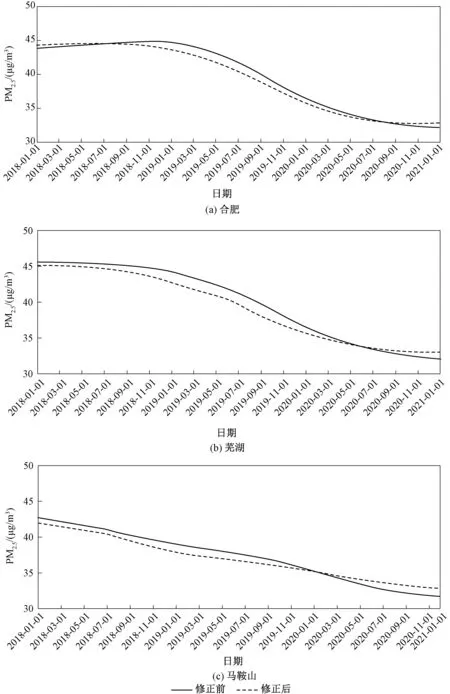
图5 合肥、芜湖和马鞍山经气象修正前后PM 2.5 浓度长期分量变化趋势Fig.5 Variations of long-trend component of PM 2.5 concentration before and after meteorological adjustm ent in Hefei,Wuhu and Ma'anshan City
对比各城市2018 年和2020 年长期分量修正前后的PM2.5浓度均值,其中2018 年与2020 年长期分量修正前PM2.5浓度均值的差值即为污染源与气象条件的总贡献,而长期分量修正后的差值为污染源的总贡献,具体结果见表5。 同2018年相比,2020 年合肥、芜湖和马鞍山PM2.5污染均显著改善,污染源减排措施仍是PM2.5污染改善的主要因素,其中气象条件对合肥、芜湖和马鞍山PM2.5改善的贡献率分别为 1.0%、 7.2% 和17.3%。

表5 合肥、芜湖和马鞍山减排措施和气象条件对PM 2.5 浓度改善的贡献情况Table 5 Contribution of emission reduction measures and meteorological conditions to the improvement of PM 2.5 in Hefei,Wuhu and Ma'anshan City
本研究基于KZ 滤波法评估了气象和污染源对3 个城市PM2.5的影响情况,但仍有其不确定性。 主要包括:①监测站点对城市的代表性有限,不同区域的PM2.5监测数据和气象条件都存在差异,尤其是近地面气象参数,受各种条件的制约,本研究仅选取10 个站点数据进行了均值处理;②基于多元线性模型进行拟合时,采用的拟合因子不够全面,拟合方程仅考虑气象因子与PM2.5浓度之间的关系,未考虑大气环境中二次生成对PM2.5的贡献。 ③贡献分析采用的是长期分量的计算结果,对于短期和季节分量中气象条件影响未进行剥离。
2.4 基于数值模式的情景分析
嵌套网格空气质量模式系统(NAQPMS)模式采用中尺度天气预报模式(WRF)输出的气象要素场作为的动力驱动,美国国家环境预报中心的NCEP 再分析数据为初始条件和边界条件,基于清华大学MEIC 清单为污染排放源清单,设置模拟区域为三重区域嵌套,网格分辨率分别为27、9、3 km,第三层网格覆盖安徽省全境。 本研究采用NAQPMS 模型进行3 个城市的情景模拟,保持排放源清单不变,第1 组模拟方案采用2018 年的气象场,第2 组模拟方案采用2020 年的气象场,两者模拟PM2.5浓度值为气象条件带来的浓度变化。
采用标准化分数偏差(MFB)对NAQPMS 模型模拟结果进行评估[式(11)]。
式中:Cm为模型模拟值;Co为实际监测值。
数字模型模拟结果显示,2018 年合肥、芜湖和马鞍山的PM2.5模拟值与实测值的平均偏差分别为11.9,13.6 和7.8,MFB 分别为23.1%,14.9%和28.2%,模拟结果在理想范围内[23],而造成模拟值偏高的原因可能是源清单的不确定性和模型本身化学机理的不完善。
为缩小模式模拟的差异,根据2018 年数据对3 个城市采用最小二乘法,构建PM2.5浓度模拟值与实测值的线性拟合关系(图6)。 基于拟合方程对2020 年3 个城市模拟值进行调整,调整后的PM2.5浓度为排放强度与2018 年一致污染物能达到的浓度水平。
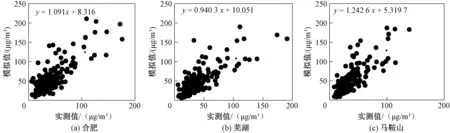
图6 2018 年合肥、芜湖和马鞍山PM 2.5 浓度模拟值和实测值线性拟合Fig.6 Linear regression of simulated and observed PM 2.5 concentrations in Hefei,Wuhu and Ma'anshan City in 2018
图7 为NAQPMS 模式模拟的气象和污染源变化对2020 年3 个城市PM2.5浓度的影响。 结果显示,相比于2018 年,2020 年合肥和马鞍山PM2.5浓度下降的主要贡献来自于减排措施,与KZ 滤波的结论较为一致;芜湖PM2.5浓度下降贡献中,减排措施和气象条件分别占比42.5%和57.5%,较KZ 滤波统计算法结果有所偏差,其原因可能是实际减排控制措施的执行效果好于减排预期效果,致使数值模型对减排措施存在低估。
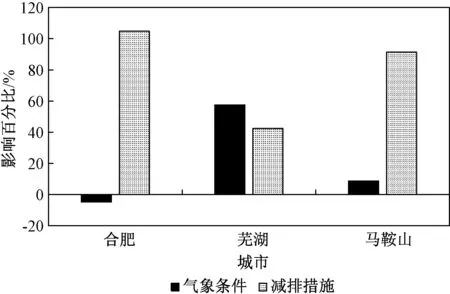
图7 基于NAQPMS 模式合肥、芜湖和马鞍山减排措施和气象条件对PM 2.5 浓度改善的贡献情况Fig.7 Contribution of emission reduction measures and meteorological conditions to the improvement of PM 2.5 in Hefei,W uhu and M a'anshan City based on NAQPM S
3 结论
1)江淮之间3 个城市PM2.5浓度各分量对原始序列总方差的贡献和均超过90%,KZ 滤波的分离尺度较为合理,能较为科学构建区域内PM2.5浓度时间序列模型,其中各分量中,短期分量对总方差的贡献最大,季节分量次之,长期分量贡献最少,说明PM2.5浓度时间序列的波动主要是受污染源和气象条件的短期和季节影响。
2)PM2.5浓度与气压、温度、相对湿度和风速均呈现一定相关性。 其中,在不同时间尺度下,气象因子对PM2.5的影响存在显著差异。
3)依据回归模型和残差分析后,修正气象条件对长期分量的影响,KZ 滤波统计结果显示2018—2020 年气象条件对江淮之间区域PM2.5污染改善影响存在波动,同2018 年相比,2020 年江淮之间PM2.5污染均显著改善,减排措施的贡献率为82.7%~99.0%;数值模式情景分析结果显示减排措施的贡献率为42.5% ~104.8%;因而,污染源减排措施是江淮之间PM2.5污染改善的主要因素。

