四元数在工业机器人编程操作中的应用

程福

（北京城市学院信息学部，北京 101300）

1 引言

相对于旋转矩阵、欧拉角、旋转向量等机器人姿态描述方法，四元数因其具有能够实现平滑插值、避免万向节死锁等优点，被广泛应用于机器人末端操作器（工具）的姿态规划中[1-2]。目前广泛应用的基于四元数的姿态插补算法主要有球面线性插值 (Spherical Linear Interpolation，SLERP) 和球面立体插值 (Spherical and Quadrangle，SQUAD)[3]。SLERP 算法计算简单，可以高效地实现两姿态间的平滑插值。

由于应用四元数能够确保工具在三维空间中姿态变换的平滑性，其在工业机器人研发中得到了深入的研究和广泛的应用，但介绍四元数应用于机器人编程操作的公开文献并不多见[4-5]。在机器人的编程操作时，可以应用四元数实现工具角位移的精确度和重复精度的准确检测，也可以进行直线运动轨迹的姿态规划。

2 四元数用作姿态描述和旋转变换

2.1 四元数与欧拉旋转定理

四元数是对复数的扩展。四元数实质上是实数、复数及三维空间向量的扩充，包含一个实部和三个虚部。一个复数表达式为a+bi。其中，a和b都是实数，i是单位虚数，i2=-1。一个四元数表达式：q=q1+q2i+q3j+q4k，其中i2=j2=k2=-1，ij=k=-ji，jk=i=-kj，ki=j=-ki，{q1，q2，q3，q4}都是实数，表示四元数的四个组成元素。

四元数的加法运算：如果p={p1，p2，p3，p4} 表示另一个四元数，则两个四元数加法运算：q+p=p+q=(q1+p1)+(q2+p2)i+(q3+p3)j+(q4+p4)k；四元数的乘法运算：qp=(q1p1–q2p2–q3p3–q4p4)+(q1p2+q2p1+q3p4–q4p3)i+(q1p3+q3p1–q2p4+q4p2)j+(q1p4+q4p1+q2p3–q3p2)k。

四元数的加法满足结合律和交换律。但是，四元数的乘法和矩阵的乘法相类似，只满足结合律，不满足交换律，即qp≠pq。

欧拉旋转定理指出，对于空间中任意姿态的坐标系，总可以在空间里找到某个轴，使其中一个坐标系绕轴旋转一个角度就能与另一个坐标系姿态重合。所以，坐标系在三维空间中的姿态可以用一个代表旋转轴的向量u和绕向量u旋转的角度θ来描述，向量u的方向遵循右手螺旋法则。如果用u与θ描述一个坐标系的姿态，那么-u与-θ，以及-u与 360°-θ分别描述的坐标系的姿态与该坐标系的姿态相同。

工具坐标系实现姿态变换的旋转轴如图1 所示，用向量及绕其旋转角度描述坐标系在三维空间的姿态如图2 所示。如果在关节空间围绕工具中心点（Tool Center Point，TCP）改变工具坐标系的姿态，即使绕世界坐标系的X，Y，Z轴进行多次旋转，仍然等效于工具坐标系绕经过工具中心点TCP 的一个向量u旋转角度θ实现姿态变换。如果工具中心点TCP 的位置不变，编程人员使用直线移动指令改变工具的姿态，大多数机器人的控制器会采用绕经过工具中心点TCP 的一个向量u旋转角度θ实现姿态变换，所应用的是基于四元数的SLERP 轨迹插值法[3]。

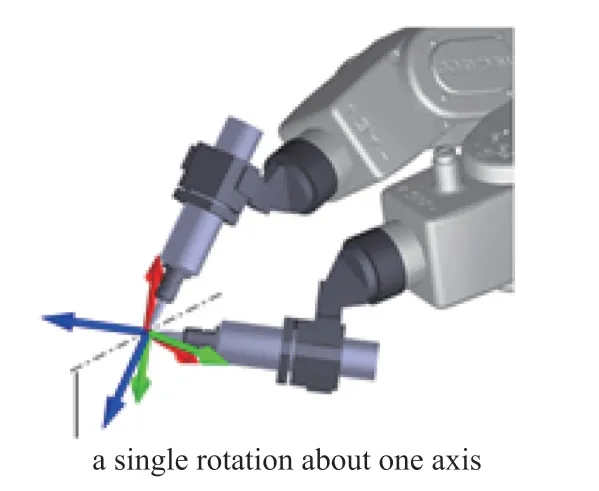
图1 工具坐标系实现姿态变换的旋转轴

图2 用向量及绕其旋转角度描述坐标系在三维空间的姿态

2.2 应用四元数描述三维空间的姿态

对于单位四元数q，|q|=q12+q22+q32+q42=1，q可以描述为q={cos(θ/2)，uxsin(θ/2)，uysin(θ/2)，uzsin(θ/2)}，其中，ux，uy，uz是向量u三个互相垂直的主轴的分量，θ是绕向量u旋转的角度。q所描述的姿态是由于世界坐标系姿态相同的四元数描述的坐标系绕以向量u为轴旋转角度θ变换而来。所以，仅用u和θ就可以描述坐标系在三维空间的姿态。

使向量u分别代表世界坐标系的z、y、x轴，则四元数描述的坐标系绕向量u旋转角度θ变换而来的姿态分别如图3a、3b 和3c 所示。

图3 四元数描述的坐标系绕世界坐标系z、y、x 轴旋转一定角度的姿态

由于同一个四元数描述的姿态与用绕向量-u旋转360°-θ角度的姿态相同，即q={cos(180°-θ/2)，-uxsin(180 °-θ/2)，-uysin(180 °-θ/2)，-uzsin(180 °-θ/2)}={-cos(θ/2)，-uxsin(θ/2)，-uysin(θ/2)，-uzsin(θ/2))=-q。所以，一个四元数与其四个组成元素取负值后的四元数，它们描述的是同一个姿态。

2.3 单位四元数用作旋转变换

如果Rq是3×3 旋转矩阵，其对应的姿态用四元数q来描述，Rp为另一个四元数p对应的3×3 旋转矩阵，那么旋转矩阵RqRp与四元数qp描述的姿态相同。由于两个3×3 旋转矩阵需要经过27 次乘法和10 次加/减法运算，而两个四元数相乘只需要经过16 次乘法和12 次加/减法运算，所以应用四元数描述姿态的优点是计算效率较高。

一个3×3 旋转矩阵的逆矩阵等于其转置矩阵，即Rq-1=RqT。四元数的求逆运算描述的姿态变换更为直观，它是由同一个坐标系绕向量u以-θ角度旋转而 来，即q-1={cos(-θ/2)，uxsin(-θ/2)，uysin(-θ/2)，uzsin(-θ/2)}={cos(θ/2)，-uxsin(θ/2)，-uysin(θ/2)，-uzsin(θ/2)}。因此，可以得到q-1q=qq-1={1，0，0，0}。这说明，四元数与其求逆后的四元数相乘得到的四元数描述的姿态与3×3 单位矩阵姿态相同。

如图4 所示，如果纯四元数v={0，vx，vy，vz}描述一个坐标系的姿态，单位四元数q作为坐标系姿态变换的算子，那么，四元数qvq-1描述的姿态与四元数v描述的姿态相同。

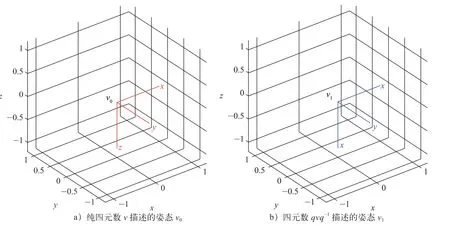
图4 四元数qvq-1 描述的姿态v1 与纯四元数v 描述的姿态v0 相同

应用四元数，可以实现与应用欧拉角法相同的工具坐标系的姿态变换；首先把应用欧拉角法实现姿态变换的三个分量角度分别转化为四元数，然后将这三个四元数相乘，依据四元数乘法的几何意义则得到表示旋转的四元数。

设欧拉角的三个旋转角度分量分别为，绕z轴旋转α角，绕y轴旋转β角，绕x轴旋转γ角。这三个旋转角度分量对应的四元数为qz，qy，qx，则Q表示最终得到的旋转四元数：

2.4 单位四元数与姿态变换矩阵的转换

对于单位四元数，其对应的姿态变换矩阵为。

3 应用四元数检测工具的角位移

等量的欧拉角变化并不一定对应等量的姿态旋转，对应同一个姿态，欧拉角的角度变化量可以有多组，而且姿态轻微的改变，欧拉角变换很大。所以，应用欧拉角很难准确评价实现姿态变换的角位移的精确度和重复精度；应用单位四元数能够很容易根据实现初始姿态变换到结束姿态的角位移，准确检测出角位移的精确度和重复精度。

如果q是描述工具坐标系在姿态1 时的四元数，p是描述工具坐标系在姿态2 时的四元数，则工具在姿态2相对于姿态1 时的姿态用四元数描述为

式中，wx，wy，wz是单位向量w的分量。公式（1）表明，工具从姿态q变换到姿态p，需要绕向量w旋转角度φ，如图5 所示。为了实现以最小角度的旋转，限定旋转角度范围为0<φ≤180，因此，如果d的第一个单元为负数，则计算角度φ时需要将d=—d，即cos(φ/2)，以确保总是取d的第一个单元数的正值来计算角度φ。由公式cos(φ/2)=可以求出旋转角度φ。

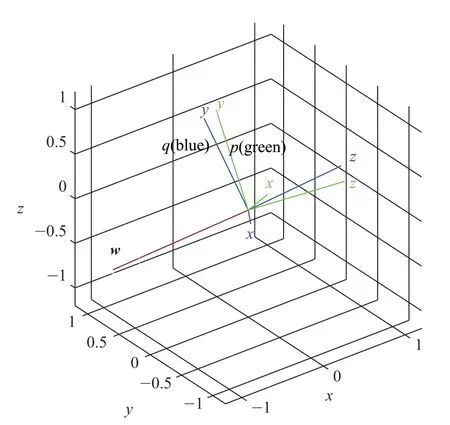
图5 四元数q 和p 描述的姿态在世界坐标系中的旋转变换

4 应用单位四元数实现机器人工具直线运动轨迹的姿态规划

尽管以逆时针和顺时针两个方向可以实现等效的姿态变换，但以小于180°的角度实现姿态变换是最快捷的角度变化路径，也是驱动转矩最小的角度变化路径。

为了实现四元数q描述的姿态以等角速度平滑变换到四元数p描述的姿态，需要应用公式（5）描述的球面线性插值SLERP 法得到相等的角度变化量的序列值。

式中，t∈[0,1],t=0 对应四元数q描述的姿态，t=1 对应四元数p描述的姿态。

根据前述分析，d=q-1p={cos(φ/2)，wxsin(φ/2)，wysin(-φ/2)，wzsin(-φ/2)}，球面线性插值法的公式可以视为实现四元数q描述的姿态以等角速度平滑变换到四元数p 描述的姿态，需要以角度φ旋转次。所以，dt={cos(tφ/2)，wzsin(tφ/2)，wysin(-tφ/2)，wzsin(-tφ/2)}。

如果令t=0，1/n，2/n，…，1，那么，球面线性插值法实质上是通过每次以相等的旋转角度φ/n，实现旋转角度为φ的姿态变换。应该注意，要确保φ小于180°。式（6）与式（5）等效，但更便于计算。式（5）中的每一个t值，对应一个四元数。

如果机器人的工具中心点TCP 位置不变，只是姿态发生变化，可以应用球面线性插值法以等角速度实现初始姿态平滑变换到结束姿态，如图6 所示。

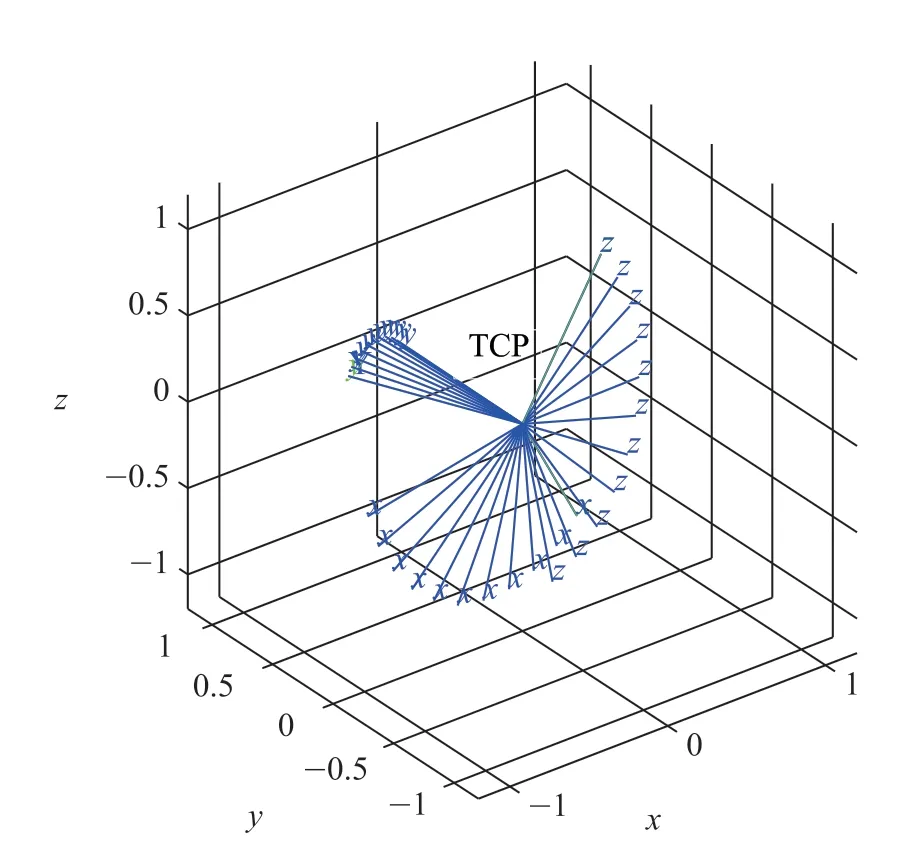
图6 机器人的工具中心点位置不变时姿态变换过程

根据程序6 的计算出来的序列姿态，应用工业机器人编程软件RoboDK 编程控制ABB 机器人实现工具的姿态变换过程如图7 所示[6]。

图7 机器人在工具中心点位置不变时姿态变换过程

如果机器人的工具中心点TCP 沿直线运动过程中不仅姿态发生变化，位置也发生变化。编程人员为了控制工具沿直线运动过程中的姿态和位置变换，可以应用球面线性插值（SLERP）法以等角速度实现工具从初始姿态平滑变换到结束姿态，应用式（7）描述的线性插值（LERP）法实现工具从初始位置经过若干序列点沿直线运动到结束位置，如图8 所示。

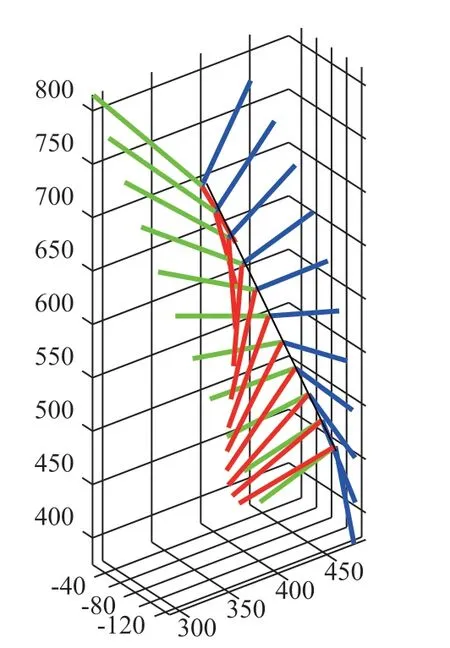
图8 应用SLERP 和LERP 在工具沿直线运动位姿平滑变换

根据程序7 的计算出来的序列位姿，应用工业机器人编程软件RoboDK 编程控制ABB 机器人实现沿直线运动时工具的姿态和位置变换过程如图9 所示。

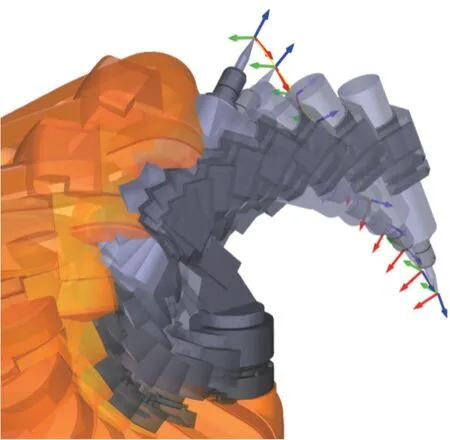
图9 机器人在工具沿直线运动位姿平滑变换

5 结束语

尽管绝大多数工业机器人软件采用欧拉角法描述机器人工具的姿态，但在机器人编程操作中应用欧拉角法能够准确地检测工具角位移的精确度和重复精度。编程操作人员应用四元数法不仅能够准确地检测工具角位移的精确度和重复精度，也可以根据操作任务要求（例如，要求以驱动转矩最小的角度变化路径进行姿态变换）重新进行机械臂工具的姿态规划。