二阶多元正规变化下投资组合损失的谱风险测度的渐近式
季海波
(宿迁学院 文理学院,江苏 宿迁223800)
0 引言
风险是金融体系与金融活动的基本属性之一,风险管理是各类金融机构所从事的全部业务和管理活动中最核心的内容.对于风险度量方法的研究最早可追溯到美国经济学家、金融学家Markowitz的著作《资产组合选择:投资的有效分散化》[1],其中的均值-方差模型为风险量化方法的开端.1990年代,国际清算银行引入一种针对市场风险的资本金要求,提出了风险价值(value-at-risk,VaR)的概念,对于损失随机变量X,其分布函数为F(x),则置信水平0<β<1下的风险价值定义为
VaR,β(X)=inf{y∈R|P(X≤y)≥β}=F←(β),
VaR,β(X)实际上是损失分布的β分位数.对于风险价值计算的相关研究可参见文献[2-5].风险价值在风险管理领域影响广泛,但自身具有局限性,它不符合一致性风险度量,且没有考虑尾部损失.1997年,Artzner等[6]提出了期望损失(expected shortfall,ES),定义为损失分布中超过置信水平β下的风险价值部分的损失期望值,表达式为
对ES的相关研究可参见文献[7-9].之后,Acerbi[10-11]引入更一般的一致性风险度量——谱风险测度(spectral risk measure,SRM),并指出ES是SRM的特例[10].谱风险测度的表达式为

(1)
其中,权重函数φ(p)为容许风险谱,具有下列性质:
1)非负性:φ(p)≥0;
3)弱增性:φ′(p)≥0.
Acerbi等[12]还对谱风险测度的计算及以该风险度量作为目标或约束条件的资产组合优化问题作了初步探讨;2020年,Xing等[13]研究了一阶多元正规变化尾下谱风险测度的渐近式,并利用随机模拟验证了谱风险测度的二阶展开式较一阶展开式更接近经验值.本文将文献[13]中的损失分布尾推广到二阶多元正规变化的情形,计算谱风险测度的渐近式.
1 基本概念
引入一维情形下的正规变化函数的定义.

(1)
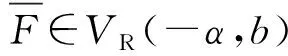
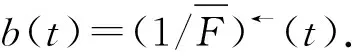
(2)
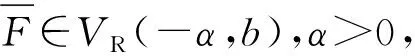
(3)
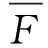
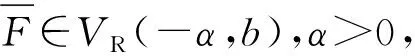
(4)
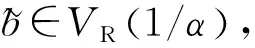
下面给出多维情形下正规变化函数的定义.
定义3[16]假设随机变量向量X=(X1,X2,…,Xd)取值于[0,∞)d中,如果存在函数b(t)→0(t→∞),b(t)∈VR(1/α),α>0,Radon测度ν≠0,使得当t→∞时,在M+(E)上有
其中:E=[0,∞]d{0},0为全0的d维向量,M+(E)为E的布雷尔子集上全体Radon测度组成的集合;上述收敛是指淡收敛,则称X是多元正规变化的,记作X∈VMR(-α,b,ν).
Radon测度ν(·)对相对紧集A⊆E有如下性质:
ν(kA)=k-αν(A),k>0.
定义4[17]假设X∈VMR(-α,b,ν),且存在一致符号函数A(t)→0,|A(t)|∈VR(ρ),ρ≤0,使得当t→∞时,有
(5)
其中:x∈(0,∞]d(∞,∞,…,∞);H是一个非零且有限的函数,则X为二阶多元正规变化的,且具有参数α>0,ρ≤0,记作X∈V2MR(-α,ρ,b,A,ν,H).
2 二阶多元正规变化下的谱风险测度的渐近式
给出两个在随机变量向量X上的假设,其分布函数为F.两个假设分别是在ν(·)相对于Lebesgue测度存在密度函数和不存在密度函数的情形下给出的.
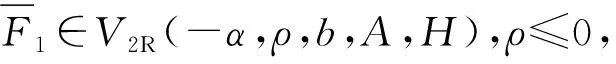
其中极限函数λ(·)≠0,且在={x∈E|‖x‖=1}上有界,满足λ(tx)=t-α-dλ(x),≠0在远离0的集合上可积,在上有限且有界.
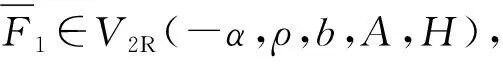

当X∈V2MR(-α,ρ,b,A,ν,H)时,在假设1和假设2下X都有相同的边缘分布,且都是二元正规变化的.对于投资组合损失
有如下引理.
引理2设X∈V2MR(-α,ρ,b,A,ν,H),α>1,ρ≤0,且ν({x∈R+d|xi>1})>0,ω∈Σd,则有
(6)
其中:Ωd={x∈R+d|ωTx>1},Γi={x∈R+d|xi>1},i=1,2,…,d.
证因为X∈V2MR(-α,ρ,b,A,ν,H),由定义4知,X∈VMR(-α,b,ν).由文献[2]中定理3.4.1的证明,有
从而可得
再由文献[8]中的结论,可知
故(6)式成立.

ωTX∈V2R(-α,ρ,b*,A*,H*),

证只需将文献[2]中定理4.2证明过程中的Γd换成Ωd,即可证.
推论1设X∈R+d,满足定理1的所有条件,则有
ωTX∈V2R(-α,ρ,b1,A1,H1),
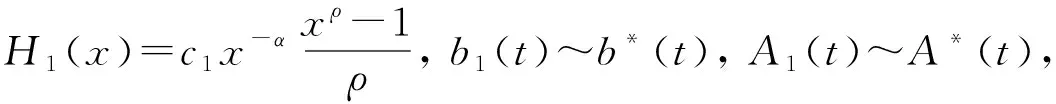
根据引理2,给出二阶多元正规变化下的谱风险测度Mφ1-β(ωTX)的渐近式,对应的风险谱函数定义为
(7)
其中φ1:[0,1]→R.
定理2设X∈R+d,满足定理1的所有条件,ν({x∈R+d|xi>1})>0,ω∈Σd,风险谱函数为(7)式,且对任意的1
(8)
则当β→1时,有
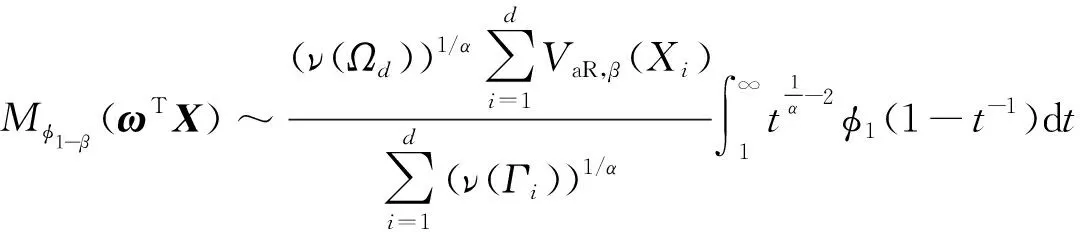
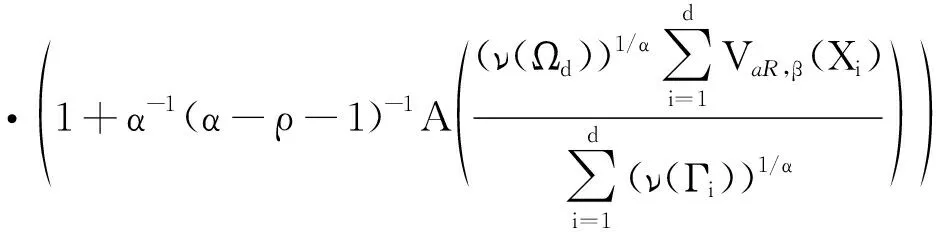
(9)
证由(1)、(7)式,有

令s=1-(1-β)t-1,换元可得

(10)
由推论1可知,X∈V2MR(-α,ρ,b,A,ν,H),从而可得
ωTX∈V2R(-α,ρ),α>1,ρ<0.
由定义2,有ωTX∈VR(-α).假设ωTX的分布函数为Fω,则
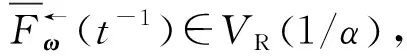
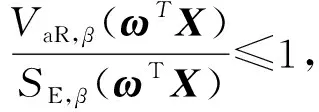

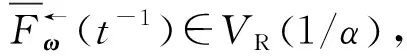
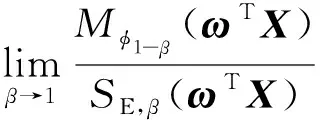
即当β→1时,
(11)
由文献[13]的引理3.3知,当β→1时,
(12)
结合(11)、(12)式,可得
(13)
再将(6)式代入(13)式,可得结论.
3 实例分析
例1假设X1,X2是独立同分布的随机变量,且共同的分布函数F满足
(14)
计算二维随机变量X=(X1,X2)对应的谱风险测度的渐进式.
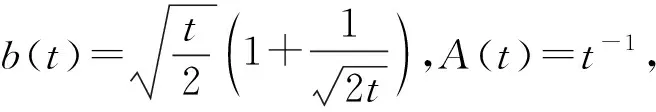
由定义2可知,X1∈V2R(-2,-1),其中α=2,ρ=-1.
记ν2(x,∞)=x-α,x>0,则有
故假设2成立.
再验证X=(X1,X2)∈VMR.对于x1>0,x2>0,有
且有
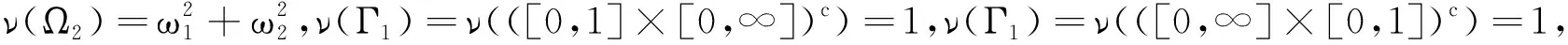
(15)
为了作比较,应用文献[13]中的定理3.2(8)式,得β→1时谱风险测度的一阶渐近式为
(16)
取幂风险谱函数
即可满足(8)式;再取ω=(0.5,0.5)T,利用Monte-Carlo模拟对二阶渐近式(15)与一阶渐近式(16)进行比较,具体步骤如下:
第1步假设X1,X2独立同分布于(14)式,随机产生105组X=(X1,X2)的样本,记作xi=(xi1,xi2)(i=1,2,…,105);
第2步产生投资组合损失ωTX=0.5(X1+X2)的样本;
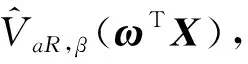
具体模拟结果见表1.
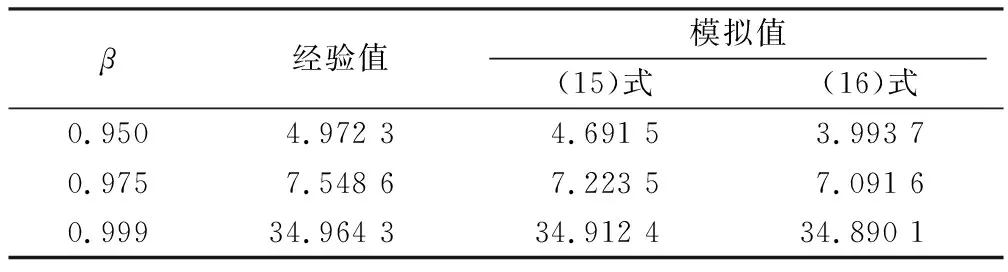
表1 不同β下谱风险测度渐近式与经验式的模拟值Tab.1 Simulated values of asymptotics and empirical formulas for spectral risk measures under different β
在实际应用中,风险谱函数的选择需要满足(8)式.由表1可知,无论β取何值,二阶多元正规变化下的谱风险测度较一阶情形都更加接近经验值;随着β的增加,(15)与(16)式的值都越来越接近经验值,且两者之间的绝对误差随着β的增大而减小.
对投资组合ωTX=αX1+(1-α)X2(0<α<1)在系数α取不同值时,进行同样的模拟,结果发现:只要α固定,则二阶多元正规变化下的谱风险测度较一阶情形下更接近经验值;且随着α的增加,两个渐近式的值越来越接近经验值.
可见,一旦投资项目数与组合系数固定,无论增加投资项目数量还是改变项目组合系数,变化规律都是一致的.

