Burgers方程的奇摄动初值问题的激波解
杜冬青, 刘树德
(1.江苏省徐州财经高等职业技术学校,江苏 徐州221008; 2.安徽信息工程学院,安徽 芜湖 241000)
0 引言
Burgers方程是模拟激波传播和反射的非线性偏微分方程,具体表达式为
它是Navier-Stokes方程中忽略压力项后的简化形式,被广泛应用于流体力学、非线性声学、气体动力学等工程科学领域[1-3].取Burgers方程中的ν为小参数(记作ε),考虑如下初值问题:
(1)
(2)
其中u1,u2为常数,且u1>u2.由于方程(1)中小参数ε与最高阶导数相乘,故(1)、(2)为奇摄动初值问题,初始条件的突变使得该问题的解在过渡层产生激波[4].
具有激波结构的解称为激波解.一些学者利用匹配渐近展开法[5-8]寻求激波解的渐近展开式,但这种方法需要进行内、外展开式匹配的讨论过程,且此过程相对比较复杂.为此,本文利用合成渐近展开法[9-15]构造问题(1)、(2)的激波解:首先,在激波位置两侧分别寻求具有边界层性质的近似式;再使用衔接法将对应的曲面光滑地衔接,构成激波解的形式近似;最后,运用渐近展开理论分析解的渐近性质,得到一致有效的渐近展开式.
1 构造形式近似式
为简单起见,只构造激波解的零次近似.根据激波结构性质,作变换
y=x-Ut,
(3)
代入问题(1)、(2),得
(4)
(5)
(4)式的退化方程为
(6)
变换(3)使得问题的解在y=0产生激波,任取y1<0和y2>0,在(6) 式两边对y从y1到y2积分,并利用边界条件(5),得
由此解出激波的传播速度
在变换(3)下,先将外展开式
代入问题(4)、(5),取零次近似,得
解得
(7)
其中每个vj(ξ,t)(j=0,1,2,…)满足
(8)
和
(9)
将
u=W(y,t,ε)+V(ξ,t,ε)
代入(4) 式,取零次近似,得
(10)
由于u1>u2,故沿y增大的方向激波传播速度减小,突变的条件使得校正项满足
v0(0+,t)=-v0(0-,t)=a,
(11)
其中
当y<0时,方程(10)转化为
(12)
(12)式两边从-∞到ξ积分,利用(8) 式,得
分离变量并两边积分,利用(11) 式,得
于是
(13)
类似地,当y>0时,方程(10)转化为
(14)
(14)式两边从ξ到+∞积分,利用(9) 式,得
再由(11) 式,得
于是
所得结果与(13) 式相同.由(7)、(11)式,可得
w0(0-,t)+v0(0-,t)=w0(0+,t)+v0(0+,t)
利用衔接法,定义
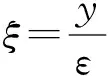
在-∞ (15) 利用Cole-Hopf变换,可求得问题(1)、(2)的精确解[1]为 其中 按照以上形式的构造,知 u(x,t)=u0(x,t)+O(ε),ε→0. (16) 下面分析(16)式的一致有效性.令 故当t→+∞时, 从而 类似地,令 故当t→+∞时, 从而 综上可得以下结论: h(x,t)→1,t→+∞. ii)若方程(1)中ε>0,且ε为小参数,则问题(1)、(2)为奇摄动初值问题.此时,对任意常数T>0,在u2T h(x,t)→1,ε→0. 进一步研究奇摄动初值问题,分x-Ut>0和x-Ut<0两种情况讨论. u0(x,t)=u2+EST,u(x,t)=u2+EST, 从而有 u(x,t)=u0(x,t)+EST,ε→0. u0(x,t)=u1+EST,u(x,t)=u1+EST. 从而有 u(x,t)=u0(x,t)+EST,ε→0. 可见,无论x-Ut>0还是x-Ut<0,总有 u2t 因此,得到如下结果. 定理1设u(x,t)是奇摄动初值问题(1)、(2)的解,则对任给的常数T>0,在u2T u(x,t)=u0(x,t)+O(ε),ε→0, 例1考虑奇摄动初值问题 (17) (18) 易得a=1,U=0,代入(15) 式,得 故对任给的常数T>0,问题(17)、(18)的解 在-T 例2考虑奇摄动初值问题 (19) (20) 令z=uet,则问题转化为 此为问题(1)、(2)的类型,且a=1,U=1.代入(15) 式,得 从而 故对任意常数T>0,问题(19)、(20)的解 在0 Burgers方程用于研究激波的一个原型问题,应用领域极其广泛.本文取Burgers方程中的常数为小参数,研究具有初值间断的奇摄动问题.奇异摄动方法包括匹配渐近展开法、合成展开法、多重尺度法等经典方法,在于寻求一致有效的渐近解,把非一致有效的展开式变为一致有效的展开式.需要指出的是,这里所说的一致有效性具有应用数学的特征,没有严格证明.由于本问题已经求出精确解,故运用渐近展开理论容易证明形式近似解的一致有效性,使得严密性分析得以简化.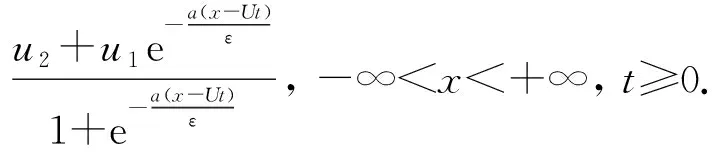
2 解的一致有效性
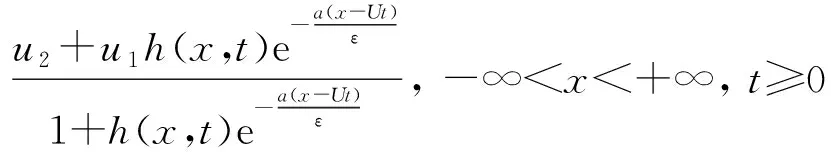
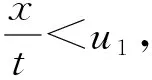
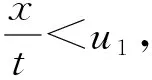
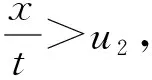
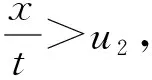
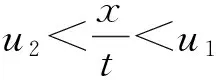
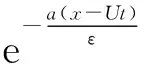
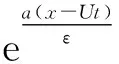
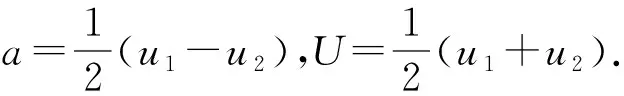
3 示例
4 结语

