大海则煤矿立井箕斗四角罐道水平力计算方法研究

黄博华，杨福珍，陈 哲，茹加宏，葛 辉

(1.中煤西安设计工程有限责任公司，陕西 西安 710054；2.西安建筑科技大学 土木工程学院，陕西 西安 710054)

煤矿立井提升容器在装卸载过程中，为了方便容器内煤炭、人员或货物的进出，同时确保容器稳定性，均需要由井筒内的端罐道固定转换为四角罐道固定。在装卸煤炭或进出货物、人员时，提升容器在四角罐道内会产生终端载荷的剧烈变化，使得提升容器发生水平平动和绕质心转动，并对四角罐道产生强烈的撞击，导致四角罐道受到水平作用力。另外，在上、下行启动时，提升容器缓慢加速离开井口或井底过程中会发生小幅度摆动，也会碰撞到四角罐道并产生水平作用力。上述两种工况下的撞击点、撞击次数、最大撞击力均难以确定，给四角罐道水平力研究带来困难。

目前，国内外仍缺乏提升容器对四角罐道作用水平力的研究。现行《煤矿立井井筒及硐室设计规范》[1]中，只给出了端罐道水平力计算公式。四角罐道因受力特征不明确、设计理论研究不足等影响，在结构设计中存在结构形式无法确定、结构安全性无法评估等问题，严重制约了四角罐道设计的安全性和经济性。

因此，进行煤矿立井提升容器对四角罐道的水平力特征研究，可为煤矿立井井口、井底金属支持结构受力分析[2-4]和煤矿立井四角罐道设计参数研究[5-9]提供依据。本文依据四角罐道水平力现场测试结果，找出四角罐道的水平力特征和变化规律，并通过回归分析建立提升容器作用于四角罐道的水平力与提升终端荷载的关系，得到水平力计算公式。

1 四角罐道水平力现场测试

1.1 测试煤矿概况

陕北大海则煤矿矿井设计生产能力为20.00 Mt/a，主井井筒净直径∅9.6 m，垂深675 m，采用两对立井提升容器提升设备，提升容器总质量74 t，提升容器名义载煤量50 t。

四角罐道的平面位置如图1所示，提升容器通过自身的金属滑靴与四角罐道发生碰撞。图1中y方向对应提升容器在停罐加卸载过程中，提升容器内进出物资方向。

图1 四角罐道示意

1.2 测试方案

采用了动态测量方式，对四角罐道受到水平力作用时的振动加速度及应力应变进行实时测试。测试系统主要包括IEPE型三向加速度传感器、120-3CA型三向免焊接应变片、DH5922D高速数据采集分析仪和220V交流电源。

现场测试时，依据提升容器的运行特征，可将提升工况分为提升容器上行进入四角罐道、停罐加卸载、提升容器下行离开四角罐道。加卸载工况中，把测试仪器布设在提升容器上、中、下盘对四角罐道的固定撞击点展开测试。在上、下行工况中，提升容器在四角罐道区域以3 m/s的平均速度低速滑行，主要将测试仪器布设在四角罐道的跨中位置和悬臂梁位置展开测试。

1.3 测试结论

经现场测试，得到作用四角罐道水平力特性。主要包括以下几条测试结论：

1)水平力为低频冲击荷载，荷载作用频率在0.19～1.27 Hz之间。当水平力的作用频率接近或等于井筒装备结构自振频率时，井筒装备结构可能发生动力失稳破坏，设计时应关注井筒装备结构及布置方式。

2)单次提升工况测试组中，提升容器会多次撞击四角罐道从而产生侧面水平力峰值Px，max与正面水平力峰值Py，max，且二者是同时出现的。

3)提升容器在停罐加卸载工况下作用于四角罐道的水平力峰值要远大于其在上、下行工况下作用于四角罐道的水平力峰值。

4)在加卸载工况中，提升容器下盘滑靴作用于四角罐道的水平力峰值大于上、中盘滑靴作用于四角罐道的水平力峰值。

基于上述测试结果，四角罐道水平力分析时，可将低频冲击荷载转化为等效静力，并分析得到加卸载工况时，提升容器下盘滑靴撞击四角罐道正面引起的水平力峰值与提升终端荷载的关系。

2 四角罐道水平力公式选型

目前煤矿立井四角罐道水平力计算无文献报道。四角罐道水平力的确定需参照端罐道设计理论[10-13]。目前主要有“西德公式”和“中矿大公式”两个理论公式可供参考。

2.1 西德公式

20世纪初德国提出的水平力经验公式：

Py=Q/12

(1)

式中，Py为罐道与罐道梁正面水平力标准值，kN；Q为提升装备终端荷载，kN。该公式适用于提升载重小于300 kN，上、下行速度小于14 m/s的提升工况[14-16]。

该公式是目前我国《煤矿立井井筒及硐室设计规范》[1]中推荐使用的端罐道水平力计算公式。该公式所适用的提升载重较小，在大载重条件下是否适用值得商榷。另外，端罐道使用工况中，提升容器是高速运动中的，这也与四角罐道主要分析停罐后装卸载条件下的受力工况有所差异。

2.2 中矿大公式

中国矿业大学经大量实测和总结，回归分析提升速度v、提升装备终端荷载Q对水平力的影响，采用最小二乘法分析水平力，得出了三参数水平力计算公式[17-19]，即：

Py=0.35avQ0.25

(2)

式中，a为动静比，建议取2.5。该公式得到了广泛的使用和推广，能较为准确地反映在高速上、下行过程中，提升容器作用端罐道水平力的基本规律。

该公式引入了动静比的概念，能更准确的反应端罐道的受力特点。另外，该公式考虑了提升速度的影响。对于四角罐道来说，当加卸载工况时提升速度为0，此时应忽略速度项，仅代入提升终端荷载进行计算。则“中矿大公式”可以简化为：

Py=7/8Q0.25

(3)

2.3 公式分析及选型

因四角罐道与端罐道的上、下行工况存在较大差异。因此，端罐道设计理论是否能够运用于四角罐道值得商榷。依据现场测试的数据，将上述两种水平力公式得到的水平力计算值和现场实测值进行对比，见表1。

表1 陕北大海则煤矿水平力实测值与计算值对比

表1显示，西德公式和中矿大公式确定的水平力计算值与现场实测值之间均有较大误差。西德公式计算值大于实测值。相对误差介于50.5%～52.7%之间，在1倍左右。说明若按西德公式计算四角罐道受力偏于安全，但过于保守。中矿大公式计算值远小于实测值。相对误差在-842%～-927%之间。这主要是由于提升速度的影响被忽略。说明由于两者的测试工况不同，导致使用中矿大水平力公式对作用四角罐道的水平力进行计算时，计算值远小于水平力实测值，与实测值出现较大误差。

考虑到采用上述两种主流的端罐道水平力计算公式进行计算时，其计算值与实测的四角罐道水平力均存在较大误差。且端罐道的测试工况与四角罐道存在较大差异，无法直接借用端罐道的水平力计算公式估算四角罐道的水平力，故四角罐道的水平力计算公式需另行分析。

通过分析中国矿业大学与西德水平力计算公式可知，当忽略速度的影响时，作用于提升容器正面的水平力Py随终端荷载Q的变化均采用幂函数形式，即：

Py=βQα

(4)

式中，α、β为经验系数。对于西德公式，α取1，β取1/12；对于中矿大公式，α取0.25，β取7/8。那么在计算四角罐道水平力时，也考虑采用相同的函数型式。为方便分析，可对该式两边取对数，得：

lnPy=lnβ+αlnQ

(5)

式中，lnPy与lnQ呈线性变化关系。本文据此，研究建立提升容器作用于四角罐道水平力计算公式。

3 四角罐道水平力计算

3.1 正面水平力Py计算

考虑到陕北大海则煤矿实测水平力数据中，提升容器在停罐加卸载时，其下盘滑靴作用于四角罐道正面的水平力为发生水平力峰值的位置。依据实测的提升容器作用四角罐道正面水平力峰值Py，max数据，将该测点的水平力峰值数据与其对应的提升终端荷载数据取对数处理，如图2所示。

图2 lnPy，max-lnQ散点图

由图2可发现，lnPy，max与lnQ大体上呈正相关的变化趋势，但个别数据存在差异性。考虑到现场实测过程中，场地情况复杂，容器偏心情况不一致、装卸煤时笼内煤块飞溅触碰到四角罐道、多提升容器同时作业影响四角罐道结构内力变化等均可能导致部分数据出现较大偏差，故回归分析水平力计算公式时，应去除离散程度较大的数据。采用一元线性回归模型，选用80%置信区间对图2中的数据进行筛选，得到不同保证率下的水平力公式参数α、β，具体计算方法[20]如下：

对于给定的置信度1-α和对于任意的x，与x对应的Y满足：

其中，

即故对于任意的x，Y的置信区间为：

上述式中的相关参数由表2计算得出。

表2 回归参数计算公式

依据计算结果，得到80%置信区间的取值范围，选取在区间内的数据进行回归分析，得到图3所示的拟合曲线。

图3 80%保证率lnPy，max-lnQ回归分析计算

依据图3中的曲线拟合计算结果，可得β=2.067，α=0.439。因此，提升容器作用于四角罐道正面的水平力计算公式为：

Py=2.067Q0.439

(7)

式中，Py为作用四角罐道正面水平力，kN；Q为提升终端荷载，kN。将水平力实测值与计算值进行比较，见表3。

表3 陕北大海则煤矿水平力实测值与计算值对比

从表3中可知，基于80%保证率处理实测数据，回归分析得到的作用四角罐道正面水平力计算公式，其计算值与实测值误差不超过3%，可较准确的反应在不同提升终端荷载下，提升容器作用于四角罐道正面的水平力峰值特征。

3.2 侧面水平力Px计算

根据现场测试结果可知，四角罐道受提升容器作用时产生的侧面水平力峰值Px，max与正面水平力峰值Py，max是同时出现的。侧面水平力Px的计算可在正面水平力Py的基础上进行折减。

统计在不同测试工况中，提升容器作用于四角罐道正面和侧面的水平力峰值Py，max、Px，max，得到每组测试组中的侧面水平力峰值与正面水平力峰值的比值Px，max/Py，max。为了便于计算水平力，将作用四角罐道侧面水平力峰值与作用四角罐道正面水平力峰值之比，即水平力侧正比，记为b。计算不同分位数下的侧正比b，如图4所示。

图4 侧正比b分位数

图4中，25%分位数对应较小四分位数，50%分位数对应中位数，75%分位数对应较大四分位数。由图4可发现，提升容器作用于四角罐道侧面的水平力峰值要小于作用于四角罐道正面的水平力峰值，两者的比值Px，max/Py，max介于0.5～0.7之间，平均数为0.62，中位数为0.61。平均数与中位数接近，说明侧正比b的数据分布集中，离散程度低，可考虑采用正态分布的区间估计方式，计算得到在不同保证率下的侧正比参考值。

经过统计计算，得到了四角罐道水平力侧正比b在不同保证率下的计算结果见表4。

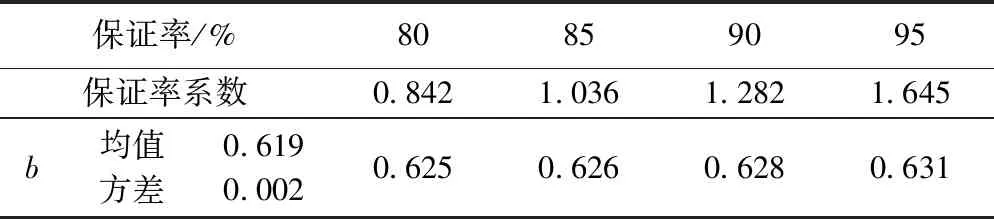
表4 陕北大海则煤矿实测数据统计计算结果

依据表4统计计算结果，取水平力侧正比b=0.628时，保证率>90%。

基于以上对比分析提出提升容器作用于四角罐道侧面水平力计算公式：

Px=bPy

式中，Px为作用四角罐道侧面水平力，kN；b为侧正比，建议b取0.628。带入相关参数，最终得到提升容器作用于四角罐道侧面水平力计算公式为：

Px=1.298Q0.439

式中，Px为作用四角罐道侧面水平力，kN；Q为提升终端荷载，kN。

4 结 语

本文基于煤矿立井提升容器在井口和井底处作用于四角罐道的水平力展开研究。依据四角罐道水平力现场测试结果，找出四角罐道的水平力特征和变化规律。通过回归分析建立提升容器作用于四角罐道正面水平力与提升终端荷载的关系，得到作用四角罐道正面水平力计算公式；通过分析水平力侧正比的测试数据关系，采用正态分布的计算方式，得到作用四角罐道侧面水平力计算公式。通过对四角罐道水平力计算方法的研究，可为井口及井底立井提升井筒装备的设计体系提供重要依据。