基于双向长短期记忆网络的煤矿瓦斯浓度预测
曹 梅 杨超宇
(1.安徽理工大学经济与管理学院 安徽淮南 232001;2.安徽理工大学人工智能学院 安徽淮南 232001)
随着我国能源需求的增长,煤炭开采量不断加大,煤矿井下环境越发复杂,安全事故频发。研究发现,在顶板、瓦斯、水害等八类煤矿事故中,瓦斯是第二大煤矿事故因素,其事故发生率为百分之二十,且波及范围广泛,危害性较高,易造成较多人员死亡[1]。因此,对煤矿瓦斯的有效预测预警,有利于煤矿安全生产工作顺利进行。关于煤矿瓦斯预测预警,学者们进行了大量研究。学者们采用灰色理论[2-5]、ARIMA时间序列分析[6]、支持向量机[7-10]、多元回归[11]和神经网络[12]等方法来研究煤矿瓦斯浓度预测。杨武艳[13]等人认为煤矿瓦斯涌出量是一种随机过程,其变化是定幅、定时的区间灰色量,使用灰色预测模型有效预测了煤矿瓦斯涌出。范京道[14,15]等人使用时间序列分析方法ARIMA模型结合SVM模型,分别预测瓦斯线性和非线性数据,对煤矿瓦斯浓度进行了有效预测。李树刚[16]等人使用RNN模型实现了煤矿瓦斯涌出浓度的预测,结果具有一定的准确性。Ping yang[17]等人利用LSTM模型,建立煤矿瓦斯涌出多步预测,结果表明,相比于ARIMA模型,LSTM模型预测效果较好。
上述方法多适合小样本、平稳性的瓦斯涌出分析,对于大样本、非线性数据波动较强的瓦斯预测效果不佳。RNN模型易发生梯度消失或爆炸的情况,造成模型精度下降,LSTM模型虽能解决RNN模型的不足,但其只能利用历史信息分析。针对上述问题,提出基于双向长短期记忆网络的煤矿瓦斯浓度预测模型,结合前向和后向长短期记忆网络,充分考虑历史和未来信息,以实际数据为基础,构建预测模型,以期有效预测煤矿瓦斯涌出浓度,为煤矿安全生产提供指导。
一、双向长短期记忆网络瓦斯浓度预测模型
煤矿井下开采环境恶劣,条件复杂突变,瓦斯浓度与煤层开采条件、采煤深度、煤层厚度、风速、CO浓度和温度等因素有关,多种因素相互作用构成煤矿井下瓦斯涌出机制系统,然而,由于井下传感器收集数据种类单一,信息有限,不能充分展现各影响因素和瓦斯涌出作用变化趋势,由此,本研究针对瓦斯浓度随时间变化的趋势,结合Bi-LSTM 人工智能算法,对煤矿井下非线性温度、风速和瓦斯时间序列大样本数据,进行实验,建立瓦斯浓度预测模型。
(一)LSTM 模型。长短期记忆(Long Short Term Memory,LSTM)网络是在循环神经网络(Recurrent Neural Network,RNN)的基础之上演变而来,改善了RNN模型缺陷,能够充分利用序列间的长期依赖关系,其基本原理采用门控机制,主要由输入门、遗忘门和输出门控制数据流,对于序列数据具有较好的处理效果。
LSTM模型内部的单元结构如图1所示,由输入门Xt、输出门ot、遗忘门ft和记忆门it组成,σ表示Sigmoid函数。
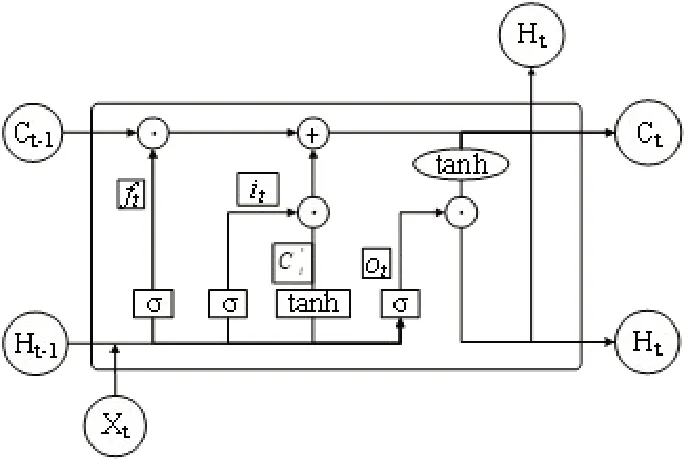
图1 LSTM单元结构
(二)Bi-LSTM 模型。双向长短期记忆(Bi-directional Long Short Term Memory,Bi-LSTM)网络是传统长短期记忆网络的一种改进。传统LSTM网络为单向网络,只能在同一个方向上移动,不能同时利用前向和后向信息,而Bi-LSTM网络结构如图2所示,结合了前向和后向长短期记忆网络的,能够充分利用输入的数据,训练序列传递时,分别在同一输出层前向和后向移动,挖掘数据之间的关联关系,增强学习能力。
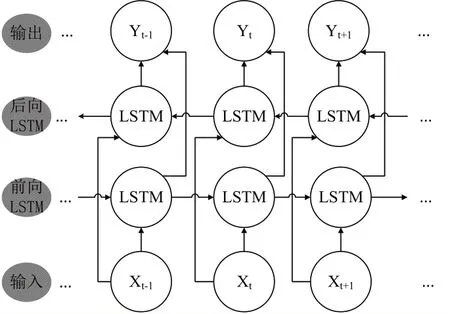
图2 Bi-LSTM网络结构
(三)基于Bi-LSTM 的瓦斯浓度预测模型。煤矿井下瓦斯涌出具有时间性,且易受多种因素影响,Bi-LSTM 网络将两个LSTM网络的前向和后向结合,充分利用历史和未来信息,对于处理复杂非线性的瓦斯序列多维数据,具有较好的处理效果。因此,为了实现煤矿井下瓦斯浓度有效预测,利用Bi-LSTM 网络,融合瓦斯、风速和温度多因素数据,遵循时间先后顺序,将数据输入到网络模型中进行训练,建立预测模型。
将处理好的时间序列瓦斯、温度和风速数据送入到Bi-LSTM网络中进行训练和预测,在Bi-LSTM网络节点中,数据经输入门传输到状态节点中,经过Sigmoid 函数和tanh函数计算,再分别依据公式(1)和公式(2)计算遗忘门和记忆门需要丢弃和保留掉的信息。
临时单元状态Ct'经过公式(3)计算并存储t 时刻瓦斯、温度和风速数据的临时状态信息,在完成信息记忆和更新之后,输出门根据公式(4)计算出当前控制单元中有多少信息能够被输出到Ht中,并作为下一时刻的输入。
单元状态Ct和隐藏层的状态节点Ht信息依据公式(5)和(6)计算得出。
Bi-LSTM模型预测瓦斯浓度的总体流程如图3所示,首先,对收集来的瓦斯及相关数据进行数据预处理,整合和处理缺失值;然后,利用最大最小归一化方法处理预处理后的瓦斯、风速和温度数据,消除不同特征之间数量单位的影响;之后,划分数据集,分别用于训练和测试;其次,通过经验公式和实验确定神经网络隐藏层神经元数量,并以MAE和RMSE为模型训练的评价指标,建立Bi-LSTM 瓦斯预测模型;最后,利用训练好的Bi-LSTM瓦斯预测模型预测瓦斯浓度,并进行误差分析,评价模型有效性。
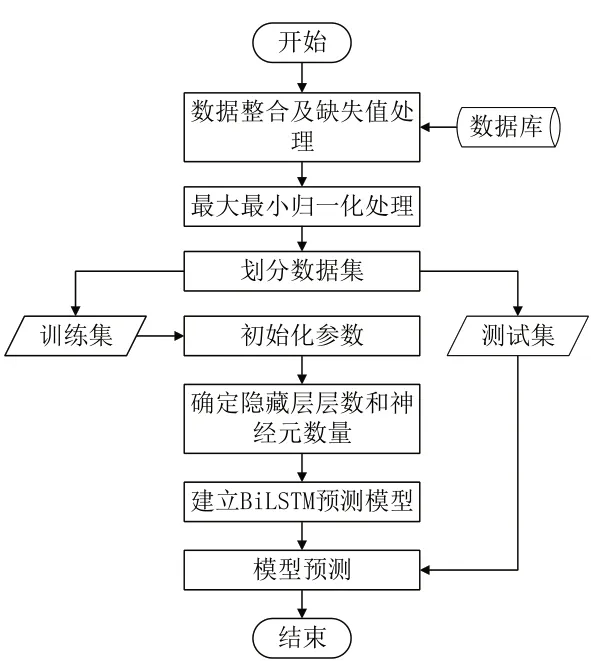
图3 Bi-LSTM瓦斯预测模型建模流程
二、数据分析及模型训练
(一)数据预处理分析。由于在数据采集过程中,煤矿井下传感器多样,数据采集种类复杂,可能会出现数据类型不一和缺失的情况,因此需要进行数据预处理,整合数据和插补缺失值。
1.数据整合。对煤矿井下传感器收集来的原始数据,进行分类、去除无效信息和合并,实验选择煤矿井下瓦斯浓度、温度和风速为模型数据样本,将其按时间顺序进行分类整合。
2.数据缺失处理。由于煤矿井下不确定因素影响,导致采集过程中数据出现缺失的情况,若将这些缺失数据删除,会造成数据不完整,丢失重要信息,不利于模型学习,因此,需要对缺失数值进行补全。选择KNN算法对缺失数据进行插补,通过公式(7)计算出缺失值xvi和其他数据xui之间的距离D,然后利用公式(8)计算出缺失值,其中wvi为与缺失值k 个近邻数据的权重,R为计算出的缺失数值。
实验所用数据来源于贵州省某煤矿采煤工作面自2021年1月14日至2021年4月9日的瓦斯、温度和风速数据,进行数据整合和缺失数据插补处理,预处理后数据的前5条和后5条如表1所示。
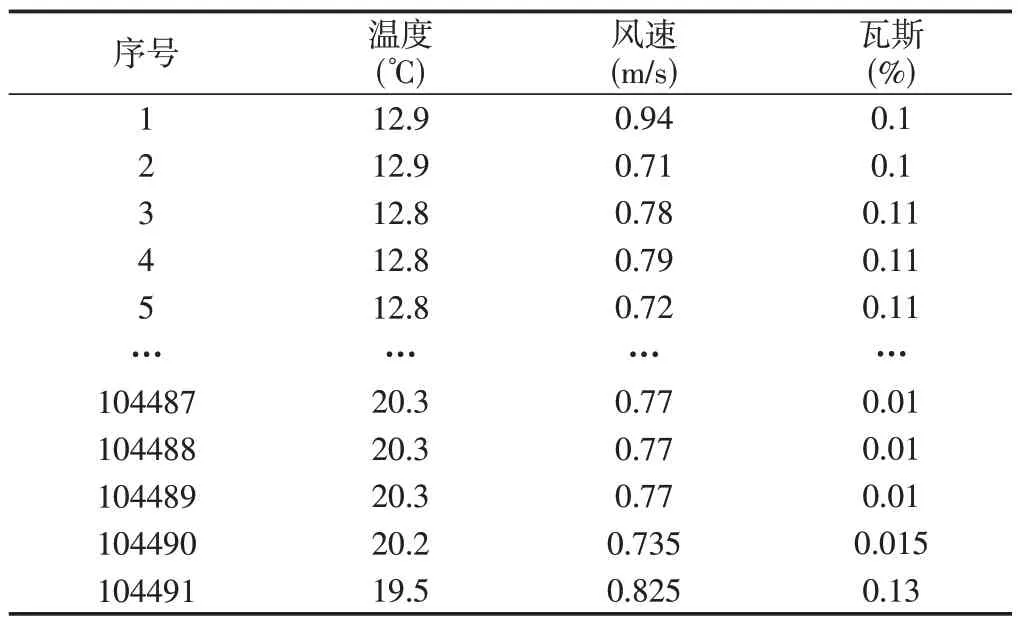
表1 预处理后数据
(二)归一化处理并划分数据集。
1.归一化处理。由于数据样本涉及瓦斯、温度和风速,其数据范围大小不同,度量单位也不一样,因此,为了消除不同变量纲量的影响,便于比较和分析,对瓦斯、温度和风速数据归一化处理,其计算公式如下:
在公式(9)中,Xmin为数据列最小值,Xmax为数据列最大值,X'为处理之后的数值。归一化处理后得到的瓦斯、温度和风速的前5条数据和后5条数据,如表2所示。
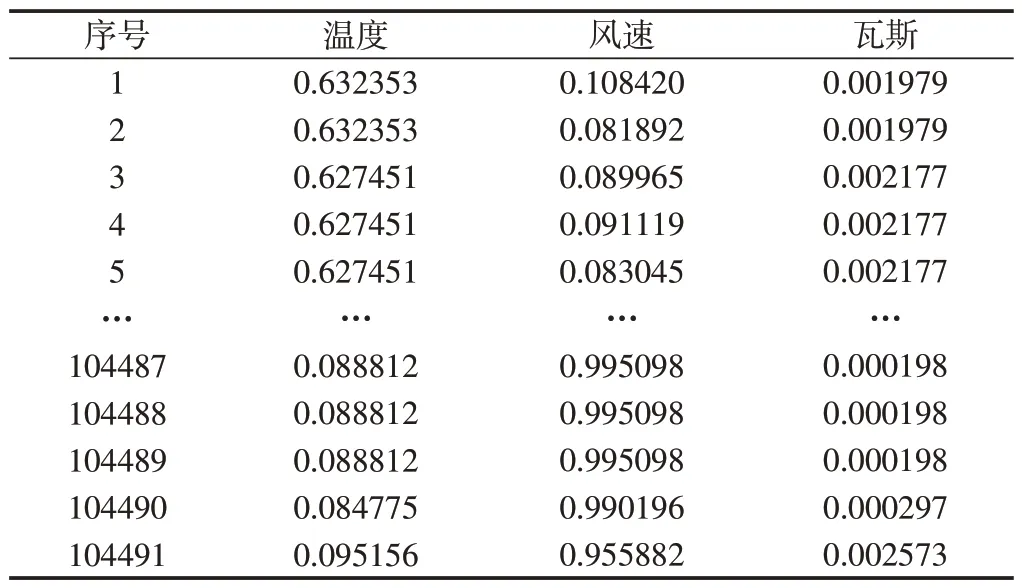
表2 归一化处理后数据
2.在对数据样本建模之前,为便于建立合适的模型,需划分数据集,一部分用于训练模型,寻找超参数,建立合适瓦斯预测模型;另一部分用于测试验证模型准确性并进行预测。按照瓦斯、温度和风速数据时间顺序,将时间序列前80%的数据用作训练集训练模型,其余数据用作测试集测试模型效果。
(三)模型训练。基于双向长短期记忆网络的煤矿瓦斯浓度预测模型基于Python3.6 语言,使用TensorFlow2.0 环境下的Keras库来完成模型的训练。
1.初始化模型参数。在神经网络中,参数的设置影响着神经网络准确性,而合适的参数设定没有固定方法,需要根据经验和实验不断试错来确定。双向长短期记忆网络瓦斯浓度预测模型的结构为输入层、隐藏层和输出层。根据经验和实验,确定模型初始化参数,输入层输入滑动窗口为3,输入特征维度为3,输入结构为(3,3);输出层输出维度为1,输出结构为(1);隐藏层数为1层,隐藏层使用sigmoid函数作为激活函数。每次训练抓取样本量256条,训练次数150次,优化器选择Adam。
2.确定隐藏层神经元数量。根据文献[18]提出的经验公式(10),在此基础上,以MAE 和RMSE 为评价指标,进行多次实验,确定隐藏层神经元数量。公式(10)中,m为输入层维度;n为输出层维度;p为常数,通常选取范围为1到10。
利用经验公式(10),在模型初始化参数基础之上,得出双向长短期记忆网络模型隐藏层神经元数量为3到13,根据公式(11)和(12),得出双向长短期记忆网络模型隐藏层不同神经元数量的MAE 误差和RMSE 误差。公式(11)和(12)中,(t)为模型预测输出值,y(t)实际数值,n为数据总量。
Bi-LSTM 模型隐藏层不同神经元数量的MAE 和RMSE 误差分析如图4 所示,隐藏层神经元数量3 至13 的MAE 平均为0.929%,RMSE 平均为0.117%,MAE 和RMSE 均低于平均值的神经元数量为8和11,相比于隐藏层神经元数量为11时,隐藏层神经元数量为8时的MAE减少0.072%,RMSE减少0.01%,因此,Bi-LSTM模型隐藏层神经元数量确定为8。
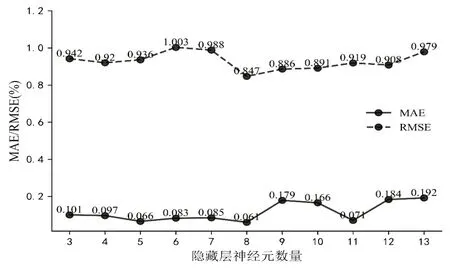
图4 隐藏层神经元误差分析
三、实验与结果分析
模型实验数据经数据整合和缺失数据插补处理后,得到有效时间序列数据共计104491 条,其中,前83590 条时间序列数据为训练数据,后20897条时间序列数据为测试数据。
(一)不同模型预测性能对比。为了验证模型的有效性,选取了相同参数下的LSTM 模型、RNN 模型和全连接(Full Connection, FC)神经网络模型,将四种模型运行结果和原始数据对比分析。图5为四种模型在测试集上的预测效果。
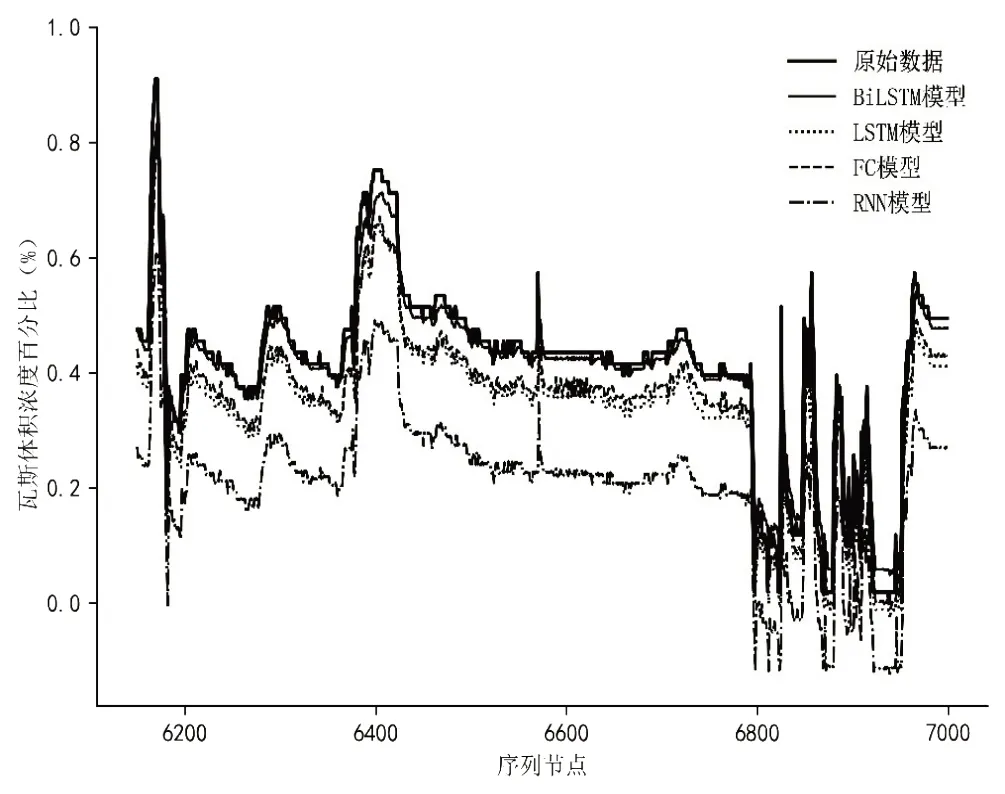
图5 四种模型预测性能对比
由于样本数据量较大,图5只展示了第6200条至第7000条数据的实际值和预测值,图中显示,四种模型均对瓦斯浓度的时间变化趋势做出了相应预测,但LSTM 模型、FC 模型和RNN模型预测较差,Bi-LSTM 模型对于瓦斯浓度峰值预测更好,预测曲线更加贴近原始数据曲线,预测效果更好。
为了更清晰地比较几种瓦斯预测模型的有效性,采用MAE、RMSE和运行时间进一步评价模型预测效果。各模型在测试集上的预测误差和运行时间如表3所示,四种模型中,Bi-LSTM 模型的MAE 比LSTM 模型和FC 模型均降低了66.7%,比RNN模型降低了72.3%;Bi-LSTM模型的RMSE比LSTM模型降低了2.6%,分别比FC模型和RNN模型降低了7.6%和4.7%,由此可知Bi-LSTM模型的准确性更高,预测效果更好。就模型运行时间来看,Bi-LSTM 模型运行时间最长,其次是LSTM 模型,FC模型运行时间最短。模型运行时间受模型的本身复杂程度影响,四种模型中,Bi-LSTM模型复杂程度较高,导致其耗时较长,但模型学习效果更好,预测精度更高。结合图5和表3分析可得,相比于LSTM模型、FC模型和RNN模型,Bi-LSTM模型虽运行时间较长,但是模型的误差较小,准确性更高,能够实现煤矿瓦斯浓度的有效预测。
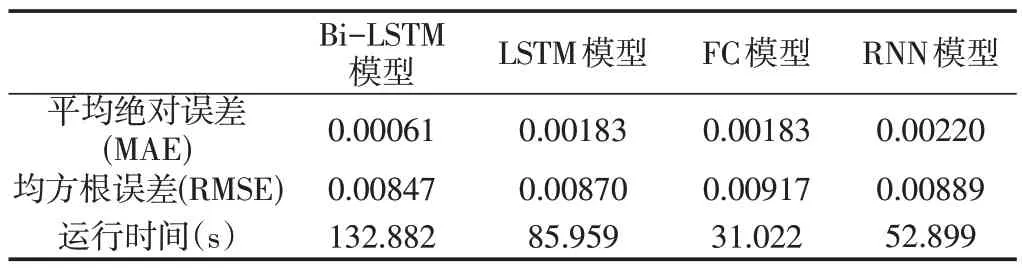
表3 各模型预测误差及运行时间
(二)Bi-LSTM 模型瓦斯浓度多步预测。为了进一步验证Bi-LSTM模型的瓦斯浓度预测性能,分别对瓦斯浓度未来时刻进行多步预测。设当前时刻为T,预测超前5、10、15、20、25 和30步时刻的瓦斯浓度,图6为Bi-LSTM模型瓦斯浓度超前多步预测部分结果显示,图中显示,随着预测步数的增加,Bi-LSTM模型的预测曲线更加偏离原始数据,结合表4所示的超前多步预测误差可知,Bi-LSTM模型超前5步预测效果最好,随着超前时间步数的增加,数据之间时间相关性的降低,预测误差不断增加,预测精度也随之下降。
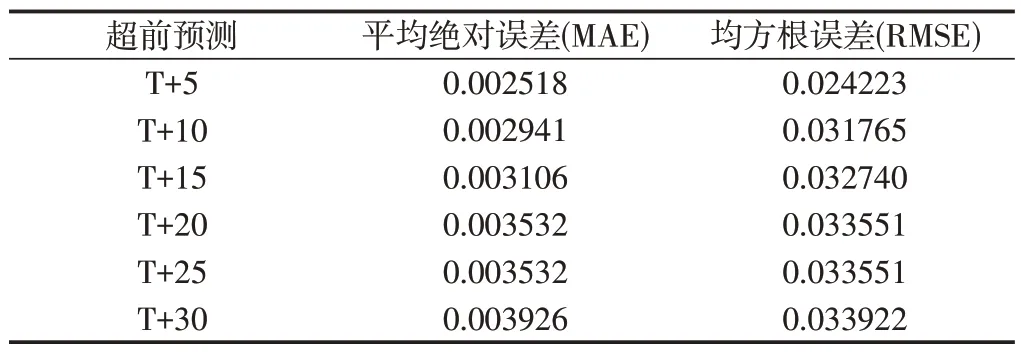
表4 Bi-LSTM模型瓦斯浓度多步预测误差
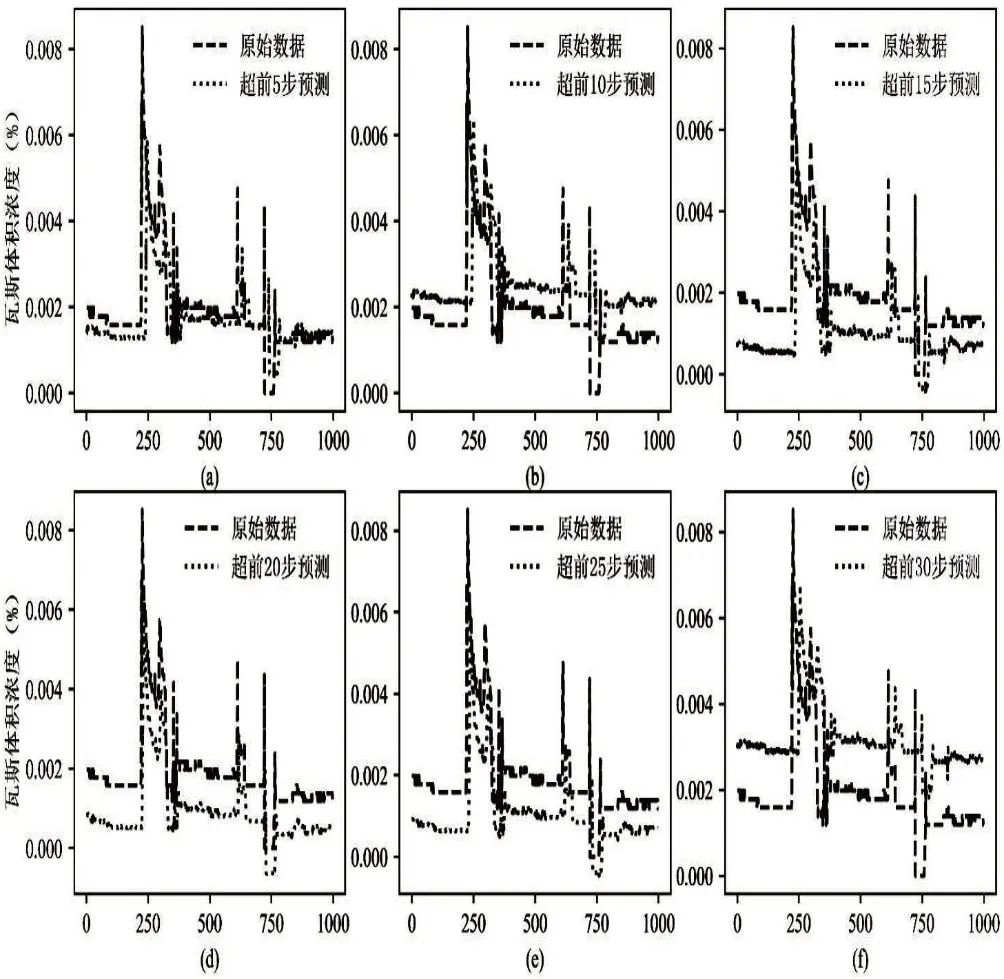
图6 Bi-LSTM模型瓦斯浓度多步预测
四、结论
利用Bi-LSTM模型进行瓦斯浓度预测,以煤矿采煤工作面瓦斯浓度、风速和温度数据为基础,通过与LSTM模型、FC模型和RNN模型比较分析,Bi-LSTM模型预测的平均绝对误差和均方根误差分别为0.00061和0.00847,预测效果优于LSTM模型、FC模型和RNN模型。
在模型预测效率方面,Bi-LSTM 模型因其结构较为复杂,运行时间较长,但其模型预测精度更高,可有效预测瓦斯浓度,为了实现煤矿瓦斯浓度的准确预测,其时间的耗费是有价值的,基于Bi-LSTM 模型的煤矿瓦斯浓度预测,能为煤矿瓦斯事故的防治提供科学的决策依据。
Bi-LSTM模型对于煤矿瓦斯短期预测效果较好,对于长期预测误差升高,预测精度下降,可能受时间关联性下降的影响,另外,煤矿井下环境复杂,瓦斯浓度不仅受到时间、温度和风速影响,还受到煤层赋存条件、开采速度、湿度等因素影响,在未来的瓦斯浓度预测研究中,应充分考虑这些因素,探究影响因素之间内在关联性,进一步提高模型预测精度。

