第五讲 中医药研究中直线相关与回归的误用分析
张婉君,姚应水
(1.安徽中医药高等专科学校 临床医学系,安徽 芜湖 241002;2.皖南医学院,公共卫生学院慢性病防制研究所,安徽 芜湖 241002)
医药统计学在中医药研究中承担着十分重要的角色,它是一种应用统计学原理和方法来分析医药数据的学科[1]。在中医药研究领域,常常需要研究两个变量之间是否存在关系,例如中草药的剂量与疗效、中医体质与疾病严重程度、中医疗法与预后等等,一般采用直线相关与回归分析来验证双变量间的关系。然而,如果不能选择正确的相关与回归分析方法,盲目套用,将会掩盖双变量间的联系,甚至带来相反或错误的结论,严重影响论文的科学性与准确性[2]。因此,本文就中医药研究中关于直线相关与回归存在的统计学问题做简要阐述与分析,以期对中医药研究者有所帮助。
1 直线相关与回归概述
1.1 中医药研究中常见的双变量相关与回归分析方法
直线相关分析方法是研究具有线性趋势的两变量是否存在关联,关联的方向和密切程度,反映两变量的相关关系[3]。对于不同的变量类型,需要选用不同的分析。若两变量属于二元正态分布资料,可选直线相关分析。例:在中药提取过程中,研究吸光度序列与提取液固体含量之间的相关性。而对于定量资料中不服从正态分布的资料,以及总体分布未知的资料和原始数据用等级表示的资料,应采用等级相关分析来描述两个变量间关联的程度与方向。例:某研究采用中药治疗重度贫血,探究患者血红蛋白含量与贫血体征的关系。而对于至少一个变量为无序分类变量的两分类变量关联性分析,应采用两种属性独立性的卡方检验。例:某研究探讨中医体质类型与胃病类型是否有关联,将收治的胃病患者按主要的中医体质类型与胃病类型两种属性交叉分类,分析中医体质类型与胃病类型间的关联。
直线回归分析方法是研究具有线性趋势的两变量间的数量依存关系,通过易测的变量对未知的或者难以测量的变量进行估计,从而达到预测的目的[4]。若两变量具有线性趋势,且满足正态分布,可采用直线回归分析。例:研究中药煎煮的相对密度与出膏率之间的关系。
1.2 直线相关与回归的基本步骤及注意事项
在进行直线相关与回归分析时,基本步骤如下:(1)首先要注意待分析的资料是否具有同质性,并且根据中医药相关专业知识来初步判断两变量间是否存在相关关系或者数量依存关系;(2)绘制两变量的散点图,观察散点的分布,判断两变量是否存在线性趋势,只有存在线性趋势才能采用直线相关或回归分析,如若发现异常值、离群值应该慎用线性相关或回归;(3)根据资料的类型特点,严格选用合适的相关或回归分析方法;(4)得出相应的统计量,相关系数、截距、回归系数等,并对其进行假设检验;(5)根据统计学结果以及相关的专业知识,得出结论并判断结论是否有实际的临床价值[4]。
此外,还应注意以下几点:(1)首先要根据专业知识考虑所作的分析有无实际意义,作直线相关与回归分析要有实际意义。当有实际意义,并且准备进行直线回归分析之前,应当先绘制散点图。如果各散点呈直线趋势,再作直线相关与回归分析。如果各散点呈某种类型的曲线趋势,则应经过变量变换,使其呈直线趋势后(称为曲线直线化),再作直线相关与回归分析,最后作相反的变换,转变成曲线回归方程。若不能使其呈直线趋势,则需用较复杂的方法直接拟合曲线回归方程;(2)适用范围:利用回归方程进行预测,一般只适用于自变量的原来观测范围或适当扩大范围,但不能随意把范围无限扩大,作回归直线时,也不可任意延长;(3)正确理解P值大小,应正确理解“P<0.01”和“P<0.05”的含义。例如对于相关系数的假设检验来说,得出“P<0.01”与“P<0.05”的结果时,其统计结论都可以认为“直线相关关系成立”,但下此结论可能出错的概率分别为“<0.01”与“<0.05”。然而,却不能得出前者比后者相关关系更密切的结论;(4)分层资料及重复试验数据的回归分析要慎重进行。能否将分层或不同批次的资料进行合并,要根据假设检验的结果来决定,差别无统计学意义时才能合并;对含有重复试验数据的回归分析资料进行回归分析时,不要采取简单化处理,要作失拟检验,即检验直线所不能解释的部分相对于实验误差来说是否具有统计学意义,若检验结果为P<0.05,就说明被分析的资料不能简单地用直线回归方程来描述。
1.3 直线相关与回归的区别和联系
1.3.1 直线相关与回归的区别 (1)在资料要求上不同:直线回归分析时,要求应变量Y服从正态分布,X可以是服从正态分布的随机变量,也可以是能精确测量和严格控制的非随机变量;相关分析中要求X、Y均为随机正态变量,即双变量正态分布。因此,能够作回归分析的资料不一定可作相关分析,但可作相关分析的资料也可进行回归分析。(2)统计意义不同:相关反映两变量间的关系是相互的,对等的,不一定有因果关系;回归则反映两变量间的依存关系,有自变量与应变量之分。这种依存关系可能是因果关系或从属关系。(3)在应用上不同:分析变量间关系的密切程度和方向时用相关,描述变量间在数量上相互依存关系时用回归。(4)取值范围不同:-1 ≤r≤1,-∞≤b≤+∞。(5)单位不同:r没有单位,b有单位。
1.3.2 直线相关与回归的联系 (1)对同一组资料,相关系数r与回归系数b的符号相同。r为正(或负)则b为正(或负),均表示与呈同向(或反向)变化。(2)同一资料相关系数与回归系数的假设检验结果是等价的,tr=tb。由于回归系数的检验过程较为复杂,而相关系数的检验过程简单并与之等价, 故在实际应用中常用相关系数的检验来代替回归系数的检验。(3)可以用回归解释相关。r的平方称为决定系数,其计算公式为:
说明当SS总不变的情况下,回归平方和的大小决定了相关系数的大小,r2反映出回归平方和在总平方和中所占的比重。r2越接近1,表示相关和回归的效果越好。如某资料r= 0.2,P<0.05 ,可认为两变量相关有统计学意义,但r2= 0.04,说明SS回在SS总中仅占4%,所以两变量间的相关关系实际意义并不大。
2 中医药研究中直线相关与回归分析的常见问题及解析
2.1 未考虑资料特点,误用等级相关
例1:某研究为探讨中医证型分布与胃病类型的相关性,作者纳入了158 例胃病患者,收集了不同中医证型的胃病类型情况,见表1。
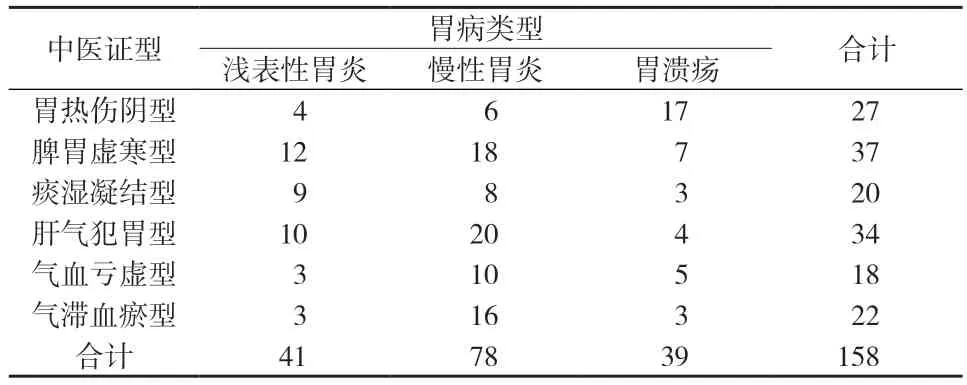
表1 中医证型与胃病类型的关系
原分析:采用等级相关分析中医证型与胃病类型的关系,结果显示,等级相关系数rs= -0.135,P>0.05,认为中医证型与胃病类型之间无相关关系。
解析:本研究的目的是研究中医证型与胃病类型的关系,收集的胃病类型分为浅表性胃炎、慢性胃炎、胃溃疡,为无序分类变量;中医证型分为六大类,分别为胃热伤阴型、脾胃虚寒型、痰湿凝结型、肝气犯胃型、气血亏虚型、气滞血瘀型,也为无序分类变量。因此,该研究属于双向无序分类资料,分析两变量间是否存在关联,一般是根据两分类变量交叉分类计数所得的列联表做关联性分析,采用行×列表资料的χ2检验,并计算列联系数,分析关联的密切程度。原分析未考虑资料的特点,而对该资料采用等级相关来分析显然不合理。因此,该研究应采用行×列表资料的χ2检验,并计算列联系数,来分析中医证型与胃病类型的关系。
2.2 未绘制散点图,直接进行直线相关或回归分析
例2:某研究探讨痰湿质女性孕晚期BMI 与血清维生素A 水平的数量依存关系,收集了20 名孕晚期孕妇的BMI 以及血清维生素A 水平检测情况,见表2。
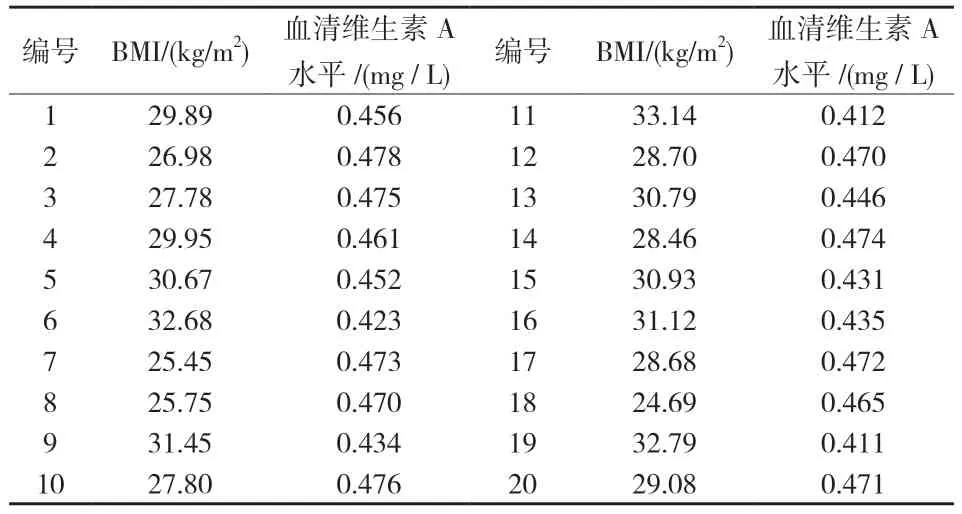
表2 痰湿质女性孕晚期BMI 与血清维生素A 水平
原分析:对两变量进行直线回归分析,结果表明,回归系数的估计值为-0.008,经t检验,P< 0.001;回归方程为Y= -0.008X+ 0.682,r2= 0.706。
解析:本研究是直接对BMI 与血清维生素A 水平进行直线回归分析,这一做法是不合理的。根据本例的原始数据,绘制散点图,见图1,观察到散点的分布呈明显的曲线趋势,显然采用直线回归分析是不合理的。因此,在进行直线相关或回归分析时,首先应该对两变量进行散点图的绘制,通过观察散点的分布,从而了解变量间是否存在直线趋势,才可以考虑进行直线相关或回归分析。若两变量间呈现的是某种曲线关系,则采用直线相关或回归方程来解释两变量间关系是不合理的,即使相关系数或者回归方程经过假设检验验证后显示具有统计学意义也是错误的。此外绘制散点图还有助于识别离群值、异常值,若出现个别远离众散点的异常值,应谨慎采用直线相关和回归分析。

图1 BMI 与维生素A 关系的散点图
2.3 相关系数未经假设检验,得出结论
例3:某研究探讨气阴两虚型2 型糖尿病患者血糖和血脂之间的相关性,选取50 例气阴两虚型2 型糖尿病患者,检测患者的空腹血糖、餐后2 h 血糖、总胆固醇、甘油三酯、高密度脂蛋白及低密度脂蛋白等资料,分析患者血糖和血脂之间的相关性。
原分析:采用直线相关性分析,结果显示,气阴两虚型2 型糖尿病患者的空腹血糖与总胆固醇、甘油三酯呈正相关关系(r分别为0.875、0.684),与高密度脂蛋白呈负相关关系(r为-0.589);餐后2h 血糖与总胆固醇、低密度脂蛋白呈正相关关系(r分别为0.544、0.382)。
解析:样本的相关系数r为样本统计量,只是总体相关系数ρ的一个估计值,存在抽样误差。如ρ不为零,则变量X和Y存在直线相关关系。而从总体相关系数ρ为零的总体中,随机抽取得到的一组样本,由于抽样误差的存在,其计算得到的样本相关系数r也可能不等于0,因此我们需要对相关系数进行假设检验,给出相应P值。
根据研究目的,需要先绘制散点图确定该数据满足相关分析的前提条件。由于原文中没有提供研究的原始数据,因此无法绘制散点图。假设当数据满足前提条件,且依据原始数据正确得出了相关系数时,应根据得出的相关系数和研究例数对总体的相关性进行假设检验。根据假设检验t检验的公式,并查找t界值分布表,分别得出各指标间总体相关性,结果显示气阴两虚型2 型糖尿病患者的空腹血糖与总胆固醇、甘油三酯呈正相关关系,与高密度脂蛋白呈负相关关系;餐后2 h 血糖与总胆固醇、低密度脂蛋白呈正相关关系,P值均小于0.05。同时对于相关系数的假设检验也可以查询相应的r界值表,其结果与t检验法相一致。虽得到的结论与原结论一致,但原分析相关系数未经假设检验就得出结论,这是不合理的。
2.4 相关系数过小,不能正确解释统计结果
例4:某研究探讨中药治疗接触性皮炎的疗效与血清IL-4 表达水平的相关性(用治疗后患者症状积分减少率来表示临床疗效,症状积分减少率越大,疗效越好)。
原分析:首先绘制症状积分减少率与血清IL-4表达水平两变量的散点图,结果显示两变量呈现线性趋势。采用直线相关性检验分析中药治疗接触性皮炎的临床疗效与患者血清IL-4 的表达水平的相关性。结果显示,用中药治疗接触性皮炎患者1 个月后,患者血清IL-4 的相对表达水平与治疗后患者症状积分减少率呈显著负相关(r= -0.26,P<0.05),相关程度高。这说明采用中药治疗接触性皮炎1 月后,患者血清中IL-4 的相对表达水平越高,临床疗效越差。
解析:相关系数r是表示两个随机变量之间直线相关强度和方向的统计量,它没有单位,取值范围为-1 ≤r≤1。r的正负值表示两量之间直线相关的方向,即r>0 为正相关;r<0 为负相关;r= 0 为零相关。r的绝对值大小则表示两变量之间直线相关的密切程度,r的绝对值越接近于1,说明密切程度越高,r的绝对值越接近于0,说明密切度越低。该研究结果中,r= -0.26,r的绝对值并不接近1,可以认为患者血清IL-4 的相对表达水平与治疗后患者症状积分减少率存在低度负相关关系,但不能盲目将两变量的相关关系解释为密切相关,显著相关或者相关程度高。
2.5 直线回归分析不考虑观测值范围,盲目外推
例5:某研究探讨中药汤剂相对密度的预测区间的数学模型,建立中药汤剂校正的相对密度与出膏率的线性回归方程,用于预测中药汤剂的相对密度,为中药汤剂的质量控制提供一定的科学依据。
原分析:首先对两变量进行散点图的绘制,观察两变量呈现线性趋势。通过建立直线回归方程用出膏率来预测中药汤剂的相对密度,结果显示校正的相对密度(Y)对出膏率(X,%)的直线回归方程为:Y= 0.000 4X+1.000 3,r2= 0.967。并对直线回归方程进行假设检验,得P<0.01,可认为校正的相对密度与出膏率之间有线性关系,直线回归方程成立,可利用方程来预测中药汤剂相对密度。
解析:原分析中未给出线性范围并认为可利用方程来预测中药汤剂相对密度。在直线回归分析的过程中,需要警惕过度外推。当利用现有的解释变量X值获得的回归直线,来预测那些超出现有的解释变量X值范围的反应变量Y值的情况时,一定要谨慎。例如在该研究中,利用回归方程进行预测时,能否据此预测某种中药出膏率为0.1%时,该中药的相对密度?理论上似乎可以将0.1%代入回归方程,得到相对密度的预测值为1.000 3;出膏率为0.1%已经超出了数据范围,此时不能保证中药种类中是否确实存在如此低的出膏率以及当出现如此低的数据时,两变量间是否还具有同样的线性关系,故这个结果是不可信的。因此,在直线回归分析前应确定自变量的取值范围,适用范围一般以样本数据中的自变量取值范围为限,即不要超过样本数据的自变量取值范围计算值;外推得越远,其变量间的关系可能越不合理。
2.6 非正态分布的资料,误用了直线相关分析
例6: 某医师采用某中药配方颗粒剂治疗某病患者,测得一组患者血小板数及出血程度的资料如下表3,试分析两者之间的关系。
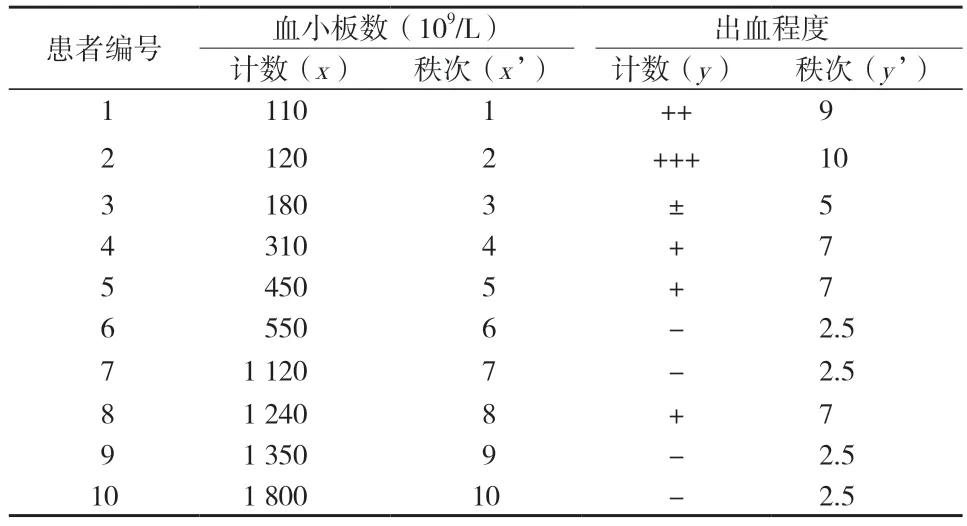
表3 10 名某病患者血小板数及出血程度数据
原分析:直接采用直线相关分析,r= -0.660,P<0.05,显然不正确。
解析:该资料出血程度属于等级资料,应当采用等级相关,等级相关系数意义同直线相关系数,其值也是波动在-1 到1 之间。其计算方法是:将成对的两组变量的观察值各按从小到大编秩,当观察值相同时,取平均秩次,然后对秩次进行直线相关分析。该资料,rs= -0.753 9,P<0.05,即某病患者血小板数及出血程度之间有负向的等级相关关系。
3 结论
直线相关与回归方法是中医药研究中常见的统计学分析方法。本文主要列举了中医药研究领域中一些常见错误案例,分析其误用的原因,并给出正确的分析。为了减少或避免误用的现象,研究者应打牢统计学理论知识的基础,提高统计学素养;并且在统计分析之前依据不同的资料类型,选择合理的统计学分析,避免盲目套用,从而提高中医药文献的科学性、准确性、客观性。

