聚类算法在大学生心理调查数据分析中的应用
许新刚,赵 燕
(徐州工业职业技术学院 信息工程学院,江苏 徐州 221140)
0 引言
新型冠状病毒感染疫情是一次全球性的事件,给在校高职大学生的学习、生活环境带来了很多的影响:居家网课、在校网课、随疫情变化的线上线下交替的新学习模式给学习带来了不适;封控隔离、出行不便等影响了学生的交际范围;病毒的变异和传染力的提升增加了对疫情的恐慌[1-4]。环境的急剧改变给入世尚浅的高职大学生的心理带来了压力。学生出现了焦虑、烦躁、易怒等负面情绪,生理上出现失眠、出汗、紧张等现象,学习过程中出现了上课不集中、记忆力下降等认知下降问题。及时了解疫情防控期间高职大学生的心理压力状态,制定合理的对策给予有效的干预释放压力,这对高职大学生的成长非常重要。
问卷调查是心理工作中获取统计资料的重要手段,既可以收集简单的人口统计信息,也可以获取体验、情感等复杂信息,通过描述性统计分析和推断性统计分析,从少量样本数据的研究得到一般性推论[5-9]。本项目采用问卷调查的方式获取疫情防控期间高职大学生的心理状态资料,研究不同心理压力状态下学习心理特征和心理调适的效果,为学校心理工作的开展提供决策依据。基于心理状态数据做交叉分析可以了解疫情防控期间学生在压力下的表现现状和产生问题的原因。为了掌握学生的心理压力状态,在问卷中设计了学生的心理状态自我评价的单选题,但部分学生因自我认识不精确等原因而在自评时未选择真实的答案,导致自评数据与学生的真实心理状况出现较大差异。当心理压力大时,学生会在生理、情绪、认知、行为等方面表现出一定的异常,通过对多维外在表现指标的综合分析能更真实地了解学生心理压力的状态。因此,问卷还设计了多个与心理压力相关的外在表现题目,如疫情防控期间的交往需求变化、饮食状况、体重变化、睡眠等。
根据学生在疫情防控期间的多个方面的外在表现数据对学生的心理压力进行测算,并按严重程度进行分组,属于广义上的分类问题,可以采用分类或者聚类算法[10-14]。但由于没有受调查者真实的心理压力数据作为训练依据,无法通过调查问卷数据建立好的分类模型来对抽样数据进行分类,分类算法无法应用于当前研究。因此,引入了无监督学习中的K-means聚类算法对调查数据进行分析挖掘,对被调查者按心理状态进行分群,提高研究的准确性。
1 调查对象和描述性分析
1.1 调查对象
采用整群抽样的方法,在徐州工业职业技术学院、江苏建筑职业技术学院、江苏安全技术职业学院、徐州幼儿师范高等专科学校、江苏省徐州技师学院5所职业院校的部分班级学生中开展问卷调查。共收回4 523份问卷,剔除不合格问卷20份,问卷有效率99.56%。其中,男生2 244人,女生2 259人。按年级统计,一年级学生1 350人,二年级学生1 606人,三年级学生1 547人。
1.2 调查方法
调查方式采用自编的调查问卷,在问卷星网络调查平台发布问卷,通过二维码的形式发给学生填写。问卷内容主要包括:(1)一般情况调查,主要是学生的基本信息,如性别、年级、是否独生子女、身体健康状态、作息规律等;(2)新冠疫情带来的心理压力;(3)新冠疫情防控期间学习心理和学习状态;(4)疫情防控期间的心理自我调适和干预情况。问卷共设计了多选题10道,单选题37道,单选题包括有序选项和无序选项两类,问卷采集的数据均为定性数据。
1.3 调查数据的描述性分析
问卷对被调查学生的健康状况进行了自评调查,非常健康的学生比例为62.11%,比较健康的学生比例为34.53%,绝大部分学生的健康状况是良好的。疫情的长期存在给学生的心理带来了一定的影响,70.97%的学生表示有影响,其中9.06%的学生表示影响较大。新冠疫情传染力强、破坏力大,被调查学生中有近30%的学生表示对于新冠疫情具有恐惧心理,男生、女生在对疫情的恐惧心理方面有差异,对疫情有恐惧心理的学生中女生的比例更高,如表1所示。

表1 对新冠疫情恐惧心理调查数据分析
新冠疫情给43%的被调查学生带来了心理压力,其中4%的学生感受到压力比较大;男生和女生的心理压力状况存在差异,男生心理压力较大的占比更高,如表2所示。由于疫情封控的影响,45.53%的学生表示疫情造成了社会交往的短缺,56.58%的被调查学生表示疫情防控期间存在沉迷网络、生活不规律的问题,如图1所示。
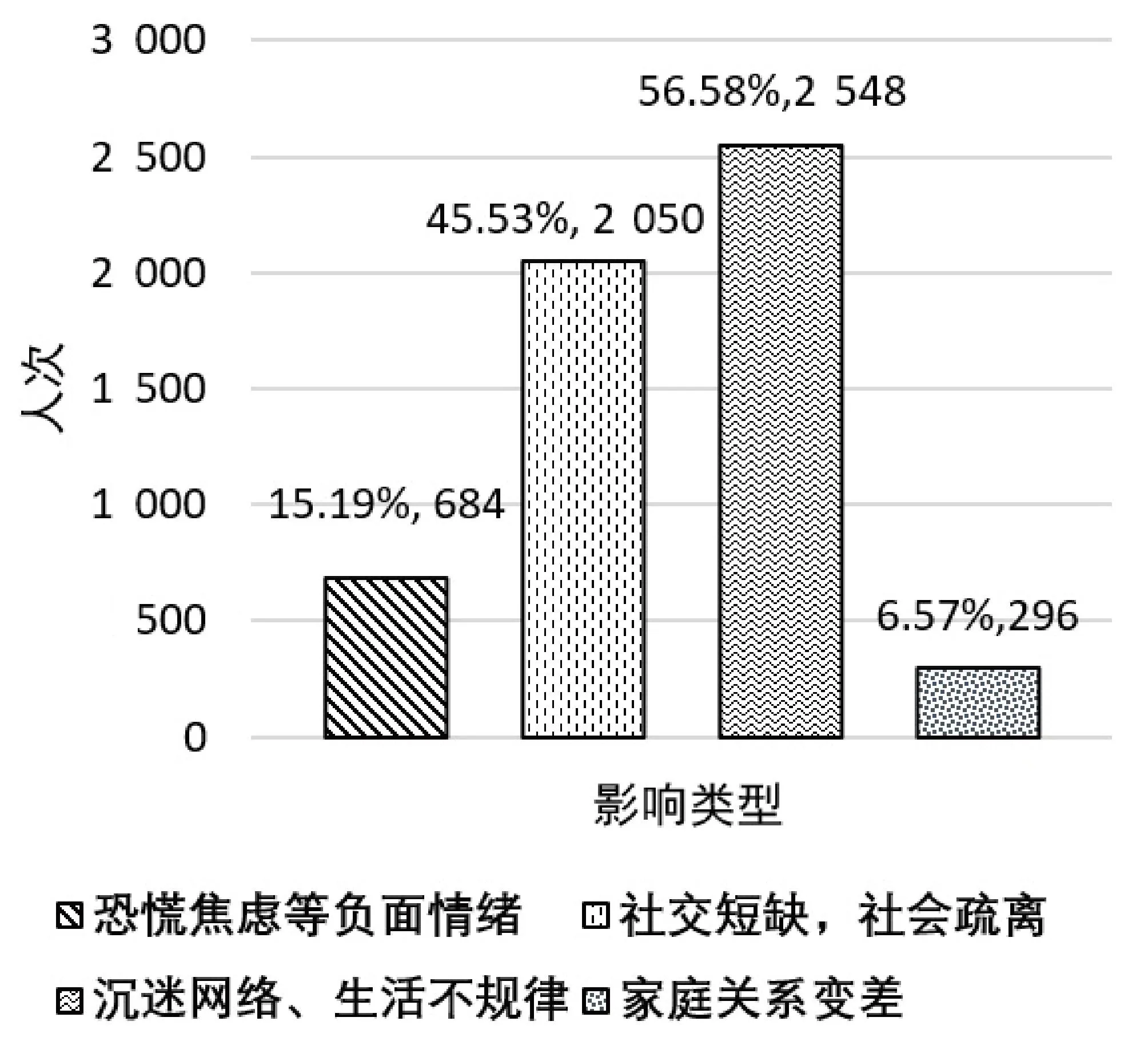
图1 疫情带来的影响

表2 新冠疫情带来的心理压力程度调查数据分析
2 心理调查数据K-means聚类分析
2.1 K-means聚类算法
聚类是一种无监督分类方法,在没有给定划分类别的情况下,根据数据间的某种相似度将数据对象归并到不同的簇。与分类算法不同,聚类算法不需要事先拥有具有类别标记的训练样本就可以对数据对象进行分组。疫情防控期间学生心理健康的调查采用网络匿名的方式进行,没有开展实名求证调查,所有学生的心理健康状况是未知的,建立分类模型较困难。采用分类算法研究学生不同心理健康状况下的行为、心理压力特征是个难题,而聚类算法恰好可以解决这个难题。聚类算法有很多种,常用的有划分类算法、层次聚类、基于密度的聚类算法、基于模型的聚类算法等。K-means算法是典型的基于距离的聚类算法,将具有n个数据的数据集dataSet={X1,X2,X3,…,Xn},根据样本间的距离大小划分为k个簇。算法流程如下:
最后是用典手法的使用。此处的典故使用主要还在“先天下/后天下/黄金屋/颜如玉”一句上,具体分析见上文。另一处并不很明显,主要是通过提取“沽”和“酒”二字反应,此处当是“沽酒当垆”之典故的运用。运用卓文君、司马相如当街卖酒的典故可以说是具有反讽味道的,更显现出秀才的逃避与对妻子的不公。
(1)数据集成,将各种类型数据转变成可以挖掘的数值型数据,每个点的数据是由多个属性变量组成的向量Xi=[xi1,xi2,…,xij,…,xim]。
(2)创建k个空簇,从数据集中随机找k个数据E1,E2,…,Ek作为这些簇的初始质心。
(3)分别计算每一个数据Xi与k个质心的距离,找到距离该数据最近的质心,将该数据划分到这个质心对应的簇中。
(4)分簇结束后,比较前后两次获得的分簇结果:若结果一样或者达到预设的最大迭代次数,则终止计算。若结果不一样,计算每个簇中所有点的均值作为新的质心,重复3~4步骤直至满足迭代截止条件。
K-means算法以距离作为相似度指标,常用的距离有欧几里得距离、曼哈顿距离和切比雪夫距离等。其中,欧式距离是常用的指标,假设有n个样本数据,每个数据有m个属性,样本数据是一个n×m矩阵。则其中两个点Xi和Xj间的欧式距离为:
(1)
迭代截止条件采用距离的误差平方和SSE:
(2)
当误差平方和不变时,迭代计算截止,获得了本次聚类的最优解。同时,也可以用SSE衡量不同聚类结果的优劣,多个聚类结果中选择SSE较小的一个。
K-means算法以距离作为相似度指标进行分类,迭代结果收敛于局部最小值,同时聚类的结果与初始质心的随机选择相关,不同的初始质心得到的结果可能不同。为了克服经典K-means算法这些缺点,二分K-means算法被提出,该算法最初是将所有数据初始化为一个簇。首先将初始化的簇分裂为两个簇,计算这两个簇的SSE指标,将SSE指标较大的一个簇再次分为两个簇,依次继续直到满足迭代终止条件。二分K-means算法的流程如下。
(1)将所有数据划分在一个簇内。
(3)计算两个新簇的误差平方和,从已有簇中选择SSE最大的簇作为指定簇。
(4)重复2~3步骤,直到簇的数目等于预先给定的K值。
2.2 学生心理状态的聚类分析
学生的心理状态常常会通过行为、情绪、生理状况等多方面表现出来,通过这些因素的综合分析可以对学生的心理健康状态进行分级。为了达到该目的,从学生的生理状态、情绪、社交等指标入手,在调查问卷设计了8个单选项目,这8个项目的问题与心理健康呈反向关系。设置的问题如:“新冠疫情防控期间,你是否感到疲倦?”,答案选项均为“(a)没有;(b)偶尔;(c)经常;(d)严重”。
对这8个项目的调查数据进行频数统计,统计结果展示在表3中。从频数统计结果可以看出,每项指标中绝大部分被调查学生的表现是正常的,出现异常的学生数量均较小。频数统计结果只能反映单指标的调查结果,未考虑多指标间的相关性,无法做多指标综合分析。也就是统计表只粗略地反映出各个指标下学生心理压力的外在表现现状,各指标正常状态数据的高占比能推断出被调查学生大部分心理健康。但反过来,各项指标中的少量异常数据不能断定学生存在着严重心理问题,只有具体某个人出现了多个指标均出现异常情况下才能推断其心理存在问题。希望在没有学生心理健康档案的情况下,从众多调查数据中找出潜在的心理健康存在问题的样本。因此,文章引入二分K均值聚类算法,利用多指标对学生心理健康状态进行分群研究。

表3 高职大学生心理健康状况调查统计 单位:人

表4 定性数据转换编码
K均值聚类算法通过计算数据之间的距离实现分类,要求输入为数值型数据,而本次问卷调查收集到的数据均为定性描述性的数据,在使用聚类进行挖掘之前必须对数据进行编码处理,以适应聚类计算机程序处理要求。在采用二分K均值建模时,将提取的8个项目数据按严重程度赋予不同的分值转换为数值型数据:“没有”“偶尔”“经常”“严重”分别用0、1、2、3代替,将定性描述数据转换为数值型数据,每个被调查学生的数据由8个取值范围0~3间的整数组成,如某个同学的8个指标数据转换为[1,0,0,1,1,0,0,0],根据非零数据对应的指标进行解译就是该学生偶尔感到疲倦、交往需求减弱、注意力不集中,其他指标正常。
根据以上8个项目指标将学生分为4个群组,分别与心理非常健康、一般健康、亚健康、心理压力大四种状况相对应的。因此,首先设k=4,利用Python语言编写的二分K均值聚类分析程序对被调查学生进行聚类分组,经过3次分裂后,输出最终的各簇质心坐标和分类结果。表5为4个簇的质心坐标,这些数据是数学运算的结果,是实数,若要其具有实际意义,必须将其取整。将质心坐标四舍五入取整。

表5 k=4,二分K均值聚类各簇的质心坐标
(1)簇1的质心坐标为[0,0,0,0,0,0,0,0],说明被调查学生均未出现8个负性指标描述的异常状况,心理非常健康。
(2)簇2的质心坐标为[1,0,0,0,0,0,0,0],被调查学生除了偶尔感到疲倦外,均没有其他7个指标描述的状况,心理健康情况较好。
(3)簇3的质心指标为[1,0,1,1,1,1,1,1],被调查者除了没有自杀倾向外,其他7个指标描述的状况偶尔都会出现,说明心理健康情况存在轻微问题。
(4)簇4的质心指标为[2,1,1,2,2,2,2,2],被调查对象经常会出现指标描述的异常情况,心理压力较大。
对聚类结果进行统计,归于簇1~4的数据分别有2 799、803、740、161组,占比分别为62%、18%、16%、4%。从聚类结果看,80%的被调查学生的心理健康状况较好,16%的学生的心理健康存在轻微问题,需要给予一定的关注。而对于簇4中出现的被调查者,8个负性指标描述的异常状况在他们身上经常出现,说明他们的心理压力较大,对于这些同学要给予重点关注,给予必要的心理危机干预,使其向良性转变。
对k=4时的聚类结果进行分析,其中簇1和簇2在8个负性指标方面的差异较小,仅在“感到疲倦”这一个指标出现少量的差异,将其归为一类更合理。据此将簇数k设为3,再次进行聚类分析,获得的各簇质心坐标如表6所示,簇1、2、3分别对应心理健康、亚健康、心理压力大。对聚类结果进行统计,簇1、2、3分别有3 602、740、161组数据,占比为79.99%、16.43%、3.58%,与k=4的聚类统计结果较为吻合。基于以上8个指标的调查数据聚类分析,簇数3是最佳的。

表6 k=3,二分K均值聚类各簇的质心坐标
3 心理调查数据聚类结果讨论
3.1 数据一致性分析
将k=3聚类结果与学生对疫情是否带来压力的自我评价结果进行比较,从中可以发现部分学生的自评结论和其外在表现存在一致性问题。表7中展示了部分调查数据,A~H 8个指标和自评结果都反映疫情防控期间学生心理压力程度,对其一致性进行检查:34号问卷的学生自评没有压力,但是从8个指标上看其经常感到疲倦、交往需求减弱和严重的无助感,其他指标也偶尔发生,从这些表现看其不可能没有心理压力。386号问卷的学生中8个负性指标均属于比较严重级别,但自我评价是没有压力。3325、3696号问卷学生除了偶尔疲倦这一指标外,其余均是“没有”,从8个指标的外在表现推断心理压力应该极小,但其自评却是“压力较大”,自我评价结果的可信性存疑。

表7 调查数据一致性分析(部分)
3.2 基于自评和聚类结果的调查数据对比分析
基于k=3的聚类分析结果,将被调查者分为3个群,分别对应心理健康、亚健康、心理压力大。基于学生自我评价的心理压力分组和聚类分组结果,研究不同心理压力状态的学生的作息规律特点。表8为作息规律-心理压力(自评)进行交叉分析的结果,从表中可以看出心理压力较大的学生组中作息规律“完全不规律”和“不怎么规律”的总占比为20.20%,有一些压力的学生组中这两项占比为19.45%,没有压力的学生组中占比为10.17%。作息不规律(包含“完全不规律”和“不怎么规律”)和作息规律(包含“非常有规律”和“比较有规律”)人群的心理压力特征有显著差别(p<0.05):压力较大人群中生活不规律者的占比(20.20%)要高于平均水平(14.24%)。

表8 作息规律-心理压力(自评)交叉分析
表9为作息规律-心理压力(聚类)交叉分析结果。从表中可以看出心理压力较大的学生组中作息规律“完全不规律”和“不怎么规律”的总占比为52.17%,亚健康的学生组中这两项占比为26.08%,没有压力的学生组中占比为10.11%。作息不规律(包含“完全不规律”和“不怎么规律”)和作息规律(包含“非常有规律”和“比较有规律”)人群的心理压力特征有显著差别(p<0.05):压力较大人群中生活不规律者的占比(52.17%)要高于平均水平(14.24%)。
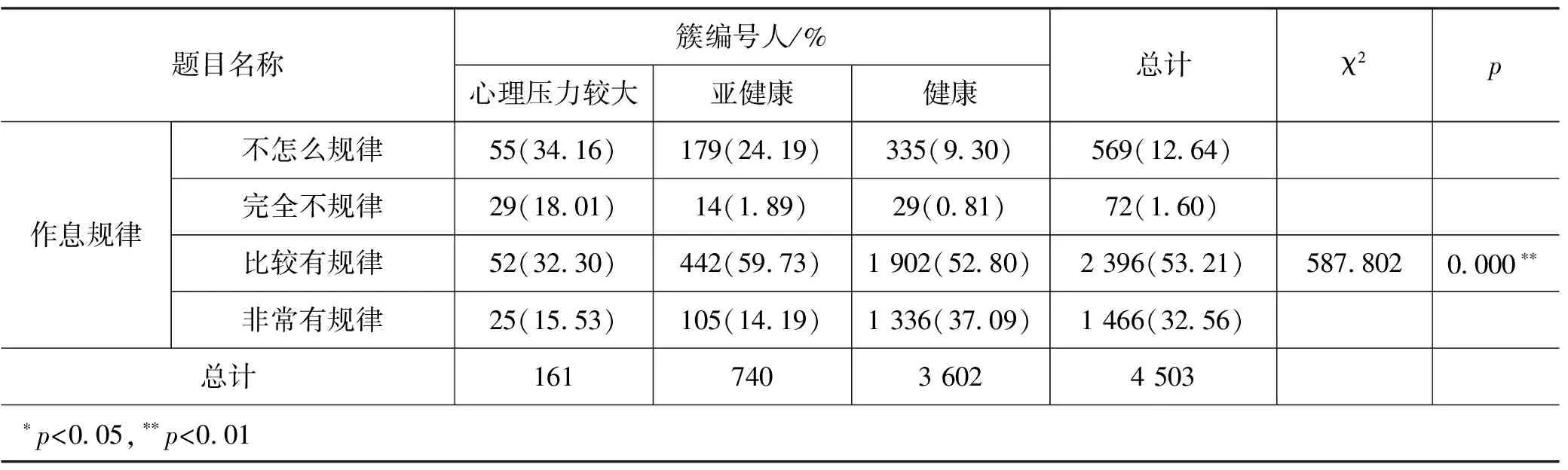
表9 作息规律-心理压力(聚类)交叉分析
从二者的分析结果可以看出,生活规律者和不规律者的心理压力状态均具有显著的差异,即心理压力较大人群中生活不规律的占比要高于心理压力较小人群。但通过聚类算法得到的群组中,心理压力较大人群中存在生活不规律现象要远高于自评分组。生活不规律者中心理压力大占比更高的结论更符合实际,可见聚类分组效果更好。
4 结语
针对学生对于自己心理压力的自我评价主观性太强导致问卷调查统计结果出现偏差问题,文章提出了基于K-means聚类算法的多维指标综合分类方法。通过疫情防控期间高职大学生心理调查实证研究,本研究对比了基于自评和聚类分组下的统计结果。对比结果表明,基于聚类算法的多维指标综合分析采用了更多的客观数据对心理压力状态进行推断,得出的学生心理压力状态较学生自我评价更客观、准确度高。研究结果证明了基于K-means聚类算法的多维指标综合分类方法在此项目中的应用是可行的、有效的。

