地理信息系统空间数据库中混合数据的近邻查询研究

杨阳

（梅州市测绘与地理信息中心，广东 梅州 514071）

1 引言

随着我国路网建设、地理位置服务等相关工作的持续完善与不断发展，空间数据库得到逐步推广和应用。为不断满足产业的发展需求，空间数据库的构建已经与物联网、机器学习、大数据等现代化技术发生一定程度的融合[1]。随着地理信息系统的不断发展，空间数据索引、混合数据检索成为数据库工作领域的研究重点[2]。相比常规的索引方式，空间数据查询具有一定的优势，能够有效提高系统对数据的访问效率与查询数据使用率。在数据索引工作持续推进过程中，有关部门提出了针对空间数据库中混合数据的近邻查询方法，该方法是数据库关键词数据检索与核心数据检索的基础[3]。由于终端用户对检索数据需求的不断改变，近邻检索被演变为最近邻检索、组近邻检索、聚类检索等[4]。但在现有检索与查询方法应用效果的深入研究中发现，大部分方法在检索中都需要将抽象的空间点、空间线段作为研究对象，即查询的目标数据集合与检索到的空间数据集合往往存在类型不匹配、格式不统一问题。

因此，为解决这类问题，充分发挥地理信息系统在测绘地理信息生产、空间数据库构建等方面的价值与效益[5]，研究以某地理信息系统为例，设计一种针对空间数据库中混合数据的近邻查询方法，为数据库的检索、查询等工作提供技术支持。

2 构建空间数据库中混合数据Voronoi 图

为满足空间数据库中混合数据的近邻查询，提取数据库的混合数据，构建对应的Voronoi图。Voronoi图一般指泰森多边形，是一组由连接两邻点线段的垂直平分线组成的连续多边形。一个泰森多边形内的任一点到构成该多边形控制点的距离小于到其他多边形控制点的距离。

在构建过程中，需要判断查询数据集合在空间中的生成对象类型与位置关系，其中，点间距离等分线是两个连线的纵向等分线，两个点之间的Voronoi图边是两个连线的竖向平分线[6]。点到线段的距离等分线属于直线段，直线段直接作用于影响区域，直线段距离相等线是以点为中心、以直线段为准线的抛物线，将其作为依据，确定混合数据Voronoi图的覆盖区域。在确定区域内点集后，按照公式（1）计算，定义混合数据Voronoi图的边。

公式（1）中：R表示混合数据Voronoi图的边；x表示空间数据库中混合数据子集；X表示混合数据集合；d表示距离；Pk表示以k为半径的外接圆；Pj表示以j为半径的内接圆。

在确定混合数据Voronoi图的所有点集后，生成并连接若干条混合数据Voronoi图的边，按照上述方式，完成混合数据Voronoi图的构建。

3 邻域点集数据精简处理

在上述设计内容的基础上，考虑到Voronoi图中的混合数据量较大，且存在数据冗余方面不足的情况，会在一定程度上影响数据近邻查询结果[7]。因此，要对数据集合进行精简处理操作。在此过程中，计算一个随机数据点距离其近邻直线的距离，计算公式如下：

公式（2）中：D表示随机一个数据点距离其近邻直线的距离；a、b、c分别表示数据点在三个方向的矢量。在此基础上，将计算得到的D作为空间数据精简邻域，将随机选择的数据点作为中心，将D作为半径，建立外接圆，从中提取邻域点集个数，此过程具体计算公式如下：

公式（3）中：p表示邻域点数据集合；N表示邻域点集个数；i表示邻域点集中第i个数据[8]。保留上述集合中的数据，同时删除空间中的其他数据将其作为冗余数据，以此种方式，完成邻域点集数据的精简处理操作。

4 混合数据KNN 查询

基于上述设计内容，引进KNN 算法。KNN 算法是一种邻近算法，或者说K 最邻近（K-NearestNeihbor，KNN）分类算法是数据挖掘分类技术中最简单的方法之一。所谓K 最近邻，意为K 个最近的邻居，说的是每个样本都可以用它最接近的K 个邻近值来代表。近邻算法就是将数据集合中每一个记录进行分类的方法[9]。设计针对地理信息系统空间数据库中混合数据的KNN查询。在此过程中，假定数据库中混合数据集合表示为Q，则混合数据KNN 查询的返回数据应为OQ，将OQ作为混合数据KNN 的查询结果。假定地理信息系统空间数据库中的混合数据维度为n[10]，则空间中随机向量的查询过程如公式（4）所示。

公式（4）中：L(q)表示空间中随机向量q的查询过程；n表示地理信息系统空间数据库中的混合数据维度；q1、q2分别表示随机向量q的两个邻近点。按照上述方式，实现混合数据的KNN 查询，以此完成近邻查询方法的设计。

5 对比实验

上文分别从三个方面，以某地理信息系统为例，设计了一种针对空间数据库中混合数据的近邻查询方法。但目前该方法的研究仍局限在理论阶段，还没有进行到实际操作阶段。本文结合研究成果，采用设计对比实验的方式，针对空间数据库中混合数据的近邻查询方法展开测试，以便将设计查询方法在测绘地理信息生产领域进行推广应用。

为满足实验需求，为地理信息系统空间数据库提供一个相对适宜的运行环境，按照表1 所示的内容，设计对比实验环境的技术参数。

表1 对比实验环境技术参数

按照表1 内容完成实验环境的布置后，选用由某地区地质测绘工程单位提供的测绘地理信息数据作为此次对比实验的测试集合，实验相关数据均存储在地理信息系统空间数据库中。实验数据为某地区地质测绘工程现场反馈数据，数据集合中包含1957027 个节点数据，共涉及2654792 条路段。为确保实验结果的真实性与可靠性，实验前要对地理信息系统空间数据库中的数据进行适当调整，可在数据集合中添加空间坐标、方向数据等信息，并在不同的测绘路段随机生成数据节点与路段。将随机生成的节点以混合数据的方式录入数据库，插入的节点与路段之间存在交叉关系，且所有线段之间均不发生交互。

完成上述准备工作后，使用本文设计的空间数据库混合数据近邻查询方法，进行混合数据近邻查询。查询过程中，先构建空间数据库中混合数据Voronoi图，对空间数据库中的混合数据进行精简处理，在此基础上，引进KNN 算法，通过对混合数据的KNN 查询，完成本文方法在实验中的应用。

为满足实验结果的对比性需求，检验本文方法与传统方法的优势与不足，引进基于数据空间自适应规则的近邻查询方法、基于本地化差分隐私算法的近邻查询方法，将上述两种方法分别设定为传统方法1 与传统方法2。实验分别按照对应方法的规范化操作步骤，进行地理信息系统空间数据库中混合数据的近邻查询。确保实验中相关参数条件不变后，将近邻查询过程中目标数据集合周围数据对象密度对CPU 运行时间的影响，作为评价本文查询方法应用效果的关键指标，由技术人员统计实验结果，具体如图1 所示。

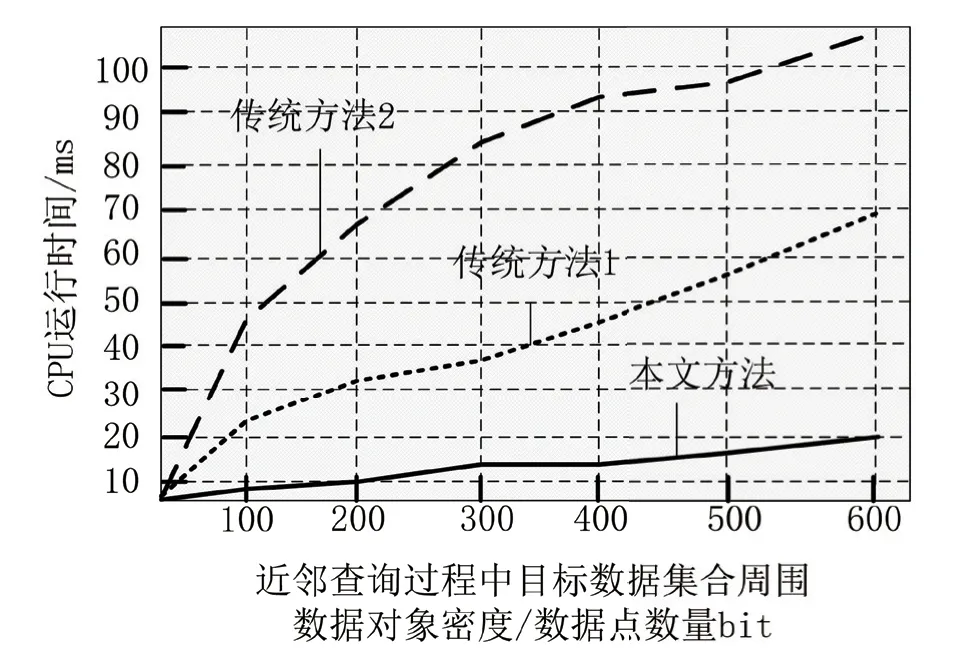
图1 近邻查询过程中CPU运行时间对比结果

从图1 所示的实验结果可以看出，在三种方法中，本文设计的方法应用后，目标数据集合周围数据对象密度对CPU 运行时间的影响最小，即在查询过程中CPU 的运行时间最短。

在完成上述设计后，按照相同步骤再次开展实验，将查询时空间数据库中的混合数据量对I/O 代价的影响作为评价指标。I/O 代价越高，说明查询所占用的CPU 越高，出现异常查询或查询中出现卡顿的次数越多；反之，I/O 代价越低，说明查询所占用的CPU 越低，出现异常查询或查询中出现卡顿的次数越少。以此为依据，统计对比实验结果，如表2 所示。

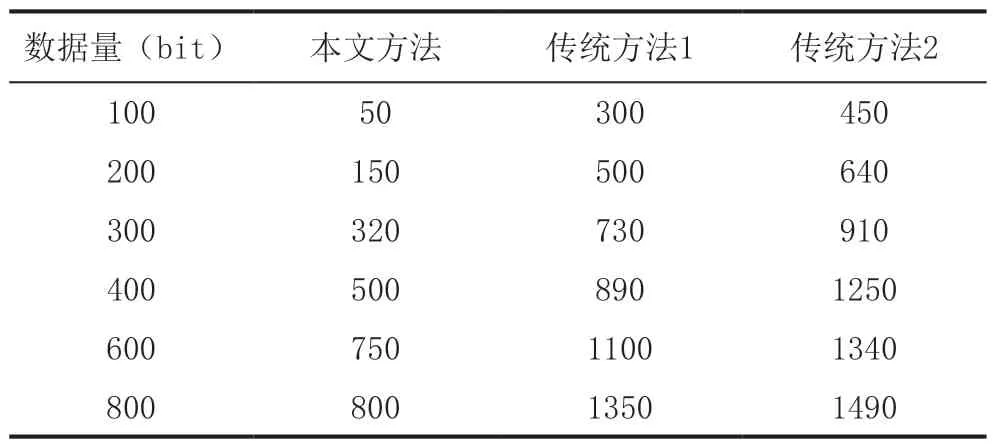
表2 混合数据近邻查询中数据量对I/O代价的影响

从表2 所示的实验结果可以看出，在混合数据近邻查询中数据量不变的前提下，应用本文设计的近邻查询方法进行混合数据近邻查询，数据量对I/O 代价的影响最小，而使用传统方法进行混合数据近邻查询，数据量对I/O 代价的影响较大。

综合实验结果，得到如下结论：相比传统方法，本文设计的空间数据库中混合数据的近邻查询方法在实际应用中效果良好，可以缩短查询过程中的CPU 运行时间，并降低数据量对I/O 代价的影响，提高地理信息系统近邻查询工作的可靠性。

6 结束语

经市场调研发现，空间数据库在信息决策系统、道路交通系统、地理信息系统中应用广泛，可将此类数据库作为开发地理信息系统的核心。在构建数据库时发现，空间数据库不仅具备传统数据库使用中的所有功能，还具备对空间信息与数据的描述、管理、检索、存储等功能。为发挥空间数据库在测绘地理信息生产领域的应用价值，提高对数据库中混合数据的利用率，本文以某地理信息系统为例，通过构建空间数据库混合数据Voronoi图、数据精简处理、混合数据KNN 查询，设计一种空间数据库中混合数据的近邻查询方法。为测试该方法的应用效果，引进两种传统方法作为参照，设计了对比实验，结果证明本文设计的方法可缩短查询过程中的CPU 运行时间，降低数据量对I/O 代价的影响。为进一步实现对本文方法近邻查询效果的优化，在现有工作基础上，加大对实验的投入，深化本文方法的综合性能，为地理信息系统在更多领域推广应用提供技术指导。