基于局部特征的图像匹配算法研究
罗 伟
(山东外贸职业学院,山东 青岛 266100)
0 引言
图像匹配技术在军事、工业和交通运输等众多领域有着重要的应用。近几年,计算机视觉和人工智能等新兴的人机交互技术得到了快速的发展,而图像匹配是实现人机交互过程的基础[1]。当前,我国在无人航拍领域中应用图像匹配主要是在构建、基本特征、特征编码以及内点筛选等几个方面进行研究。张震等[2]对无人机航拍中应用图像匹配的提取特征点进行分析,即将SIFT算法应用于其中,结果显示该算法具有较好的尺度以及旋转效果,但存在一定的耗费时间较长的不足。赵一粟[3]将加速鲁棒性算法应用于图像匹配,结果显示SURF算法描述符只有64个维数,但与SIFT算法相比,采用小波算法进行特征提取具有更高的效率。综上分析可以看出,当前国内学者针对图像匹配算法在无人机航拍领域中的研究已有一定的成效,但仍旧存在一定的匹配效率不高等问题。基于此,本研究将在前者研究的基础上提出一种新的算法模式,构建二进制鲁棒描述符(Binary Robust Independent Elementary Features,BRIEF),在此基础上应用该算法进行匹配,其匹配流程如图1所示。

图1 匹配流程
1 非线性ORB算法
1.1 非线性尺度空间构建
现有的SIFT、ORB等算法都是通过对高斯核的光滑处理来构建高斯尺度空间,虽然其计算效率很高,但是会导致图像的边缘、角点等信息损失的情况发生。本研究在此基础上提出利用各向异性非线性滤波器来构造标度空间,以获得稳定的标度空间。非线性扩散滤波器通过将不同尺度上的像质L的变化转换成一个由热扩散函数的散度因子所决定的扩散过程,其方程表达式如下。
(1)
在公式(1)中,L为图像亮度的矩阵;div与▽为热扩散函数的扩散度和图像梯度;c(x,y,t)则是传导函数,其表达式如(2)所示。
c(x,y,t)=g(|▽Lσ(x,y,t)|)
(2)
公式(2)中,t为尺度参数,▽L为图像L高斯滤波之后的梯度图像。
在此基础上分析非线性函数的表达式,可以直接借助AKAZE算法模式对其进行重新扩散,具体的表达式如下:
(3)
公式(3)中I为单位矩阵;A(Li)为图像Li的传导矩阵;n为显性扩散步数;Tj为恒定步长。
本研究选择的算法方式与SIFT算法有一定的相似,对应层组的表达式如下:
(4)
公式(4)中,σ0为初始尺度阐述,0×S为尺度空间总层数。非线性尺度空间的尺度因子σ可直接应用于对应的计算,其表达式如下:
(5)
1.2 算法特征的检测
已有的ORB方法中特征点的检测与描述子的构造都是在高斯标度空间完成的,但高斯滤波器的边界保护能力很弱。因此,本研究拟在非线性标度空间完成特征点的检测与描述子的构造。在上一部分建立一个非线性标度空间,然后在此基础上选取一个3个像素半径内的16个像素点,并将其作为参照点,再将其与其他16个素点进行对比。如果圆的中心与圆上的第1个和第9个像素有差异,内插值的绝对值大于16个像素与圆的中心点之间的差异,且到9的差异的绝对值大于阈值,那么圆的中心点就是特征点。
1.3 描述符的提取
在描述非线性尺度空间的特征点之后需要对其特征点的构建方式进行分析。本研究基于传统的ORB算法的基础上构建出一种新的方式,其表达步骤如下。
第一步,综合计算特征的矩阵获得计算方式:
(6)
第二步,矩阵的质心表达式为:
(7)
第三步,中心点到质心的表达式为:
(8)
在步骤(3)的基础上构建一个新的描述符的采样点,其表达式为:
(9)
在非线性尺度空间的基础上对其特征点进行描述之后,可以直接利用汉明距离的计算方式对其特征进行描述。
2 网格运动统计算法
通过以上几步实现了对航拍影像的初步匹配,但是由于影像中有很多错配点,需要通过特征点筛选算法来确定合适的配对点。在以往的研究中内点的筛选主要是利用随机抽样的相容性来进行,但是这种方法需要进行多个迭代式的运算,不仅运算量大,而且会影响到匹配的效率[4]。因此,本研究首先利用汉明距离进行初步的匹配,并利用广义最小二乘法对假配对点进行筛选。该方法的核心思路是:由于运动的平滑特性使得匹配点附近存在大量的对应点,从而可以根据对应点附近对应点的个数来判定匹配点的正确性。
将两张不同的图像进行匹配点的集合,其表达式如下:
Xi,L-R={x1,x2,...,xn}
(10)
公式(10)中,x1=(mi,mn),m和n分别表示匹配之后图像的任意匹配数量;任意匹配点的领域支持度Si=∣xi∣-1。这些匹配点能够同时满足不同面积之间相互分布的点,其表达式如下:
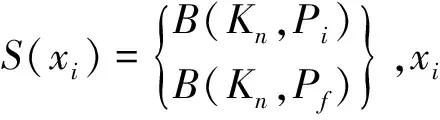
(11)
由公式(11)演变的网格统计算法的表达函数为:
(12)
公式(12)中,得出的数值越大,则表明最终的计算准确值越高。
3 实验论证
通过ORB、ORB+GMS、AKAZE、AKAZE法、GMS等算法与SUIRD数据集进行比较,验证本项目提出的非线性ORB+GMS算法在航空影像匹配方面的优势。SUIRD数据集一共有4个组别,它们具有不同的变化图像,分别是水平旋转、竖直旋转、尺度变换和混合变化。每一个组别中都有6张图像,且变化程度逐渐增加。第一个组别为参考图像,其他5个组别为待匹配图像。将待匹配图像放置于Ubuntn18.04系统中进行操作实验。
3.1 匹配算法的准确度
为增强ORB的稳健性,研究通过对特征点的检测与特征值的提取,使ORB的稳定性大大提高;使用AKAZE方法构造的LDB描述子不但对象元进行了编码,而且加入了梯度信息,因此其鲁棒性比传统的非线性ORB方法要好。在航空影像中,当影像含有混合变异时,使用ORB方法得到的匹配精度是最小的;文中提出的非线性ORB方法的匹配准确率低于AKAZE方法,但是要高于ORB方法。用GSM方法对内点进行筛选,ORB方法的精确度达到了0.912,但是与非线性ORB+GMS、AKAZE+GMS相比还是有一定的差距。与传统的ORB+GMS方法相比,该方法的匹配精度分别为0.950和0.04,与传统的AKAZE方法相比该方法的匹配精度分别为0.043和0.04;与传统的ORB+GMS方法相比,该方法的精确度提高了0.041;与传统的ORB+GMS方法相比,非线性ORB+GMS方法的匹配精度提高了0.041。在垂直方向上与 AKAZE方法相比本研究提出的非线性ORB方法的匹配精度下降了0.06,而ORB方法的匹配精度提升了0.056。与AKAZE+GMS算法相比,非线性ORB+GMS算法的匹配准确率降低了0.01,与ORB+GMS算法的匹配准确率提高了0.05,如图2—5所示。
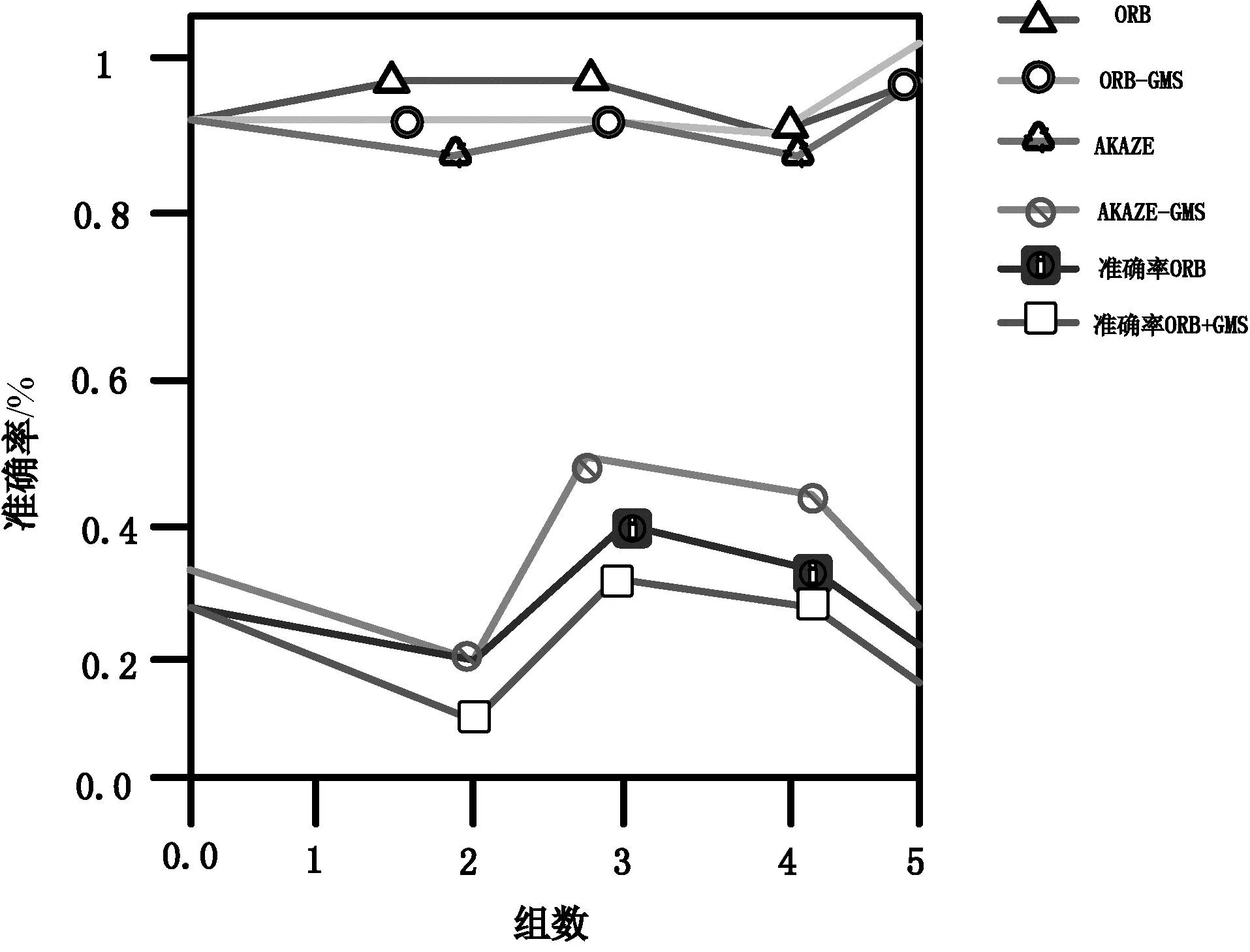
图2 混合变化准确率
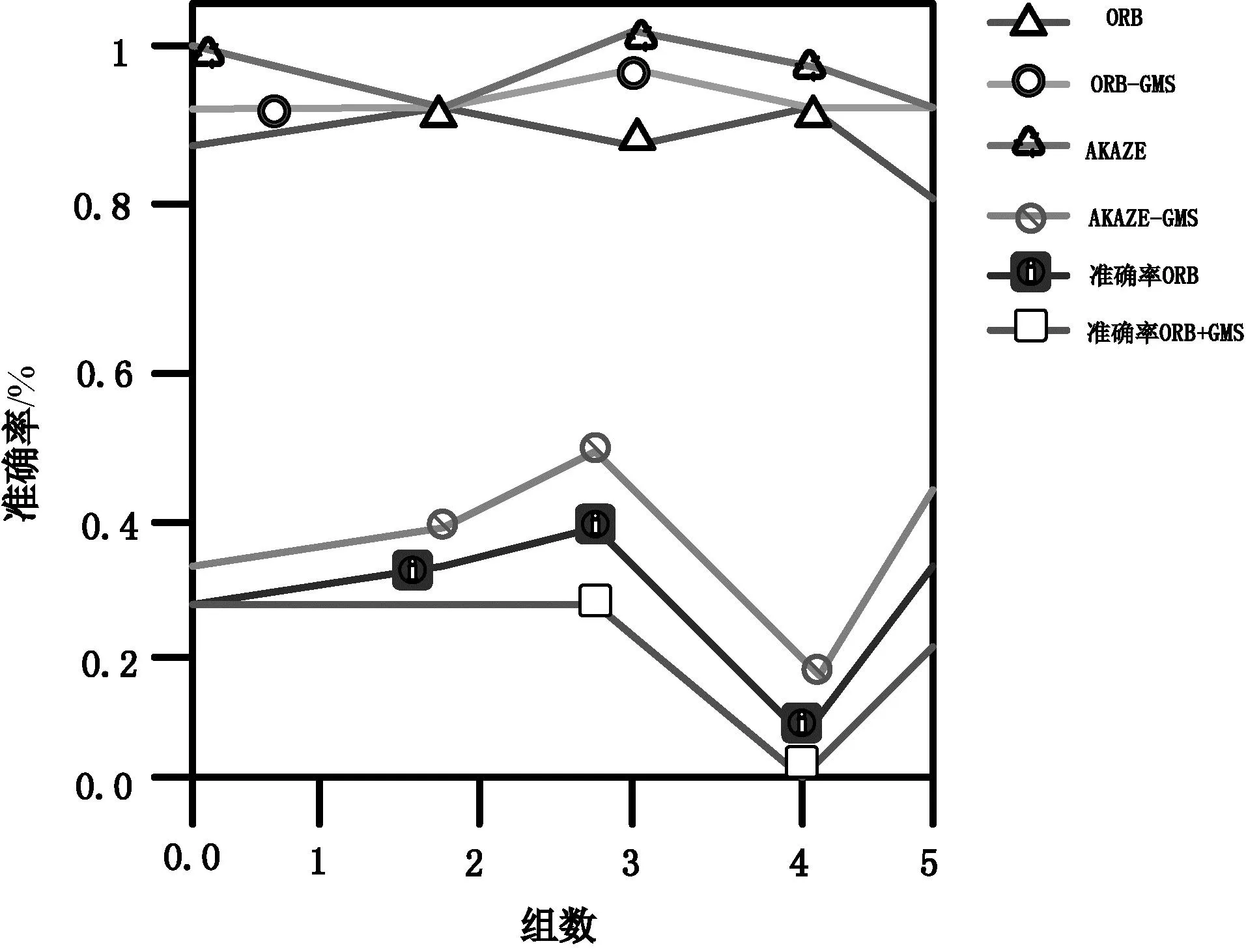
图3 水平旋转变化准确率

图4 尺度变化准确率
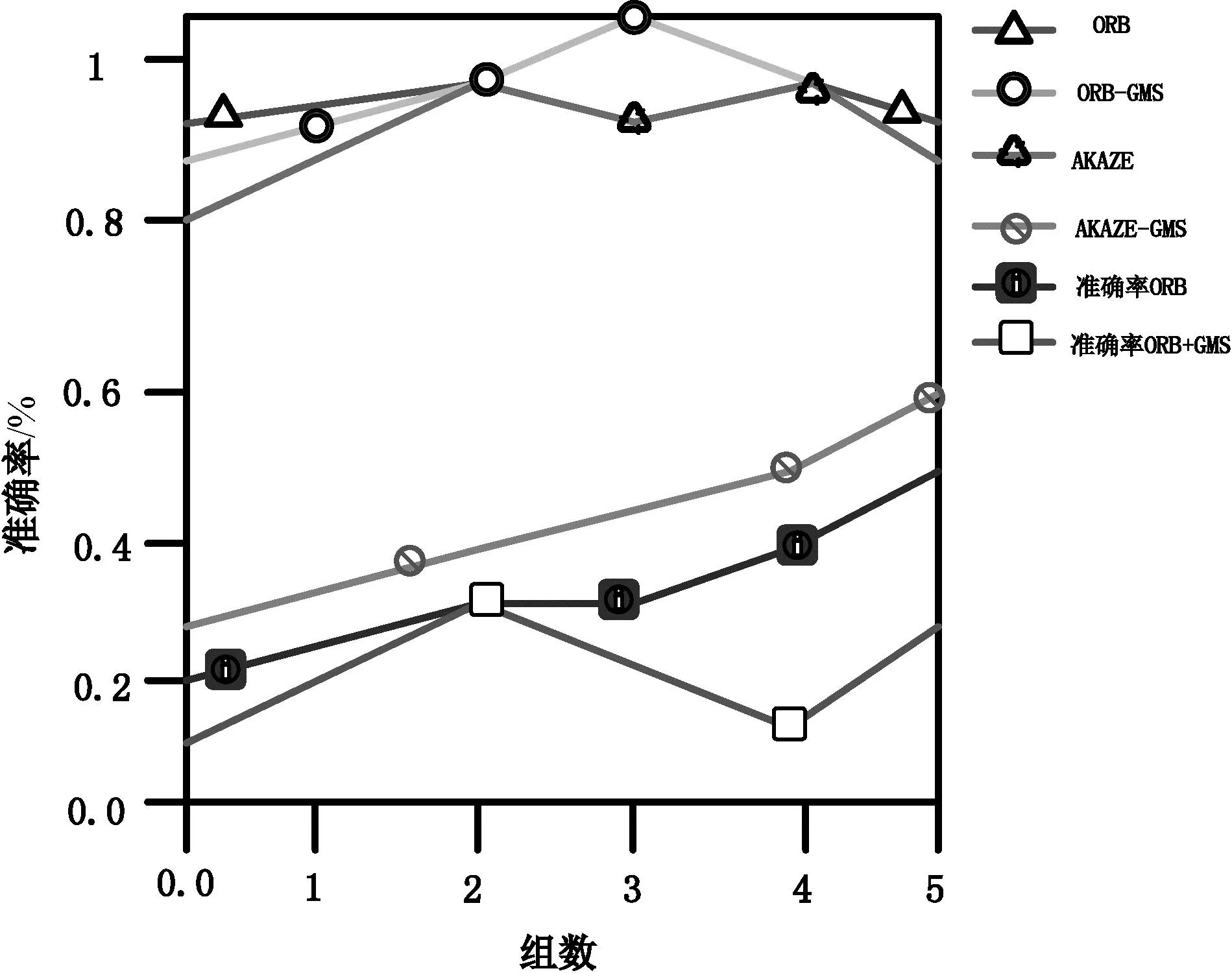
图5 竖直旋转变化准确率
3.2 匹配效率分析
对ORB算法、ORB+GMS算法、AKAZE算法 AKAZE+GMS算法和本文所提算法在混合变化图像组匹配耗时进行统计,具体结果如表1所示。ORB方法在高斯函数的帮助下可以迅速地建立比例尺空间,同时也可以快速地建立特征点的提取和描述子的构造,从而使得ORB方法的时间最短,匹配效率最高;但是,从曲线图2可以看出ORB算法具有最小的匹配准确率和最小的稳定性。其中,非线性ORB方法是利用非线性过滤函数构造标度空间,但由于需要对其进行迭代求解的计算时间比较长,所以其匹配效率比ORB方法低;与ORB方法相比,非线性ORB方法的匹配准确率更高,且稳定性更好。由于AKAZE算法在构造描述子时既要求解一个非线性的函数,又要计算一个图像的斜率,所以其匹配的效率不如一个非线性的ORB算法;从图2可知与非线性ORB方法与AKAZE方法相比匹配准确率更高,但是与非线性ORB方法相比,AKAZE方法的匹配时间更长。

表1 不同算法的耗时统计 单位:min
4 结语
本研究针对ORB算法中的尺度空间构造方式容易导致影像中存在的角点、边缘等信息缺失,导致影像匹配精度不高的问题,研究一种基于非线性尺度空间的ORB算法,并在此基础上提出了一种新的方法,该方法利用一种新图像匹配算法构造一种新的非线性标度空间。采用BRIE快速算法进行特征点的提取;利用GMS算法对内点进行筛选。试验结果表明:该方法稳定、高效,在航空影像匹配中有很好的适用性。

