面向微细加工的二自由度磁悬浮平台

魏发南，刘 英

（福州大学先进制造学院，福建 晋江 362200）

微细加工技术是一种制造微小尺寸零件的加工技术，其加工平台具有毫米级别的行程和微米级别及以下的定位精度[1].激光微细加工以无机械冲力、加工对象局限性小的特点而被广泛研究.为提升工件的加工精度，研究更多集中在如何减少加工表面热损伤.文献[2-4]采用高频的脉冲激光（如纳秒激光、飞秒激光、皮秒激光）实现高精度加工，激光的脉冲频率越高，则越能对材料实现几乎无热效应的加工.文献[5]采用水辅助激光加工技术，通过水层带走加工过程中的热量和碎屑来缩小热影响区.然而，除却表面热效应的影响，移动台的定位精度也与工件的加工精度有直接影响.激光微细加工移动台通常采用步进电机进行驱动，在传动过程中不可避免存在机械摩擦，影响定位精度.磁悬浮作为一种磁力克服重力的技术，因其无接触的特性很好地避免了部件之间的直接接触与摩擦损耗，在交通运输、轴承、高精密数控机床等领域得到广泛的研究[6-10].将磁悬浮的无接触摩擦特性运用于激光微细加工移动台，为进一步提升加工精度提供了可能性.

在磁悬浮定位平台的研究中，文献[11]提出一种二维磁悬浮定位平台，由6 对电磁铁实现悬浮支撑与平面运动.文献[12]采用电磁铁实现悬浮控制、直线电机进行驱动的方式，构建多自由度的磁悬浮平台.文献[13-14]考虑多个线圈组合排列，共同驱动永磁体载体实现六自由度的运动.以上研究中，因电磁铁或线圈阵列均承载着平台悬浮的功能，平台面临着能耗与温升问题.永磁体因其低能耗的固有属性而被广泛研究.文献[15]提出一种完全永磁悬浮装置，通过改变盘状永磁体的旋转角度调整磁通量，从而改变悬浮力大小，可实现零功率悬浮控制.文献[16]提出间隔分布的方形永磁体作为定子，驱动器为线圈阵列的永磁平面电机.文献[17]提出由4 组线性哈尔巴赫阵列作为定子以及对应的二相线圈绕组为驱动器的磁悬浮平台.在上述磁悬浮平台中，永磁体阵列或者哈尔巴赫阵列替代电磁铁或者电磁线圈提供悬浮力，有效避免悬浮控制所需的能耗.但由于永磁体阵列或者哈尔巴赫阵列既提供悬浮力，也提供驱动力，不可避免地存在耦合的问题.解耦问题往往是磁悬浮系统性能优化的关键，也是重难点问题，因此，研究人员在模型优化和控制算法上进行了许多尝试与探索[17-22].

本文提出一种新型磁悬浮平台运用于激光微细加工装置中.在该平台中，永磁斥力抵消重力，从而可忽略垂直方向的运动控制，电磁线圈用来实现水平方向的驱动.由此，不仅可以避免悬浮力与水平驱动力的耦合，也消除了因电磁力平衡重力而产生的功耗和热量.同时针对该磁悬浮平台，采用分散控制策略，设计对动态响应过程具有一定鲁棒性的模糊PD（proportional-derivative）控制器，结果表明，该磁悬浮平台具备毫米级的平面运动行程以及微米级的定位精度.本文安排如下：首先，介绍磁悬浮定位平台的结构及其工作原理；其次，基于文献[23]进行平台的数学建模并建立动力学方程，以此进行控制器的设计，考虑平台多点悬浮支撑的结构特性，采用分散控制[24]降低控制器的设计难度，同时设计可实时修正PD 参数的模糊PD 控制器；最后，搭建实验平台进行实验验证.

1 磁悬浮定位平台

1.1 系统结构与工作原理

磁悬浮定位平台三维模型结构如图1 所示，由3 组定子基座、3 个圆柱永磁体、载物平台构成.定子基座包括线圈阵列、线性霍尔传感器、环形永磁体.定子基座中的线圈阵列（共4 个）位于环形永磁体上方，线圈绕圆环永磁体的中心轴线阵列分布，两两组合提供沿着x、y方向的水平电磁力.线性霍尔传感器位于线圈阵列的中心轴线处，高度位于线圈高度的一半处，用于测量圆柱永磁体沿x、y方向移动时的磁场变化.定子基座之间相互间隔120° 呈圆周分布，定子基座的中心距原点的距离为100 mm.最下方的圆形底座的半径尺寸设计为170 mm，便于固定3 个环形永磁体.圆柱永磁体固定在载物平台上，与载物平台共同构成移动台.将一组定子基座和圆柱永磁体定义为一组子单元，3 组子单元具有一致的物理参数.每组子单元中，圆环永磁体剩磁0.23 T，内、外径分别为60、100 mm，高度15 mm；圆柱永磁体2 个，剩磁1.03 T，直径40 mm，高度5 mm；线圈内、外径分别为7、25 mm，电感4.28 mH，电感5.5 Ω.

图1 磁悬浮平台三维模型Fig.1 Three-dimensional model of maglev platform

本文的磁悬浮平台中两两线圈组合提供一组电磁力，共提供6 组电磁力.现通过有限元仿真方式[23]对其中一组圆柱永磁体与线圈间的相互作用力进行分析，建立图2 所示坐标系.电磁力的磁力大小与线圈电流成比例关系，取线圈电流为1 A，作归一化处理.图2 为圆柱永磁体在固定高度下，沿x方向移动一定距离后再往y方向偏移0、1、2、3 mm 时圆柱永磁体所受电磁力大小.图2（a）表明，在x≤ 3 mm，y≤3 mm，圆柱永磁体往y方向偏移时，电磁力在x方向的分量变化微小，最大变化量发生在x=0，y=3 mm处，其值为0.010 N，变化幅度为1.5%；电磁力在y方向的分量随着偏移距离越远，其值增加，最大仅为0.008 N，为x方向电磁力分量的1.4%.图2（b）表明，在x≤ 3 mm，y≤ 3 mm，圆柱永磁体往y方向偏移时，电磁力在z方向的分量变化微小，最大变化量发生在x=2 mm，y=3 mm 处，其值为0.010 N，变化幅度为0.7%.由此可认为，由两两线圈组成的结构中，在固定高度以及3 mm×3 mm 平面范围内，电磁力的大小与在y方向的位置无关，仅与在x方向的位置以及电流大小相关；假设电磁力在y方向的微小分量为外部扰动.由此线圈仅产生沿两线圈中心连线方向的电磁力分量以及竖直向上的分量.

图2 不同偏移距离下电磁力在x、y、z 方向的分量Fig.2 Components of electromagnetic force in x,y,and z directions at different offset distances

对平台能否实现一定平面范围内稳定的悬浮高度，进行了以下探究.在重力与永磁斥力平衡的高度处，动子沿平面内移动，令竖直方向上所受电磁力与永磁斥力之和的变化量与动子的重力之比为k.若k＜0.1，且在该水平范围内，悬浮高度变化微小，即可认为在此水平范围内动子在竖直方向上合力为0，可忽略垂直方向上的控制[23].对本文所述的子单元结构进行分析，图3 为圆柱永磁体沿x、y方向移动，电磁力与永磁斥力之和在竖直方向上分量的变化情况以及对应k值变化.由图3 可知，本文所述的结构在 ±2 mm 内，k值始终在10%以内，永磁斥力与电磁力在竖直方向上变化量最大为0.017 N，悬浮高度变化不到0.2 mm，因此，可认为平台结构在4 mm ×4 mm 的平面范围内只需考虑x、y方向的运动控制，而忽略垂直方向上的控制.

图3 竖直方向上的电磁力与永磁斥力之和以及k 值Fig.3 Sum of electromagnetic force and permanent magnet repulsion in vertical direction and k value

磁悬浮平台的3 组子单元中环形永磁体对移动台产生一致的、竖直向上的排斥力，排斥力之和用于抵消移动台部分重力.子单元中同一轴线方向的两个线圈反向串联产生一组电磁力，3 组子单元的水平方向的电磁力总和与环形永磁体产生的被动偏移力共同驱动移动台在平面内移动.

2 系统动力学模型

图4 为磁悬浮平台的受力分析简图，原点O设在载物平台的质心位置处，建立全局坐标系，并确定3 组子单元的序号，按逆时针排序为1、2、3.令圆环永磁体对圆柱永磁体的作用力为Fm，两两组合的线圈对圆柱永磁体作用力为Fe，圆柱永磁体与载物平台的质量之和为m.将圆柱永磁体统称为动子.将Fm在x、y、z方向上分别分解为Fmx、Fmy、Fmz.令i=1,2,3，依次表示3 个子单元，则第i组子单元在x、y、z方向上的永磁斥力为Fmxi、Fmyi、Fmzi，对应电磁力为Fexi、Feyi、Fezi.平面内系统的动力学方程为

图4 磁悬浮平台的受力分析Fig.4 Force analysis of maglev platform

式中：θ 为磁悬浮平台绕z轴旋转的角度；J为转动惯量；fx、fy分别为x、y方向上的外界干扰力；φi为单元i动子质心和原点的连线与x轴正方向按顺时针所形成的夹角；L=100 mm，为各子单元中动子的质心到全局坐标系原点的水平距离；M为外界干扰力矩.

本文的磁悬浮实物平台设计中各个子单元具有一致的几何参数和几乎一致的磁场特性，可认为各个子单元具有一致的数学模型.以其中一个单元中圆柱永磁体在x方向为例，通过COMSOL Multiphysics®得到永磁体和电磁线圈的有限元仿真模型，通过多项式拟合获得磁力公式，由此得到的偏移力Fmx1和电磁力Fex1分别为

同理，在y方向的偏移力Fmy1和电磁力Fey1分别为

式（4）～（7）中：kmi为单元i中动子的被动偏移力刚度系数，kei为单元i中动子的电磁力刚度系数，kIi为单元i中动子的电流刚度系数，I1、I2分别为单元1在x、y方向线圈所通的电流.

通过多项式拟合，偏移力和电磁力的各项系数以及拟合程度如表1 所示，其中，偏移力和电磁力的拟合度分别为0.998 7、0.994 1.

表1 拟合后的各项系数Tab.1 Various coefficients after fitting

因本文仅探究平面内的平移运动，暂未考虑平台绕z轴旋转的问题.将式（4）～（7）代入式（1）、（2）中，得到系统的动力学方程为

式中：I3、I4分别为单元2 在x、y方向的线圈所通的电流，I5、I6分别为单元3 在x、y方向的线圈所通的电流.

在结构设计中，放置6 个霍尔传感器检测3 个单元分别在x、y方向的运动，所测量的位移变化量(x1,y1)、(x2,y2)、(x3,y3)分别为

3 控制器设计

由于磁悬浮系统具有开环非线性的特点，需要设计反馈控制以达到稳定的状态.分散控制可忽略各个单元之间的耦合关系，独立控制各个单元，使得控制器具有设计简单、易于实现的优点，该策略在工程实际中运用广泛[24-25].模糊PID 控制运用模糊语言与专家知识，可在线对PID 参数进行适应性调整，具有一定柔性，在动态响应过程中具有良好的鲁棒性.磁悬浮平台基于多点支撑悬浮驱动的结构特性，采取分散控制策略，且磁悬浮平台系统为滞后系统，因此，选用具有超前补偿的PD 控制算法与模糊控制相结合，实现平台运动过程中的稳定调节.本文基于分散控制策略对3 组子单元的x、y方向均采取独立的模糊PD 控制算法.因本文仅探究了平面内的平移运动，3 组子单元给予相同的参考信号实现平台整体移动，因此，3 组子单元具有一致的调节过程.下面以单元1 为例进行模糊PD 控制器的设计以及描述其控制过程.

3.1 模糊PD 控制器设计

以单元1 中的x方向为例，PD 控制器的传递函数G(s) 为

式中：E(s) 为输入控制器中的偏差量，U(s)为控制器的输出量，P为比例系数，D为微分系数，s为复频率.

模糊控制流程如图5 所示.将动子位移的偏差量E与偏差变化量Ec为模糊控制器的2 个输入，选用三角隶属度函数对输入量和输出量进行模糊化处理，模糊量的子集选用 {NB（负大），NM（负中），NS（负小），ZO（零），PS（正小），PM（正中），PB（正大）}，根据由实践经验和专家知识组成的知识库进行模糊规则推理，输出模糊量，采用重心法对输出量进行解模糊处理，输出参数P、D经模糊控制器输出的变化量 ΔKp、ΔKd，如式（11）、（12）所示.

图5 模糊控制器流程Fig.5 Flow chart of fuzzy controller

由于浮子位置变化范围为4 mm，令E的基本论域为 [-2，2]；在数字控制器中，Ec表现为当前偏差与上一次偏差的差值，令Ec的基本论域为 [-1，1]；依据PD 控制环节的调试经验，设定 ΔKp和ΔKd的基本论域分别为[-0.01，0.01]、[-0.1，0.1]；同时，结合前人经验以及实际控制经验确定模糊规则表.模糊控制器的量化因子、变量的基本论域、模糊论域、ΔKp和 ΔKd的模糊规则，见表2～4.

表2 模糊控制器参数Tab.2 Parameters of fuzzy controller

表3 Δ Kp 的模糊规则Tab.3 Fuzzy rule ofΔKp

表4 ΔKd的模糊规则Tab.4 Fuzzy rule of ΔKd

本文由数字控制器实现3 组子单元的模数转换、模糊PD 算法计算以及驱动电压控制.单元1 系统控制过程如下：单元1 中线性霍尔传感器检测到由动子位移变化带来的磁场信号变化，将其转化成电压信号，通过信号放大电路传输至控制单元的模数转换模块（AD 变换），得到信号值，与参考信号作比较后输入控制单元，控制单元实时计算并输出PWM（pulse width modulation），经光耦隔离后传输至驱动电路，并输出相应的电压，电压信号传输至线圈两端转换成电流信号，由此线圈产生电磁力，与圆环永磁体产生的偏移力共同调整子单元中动子在水平面内的移动.单元2、3 系统控制过程同上.单元1系统控制过程如图6，图中：U1为位移量x1经传感器输出的电压信号.

图6 单元1 的x 方向控制框图Fig.6 Control block diagram of unit 1 in x direction

4 实 验

磁悬浮平台整体架构如图7 所示，基于CortexTMM4 内核的高性能微控制器STM32F407ZGT6 是控制系统的核心，接收由3 个子单元的线性霍尔传感器SS495A 输出的电压信号，同时独立输出各单元的电压控制信号.其中，线性霍尔传感器的分辨率为3.125 mV/Gs，微控制器输出位移信号的分辨率为2.85 μm.上位机实时监测平台的位移信号，示波器提供可视化的线圈电压波动信号.

图7 磁悬浮平台的整体架构Fig.7 Overall structure of maglev platform

本文仅探究磁悬浮平台在平面内的平移运动，所以在实验中给予3 组子单元一致的位移参考信号.采用3 组子单元测量的位移量平均值表示平台整体的位移.引入均方根误差eRMSE（式（14））和最大跟踪误差量化磁悬浮平台的控制效果.

式中：ej为第j个采样点的实际测量值与参考值的偏差；N为采样点的数量.

4.1 控制器比较

对磁悬浮系统分别采取PD 控制和模糊PD 控制，并进行x方向上0.5 mm 的阶跃响应以及幅值为0.5 mm 的余弦跟随实验.在PD 控制实验环节，对P、D参数进行多次调整，最后取3.0，以获得较小的均方根误差和稳定的动态跟随曲线.令PD 控制最终P、D参数与模糊PD 控制中初始P、D参数取值一致.图8 为磁悬浮平台在x方向上的阶跃响应，其步长为0.5 mm.由图可知：PD 控制阶跃响应具有明显的超调现象，其超调量达到0.411 7 mm；而模糊PD 控制阶跃响应的超调量仅为0.093 1 mm，为前者的22.6%.

图8 x 方向上的0.5 mm 阶跃响应曲线Fig.8 Step response curve of 0.5 mm in x direction

图9 为磁悬浮平台在x方向上2 个周期的余弦跟随曲线，幅值为0.5 mm.由图可知：模糊PD 控制相较于PD 控制具有更好的动态性能；PD 控制下的跟随曲线均方根误差为0.075 1 mm，最大跟踪误差为0.403 2 mm；而模糊PD 控制下的跟随曲线均方根误差为0.046 9 mm，最大跟踪误差仅为0.156 8 mm，是PD 控制下的38.8%.综上可知，在相同的初始参数下，相较于PD 控制算法采用模糊PD 控制算法，能够有效降低超调量，并且具有更优的动态调节性能.

图9 x 方向上的余弦跟随曲线Fig.9 Sinusoidal following curve in x direction

4.2 悬浮实验

在微控制器中给定3 组子单元一致的参考位置（x1,x2,x3,y1,y2,y3=0），随后给系统上电，将平台放置在定子基座上方，直至平台实现悬浮.图10 为放置平台至稳定悬浮的过程.

图10 磁悬浮平台在x、y 方向的静态悬浮过程Fig.10 Static levitation process of maglev platform in x and y directions

图10 表明：在5 s 后平台趋于稳定，并能够维持长时间的稳定状态；平台在静态悬浮状态下，x、y方向的均方根误差分别为7.19、2.95 μm，其最大跟踪误差分别为17、11 μm.由此可认为，该磁悬浮平台具有良好的悬浮效果，能够实现微米级的悬浮精度.

4.3 步进响应实验

为验证该磁悬浮平台可实现大范围的行程，对磁悬浮平台进行0.028 5 mm 的小步长位移响应，如图11 所示.

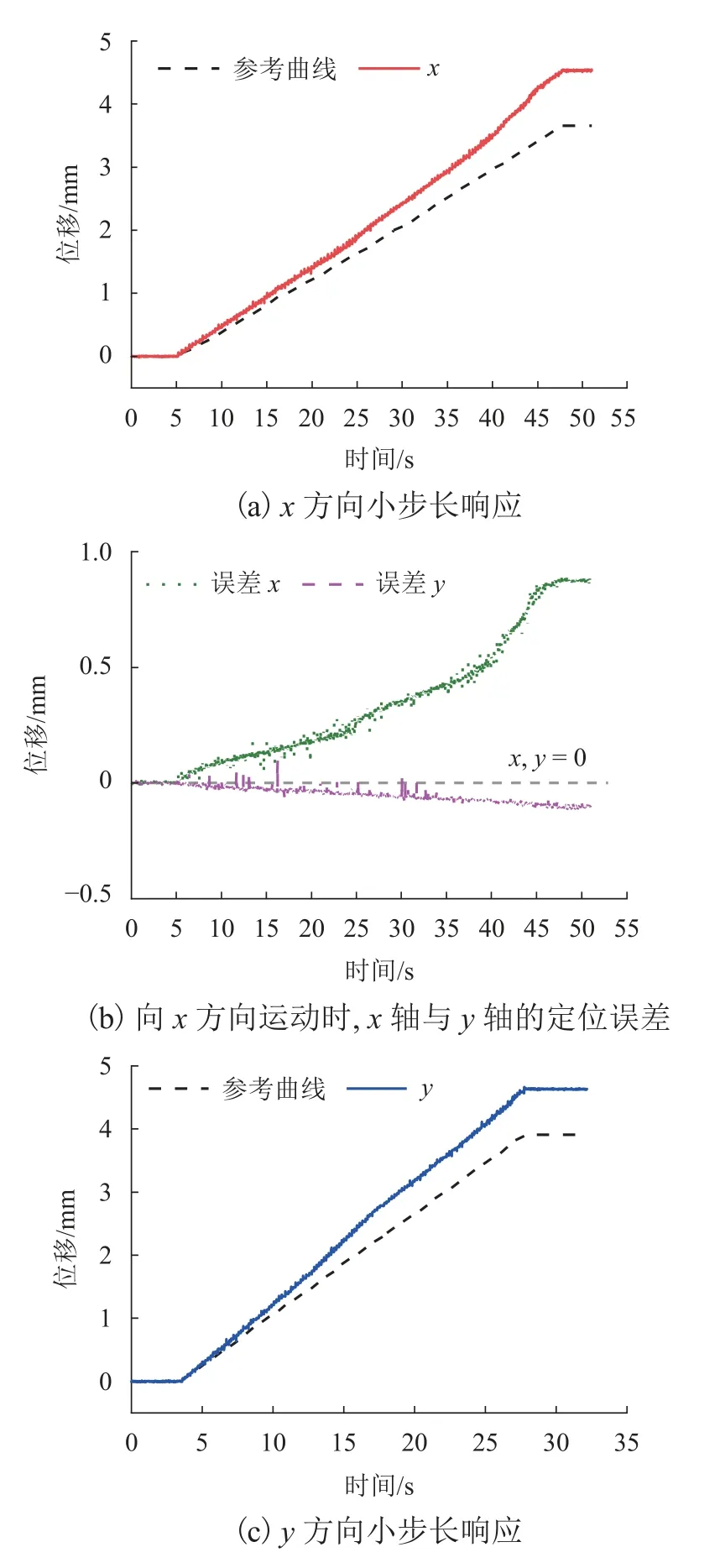
图11 平台小步长响应曲线Fig.11 Small step response curves of platform

图11 表明：x、y方向小步长响应均能够稳定地跟随参考曲线，且行程范围分别为4.5 mm 和4.6 mm；随着x方向的步进响应，y方向的最大跟踪误差不超过0.16 mm；随着y方向的步进响应，x方向的最大跟踪误差也不超过0.16 mm，由此可认为，该磁悬浮平台具备x与y方向解耦的能力.但不可避免的是，随着参考位移的增加，实验跟随曲线的均方根误差也在不断增加.x方向的均方根误差由0.004 9 mm 增加到0.874 8 mm，y方向的均方根误差由0.006 1 mm 增加到0.721 0 mm，其原因在于控制环节缺少积分项而造成稳态误差不断累积.

4.4 双轴组合工作实验

为验证磁悬浮平台具有x与y轴的组合工作能力，对磁悬浮平台进行直径为1 mm 圆形轨迹的运动响应，如图12 所示.图中：红色圆点表示为直径为1 mm 的圆形参考曲线，其中步进角度为60/π；蓝色方框表示平台的实验跟随曲线.图13 为实验跟随过程中，实测值与参考值的误差散点图.实验数据表明：圆形跟随轨迹的均方根误差为0.095 4 mm，最大跟踪误差为0.244 8 mm.因此，从实验曲线上来看能够实现很好地跟随，磁悬浮平台具有一定的组合工作能力.

图12 平台进行直径1 mm 的圆周运动Fig.12 Circular motion of platform within diameter of 1 mm

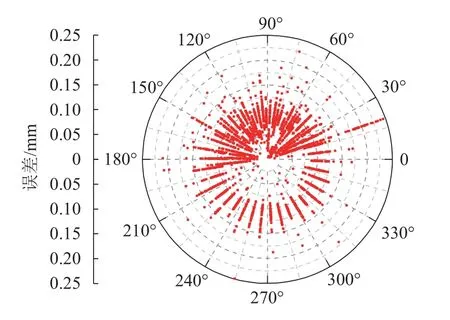
图13 实测值与参考值的误差分布Fig.13 Error distribution of measured and reference values

5 结论

本文介绍了所设计磁悬浮平台的结构和工作原理，并建立平面内的系统动力学方程，进行模糊PD 控制器设计，最后设计实验验证平台的静态悬浮能力以及平面内运动控制能力，得出以下结论：

1）针对激光微细加工的移动平台存在机械摩擦问题，提出一种新型的二自由度混合斥力式磁悬浮平台.在 ±2 mm 内，该平台所受垂直方向的合力变化为0.017 N，悬浮高度变化在0.2 mm 内，因此，可近似认为该平台垂直方向合力为0，可忽略垂直方向的运动控制，从而实现悬浮与驱动解耦.

2）基于平台的多点悬浮驱动控制特性，采用分散控制策略，设计模糊PD 控制器.通过实验对比可知，与PD 控制器相比，本文提出的模糊PD 控制器能够有效减少超调量，超调量为前者的22.6%，并且最大跟踪误差为前者的38.8%，具有更优的动态响应特性.

3）搭建实验平台进行试验，实验结果表明该磁悬浮平台具有良好的静态悬浮效果，x、y方向静态悬浮的均方根误差分别为7.19、2.95 μm.实验同样验证了该平台在x、y方向均可实现4 mm 的行程范围，且具备x、y轴的组合工作能力，即该平台可满足4 mm × 4 mm 的平面范围内的运动控制.

综上，本文提出的新型磁悬浮平台具备悬浮与驱动解耦的能力；同时所设计的模糊PD 控制器使得平台具有平面内运动可控的能力，能够实现毫米级的行程以及微米级的精度.为磁悬浮技术运用于激光微细加工，提高其加工精度提供了可能性.但实验数据同样表明，结果仍存在一定的稳态误差，同时各单元之间的耦合仍然不可忽略.因此，为提高运动控制的准确性，在后续的工作中将引入积分控制项或者采纳更为合适的控制算法，满足快速响应和稳定性的同时，进一步消除稳态误差.