分离式螺旋钻具截割与输送协同优化研究
张 强 ,刘 伟 ,张润鑫 ,李宝岐 ,顾颉颖
(1.山东科技大学 机械电子工程学院, 山东 青岛 266000;2.辽宁工程技术大学 机械工程学院, 辽宁 阜新 123000)
0 引 言
螺旋钻机作为矿山生产的重要设备,被广泛应用于井下瓦斯抽放、区域卸压、极薄煤层与露天矿端帮开采等领域[1-3]。随着煤矿智能化发展,提高煤机装备自动化水平与设备工作效率已成为大势所趋,降低煤机装备开采能耗已成为推进绿色矿山建设的必然要求。钻具作为钻机高效开采的关键结构,为提高钻具的截割与输送性能,降低钻具截割输送能耗,国内外众多学者进行了大量研究,文献[4]建立了钻具输送量和输送能耗数学模型,以提高输送量并降低输送能耗为目标,对钻具结构参数进行优化,并通过试验验证了优化结果的正确性;文献[5]以螺旋钻杆结构参数与转动速度为变量,以输煤生产率最大和能耗最低为目标,利用遗传算法和蚂蚁算法的混合算法对优化目标进行求解,有效提高了螺旋钻杆的输煤效率;文献[6]以钻杆重量最轻为优化目标,对螺旋钻杆进行结构参数优化,降低钻杆重量的同时提高了钻杆的强度;文献[7]设计了一种定心螺旋钻头,可实现对土壤进行二次切削,提高了钻头的切削性能;文献[8]将螺杆输送长度作为变量考虑到螺杆输送能耗模型中,以螺旋输送总能耗最小、输送效率最大化为目标,对螺杆的螺距、转速和输送长度进行优化,有效提高螺杆输送性能;文献[9]研究发现多钻头并行钻采时,钻头间的相互作用可以改善各钻头的截割性能,并指出钻具性能优化过程中,钻头和钻杆各自优化结果均会存在一个最优转速,钻具转速的优化结果存在一定的局限性。其主要原因在于截割钻头与螺旋叶片通过焊接的方式进行连接,两者在驱动电机下同步转动,钻具的结构特点给转速优化结果带来了局限性。为解决螺旋钻具截割转速与输送转速不匹配问题,提高钻具开采效率,降低钻具开采能耗,提出一种新型分离式螺旋钻具及其截割与输送过程协同控制策略,为螺旋钻机绿色开采提供参考。
1 分离式钻具结构设计思路
分离式钻具将截割钻头与螺旋钻杆进行分离,分别利用独立的控制系统对其转速进行控制。如图1 所示,分离式钻具是在传统钻具基础上的改进,通过增加内杆的方式将截割钻头与螺旋钻杆进行运动分离。内杆限制在螺旋钻杆内与杆轴线同轴转动,内杆一端与截割钻头连接,一端与截割电机连接,截割驱动力通过内杆传递到截割钻头,而该过程中螺旋钻杆不发生转动,螺旋钻杆的驱动力由单独的输送电动机进行控制,从而实现截割钻头与螺旋钻杆间的运动分离。
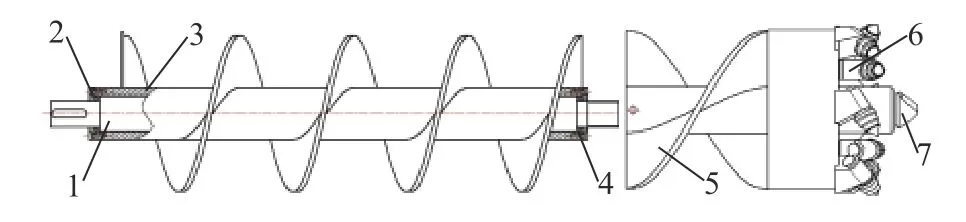
图1 分离式钻具结构设计示意Fig.1 Schematic design of separate drilling tool structure
多钻杆拼接时,相邻内杆间通过联轴器传递动力,相邻螺旋钻杆通过端盖间的配合传递动力,从而解决分离式钻具加装钻杆后动力传递连续性问题。如图2 所示,新型分离式钻具使用过程中的控制单元包括进给速度控制、截割转速控制与输送转速控制,钻具推进过程中,截割钻头与螺旋钻杆保持相同的进给速度。

图2 分离式钻具协同控制策略Fig.2 Separate drilling tool cooperative control strategy
对于螺旋钻机,钻具单位时间的开采体积与钻具的进给速度成正相关,钻具的单位时间的输送能力与螺旋钻杆的转速成正相关。而螺旋钻具的进给速度普遍较低[10-11],当截割钻头单位时间截割的煤岩体积低于螺旋钻杆单位时间的输送能力,将导致螺旋钻杆做一定的无效功造成能耗浪费;当截割钻头单位时间截割的煤岩体积高于螺旋钻杆单位时间的输送能力,将导致截割的煤岩不能及时输送出钻孔在螺旋钻杆内堆积,严重影响钻具的使用安全,寻求截割钻头与螺旋钻杆间的钻速合理分配,对减少钻具无效做功,降低钻具开采能耗有着重要影响。
2 钻具截割与输送能耗分析
2.1 钻头截割比能耗分析
分离式钻具依靠其结构的独特性,将钻头截割过程与钻杆输送过程由原来的整体同步分割为2 个相互独立的子系统,因此,钻具整体的开采能耗可分解成钻头截割能量消耗与钻杆输送能量消耗2部分。
由于截割钻头结构复杂很难通过准确的数理方程对煤岩截割过程进行定量描述,通过离散元数值模拟的方法对钻头截割能耗进行仿真分析。参考LC-QH-12 型露天矿螺旋采煤机钻具尺寸建立等比例钻头三维模型(图3),所建钻具直径1 200 mm,钻头叶片螺距1 000 mm。为研究煤岩硬度、截割转速、进给速度对钻头截割能耗的影响规律,通过EDEM 建立3 种不同硬度的模拟煤壁进行钻具截割模拟,所建煤壁的煤岩属性见表1[12]。
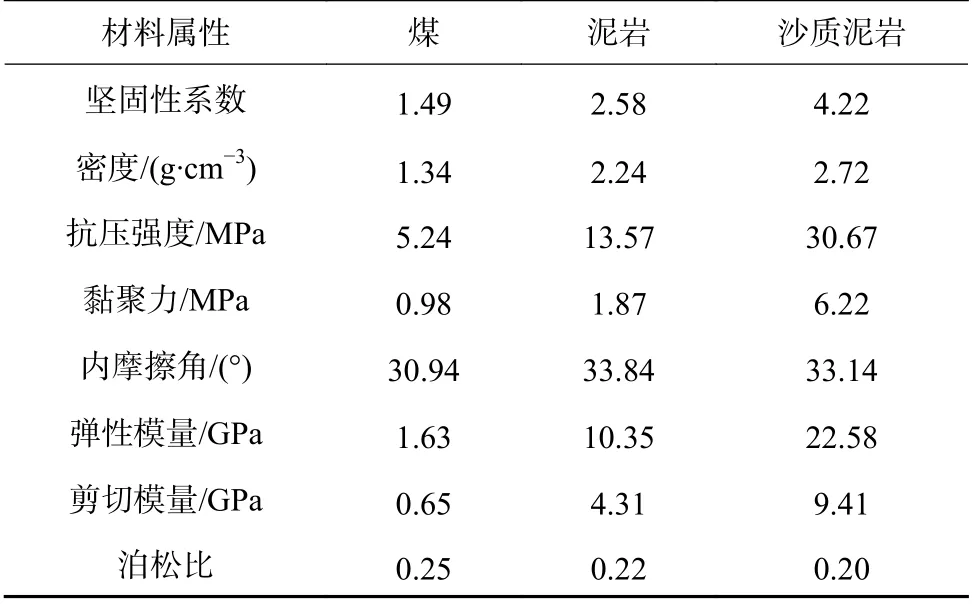
表1 煤岩力学参数Table 1 Coal rock property parameters

图3 螺旋钻具离散元截割模型Fig.3 Discrete element cut-off model for auger drilling tools
煤岩颗粒的接触参数设置见表2。
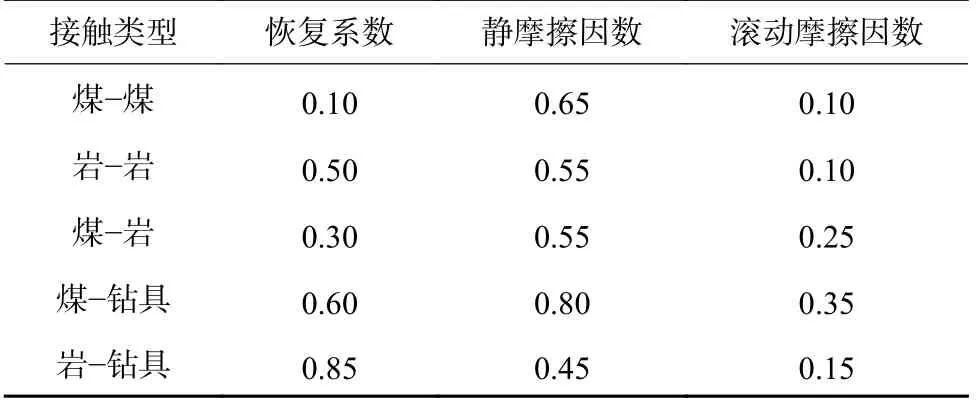
表2 煤岩颗粒的接触参数Table 2 Contact parameters of coal rock particles
煤岩颗粒间黏结键参数由下式进行估算[13]:
式中:kn与ks分别为法向刚度和切向刚度系数,N/m2;r为颗粒半径,m; µ为泊松比;E为截割煤壁的弹性模量,Pa; σ为法向极限应力,Pa; τ为切向极限应力,Pa;φ为内摩擦角,(°);C为黏聚力,Pa。
所建煤壁中煤岩颗粒直径均为20 mm,钻具材料默认金属钢,导入钻头三维模型后进行截割模拟。
针对煤岩硬度、钻头截割转速与钻头进给速度3 个影响因素共计建立27 组离散元截割模型,钻具钻采深度均为0.75 m,模拟完成后提取各工况下钻具的截割扭矩并计算不同工况下的扭矩均值,计算结果见表3。
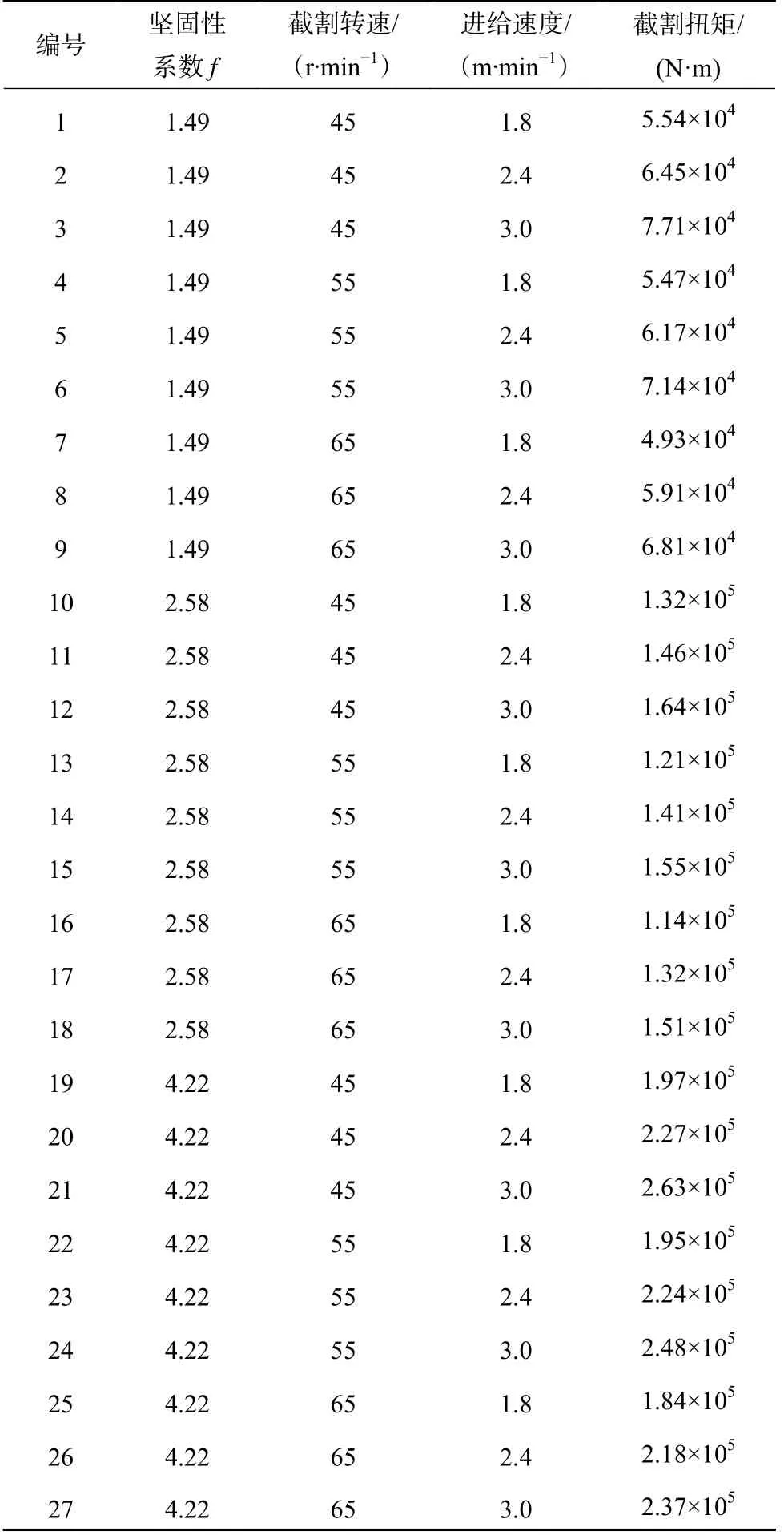
表3 不同仿真方案对应的截割扭矩Table 3 Cut-off torque for different simulation scenarios
根据不同仿真模型截割扭矩T与钻头转速n1的关系计算不同工况下钻头的截割功率Pc:
计算完成后,以钻头截割功率Pc为函数响应,以截割转速n、进给速度v与煤岩硬度f为变量建立多元回归函数,得到关于钻头截割功率的回归关系:
以钻具截割比能耗Hw对钻具开采经济性进行评价,截割比能耗反映了钻具开采1 m3煤岩过程中的能量损耗,对于煤矿企业来说,截割比能耗越小煤岩开采成本越低,开采经济性越好,截割比能耗的评价模型如下:
式中:t为钻头截割时间,s;Vc为所截煤岩体积,m3;R为钻头钻具半径,m。
2.2 钻杆输送比能耗分析
钻杆输送物料过程中物料相对钻杆的运动状态变化较小,对物料过程进行一定程度的简化,可以通过建立钻杆输送物料阻力模型求解来估算钻杆输送功率,再根据输送阻力与输送物料的体积关系计算钻杆输送物料时的能耗数值。
如图4 所示,当不考虑叶片摩擦时,螺旋面A点的圆周速度vb=πn2r/30沿螺旋面方向,n2为钻杆转速,绝对速度v0=vbsin α沿法线方向,由于物料与叶片间的摩擦因数 µ,使物料绝对速度vs方向偏离法向一个摩擦角 φ,对绝对速度vs进行分解可得到颗粒的圆周速度vc和轴向速度va[14]:
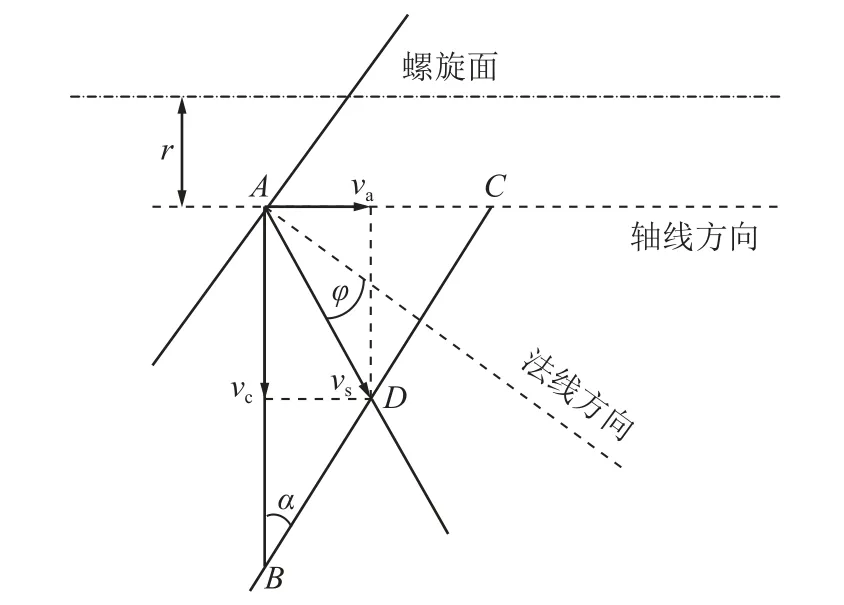
图4 物料运动速度分解Fig.4 Decomposition of particle motion velocity
根据物料速度的矢量关系可得出:
物料圆周速度vc和轴向速度va分别为
其中:
式中: α为螺旋升角,(°);S为螺距,m。
将上述各式代入式(9)可得轴向速度va:
式中:ra为钻杆外径R与导杆直径r的均值,m。
如图5 所示,螺旋钻杆输送物料过程中,钻杆需克服物料输送过程中各种阻力,所需克服的阻力主要包括物料与孔壁的摩擦力、物料与叶片的摩擦力、物料提升阻力以及轴承摩擦阻力[15-17]:
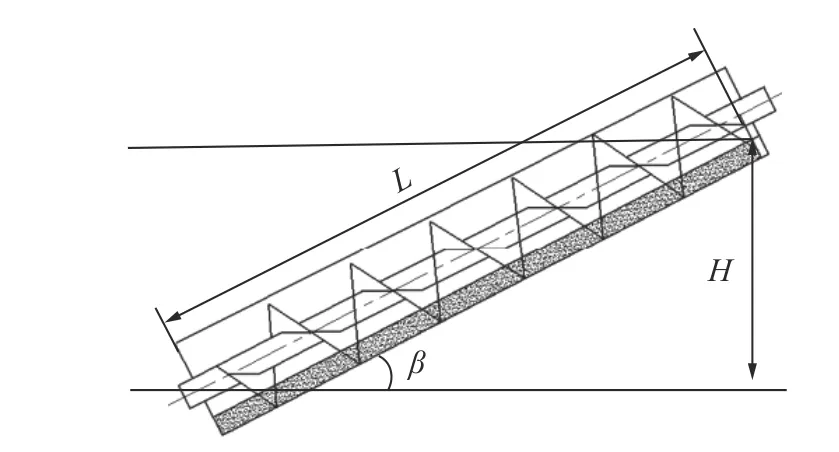
图5 螺旋叶片输送示意Fig.5 Schematic of spiral blade conveying
根据钻杆受力Fi与物料间相对运动速度vi的关系,可以计算钻杆用于克服阻力Fi的输送功率Pi:
1)克服物料与孔壁的摩擦功率P1:
其中,k0为阻力修正系数,对于磨磋性块状物料,取k0=1.2 ∼1.6,FL为单位长度的物料与孔壁的摩擦阻力,N/m。
其中:
其中:F为单位长度物料对钻孔的压力,N/m;L为钻采深度,m;fa为物料与孔壁的等效摩擦因数; β为输送倾角,(°);Fd为单位长度物料对孔壁底部的线压力,N/m;Fc为单位长度物料对孔壁侧边的线压力,N/m。
式中:Ac为物料输送过程中的横截面积,m2;h为物料层高度,m; γ为物料容积密度,kg/m3。
物料横截面积Ac随单位时间输送的物料体积发生变化,单位时间输送的物料越多,物料横截面积越大,物料对应的圆心角 θc越大,如图6 所示,物料截面积与对应圆心角的几何关系如下:

图6 物料圆心角示意Fig.6 Schematic of material rounding angle
钻杆物料截面积Ac与对应圆心角 θc的几何关系呈分段函数变化:
当0 ≤θc≤θs时:
当θs≤θc≤π时:
当π ≤θc≤2π-θs时:
当2π-θs≤θc≤2π时:
其中:h为物料横截面的高度,m;r为钻杆导杆的直径,m; θs为相切圆心角,rad; θp为钻杆导杆的圆心角,rad。
物料横截面的高度h与圆心角 θc的几何关系:
相切圆心角 θs、导杆的圆心角 θp与钻杆的几何关系:
如图7 所示,随着物料圆心角 θc增大,物料横截面积Ac不断增大,变化速率先增大后减小。
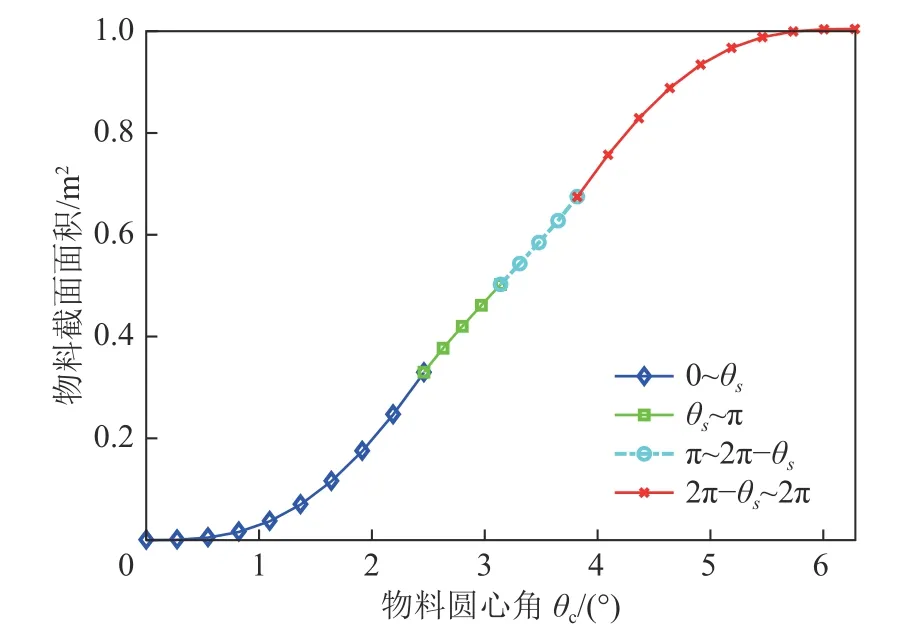
图7 物料截面积与圆心角函数关系Fig.7 Material cross-sectional area as a function of circular angle
根据物料截面积Ac与物料圆心角 θc的变化关系,可通过物料圆心角的变化来确定单位长度物料对钻孔的压力F,进一步计算可得克服物料与孔壁的摩擦功率P1:
2)克服物料与叶片的摩擦功率P2:
式中:fb为物料与叶片的摩擦因数。
3)克服物料提升高度功率P3:
4)克服轴承摩擦功率P4:
对于轴承的摩擦阻力,主要是由螺旋体质量引起:
式中:fc为轴承摩擦因数;G为每节螺旋体质量,kg;ds轴承平均直径,m;N钻杆节数。
钻杆克服上述能量消耗所需电机功率Ps:
式中:Ks为修正系数。
钻杆输送比能耗Sn数学表达式为
式中:Vs为输送体积,m3。
钻具单位时间开采能力与钻头进给速度呈正相关,而钻杆输送能力与转速呈正相关,如图8 所示,钻具进给速度2 m/min 条件下,钻杆较低钻速就能满足输送要求,即钻杆单位时间输送的煤岩体积高于钻头单位时间截割的煤岩体积。
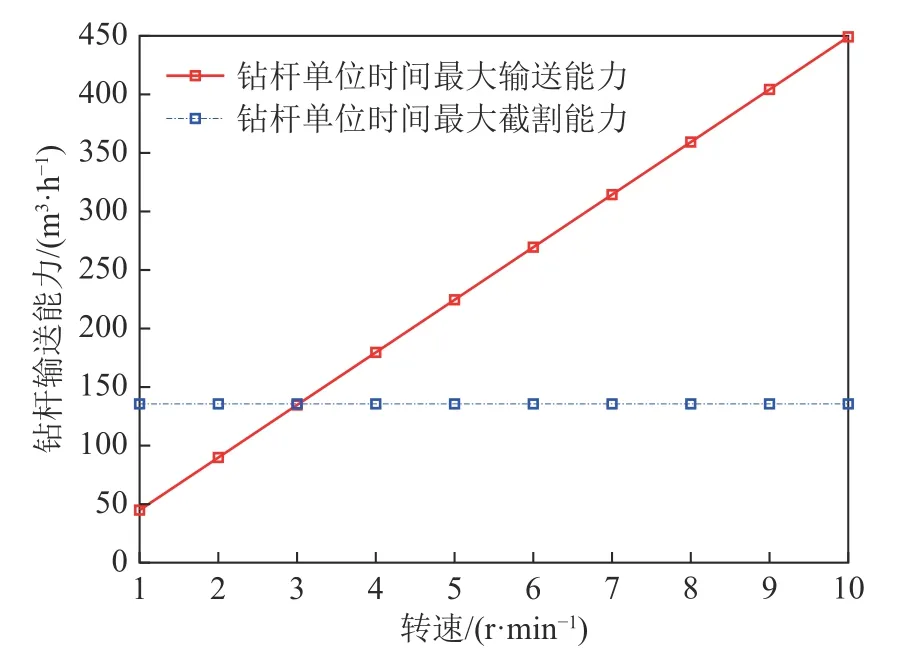
图8 转速对钻具截割与输送能力的影响Fig.8 Effect of rotating speed on cutting and conveying capacity of drill tool
由于截割后的煤岩由压紧密实状态到松散状态过程中体积会增大,为避免物料输送过程发生堵塞,需要通过提高钻杆钻速的方式增加钻杆输送容错能力。但当钻杆输送能力远高于钻头截割能力时就会造成钻杆无用功消耗量增加,不利于钻具的输送节能。钻杆实际工作过程中,增加转速能够有效提高输送能力,但钻头单位时间截割煤量不随钻杆转速发生变化,因此,钻具进给速度确定工况下,钻杆钻速增至一定值时,钻杆单位时间输送量将不再发生变化。
进给速度1.0 m/min 时,由于钻杆输送能力饱和,钻杆单位时间输送煤岩体积将不随钻速增加、钻采深度增加而发生变化,见表4。而随着钻杆转速增加钻杆单位时间的输送功率增大,钻杆输送比能耗增大,且钻采深度越大输送比能耗越大。
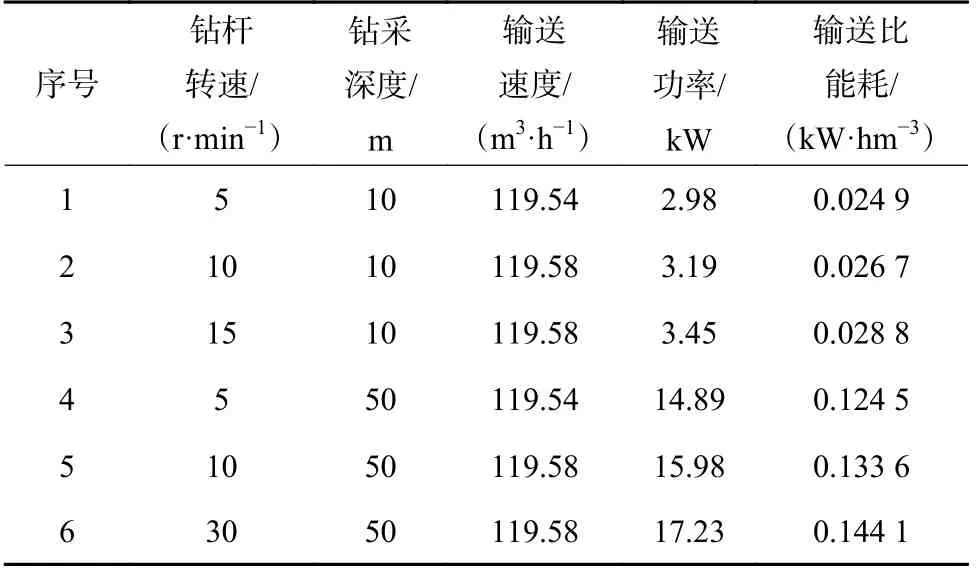
表4 不同工况钻杆转速与输送比能耗关系Table 4 Relationship between drill pipe speed and specific energy consumption under different working conditions
3 基于多目标优化的钻具协同控制模型
分离式钻具工作过程中,截割钻头先将煤岩体进行截割,破碎后的煤岩在螺旋钻杆作用下进行输送,钻头与钻杆间的运动状态对钻具内的煤岩输送状态相互影响,钻头单位时间截割煤岩体积若高于钻杆单位时间的输送能力,会增加钻杆堵转的风险,钻杆单位时间输送能力远高于钻头单位时间截割的煤岩体积将造成钻杆能耗浪费。
通过分析截割与输送的煤岩体积变化,获取钻头与钻杆间的内在联系,建立分离式钻具协同优化数学模型对实现钻具高效开采有着重要意义。如图9 所示,截割钻头前方煤岩未破碎前处于紧密状态,被截割破碎后煤岩由紧密状态变化为松散状态。
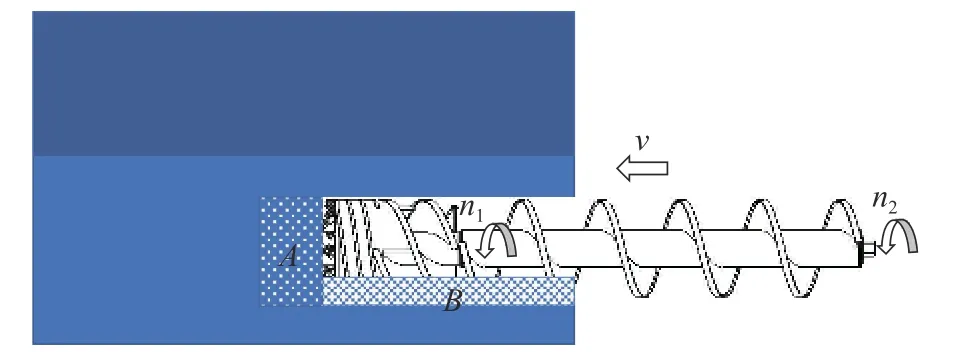
图9 煤岩状态变化示意Fig.9 Diagram of coal and rock state change
煤岩截割前紧实状态图10a,截割破碎后的松散煤岩图10b 通过钻杆进行输送,松散的煤岩在螺旋钻杆的输送作用下,输送煤岩的轴向距离增大,横截面积降低,煤岩截面积变化如图10 所示。
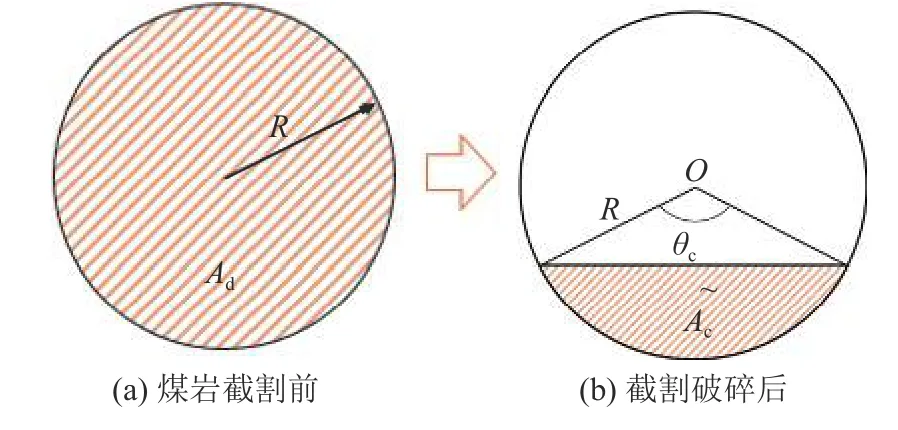
图10 煤岩截面变化示意Fig.10 Diagram of coal and rock cross section change
当截割钻头以v匀速向前推进, Δt时间内推进距离为Δl1=vΔt,钻杆转动过程中煤岩轴向移动距离为Δl2=vaΔt,由质量守恒定律[18-19]:
式中:Ad为钻头截割面积,m2; ρ为物料压实密度,kg/m3; γ为物料容积密度,kg/m3。
整理得:
当钻头进给速度不变,钻杆转动速度不发生变化时,钻杆上输送煤岩的横截面积不变。
联立式(31)与式(17)—式(20)建立钻具运动参数与物料圆心角之间的函数关系 θc的集合:
根据物料圆心角 θc可计算钻杆输送煤岩时的各项能耗。联立钻头截割能耗模型与钻杆输送能耗模型,以钻头截割比能耗Hw与钻杆输送比能耗Sn最小为优化目标,建立目标函数:
式中:K1为截割比能耗权重系数;K2为螺旋叶片输送比能耗权重系数。
取K1与K2权值:
分别以截割电机功率、钻具进给速度调整范围、煤岩填充率、截割电机与输送电机转速调整范围及物料输送圆心角为约束条件:
1) 电机功率约束。钻头截割与钻杆输送过程相对独立,动力传递效率与煤岩硬度不变条件下钻头最佳截割参数不随钻采深度的增加发生变化,而钻杆输送最佳转速会随钻采深度的增加不断变化。因此,钻具电机功率约束策略上保持钻头恒功率截割,而根据开采工况不断调整钻杆的输送功率,始终保持钻杆输送能力与钻头开采能力相匹配。
随着钻采深度的增加钻杆连接数量不断增加,钻杆传动的机械效率逐渐降低,机械传递效率与钻杆节数间的数学关系如下:
式中: ηL为相邻钻杆间的机械传递效率;m为钻杆联接节数;l为每节钻杆长度,m。
当电机额定功率Pd不变时,随着钻杆连接数量的增加,钻头与钻杆的实际功率均下降,即:
2) 电机转速约束。大口径螺旋钻机实际开采过程中通常通过降低钻具转速的方式提高钻具的截割能力,另一方面大口径钻具高速转动会带来剧烈的振动,因此螺旋钻机通常旋转速度较低:
3) 推进速度约束。螺旋钻具由推进油缸推动钻具向煤岩层截割,该过程推进油缸需提供足够的推进力,通常推移速度不宜过大:
4) 填充系数约束。钻杆输送物料过程中物料的填充系数不超过许用最大填充系数 [ψ]:
即物料圆心角 θc不超过 π,物料横截面积Ac不超过π(R2-r2)/2:
5) 钻杆输送能力约束。为保证钻杆内输送物料不发生堵塞,钻杆输送能力要高于钻头截割能力,确保钻头截割的煤岩能够及时输送:
4 分离式钻具协同控制能耗分析示例
以钻头截割比能耗与钻杆输送比能耗最小为目标建立了分离式钻具协同优化模型,所建协同优化数型中优化参数包括钻头转速、输送转速与钻具进给速度,输入参数包括煤岩硬度、钻采深度与开采倾角。其中,煤岩硬度、钻采深度与开采倾角作为开采工况已知条件。协同优化模型根据已知开采工况去优化钻头与钻杆的运动参数。
选择多种工况对分离式钻具协同优化效果与传统钻具的优化效果进行对比,其中传统钻具优化模型中钻头转速与钻杆钻速一致,模型优化目标与约束条件均与分离式协同优化模型一致。对硬度f=1.49 的均质煤层水平截割工况进行优化分析,其中,钻头初始转速45 r/min,钻具初始进给速度1 m/min,模型其余参数如下:
分离式钻具机械传动损失包括内杆与内杆的机械传动损失以及钻杆与钻杆的机械传动损失,而传统钻具的机械损失只包含钻杆与钻杆间的机械传动损失,当分离式钻具的截割电机额定功率130 kW,输送电机额定功率20 kW;取传统钻具截割电机额定功率150 kW 时,2 种钻具额定功率下的功率损失计算如下:
式中:P′为传统钻具损失功率,kW;PEe为电机额定功率,kW;P′′分离式钻具功率损失,kW;PE、Pe分为截割电机与输送电机额定功率,kW。
钻采深度相同时,2 种钻具额定功率工作时机械传动损耗功率相同,由于钻杆输送功率可以随输送负载不断调整,相同工况下分离式钻具机械传统损失会略低于传统钻具。
为研究分离式钻具协同控制效果,分别对10、30 与50 m 钻深工况进行优化结果分析,利用钻具协同控制模型对传统钻具与分离式钻具截割参数进行优化,其中,传统钻具优化模型中钻头转速与钻杆转速保持一致,截割与输送总功率低于150 kW,分离式钻具的截割电机功率不超过130 kW,输送电机功率不超过20 kW。利用遗传算法对模型优化参数进行求解,遗传算法求解中群体大小设置20,交叉概率设置0.4,变异概率设置0.01,遗传算法终止迭代次数设置50 次,新型钻具钻采10 m 时遗传算法收敛曲线如图11 所示,采用遗传算法求解钻具优化参数具有良好的收敛性。
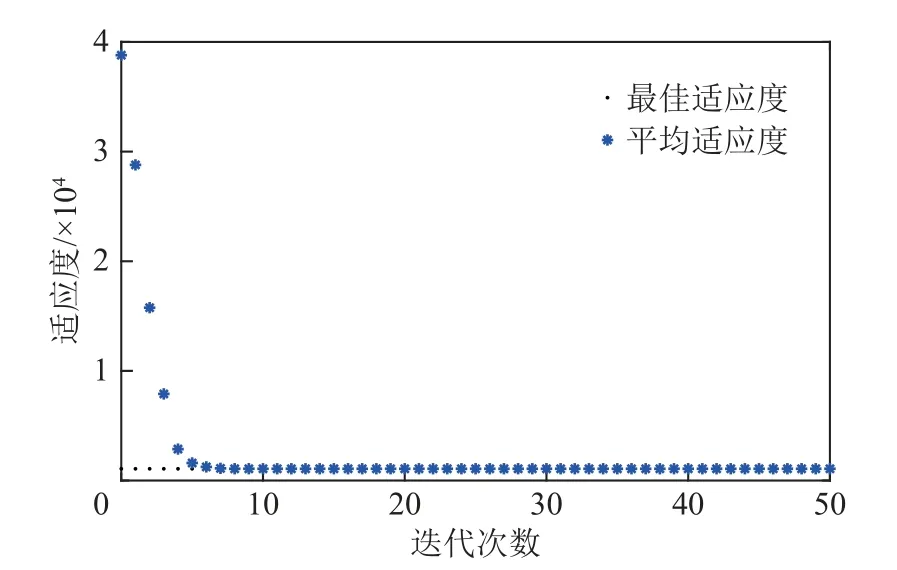
图11 遗传算法收敛曲线Fig.11 Genetic algorithm convergence curve
分别对传统钻具与新型钻具在不同钻采深度下的钻具工作参数进行优化,优化结果见表5。
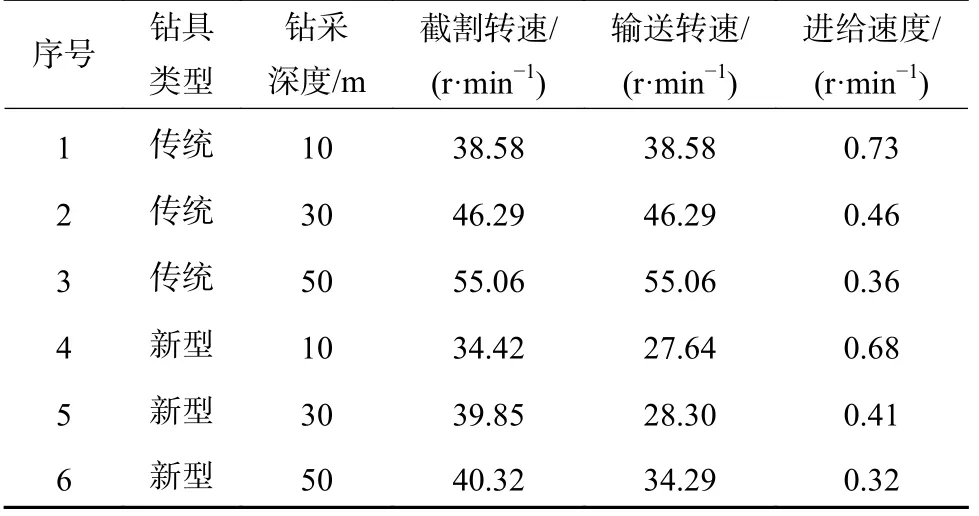
表5 两种钻具不同钻采深度下的运动参数优化结果Table 5 Kinematic parameter optimization results of two kinds of drill tools at different drilling depths
优化结果显示,装机总功率一致下,传统钻具能够利用装机功率集中优势提高钻具的进给速度,增加钻具单位时间的开采效率,而分离式钻具能够通过降低钻杆转速的方式降低钻杆输送功率从而弥补截割电机的功率损失。
随着钻采深度的增加,2 种钻具的截割比能耗与输送比能耗均增大,其主要原因是随着钻采深度的增加,钻杆连接节数增多,系统传动损耗功率增大导致钻头截割过程中的有效功率减小,另一方面,随着钻杆节数的增多,钻杆转动过程需克服的阻力增大,钻杆输送过程中的有效功率比值减小,见表6。
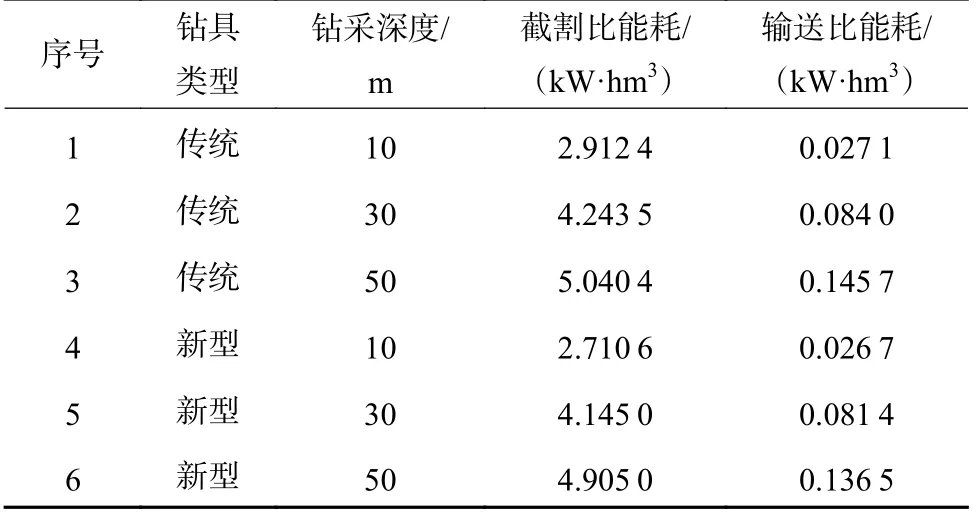
表6 优化后的钻具性能Table 6 Optimized drill performance
相比于传统钻具,分离式钻具拥有更好的能耗优化结果,在钻采深度10、30 与50 m 条件下,分离式钻具截割比能耗优化结果分别比传统钻具低6.92%、2.32%与1.88%,输送比能耗分别低1.47%、3.09%与6.31%,随着钻采深度的增加分离式钻具在输送比能耗上的优势逐渐体现。
5 分离式新型钻具制备与试验测试分析
为进一步验证分离式钻具对解决螺旋钻具截割转速与输送转速不匹配问题的有效性,通过制备分离式新型钻具实物模型,搭建分新型钻具试验测试平台,以试验的方式进行效果检验。
根据图1 分离式新型钻具的设计图纸制备钻具实物模型,其中制备钻具直径200 mm,钻具内杆直径65 mm,钻杆长度840 mm,叶片螺距250 mm,钻具整体质量10.34 kg,钻具试验测试平台如图12所示。

图12 新型钻具试验测试装置Fig.12 New drill test device
测试装置包括钻头截割电机、钻杆输送电机、电机变频器、转速-转矩-功率传感器、截割煤仓与信号采集系统。如图13 所示,测试装置通过螺旋钻杆中的内杆驱动截割钻头转动;通过链条传动的方式驱动钻杆转动;通过滚珠丝杠控制钻杆轴向移动,钻头与钻杆的速度变化均通过变频器控制实现。

图13 试验测试装置局部结构组成Fig.13 Test device local structure composition
钻头最佳截割参数随截割煤岩的硬度、电机输送功率等因素不断发生变化,为验证分离式钻具协同优化效果,需要建立钻头截割能耗模型与钻杆输送能耗模型,考虑试验周期和试验成本,通过向煤仓填充煤矸模拟煤岩开采情况,利用透明亚克力管道模拟钻孔煤壁,对钻头截割管道内煤矸与钻杆输送煤矸过程进行协同试验研究,试验工况如图14 所示。

图14 分离式钻具截割输送试验工况Fig.14 Test condition of separated drill tool cutting and conveying
通过改变钻头转速与进给速度多次试验,采集不同工况下钻头截割功率,当钻头截割功率平稳后,取功率平均值作为钻头当前工况下的截割功率,钻头截割试验方案与功率测量结果见表7。
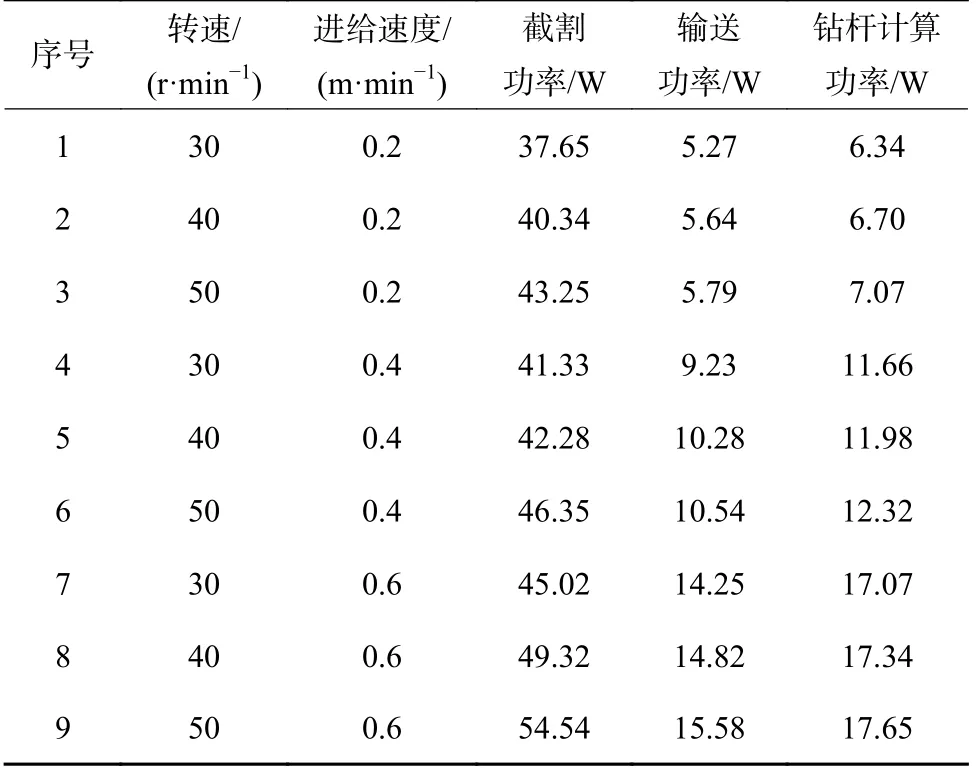
表7 钻头截割试验与测量功率Table 7 Bit cutting test and measuring power
以钻头截割功率为函数响应,以钻头截割转速nt与进给速度vt为变量进行多元回归拟合,得到当前工况下钻头的截割功率Pt的回归关系:
钻杆输送计算功率与实际测量功率偏差最大误差为26.23%,平均误差18.55%,通过调整功率修正系数Ks对输送功率数学模型进行修正,Ks调整为1.47。将试验所得当前工况下钻头截割功率回归关系替代式(5),建立当前钻头开采工况的截割能耗模型,将分离式钻杆结构参数带入钻杆输送能耗数学模型中建立当前工况下钻杆的输送能耗模型,分别以截割电机功率50 W,钻杆输送功率18 W 为约束,以当前工况下钻头截割比能耗与钻杆输送比能耗数值最小为目标,利用遗传算法对钻头截割钻速、钻杆输送转速以及钻具进给速度进行优化求解,得到传统钻具与分离式钻具优化参数,并通过试验对优化后的参数进行试验验证,钻具优化参数与对应截割比能耗、输送比能耗的结果见表8。
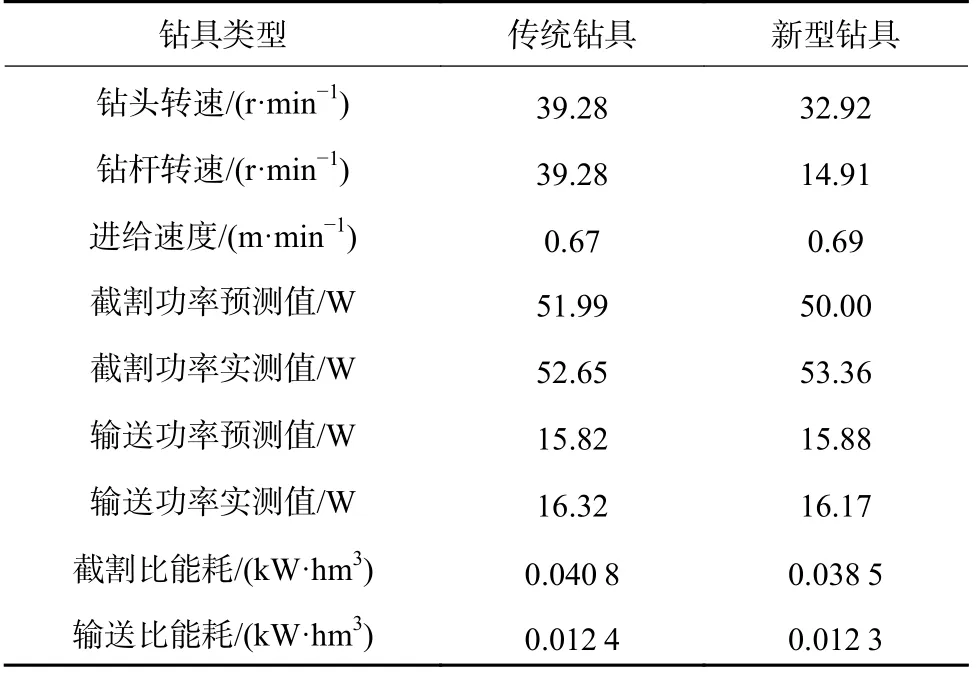
表8 两种钻具截割参数优化结果与性能评价Table 8 Optimization results and performance evaluation of cutting parameters of two kinds of drill tools
对2 种钻具优化结果进行对比分析,钻头与钻杆同速转动时截割与输送实测总功率为67.81 W,与预设偏差0.3%,钻头与钻杆差速转动时截割与输送实测总功率为66.17 W,与预设偏差2.7%,功率分配偏差较小,2 种钻具试验结果显示,相同工况下,分离式钻具比传统钻具拥有更好的开采性能,钻头与钻杆协同优化后进给速度提高了2.98%,截割比能耗降低了5.63%,输送比能耗降低了0.81%。
6 结 论
1)提出了新型分离式钻具结构,实现钻头截割转速与钻杆输送转速独立控制,解决了钻具最佳截割转速与输送转速不匹配问题。
2)通过建立钻头截割与钻杆输送协同能耗优化模型,对钻头截割转速、钻杆输送转速以及钻具进给速度进行参数优化,优化结果显示,当钻具截割与输送总功率相同时,传统钻具利用功率集中优势能够提高钻具进给速度,增加钻具开采效率,而分离式钻具能够通过钻头与钻杆运动参数的协同优化,进一步降低钻具开采比能耗,并随着钻采深度的增加,分离式钻具低输送比能耗优势逐渐体现。
3)通过制造分离式钻具实物模型,利用试验的方法对分离式钻具协同优化性能进行验证,试验结果表明:相比于传统钻具新型钻具优化结果具有更好的节能效果,相同工况下,相比与传统钻具分离式钻具协同优化后进给速度提高了2.98%,截割比能耗降低了5.63%,输送比能耗降低了0.81%。试验验证了分离式钻具协同优化效果的有效性。

