我国东南地区Noah-MP 模式地表温度模拟参数化方案寻优研究

王云宇 沈润平 黄安奇 谢昭颖 邢雅洁 师春香 孙帅

1 南京信息工程大学地理科学学院，南京 210044

2 国家气象信息中心，北京 100081

1 引言

地表温度直接影响地表能量与水热交换，是陆气耦合的核心变量之一，也是全球气候变化研究的重要参数（王明娜等, 2016; 李一玲等, 2018; Long et al., 2020）。由于陆面过程模型建模和参数化方案的不确定性，在陆面模式中准确模拟地表温度仍然存在挑战（He et al., 2021）。随着物理过程研究的不断成熟，陆面模式已从代表能量平衡的简单水桶模型，发展到能够考量物理、化学和生物过程之间相互作用和反馈的复杂模型，使得地表温度的区域尺度模拟成为可能，并可以为同样的过程提供多种方案（Manabe, 1969; Dickinson et al., 1986; Sellers et al., 1986, 1996）。其中，Noah-MP（Noah land surface model with Multi-Parameterizations）对Noah 陆面模式进行了大量改进，在此基础上耦合了多种不同的陆面模式中的植被冠层、辐射传输和水文模块，从而被广泛使用（Niu et al., 2011; Ma et al., 2017）。但在陆面模式模拟过程中，往往存在难以确定合适的参数化方案组合问题，不同参数化方案的选择导致了模式模型差异，从而成为模型结构和模拟不确定性的主要来源（Clark et al., 2011; Cai et al., 2014）。

对参数化方案进行系统评估与寻优，将有利于加强理解模型在不同区域的表现与提升模拟性能，确定在不同地表类型与不同季节模式模拟的主导过程与最佳组合。目前，已有研究在不同的下垫面或气候类型进行了Noah-MP 模式模拟研究，并采用不同方法量化不同参数化方案的模拟性能，并优化了参数化方案组合（叶丹等, 2017; 尤元红等, 2019;胡泽超等, 2020）。如采用自然选择法与Tukey 检验法结合（Zhang et al., 2016; You et al., 2019），从参数化方案在“最优集合”与“最差集合”出现频次来判断其对模拟性能的影响。纳什效率系数（Gayler et al., 2014）、样板参照法（Chang et al.,2020）、泰勒技能评分法（Yang et al., 2021）等方法也常用于评估不同参数化方案的评估。然而，研究大都局限于单个气候类型或单个下垫面类别，且更多的研究集中于单点尺度的短期模拟。尽管基于Noah-MP 的研究显示有较好的模拟能力，但在区域尺度上，参数化方案不确定性的研究容易受限于陆面模式所需要的气象驱动和陆面特征数据集（Hong et al., 2014），设计全组合参数化方案实验，确定最优参数化方案，由于模式复杂，区域模拟计算运行时间长，计算量大，往往受计算能力和计算量限制（Gan et al., 2019），目前更多研究仅考虑单一或少量物理过程（孙帅等, 2017），更多的研究则是基于经验或默认选项，使用单一的和主观的方案组合，给模拟带来较大的不确定性。

针对目前参数化方案优化主要在单点进行，缺乏区域尺度参数化方案寻优研究，本文引入正交试验方法，进行模式参数化方案试验，以解决模型物理过程多，参数化方案复杂，模拟试验运算量大，难以全面实施的难题。研究选取动态植被、气孔阻抗过程、控制气孔阻抗的土壤湿度参数过程、表面热交换系数过程以及辐射传输过程5 个关键物理过程，设计了9 个典型参数化方案组合正交试验，以中国气象局陆面数据同化系统2.0 版本大气强迫数据（CLDAS-V2.0），驱动Noah-MP 开展地表温度模拟研究，以期找出东南地区地表温度模拟的最佳参数化方案，以促进我国CLDAS/Noah-MP 系统研究与应用。

2 模型、数据与方法

2.1 研究区域

我国东南地区位于107.5°E 以东，35°N 以南的区域，主要跨越河南、江苏、湖北、安徽、浙江、湖南、江西、广西、广东、福建、海南和台湾等省区，主要为热带和亚热带季风气候区域，年均气温约在16.3～25.7°C，区域主要植被类型为亚热带常绿阔叶林及针阔混交林。该地区是中国人口、城市群和产业等比较集中的区域，受季风气候影响强烈，地形复杂，地表植被多样，陆面状况的复杂性必然对陆面过程模式区域模拟提出更高要求（温飞等,2021）。

2.2 研究数据

2.2.1 大气强迫数据

中国气象局陆面数据同化系统是目前国内陆面数据同化系统领域唯一实时运行的业务系统CLDAS-V2.0（China Meteorological Administration Land Data System version2.0）（http://data.cma.cn/[2022-07-29]），CLDAS-V2.0 数据主要由质量控制后的2400 余个国家级自动站点以及40000 多个区域自动气象站，ECMWF、GFS 数值分析预报产品和风云二号（FY-2）卫星数据等，利用数据同化与多源融合技术，将地面观测数据、卫星观测产品及数值分析产品等进行多源数据融合，从而获取高质量的网格化地面2 m 气温、气压、2 m 相对湿度、10 m 风速、降水和辐射大气驱动数据，覆盖东亚区域（0～65°N，60°E ～160°E），空间分辨率为0.0625°（纬度）×0.0625°（经度），时间分辨率为1 h。该产品在中国区域比同类产品质量更高，且已被验证适用于不同模式的区域模拟（朱智等, 2017; 孙帅等, 2017; 韩帅等, 2017; 王智慧等,2020）。考虑到可获取的驱动数据限制，研究选择了2015 年作为研究时段。

2.2.2 模型静态输入数据

高程数据来自于2010 年全球多分辨率高程数据（ GMTED2010）（ http://earthexplorer.usgs.gov/[2022-07-29]），由美国地质勘探局（USGS）和国家地理空间情报局（NGA）通过融合11 种栅格数据源开发，覆盖90°S～84°N 范围，分辨率为30″。土地利用数据采用美国地质调查局发布的USGS 全球土地利用数据，分辨率为30″。土壤质地数据来源于世界粮食农业组织（FAO）联合许多土壤学家研制的覆盖全球的土壤资源数据库，分辨率为30″（https://www.fao.org//[2022-07-29]。将所有静态输入数据重采样至0.0625°分辨率，并投影至模型网格。

2.2.3 观测数据

研究使用的地表温度观测数据来自于国家气象信息中心所制作并提供服务的“中国国家级地面气象站基本气象要素定时值数据集（V3.0）”，该数据集基于中国2474 个国家级地面站数据更正后的月报数据文件（A0/A1/A）基础数据集制作而成。本文提取了研究区域内2015 年连续定时观测站点的地表温度观测数据，作为模式模拟评估数据，并去除异常值，提取站点下垫面信息（图1b），不考虑镶嵌像元，参考Huang et al.（2022a）的方法，整理为农田站点、林地站点、草地站点与灌木站点。其中，农田站点包括位于USGS24 分类体系中旱地农田牧场和灌溉农田牧场的观测站，草地站点包括位于草地和热带稀树草原的观测站，灌木站点为位于灌木的观测站，林地站点包括位于落叶阔叶林、常绿针叶林，常绿阔叶林和混交林的观测站点。

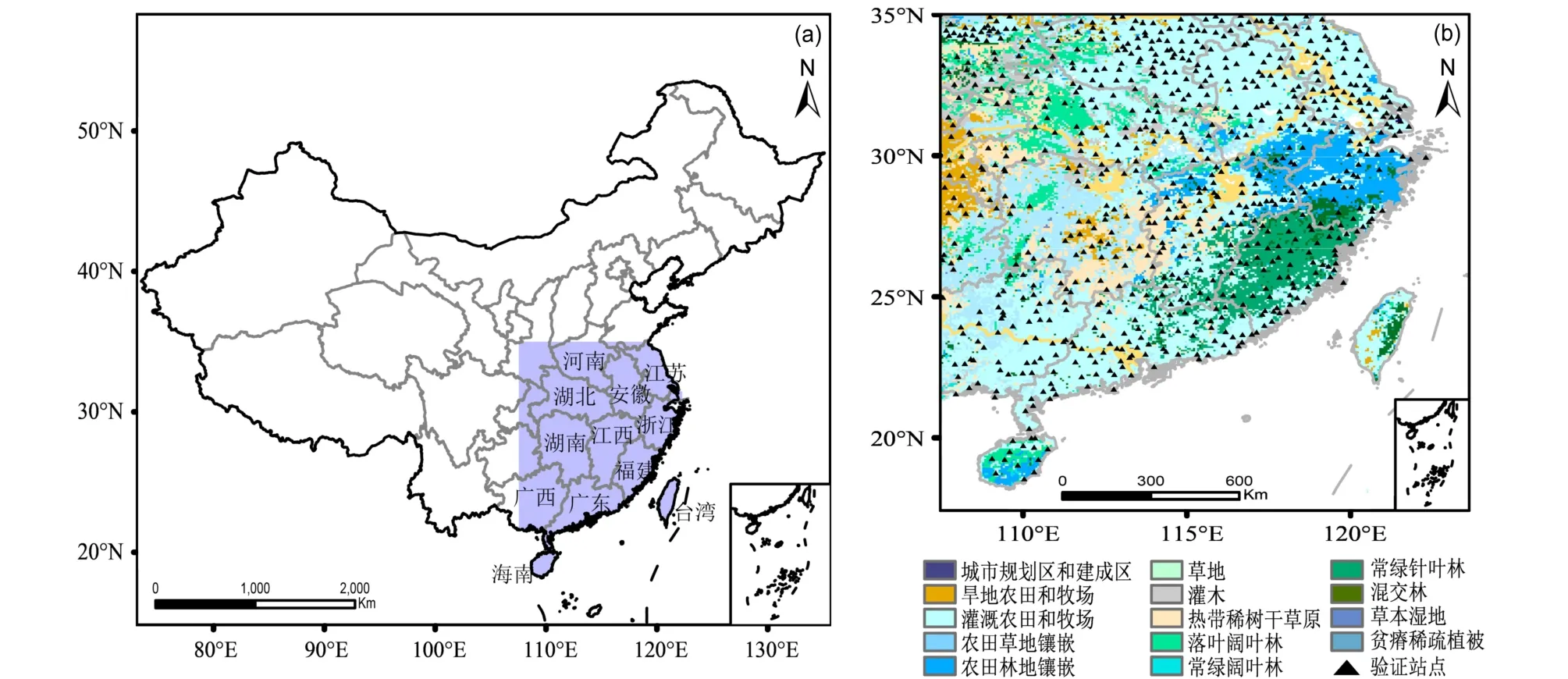
图1 我国东南地区（a）研究区域与（b）USGS（美国地质勘探局）土地利用类型分布Fig. 1 Distributions of (a) the study area and (b) USGS (United States Geological Survey) vegetation types over Southeast China

2.3 模型与方法

2.3.1 Noah-MP 物理过程及参数化选项

Noah-MP 陆面模式是基于Noah 陆面模式发展而来的，具有多个参数化方案选项来模拟植被—土壤—大气系统能量、动量和物质相互作用过程的陆面模式，同时也是CMA 陆面数据同化系统的主要陆面模式之一，具体物理过程及参数化方案改进见Niu et al.（2011）。本研究从地表能量平衡方程出发，考虑到我国东南部地区陆面主要过程实际和模拟参数，选取与地表温度直接相关的5 个关键物理过程进行分析，包括动态植被模块（DVEG）、冠层气孔阻抗过程（CSR）、控制气孔阻抗的土壤湿度参数过程（BTR）、表面热交换系数过程（SFC）和辐射传输过程（RAD）。对于其他物理过程的参数化方案本文根据Niu et al.（2011）的建议进行设置：（1）SIMGM 方案径流与地下水，（2）NY06 方案的过冷水过程，（3）NY06 方案的冻土渗透过程，（4）CLASS 方案的雪表反照率，（5）Joradn91 方案的雨雪分离过程，（6）Noah方案的土壤温度下边界条件以及（7）半隐式的雪/土壤温度时间条件。表1 为选取的5 个物理过程及其参数化方案。

表1 本研究评估的物理过程及参数化方案Table 1 Noah-MP parameterization schemes investigated in this study

2.3.2 正交试验法

在医疗和农业等研究领域，正交试验方法为常用的优化试验设计方法（Liang, 2008; Xia et al.,2016; Wu et al., 2018），它根据数理统计学与正交性原则，在完全试验工作量较大时，优选出有代表性的试验点，建立“正交表”来进行试验，从而了解全面试验的情况，达到优化和减少试验的目的。在正交试验中把所考察的结果称为指标，把对试验指标可能有影响的参数称为因素，把每个因素在试验中要比较的具体试验条件称为水平。正交表是正交试验设计的基本工具，他必须满足以下两个条件：其一，每列的不同水平在试验中出现的次数相同；其二，任意两列的不同水平组合组成的数对在试验中出现的次数相同（董如何等, 2004; 何为等,2012）。这既保证了试验点分布的均匀性，也使得正交试验具备了分散性和整齐可比性，从而能够科学、全面地反映全面试验的结果。本研究引入该方法进行模式参数化方案试验研究，以解决模型物理过程多，参数化方案复杂，模拟试验运算量大，难以全面实施的难题。研究将物理过程作为试验的因素，对应的参数设置作为因素的水平，建立正交表。

由于动态植被模块（DVEG）的开启动态植被方案与冠层气孔阻抗过程（CSR）的Jarvis 方案具有对立性，即动态植被模块开启时，冠层气孔阻抗仅能选择Ball-Berry 方案，本文将动态植被模块与冠层气控阻抗过程看作一个具有三水平的因子考量，具体为水平1 表示为动态植被OFF 方案与气孔阻抗的Ball-Berry 方案（OFF-Ball-Berry）；水平2为动态植被ON 方案与气孔阻抗的Ball-Berry 方案（ON-Ball-Berry）；水平3 为动态植被OFF 方案与气孔阻抗的Jarvis 方案（OFF-Jarvis）。考虑到地表热交换系数因子仅有两水平，运用拟水平法（刘永政和钱尚玮, 1983）重复一次M-O 方案，即因子地表热交换系数水平1 与水平3 均为M-O 方案。本文借用L9（34）（其中9 为试验总次数，3为水平数，4 为因素数）的正交表建立模式模拟试验，正交试验因素水平与具体试验参数化方案组合如表2 和表3。

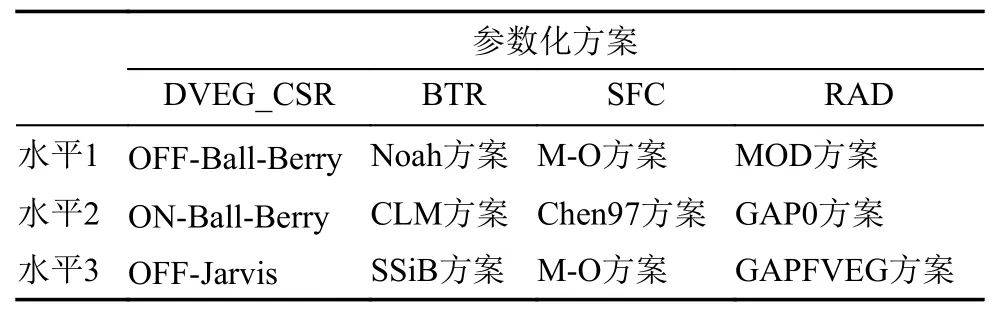
表2 正交试验中各因素水平对应的参数化方案Table 2 Parameterization scheme for each level of various factors in orthogonal test

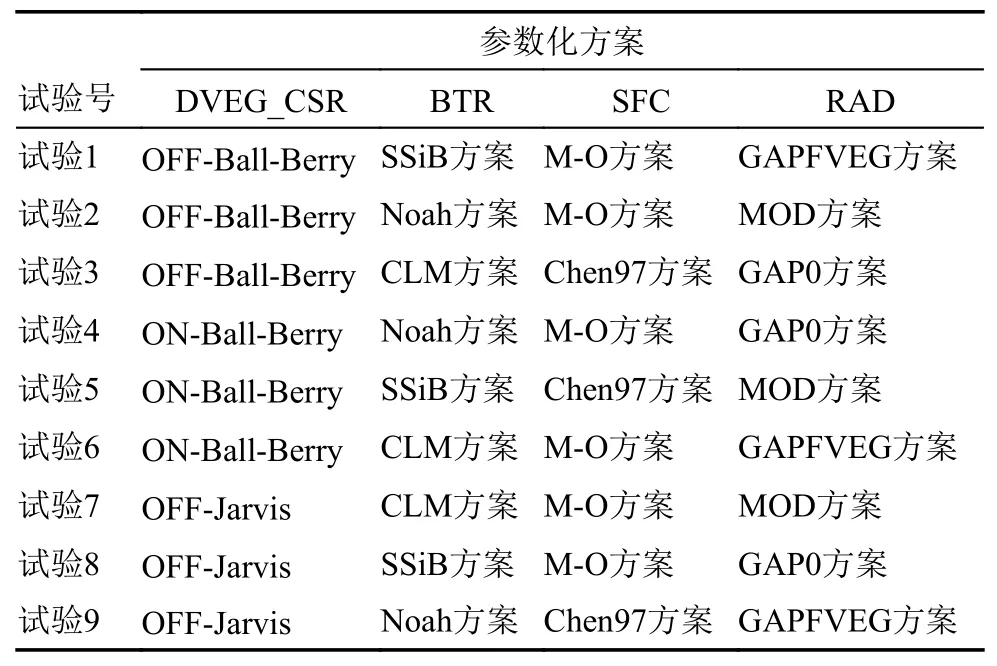
表3 正交模式模拟试验参数化方案组合Table 3 The setup of the orthogonal test

2.3.3 分析方法及评估指标

研究将模式输出的地表温度数据处理成日平均和月平均数据，并采用双线性插值的方法插值到观测站，使用偏差（δ）和无偏均方根误差（Sub）两个统计指标来分析模拟质量。具体公式如下：

其中，Si为模式模拟的地表温度数据，Oi为国家级气象站点的观测地表温度数据，N为样本个数。误差反映的是地表温度的模式模拟值与观测值之间的差异，出现正偏差表示模拟出现高估，负偏差表示低估。无偏均方根误差可以消除均方根误差的系统误差，其表示模拟数据的准确性，值越小说明模式模拟的地表温度越接近真实值。

为了解在不同条件下不同物理过程模式对地表温度模拟的敏感性，量化物理参数化方案之间的差异，选出不同条件中最优参数化方案配置，研究采用方差分析方法与极差分析方法对模拟的结果进行分析，并以模式模拟与站点观测地表温度的无偏均方根误差作为方差分析的指标，以9 次正交试验模拟的每个站点的季节平均无偏均方根误差，视作一轮正交试验的重复试验，进行方差分析与极差分析。

（1）方差分析法

总偏差平方和QT反 映了该组数组的离散程度：

因素A的 偏差平方和QA为

其中，n为 正交试验次数。q为 水平数，Ki为该因素的第r个水平试验指标的和，a为每个水平的试验次数。令QM为所有因素的偏差平方和，则试验误差平方和QE为

各因素自由度fA、总自由度fT和误差自由度fE公式为

平均偏差平方和MA、误差平均偏差平方和ME和F比公式为

方差分析表中，根据其均方差的大小，判断因素影响的主次，均方差大则为主要因素；均方差小的为次要因素，并同时能据此得出试验误差的大小。研究将物理过程均方差通过归一化计算其敏感性得分，得分越高，表示其敏感性越强。显著性是根据选择的置信度（或称显著性水平）的大小、因素自由度和误差自由度等3 个变量来计算，并将F值与F临界值表作对比，PR（＞F）表示F 值所对应的显著水平α。研究使用显著性水平α=0.05，当PR＜0.05 时即认为该因素对结果影响显著，而当0.05＜PR 时表明该因素对结果影响不显著。

归一化敏感性得分SA为

为进一步量化物理过程间敏感性差异，研究分别在不同下垫面和季节进行归一化敏感性得分计算，物理过程得分越高，表示在该情况中对地表温度模拟越敏感。

（2）极差分析法

极差分析又称直观分析法，可以了解每个因素的试验指标的影响，并选择每个因素的最佳水平方案。其基本原理如下：

因素A中的i水平的极差评分记作

其中，Si为模式模拟的地表温度数据，Oi为国家级气象站点的观测地表温度数据，N为样本个数，s为正交表所有试验因素A中i水平出现的次数。根据指标的情况选定每个因素的最佳水平。本采用无偏均方根误差作为极差分析的指标，评分越低，则代表模拟效果越好，对于通过敏感性检验的因素（物理过程），极差评分最小最小的水平为最优参数化方案，最后由每个物理过程的最低评分参数化方案，组成最优参数化方案组合。

3 结果与分析

3.1 正交试验模拟的总体分析

图2 显示了不同下垫面下，9 次试验站点地表温度模拟月平均偏差箱线图，并统计求取了最小值、第一个四分位数、中值、第三个四分位数和最大值，以呈现试验结果的不确定性范围。从9 次模拟试验平均与站点计算的偏差中位数来看，农田站点的偏差中位数为－0.76°C，林地站点为－1.88°C，草地站点为－1.59°C，灌木站点为－1.24°C。其中，所有试验中偏差中位数在7 月和8 月份较低，在2 月最接近0°C。说明大多数试验表现出不同程度的低估，在7 月和8 月低估更为明显。这与孙帅等（2017）的研究结果相吻合。

图2 Noah-MP 模拟9 次正交试验（a）农田站点、（b）林地站点、（c）草地站点、（d）灌木站点地表温度月平均偏差Fig. 2 Bias between the Noah-MP simulated and the observed monthly average temperatures in nine ensemble experiments in (a) farmland sites, (b)woodland sites, (c) grassland sites, and (d) shrub sites

从偏差的变化范围（偏差最大值与最小值的差）来看，所有下垫面均在8 月的变化范围最大，7 月次之，偏差变化范围越大，表明不同试验间的偏差大，说明参数化方案组合的选择对7 月和8 月的地表温度模拟产生较大的影响。11 月和12 月的偏差变化范围较小，说明参数化方案组合的选择对试验对模拟影响相对较小。林地区域全年不同月份的偏差的变化范围均较大，呈现较大的不确定性，说明林地植被对参数化方案的选择更加敏感（Xue et al.,2010）。

3.2 物理过程的敏感性分析

为了分析地表温度模拟对物理过程敏感性，依据方差分析结果量化了不同物理过程的敏感性（图3）。其中，带★符号表示该情况物理过程通过0.05 显著性检验，对模拟影响显著，未通过显著性检验则表示物理过程对模拟没有显著影响。对于不同下垫面与不同季节，分别依据公式（12）计算了不同物理过程归一化敏感性得分，得分越高，表示其在该情况中对地表温度模拟越敏感。从图3 可以看出，地表温度模拟对物理过程的敏感性，同时受到下垫面和季节的影响。对于农田区域， DVEG_CSR过程（动态植被与气孔阻抗过程）与SFC 过程（表面热交换系数）在所有季节都通过0.05 显著性检验，始终表现对地表温度模拟有显著影响。而BTR 过程（控制气孔阻力的土壤湿度参数）和RAD 过程（辐射传输过程）仅在春季、夏季和秋季通过0.05 敏感性检验，对模拟影响显著，但在冬季未则没有表现出显著性。其中，在春季，SFC过程归一化敏感性得分最高，说明其为最敏感的物理过程。在夏季、秋季和冬季，DVEG_CSR 过程的归一化敏感性得分最高，为最敏感的物理过程。

图3 春季（第一列）、夏季（第二列）、秋季（第三列）、冬季（第四列）不同下垫面动态植被与气孔阻抗过程（DVEG_CSR）、控制气孔阻力的土壤湿度参数过程（BTR）、表面热交换系数过程（SFC）、辐射传输过程（RAD）敏感性得分（带★表示该情况物理过程通过显著性检验）：（a-d）农田；（e-h）林地；（i-l）草地；（m-p）灌木Fig. 3 Sensitivity scores for DVEG_CSR, BTR, SFC, and RAD processes on different underlying surfaces in spring (first column), summer (second column), autumn (third column), and winter (fourth column): (a-d) Farmland; (e-h) woodland; (i-l) grassland; (m-p) shrubs

在林地区域，DVEG_CSR 过程与RAD 过程在所有季节均通过了0.05 显著性检验，表现出对模拟均有显著影响。BTR 过程在全年所有季节均未通过0.05 显著性检验，对地表温度模拟无显著影响。SFC 过程在春季、夏季与秋季通过敏感性检验，表现出显著影响，而冬季则对模拟的影响不显著。在春季和夏季，DVEG_CSR 过程的归一化敏感性得分最高，为最敏感的物理过程。秋季和冬季，则是RAD 过程得分更高，表现最敏感。

在草地区域，仅有DVEG_CSR 过程在所有季节都通过0.05 敏感性检验，对模拟影响显著。RAD 过程仅在夏季与秋季通过敏感性检验，对模拟影响显著。SFC 过程仅在夏季体现出显著性。而BTR 过程在所有季节都未能通过敏感性检验，对模拟无显著影响。其中，在所有季节DVEG_CSR过程的归一化敏感性得分始终较高，表现为最敏感的物理过程。

在灌木区域，DVEG_CSR 过程与RAD 过程在春季与夏季通过了0.05 显著性检验，对模拟影响显著。而BTR 过程与SFC 过程仅在夏季通过敏感性检验，表现出显著影响。所有物理过程在秋季与冬季均没有通过0.05 显著性检验，说明在秋季与冬季所有过程的参数化方案均没有体现出显著差异。DVEG_CSR 过程在春季与夏季的归一化敏感性得分更高，为较为敏感的物理过程。

除了春季的农田与秋、冬季的林地地区外，DVEG_CSR 过程的敏感性得分均最高，为最敏感的物理过程。这是因为动态植被ON 方案考虑植被通过光合作用、将吸收碳分配到每个碳库以及每个碳库的呼吸作用等动态输出LAI，而动态植被OFF 方案则通过查找参数表方案则给特定植被每月指定相同的LAI（Dickinson et al., 1998; Niu et al.,2011）。LAI 通过控制植被的生物物理特性影响地表能量平衡，这种差异在模式中极大影响了包括辐射、感热、潜热和地表热通量，从而改变了地表温度模拟（Huang et al., 2022b）。

3.3 不同下垫面不同季节最佳参数化方案

正交试验的极差分析可以确定每个因素（物理过程）的最佳水平（参数化方案），得出最佳参数化方案组合。图4 中不同的折线代表不同的物理过程，折线中的节点数值代表其不同参数化方案的极差评分（例如BTR 过程的折线从左至右3 个节点分别代表Noah、CLM、SSiB 方案的评分），评分越低则表示参数化方案模拟结果越好。未能通过0.05 敏感性检验的物理过程，说明其参数化方案选取对模拟结果没有显著影响。从图4 可以看出，地表温度模拟的最佳参数化方案组合，同时受到下垫面和季节的影响。在农田区域，DVEG_CSR 过程的ON-Ball-Berry 方案在春季、夏季与秋季极差评分较低，优于其他方案，在冬季则是OFF-Ball-Berry方案更好，这可能是因为ON-Ball-Berry 方案在冬季产生较低的LAI 和GVF（植被覆盖率），造成模拟偏差（Kucharik et al., 2006; Yang et al., 2011）。BTR 过程中Noah 方案较CLM 与SSIB 方案在春季、夏季与秋季极差评分更低，是较优的方案，BTR 过程在冬季未能通过显著性检验，3 种方案没有体现出显著差异。SFC 过程中，M-O 方案在所有季节的极差评分都低于Chen97 方案，表现更优。对于RAD 过程，GAPFVEG 方案在春季、夏季与秋季极差评分均最低，为最优方案，可能由于GAPFVEG 方案产生的冠层下太阳辐射最大，可以一定程度缓解了模拟的低估（Gan et al., 2019; Yang et al., 2021）。而RAD 过程在冬季表现不显著，参数化方案的选择对模拟结果无显著影响。

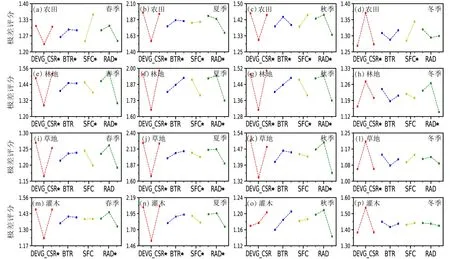
图4 同图3，但为不同季节下垫面参数化方案极差评分Fig. 4 Same as Fig. 3, but for the results by range analysis of orthogonal experiments of different vegetations in different seasons

在林地区域，DVEG_CSR 过程的ON-Ball-Berry 方案仍然在春季、夏季和秋季极差评分更低，表现更好，冬季则是OFF-Ball-Berry 方案更优。BTR 过程所有季节均未通过敏感性检验，其方案选取对模拟无显著影响。SFC 过程中，Chen97 方案在春季、夏季和秋季的极差评分低于M-O 方案，为较优方案，而在冬季两种方案没有体现出显著差异。RAD 过程在四季始终是GAPFVEG 方案评分较低，优于其他方案。

在草地区域，DVEG_CSR 过程与BTR 过程最优方案表现与林地相同。SFC 过程中，Chen97 方案极差评分在夏季低于M-O 方案，为较优方案，而在春季、秋季和冬季没有体现出显著差异。RAD 过程中，GAPFVEG 方案在夏季与秋季评分低于其他方案，依旧是最优方案，在春季与冬季各种方案对模拟影响不显著。

在灌木区域，DVEG_CSR 过程的ON-Ball-Berry 方案和RAD 过程的GAPFVEG 方案在春季和夏季的极差评分分别更低，为最佳方案，秋季与冬季则均未通过敏感性检验，方案选取对模拟影响不显著。BTR 过程的Noah 方案和SFC 过程的Chen97 方案在夏季极差评分分别较低，为最佳方案，其在春季、秋季与冬季各种参数化方案所有体现出显著差异。

综上分析，根据极差评分可得出不同下垫面在不同季节模拟的最优参数化方案如表4 所示。在农田区域的春季、夏季和秋季的模拟中，最优方案组合选用DVEG_CSR 过程的ON-Ball-Berry 方案，BTR 过程的Noah 方案，SFC 过程的M-O 方案以及RAD 过程的GAPFVEG 方案。在林地地区的春季、夏季和秋季以及灌木区域夏季的模拟中，最优方案组合为DVEG_CSR 过程的ON-Ball-Berry 方案，BTR 过程对林地影响不敏感，灌林区夏季则为Noah 方案，SFC 过程的Chen97 方案以及RAD过程的GAPFVEG 方案。考虑到物理过程未通过0.05 敏感性检验，其参数化方案选择无显著差异，上述两种方案也同样都满足草地区域在春季与秋季以及灌木区域在春季和秋季的表温度模拟的最优方案要求。同样在农田、林地和草地地区冬季的模拟中，则优化参数化方案组合可为DVEG_CSR 过程的OFF-Ball-Berry 方案， SFC 过程的M-O 方案以及RAD 过程的GAPFVEG 方案，此方案也适用于灌木区域冬季的表温度模拟，因为其所有的物理过程未通过0.05 敏感性检验，对参数化方案选择对模拟无显著影响。因此，在尽量减少参数化方案组合数量情景下，上述3 种参数化方案组合中有一种可能是适合研究区某种下垫面某个季节地表温度模拟的最优组合（表4）。

表4 不同下垫面不同季节的最优参数化方案Table 4 Optimal parameterization scheme of different underlying surfaces in different seasons

3.4 区域最佳参数化方案的验证

由于研究区下垫面复杂性，且一次陆面模式模拟中无法为不同的下垫面区域配置不同参数化方案，综合考量物理过程显著性与极差分析的结果，以上述综合得出的3 种可能的不同下垫面不同季节的最优参数化方案组合（表5）作为备选，在东南地区进行地表温度模拟比较试验，以期得出东南地区地表温度模拟的较为适合的参数化方案组合。

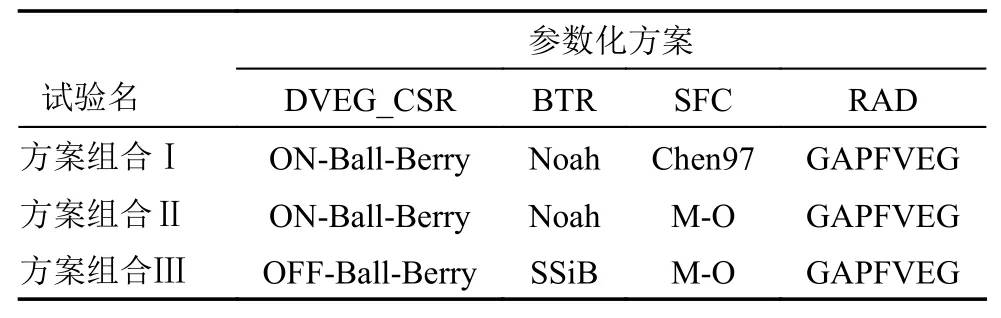
表5 3 个备选试验组合Table 5 Setup of the three optimization tests

3.4.1 空间误差分布

从空间偏差分布来分析（图5a-5c），方案组合Ⅰ、Ⅱ在研究区北部站点主要呈现正偏差，方案组合Ⅰ偏差更大，而方案组合Ⅲ的站点主要表现为负偏差，中部地区的站点低估明显。从站点偏差分段分布分析（图6a），方案组合Ⅰ、Ⅱ和Ⅲ分别有66.4%、65.6%和38.3%的站点偏差出现在－1°C～1°C，方案组合Ⅰ和Ⅱ偏差绝对值表现更低，明显优于方案组合Ⅲ。从无偏均方根误差空间分布来看（图5d-5f），在研究区北部所有方案的站点无偏均方根误差较大，中部和南部相对较小。方案组合Ⅰ、Ⅱ和Ⅲ的站点平均无偏均方根误差分别为1.54°C，1.41°C 和1.56°C，以方案组合Ⅱ最小。从无偏均方根误差分段分布分析（图6b），方案组合Ⅰ、Ⅱ和Ⅲ分别有17.8%、31.0%和15.1%的站点无偏均方根误差偏差低于1.25°C，分别有51.0%、69.2%和41.9%的站点无偏均方根误差偏差低于1.5°C，方案组合Ⅱ中更多的站点表现出更低的无偏均方根误差和分布。

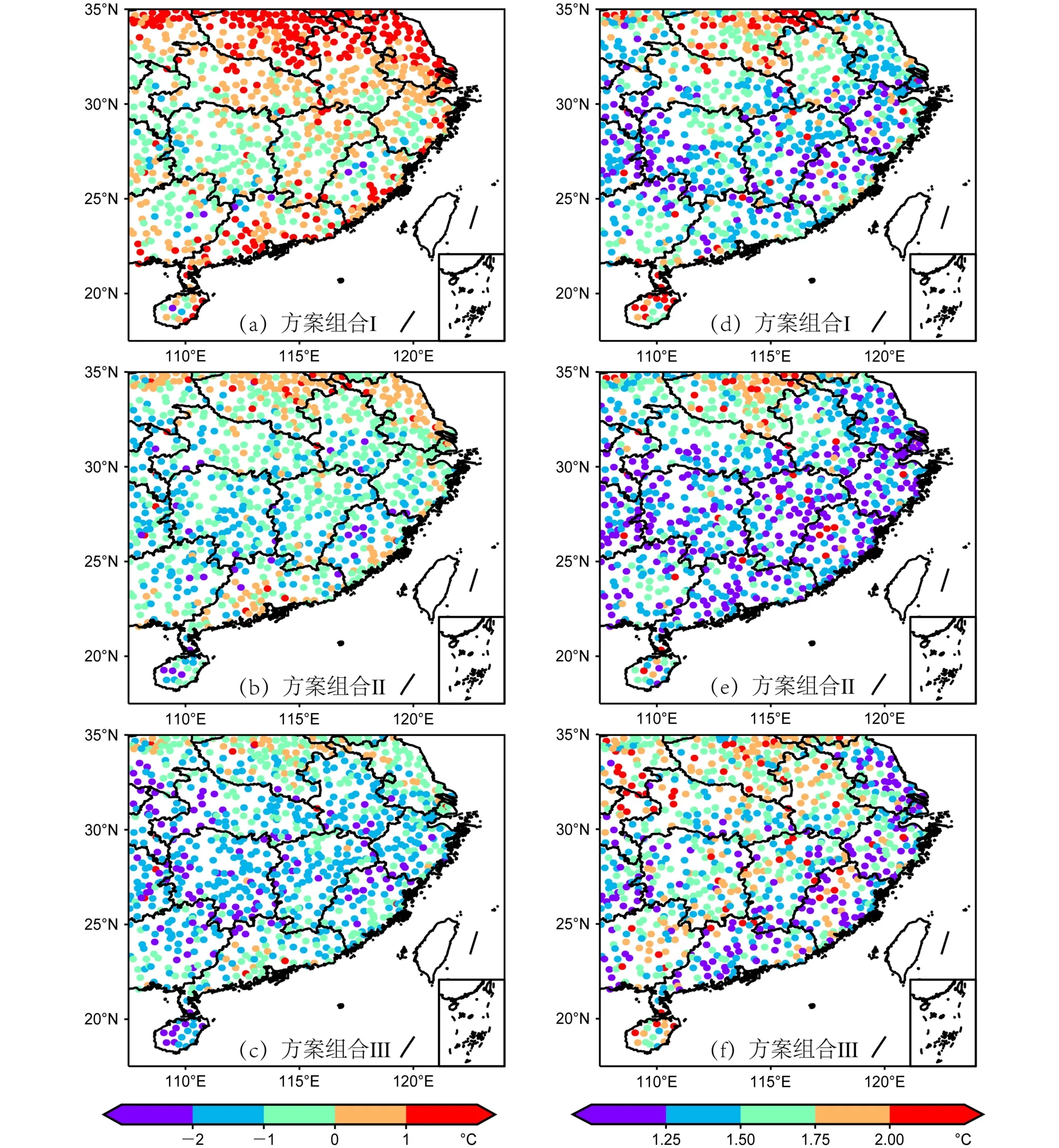
图5 方案组合（a、d）Ⅰ、（b、e）Ⅱ和（c、f）Ⅲ模拟地表温度的日均（a-c）偏差和（d-f）无偏均方根误差分布Fig. 5 Spatial distributions of (a-c) bias and (d-f) unbiased root mean square error between simulated and the observed daily average ground temperatures in scheme (a, d) Ⅰ, (b, e) Ⅱ, and (c, f) Ⅲ

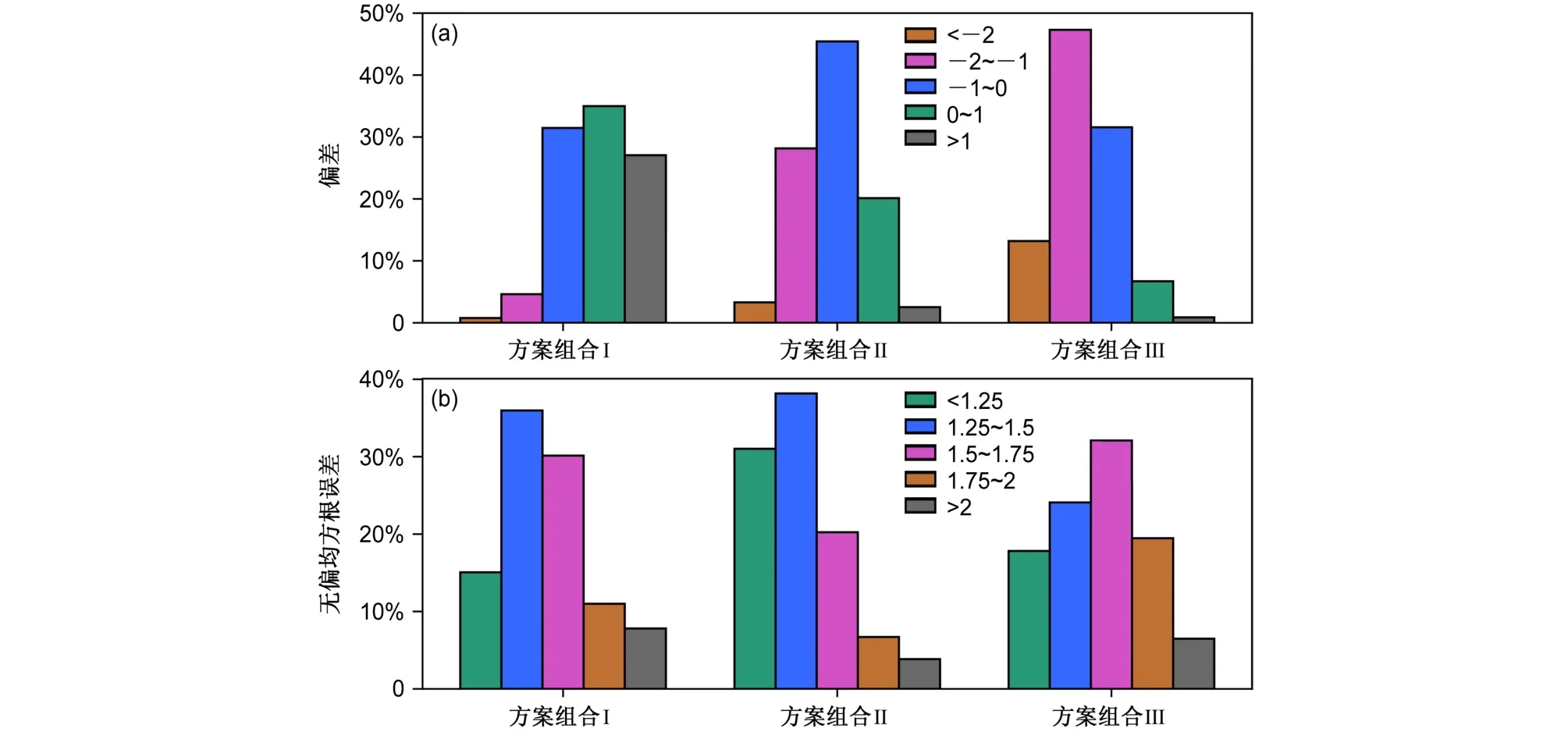
图6 方案组合Ⅰ、Ⅱ和Ⅲ的（a）偏差和（b）无偏均方根误差分布Fig. 6 Distribution of (a) bias and (b) unbiased root mean square error of the three schemes

3.4.2 时间序列误差变化

从日均偏差来看（图7a），方案组合Ⅰ有285 d偏差大于0°C，主要表现为正偏差，方案组合Ⅱ与方案组合Ⅲ分别有341 d 和357 d 偏差小于0°C，总体呈现为负偏差。从偏差绝对值分析，方案组合Ⅲ方案仅有168 d 偏差绝对值小于1°C，而方案组合组合Ⅰ、Ⅱ分别有308 d、298 d 偏差绝对值小于1°C，偏差绝对值较小。从日均无偏均方根误差来看（图7b），方案组合Ⅰ、Ⅱ和Ⅲ平均日无偏均方根误差分别为1.71°C，1.53°C 和1.58°C，以方案组合Ⅱ最小。

图7 方案组合Ⅰ、Ⅱ和Ⅲ模拟地表温度与观测日平均值的（a）平均偏差和（b）无偏均方根误差的时间序列（灰色部分为9 次正交试验模拟的结果范围）Fig. 7 Temporal distribution of (a) bias and (b) unbiased root mean square error between simulated and the observed average ground temperatures in the three schemes

从偏差与无偏均方根误差来看，3 种方案组合的差异主要来自于4～9 月。方案组合Ⅲ模拟的地表温度低估明显，这很可能是因为OFF-Ball-Berry给定的LAI 在植被生长季较高，增大了模拟的热通量，使得模拟的地表温度降低。而方案组合Ⅰ、Ⅱ的ON-Ball-Berry 方案则有效改善了生长季的模拟低估（Li et al., 2022; Huang et al., 2022b）。方案组合Ⅱ在研究区温度模拟较方案组合Ⅰ更低，这可能是由于使用零位移高度的M-O 方案比Chen97 方案产生了更大的感热通量（Niu et al., 2011; Gan et al., 2019），增加了地表与大气间的湍流热通量，对地表具有降温作用，一定程度上缓解了高估。

综上分析，方案组合Ⅱ拥有更低的日均无偏均方根误差，且从与9 次试验结果对比来看，方案组合Ⅱ在一年中有200 d 的无偏均方根误差低于9 次正交试验的最低值，表出更好的模拟效果。

4 结论

本文利用2015 年CLDAS-V2.0 大气强迫数据，驱动Noah-MP 模拟我国东南地区地表温度，将5个主要的关键物理过程（DVEG、CSR、BTR、SFC、RAD）与其他备选方案结合，借助正交试验法以完全考量参数化方案，通过9 次正交试验，结合方差分析与极差分析，确定适用于东南区域地温模拟的最优参数化组合，减少了CLDAS/Noah-MP模式在我国东南地区模拟的不确定性。主要结论如下：

（1）从9 次试验模拟地表温度的月平均偏差来看，所有下垫面偏差中位数均小于0°C，模拟结果以负偏差为主。偏差的变化范围在7 月和8 月的模拟以及林地地区的模拟中较大，参数化方案的选择对模拟结果具有较大影响。

（2）方差分析表明物理过程敏感性受到季节和下垫面的影响，DVEG_CSR 过程在农田、林地、草地及春季和夏季灌木均通过敏感性检验的物理过程，对模拟影响显著，且大部分情况敏感性得分较高，是对地表温度模拟影响较大的物理过程。SFC过程在农田地区的春季是最敏感的物理过程，RAD 过程在林地的秋季与冬季对模拟影响最大。BTR 过程仅在农田地区的春季、夏季与秋季以及灌木地区的夏季模拟中表现出显著影响，且敏感性得分最低，相对于其他过程较不敏感。

（3）极差分析的结果表明，最优参数化方案组合同样受到季节和下垫面的影响，没有一种参数化方案组合在所有下垫面所有季节都表现最优。在对模拟有显著影响物理过程中，DVEG_CSR 的ON-Ball-Berry 的方案在春、夏、秋季模拟效果好，而冬季则是关闭动态植被与Ball-Berry 方案组合更佳；BTR 过程的Noah 方案与RAD 过程中GAPFVEG方案始终优于其他方案；SFC 显著性过程中在农田地区以M-O 方案模拟表现较好，其他下垫面则是Chen97 更优。

（4）偏差与无偏均方根误差误差分析结果表明，无论是从误差空间分布，还是误差时间变化分布上选用开启动态植被，CRS 过程的Ball-Berry 方案，BTR 过程的Noah 方案，SFC 的M-O 方案与RAD 过程的GAPFVEG 的参数化组合方案在东南区域的地表温度模拟中，站点的偏差绝对值与无偏均方根误差，相较于其它组合，表现出较低的水平，有较好的适用性。

上述研究表明，正交试验设计能够有效减少实验次数，在模式参数化方案寻优研究中有良好的优化试验的能力，从而能减少模拟的不确定性。由于最优参数化方案受下垫面类型和模拟季节的影响，且对于整个区域平均误差效应而言，实际上还受到不同类型下垫面面积的影响，因此，区域最优方案因地区而异（Li et al., 2019; Gan et al., 2019）。正交试验法作为优化试验方法，指标较单一，候选优化方案的确定存在一定不确定性，从而对实验结果带来影响，另外，仍需要结合模拟参数加强对优化参数化方案的理论物理过程和机理研究，以及多参数模拟的优化参数化方案研究。