政府奖惩下纺织品闭环供应链的优化策略研究
刘同超,尹巧娜
(许昌学院 商学院,河南 许昌 461000)
随着社会的发展和进步,服装更新换代速度大大加快,淘汰纺织品会造成环境污染,随着地缘政治经济局势紧张,纺织品原材料短缺和价格上涨,中国纺织业原材料依赖进口,且有效回收率严重不足,十分有必要对纺织品供应链进行优化升级。在需求增加和原料短缺的情况下,对回收资源进行充分的加工再利用,对缓解原材料危机、改善环境都有显著的效应[1]。
企业闭环供应链的研究一直是学者关注的重点,目前国内外关注的焦点主要集中在不同主体对再制造、供应链协调与定价、碳排放、博弈论等方面[2]。范定祥发现由线上和线下回收商、零售商、制造商组成的多回收主体模式可以使得供应链系统的整体利润达到最大[3]。丁斌把供应链的回收工作分为横向与纵向,发现横向可以提高回收数量,纵向可以提高回收质量[4]。卢茂盛考虑市场需求的不确定性,分析决策者的风险规避程度中性时,制造商和零售商都倾向于承担服务贸易[5]。孟丽君等讨论质量约束效应产生的影响,发现新制品和再制品在“质量水平—价格”维度存在差异,不对等的市场地位有利于产品质量水平的提高[6]。谬林发现随着回收率的提高,零售商的回收渠道要优于制造商的回收渠道[7]。莱萨尔(Lessard)等发现顾客的环保意识较低时,对回收价格更敏感,供应链也就更倾向于选择制造商、零售商和第三方的回收渠道[8]。
政府的奖惩作用也是供应链研究的重点。张晓青研究了在政府奖惩下,回收商主导的闭环供应链的定价策略,发现回收率奖惩和碳排放奖惩之间的相互作用可以影响到系统的决策[9]。王道平等在政府奖惩机制下,分析了由零售商主导的、制造商回收的闭环供应链的动态博弈策略,得出政府引导必要性的结论[10]。Himmel等人研究奖惩机制对于闭环供应链决策的影响并得出结论,RPM可以提高回收商的实际回收率和利润,高强度的奖惩强度可以促进环境发展的可持续性,充分体现政府作用的有效性[11]。王玉燕等考虑政府奖励机制的影响,对闭环供应链中的利他关切性决策进行研究,发现政府奖励强度的设置存在阈值,只有奖励强度大于阈值时,奖励机制才会生效[12]。姚锋敏等基于政府回收补贴和零售商企业社会责任投资,发现政府的回收补贴效果是显著的,可以降低产品价格,增加利润的同时提高零售商的企业社会责任投入水平[13]。代业明等结合碳税监管,讨论零售商的双重行为偏好对于成员定价决策的影响,发现征收碳税时,制造商和再制造商的联盟虽可以降低再制品价格,但不影响新产品定价[14]。
闭环供应链的应用方面。银新逸研究废旧快递纸箱的回收定价策略,分析由第三方单独回收和快递企业与第三方联合回收的情形,发现增加快递纸盒的重复利用率可以降低零售价格[15]。楼高翔发现与无补贴相比,回收量补贴政策下的回收率较大,按照回收电池容量补贴政策下的回收率可能较小[16]。焦建玲探讨了回收模式选择对于碳排放的影响,发现当再生材料收益到达某一阙值时,制造商作为回收主体的模式为最优[17]。孙嘉轶构建了回收商无资金约束的基准模型、资金约束回收商向制造商及电商平台融资的决策模型,求解电商闭环供应链的最优回收和定价决策[18]。李文川等把灾害传播动力学与闭环供应链相结合,构建闭环供应链风险传播模型,发现控制风险蔓延只有在风险阈值系数超过临界风险阈值系数时才会有效,制造商作为中心节点,遇到风险时所产生的影响也更大[19]。
现阶段大多数的闭环供应链研究,较少涉及实证研究,特别是对于纺织品的闭环供应链研究较少涉及。同时,针对政府奖惩机制下结合纺织品回收方式和回收特点的研究较少。本文运用顾客的保留价格衡量市场的需求函数,研究纺织品行业闭环供应链系统中分别由制造商、零售商、第三方回收的最优定价和产量策略,并提出收益共享契约模型进行优化,并对纺织品的回收方式过程中的关键问题进行分析,提出促进纺织品闭环供应链发展的一些措施。
一、基本假定和模型符号描述说明
(一)基本假定
1.假定供应链中各决策成员均为理性的“经济人”,其目标都为自身利益最大化。
2.假定制造商生产的新产品和再制品具有质量差别,且消费者可以辨别区分。
3.假定废品回收量为市场对再制纺织品的需求量q2,且q2=n2q1。
4.假定制造商、零售商、顾客之间的对于纺织品的需求量相同,不存在库存积压、物料折损等意外情况,供给量即为需求量。
5.假定第三方回收中心对从消费者处回收的废旧纺织品有三个流向:a.无偿捐赠给贫穷国家或地区,作为福利支出;b.出售给有能力专业处理各式废旧纺织品的回收商;c.直接就地掩埋或焚烧,作为垃圾处理。三个流向当中,废旧纺织品所占比例分别为n1、n2、n3,且n1+n2+n3=1。
(二)模型符号描述
新纺织产品的市场预计需求q1;
再制纺织品的市场预计需求q2;
制造商制定新纺织产品的批发价格p1;
制造商制定再制纺织品的批发价格p2;
零售商制定新纺织产品的销售价格l1;
零售商制定再制纺织品的销售价格l2;
回收方对消费者开出的废旧纺织品的收购价格pr;
回收方回收的用于再利用的回收量为qr,包括无偿福利捐赠和再制品的回收利用;
制造商生产单位新纺织产品的成本c1(包括新制品原料价格、生产成本);
制造商生产单位再制纺织品的成本c2(包括再制品原料价格、生产成本);
假定制造商、零售商和第三方负责回收处理废旧纺织品的单位成本都为cr(包括运输成本和再处理成本);
假定回收成本低于再制造纺织品的成本,即cr 假定政府对于回收者的奖惩为k。假定回收率为n2,政府规定回收率为b,当n2>b时,政府对回收中心每单位回收产品实行奖励k=k1≥0,当n2 假定顾客对于产品的估价是一个服从参数为λ的指数分布,市场对于纺织品的需求量是关于产品价格、心理估价、顾客到店率的服从λ1泊松分布的函数。 若顾客对产品的心理预期价格为P,则衡量顾客对产品心理预期的概率密度函数和累积分布函数分别是f(P)和F(P),F(P)描述的是顾客对于产品的心理预期小于产品销售价格的概率。当顾客对于产品的心理预期价格高于产品销售价格时,顾客将愿意购买,1-F(P)则是描述顾客购买产品的概率[20]。 假定用纺织品市场需求量的期望值直接代替市场中的需求量Q,则Q=λae-λP,λa为单位时间内顾客的到达人数。 政府为了降低碳排放量,早日实现“碳达峰”和“碳中和”,对制造商、零售商、第三方实行奖惩机制,以促进废旧纺织品闭环供应链的形成。对不合作的纺织品制造商实行惩罚机制,强制征收税费;对回收方实行奖励机制,超过政府制定的回收率标准,每单位实行奖励机制。在此机制下,政府可以有效地提高各供应链成员的积极性,以达到降低资源浪费和保护环境的目的。 本阶段运用博弈论的方法研究在政府惩罚机制之下通过经济效益将制造商、零售商以及第三方形成闭环供应链模型,研究包括制造商、零售商、顾客和第三方,在政府的奖励下,通过构造闭环供应链的需求函数,运用斯塔克伯格模型求解出最优的选择策略。 1.制造商负责纺织品回收的合作闭环博弈模型 在此模式下,制造商积极响应国家政策,不仅售卖再制品,而且主动参与回收业务,形成由制造商、零售商、顾客三方的闭环供应链。 制造商参与政府绿色物流政策,予以补贴,不征收碳排放量税费且参与回收,政府视情况予以奖惩。该模式是由制造商直接回收再制造废旧纺织品。 新制造的纺织品市场需求量为q1,再制造的纺织品的市场需求量为q2。 q1=λae-λl1,q2=λae-λl2,且q2=n2q1 (1) 零售商利润函数为: πl=(l1-p1)q1+(l2-p2)q2 (2) 对l1求偏导数,令∂πl/∂l1=0得: (3) 对l2求偏导数,令∂πl/∂l2=0得: (4) 若n2≥b,则政府对回收方实行奖励机制,每单位回收产品实行奖励为k,此时k=k1≥0,则制造商的利润函数为: πz=(p1-c1)q1+(p2-c2+k1)q2-crqr (5) 其中q1=λae-1-λp1,q2=λae-1-λp2,qr=n2q1 对p1求偏导数得,令∂πz/∂p1=0得: (6) 对p2求偏导数得,令∂πz/∂p2=0得: (7) 若n2 由制造商负责废旧纺织产品的闭环供应链的利润为: π=πz+πl=(p1-c1)q1+(p2-c2+k2)q2-crqr+(l1-p1)q1+(l2-p2)q2 (8) 将p1、q1、p2、q2、l1、l2带入上述函数当中,得: (9) 2.第三方负责回收纺织品回收的合作闭环博弈模型 该模式是指制造商与第三方签订订购合约,从第三方回收中心购买处理之后的纺织品原材料。这种模式可以减轻生产能力较小的制造商的生存压力,减少物流投资和简化风险,使其聚焦于自己的核心业务。 假定第三方回收中心是一个完全的“经济人”,仅考虑自己的收益率,对废旧纺织品再制原料的出售价格由总成本决定,再利用一定的预期收益率来决定价格。在此博弈模型当中,制造商是斯塔克伯格博弈当中的价格领导者,采用逆向求解法。 假定预期利润率为i,第三方回收中心对废旧纺织品再制原料的预期价格pc=cr(1+i),当面临政府奖惩的时候,第三方为了自己的利润不受损失,一定会将政府的奖惩转移给制造商,则再制品原料的出售价格为pr=cr(1+i)-k。 当n2>b时,政府对回收中心每单位回收产品实行奖励k=k1≥0;当n2 则新制纺织品和再制纺织品的市场需求函数对零售商需求利润函数为: πl=(l1-p1)λae-λl1+(l2-p2)λae-λl2 (10) 对l1求偏导数,令∂πl/∂l1=0 得: (11) 对l2求偏导数,令∂πl/∂l2=0得: (12) 将零售商制定的新制纺织品和再制纺织品的销售价格带入市场需求函数当中,求得q1=λae-1-λp1q2=λae-1-λp2 制造商利润函数为: πz=(p1-c1)q1+(p2-c2-pr)q2 (13) 对p1求偏导数得,令∂πz/∂p1=0得: (14) 对p2求偏导数得,令∂πz/∂p2=0得: (15) 在第三方预期利润率为i的情况下,政府对第三方回收中心的奖惩约束直接与第三方的利润有关,作为一个完全理性的第三方永远追求自身利润最大化,必然会尽力收集废旧纺织品完成政府任务量,即第三方的利润为: πd=icrq2πd=icrλae-1-λp2 (16) 由第三方单独负责废旧纺织产品回收的闭环供应链整体利润为: π=πz+πl+πd=(p1-c1)q1+(p2-c2)q2-prq2+(l1-p1)q1+(l2-p2)q2+icrq2 (17) (18) 3.零售商负责纺织品回收的合作闭环博弈模型 该模式中零售商参与废旧纺织品的回收,零售商既制定给顾客的销售价格,又参与回收,影响制造商的回收原料成本。因为零售商作为制造商和顾客的中间方,既与制造商有着密切的联系,又与顾客之间关系密切,所以零售商直接参与回收废旧纺织品要比其他成员参与回收更有便利性,在正向物流当中,制造商把纺织品批发给零售商,零售商对顾客进行销售;在逆向物流当中,制造商委托零售商进行回收废旧纺织品,这两个的物流方向都是由制造商主导的斯塔克伯格博弈模型。 图3 零售商负责回收模型图 此模式下,制造商参与政府绿色物流政策,予以补贴,不征收碳排放量税费;零售商参与回收,若达到回收率,则政府每单位予以k1的补贴。 零售商的利润函数为: πl=(l1-p1)λae-λl1+(l2-p2)λae-λl2+(pr-cr)λae-λl2 (19) 对l1求偏导数,令∂πl/∂l1=0得: (20) 对l2求偏导数,令∂πl/∂l2=0得: (21) 制造商的利润函数为: πz=(p1-c1)q1+(p2-c2-pr)q2=(p1-c1)λae-1-λp1+(p2-c2-pr)λae-1-λ(p2-pr+cr) (22) 对p1求偏导数得,令∂πz/∂p1=0得: (23) 对p2求偏导数得,令∂πz/∂p2=0得: (24) 零售商负责旧衣纺织产品的回收的闭环供应链整体利润为: π=πz+πl=(p1-c1)q1+(p2-c2-pr)q2+ (l1-p1)q1+(l2-p2)q2+(pr-cr)qr (25) (26) 通过对不同模式下纺织品回收的合作闭环博弈模型分析,可以得出利润不同(表1)。对比分析三个闭环供应链模型可得,由制造商负责回收的闭环供应链模型要优于由零售商负责回收的闭环供应链模型。由第三方负责回收和由制造商负责回收的闭环供应链模型的利润大小取决于它们参数i和k的大小,需要根据具体情况进行分析。 表1 三个模型的整体利润 在政府的激励之下,全体成员都会尽可能地争取政府的补贴,以降低成本提高收益。此时问题为如何提高回收率,以达到政府要求标准。即问题转化为如何设计出更合理的闭环回收模式,降低再制纺织品的零售价格。为提高供应链整体利润,使模型更贴近现实,实现帕累托改进,提出收益共享契约模型。 此模型是制造商为了零售商增加订购量、刺激销售和提高总收益的一种协调方式。通过此模式零售商可以得到制造商的批发价格,进而可以制定一个较低的零售价格,从而提高销售量;通过此模式制造商的利润直接与零售商销售数量有关,与零售商利润直接联系。零售商和制造商的紧密联系一定会提高供应链系统的稳定性,提高抵御风险能力。 制造商负责废旧纺织品的回收,给零售商一个较低的批发价格,为简便处理,假定批发价格为制造商的生产成本,获得一部分零售商的销售收入收益,以刺激零售商增加订货量。 假定制造商所占的收益共享比例为α,那么零售商所占的收益共享比例自然为1-α。考虑整体利润最大化,k=k1≥0,为政府奖励。 制造商的利润函数: πz=(p1-c1)q1+(αl2-c2+k1-cr)q2 (27) 零售商的利润函数: πl=(l1-p1)q1+(1-α)l2q2 (28) 闭环供应链系统的利润函数: π=πz+πl=(l1-c1)q1+(l2-c2+k1-cr)q2 (29) 对l2求偏导数,令∂πl/∂l2=0得: (30) 第三方负责废旧纺织品的回收,按照预期利润率,制定对废旧纺织品再制原料的出售价格,制造商一个较低的批发价格,为简便处理,假定批发价格为再制造纺织原料成本的价格给制造商,获得制造商的销售收益。假定收益共享比例为α,假定第三方为外生变量。 制造商的利润函数: πz=(p1-c1)q1+αl2q2 (31) 零售商的利润函数: πl=(l1-p1)q1+((1-α)l2-c2-pr)q2 (32) 第三方的利润函数: πd=icrq2 (33) 不考虑第三方的闭环供应链系统的利润函数: π=πz+πl=(p1-c1)q1+αl2q2+ (l1-p1)q1+((1-α)l2-c2-pr)q2 (34) 对l2求偏导数,令∂πl/∂l2=0得: (35) pr=cr(1+i)-k1是由第三方所决定的,是一个外生变量。 表2 两模型再制品零售价格比较 结论3:由第三方负责回收的供应链收益共享契约模型零售价比由制造商负责回收的供应链收益共享契约模型零售价更低,模型得到了优化,实现帕累托改进。事实上,制造商作为整个系统当中的主导者,应该制定行之有效的协调契约合同,提高供应链各方的利润,使各方得利。 利用数值验证上述结论的正确性,首先模拟参数λ变化对于模型所产生的影响,其次模拟再制品回收成本变化对于模型产生的影响,最后分析收益共享模型因再制品价格降低、产量提高所带来的帕累托改进。为简便计算,假定单位时间内顾客到达人数λa=1000,制造商生产单位新纺织品的成本c1=30,生产再制纺织品成本c2=32,各方回收纺织品成本cr=10,第三方的预期利润率为10%,政府的奖惩都为3,即k1=3,k2=-3,假定λ∈[0.01,0.05][20],每次间隔0.01。选择政府奖惩下闭环供应链模型模拟参数变化对于价格、产量、利润、回收率的影响。 表3 不同回收模式时参数变化情况 结论1:从表3中可以充分看出,参数λ越小,新制品和再制品的预期价格越高,市场需求越高,预期的整体利润也越高,回收率也越高。参数λ与价格、产量、利润、回收率均成反比。参数λ的大小与顾客对产品的满意程度有关,如产品的重要性、产品的用途多少、产品的耐用性等,是顾客根据产品性能而产生的主观上的倾向。 结论2:除了λ的取值发生变化,其他参数不变时,可以明显看出由制造商回收的利润最高,由第三方负责回收的利润稍次之,零售商负责回收的利润较小,而制造商拒绝回收的利润最小。所以理性的制造商一定会按照政府的意愿,进行再制品的销售,从而形成闭环供应链。 结论3:对比由制造商回收和由零售商回收两种情况,两者的回收率相同而利润不同,说明由制造商负责回收的情况要优于由零售商回收。究其原因是因为由制造商回收时不涉及再制纺织品原料的出售,制造商把废旧纺织品回收处理成原料,可以直接把原料加工成纺织品。 结论4:由第三方负责回收的利润不仅与第三方的预期利润率i有关,而且与第三方的回收成本也有着很大的关系。此模型假定i=10%,但第三方假定的预期利润率越高,其利润也就越高,利润率的大小根据市场行情而定,作为投资依据。同样,第三方的回收成本越小,其利润也会越高,第三方回收才会相比制造商回收更具有优势。 政府奖惩的大小直接与产品的成本相关,政府通过影响产品回收成本对产品的定价、产量、回收率产生影响,进而影响厂商利润,迫使厂商按照政府意愿组织生产。 由制造商负责回收纺织品时,政府的奖惩程度与供应链整体利润成负相关,政府的惩罚力度越大,整体利润越高,制造商把惩罚转移给零售商,零售商再转移给顾客,进而导致零售价增高,而回收率降低。针对于此,政府一味地加强惩罚力度的做法是不可取的,反而应该鼓励制造商参与回收,提高奖励力度,增加回量。 表4 不同回收模式时奖惩变动情况 第三方回收利润与政府的奖励程度成正相关,奖励程度越大,零售价越低,整体利润高,回收率也越高。政府应加大奖励,当零售商参与回收时,整体利润是不发生改变的,但是政府奖励越高,再制品零售价降低,对再制品的需求量也提高,回收率也增大。说明由零售商参与回收可以很好地将政府的奖惩转移到消费者的购买力度方面,而不影响整体利润的大小。 假定单位时间内顾客到达人数λa=1000,制造商生产单位新纺织品的成本c1=30,生产再制纺织品成本c2=32,无论制造商还是第三方回收成本cr=10,λ=0.03。 与原先模型相比,两模型收益共享之后,再制品零售价都下降,产量提高,利润提高,得到了帕累托改进。但是第三方参与回收的收益共享之后获得的整体利润要小。本文中假定第三方回收与制造商回收的再处理成本是相同的,如果第三方的回收成本可以低于制造商回收成本,那么第三方的存在就有一定的必要性。相反,如果第三方的回收成本大于制造商的回收成本,那么第三方就没有存在的必要性。 表5 不同回收模式的收益共享情况 从图4可以看出当第三方回收纺织品而没有成本优势时,制造商负责回收废旧纺织品时的利润是要优于第三方的。第三方存在的前提在于第三方的回收较制造商来说具有技术优势,可以降低回收成本。 图4 第三方成本变动的利润变化 本文分析了政府奖惩下废旧纺织品闭环供应链的定价策略影响,提出了收益共享契约模型,最后得出结论:第一,收益共享契约模型使得收益得到优化,废旧纺织品回收率得到提高;第二,回收率与再制纺织品的零售价格密切相关,零售价又与成本密切相关,提高利润的根本方法唯有创新以降低成本;第三,如果第三方回收成本较低,其利润将会提高,第三方之所以存在是因为回收成本低,如果第三方回收成本高,则第三方回收不存在。 根据本文结论,提出以下对策。 第一,降低生产成本。生产价格的高低直接影响了企业利润的多少,只有降低成本才有降低价格的可能。因此,企业应该激发内生动力,积极投入研发,提高自身能力,降低生产成本,以利于提升纺织品回收的经济效益,促进废旧纺织品闭环供应链的发展。 第二,重点发挥政府作用。据本文当研究,政府的作用是显而易见的,运用奖惩机制,可以有效激励各个成员加入到废旧纺织品再利用的过程中,增加供应链的总利益,增进社会总福利,提高民众生活水平,获得更高的经济效益和更好的社会效益。废旧纺织品闭环供应链的形成需要政府的积极参与,形成切实有效的规章制度,加大鼓励第三方进入市场,在市场机制失灵的时候,充分发挥政府的调节机制,成为市场“看得见的手”。(三)市场预计需求函数
二、政府奖惩下闭环供应链定价策略
(一)闭环供应链博弈模型
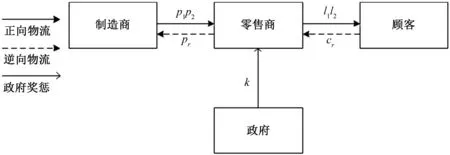
(二)闭环供应链利润比较分析

三、政府奖惩下闭环供应链定价策略的优化研究
(一)由制造商负责回收的供应链收益共享契约模型
(二)由第三方负责回收的供应链收益共享契约模型

(三)模型对比分析的结论
四、数值实验及分析
(一)参数灵敏度分析

(二)政府奖惩度分析

(三)收益共享模型优化

(四)第三方成本变化分析
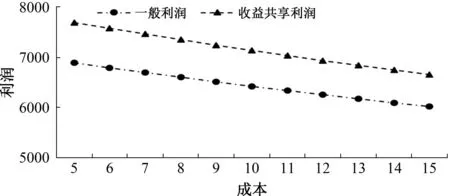
五、结论与对策

