相变填充床储热系统研究与应用进展
张岩岩,熊亚选,陈亚辉,全瑞星,程广贵,赵彦琦,3,丁玉龙
(1江苏大学机械工程学院,江苏 镇江 212013;2北京建筑大学环境与能源工程学院,北京 100044;3航空飞行器热管理与能量利用工业和信息化部重点实验室,江苏 南京 210016;4伯明翰大学化工学院储能研究中心,英国 伯明翰 B15 2TT)
当前全球能源供需面临巨大挑战,碳中和目标推动了能源结构的改变,可再生能源和余热能源利用占比日益增多[1]。然而,当利用太阳能、风能、余热等能源时,它们的瞬时性及间歇性的缺点限制了其稳定有效的能量输出[2],有必要发展储能技术以解决供给与需求之间的矛盾以及提升能源利用效率。全球90%的能量转换、传输、存储基于热能形式,并且全球50%以上能量终端需求为热能[3-5],因此,热能脱碳对于实现碳中和具有重要意义,而储热技术因储能密度高、循环寿命长、储能规模大、可集成度高、热利用效率高等优点[6],可有效提升热能利用效率,在近年来拥有极高的科研热度。如图1所示,储热技术的相关论文发表数逐年增加,2020 年相比2018 年论文增量最多达到了220 篇,2020—2022 年论文增量有所减少,但也增加了103篇。
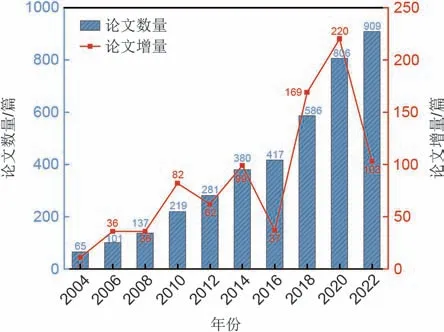
图1 储热技术相关论文统计(数据来源:中国知网)Fig.1 Statistics of papers related to heat storage technology (source: China National Knowledge Infrastructure)
填充床具有结构紧凑、换热效率高、储能密度高等优点,已被广泛应用于化工过程、热能存储等领域[7]。如图2 所示,填充床储热系统外壁为隔热层,内部放置具有合适尺寸的颗粒或其他形式固体的储热介质,以实现高储能密度热能存储。填充床下部有筛网以支撑储热介质,传热流体在填充床内流动,与储热介质表面接触以实现储热系统的储热与释热。填充床储热系统主要基于三种储热方式:显热储热、相变储热和热化学储热[8]。显热填充床储热系统具有低成本特征,然而因显热材料自身能量密度相对较低,在大规模应用中具有建造环境、后期维护方面的挑战。热化学填充床储热系统具有极高的储能密度,然而现有研究表明该系统的循环寿命较低,因此仍处于概念验证阶段[9]。相变填充床储热系统具有较高的储能密度、稳定的循环性能与长循环寿命,并且相变材料固有的相变特征,具有稳定的温度控制能力。因此,相变储热填充床是一种理想的热能储存解决方案,它能够实现高效的能量储存和释放,满足不同应用场景的能源需求。本文针对相变填充床储热系统,在第一部分介绍了相变填充床储热系统的数值模型,包括舒曼模型、单相模型、连续固相模型、混合扩散模型。第二部分介绍了相变填充床储热系统性能评估方法,包括能量效率分析,㶲效率分析。第三部分介绍了填充床储热系统的优化设计,包括储罐的结构设计,传热流体的选择,储热单元的封装方法。最后,从工业余热回收、太阳能热能收集等方面总结了相变填充床储热系统的应用情况。

图2 相变填充床结构[10]Fig.2 Packed-bed latent thermal energy storage structure[10]
1 数值模型
对于相变填充床储热系统,蓄放热本质是传热流体和相变材料胶囊在填充床内部的对流传热。由于相变填充床储热系统的高实验成本以及复杂的瞬态性质[11],因此研究人员开发出几种不同的相变填充床储热系统数值模型。这些数值模型主要用于预测相变填充床储热系统的蓄放热过程[11]。根据在蓄放热过程中,液相和固相温度是否相同,这些数值模型可以分为两类:单相模型、两相模型,其中两相模型包括舒曼模型、连续固相模型和混合扩散模型。
1.1 舒曼模型
舒曼模型[12]是一种基于多孔介质模型假设的非热平衡两相传热模型,主要包含两个方程,分别描述传热流体(液相)和多孔介质相变填充床(固相)的能量守恒[13]。该模型既不考虑流体中的传导,也不考虑固相中的传导,大大简化了求解的复杂性[14],因此舒曼模型的计算量较小,但反映流体温度分布和反映填充床温度分布的准确性较低。
对于传热流体:
其中ε是填充床孔隙率,ρf是传热流体密度,Cpf是传热流体比热容,Tf是传热流体温度,Ts是固体材料温度,h是传热流体和固体颗粒之间的传热系数,as是每单位床体积的表观颗粒面积。
对于固体材料:
其中ε是填充床孔隙率,ρs是固体材料密度,Cps是传热流体比热容,Tf是传热流体温度,Ts是固体材料温度,h是传热流体和固体颗粒之间的传热系数,as是单位床体积的表观颗粒面积。
as可以由以下表达式确定:
ε是填充床孔隙率,d是固体颗粒直径。
1.2 单相模型
单相模型由Vortmeyer 和Schaefer[15]在舒曼模型的基础上改进,用单一方程模拟填充床,计算的温度是固相的温度[16]。单相模型忽略了传热流体和相变材料之间的热传递,认为传热流体和相变材料的瞬时温度相等[17]。单相模型适用于高热导率相变材料,因此对于石蜡、脂肪酸和大多数水合盐不适用,但适用于高热导率高温填充床相变储能系统[14]。
单相模型的能量平衡通常写为:
其中ε是填充床孔隙率,ρs是固体填充材料密度,Cps是固体填充材料比热容,T是固相和流体相瞬时温度,ṁf是流体质量流量,Cpf是传热流体比热容,λax是填充床床轴向有效热导率。
λax计算公式如下:
其中0.7<δ<0.8,Re表示雷诺数,Pr表示普朗特数,λf表示传热流体导热系数
1.3 连续固相模型
连续固相模型基于集总参数法,将填充床系统视为具有均匀固体温度和不同流体温度的连续多孔介质。连续固相模型考虑了轴向和径向热传导,可以分析充放热过程中径向热梯度的影响,这对于研究热损失大或入口流量分布不均匀的相变填充床储热系统具有重要意义。
相变材料和传热流体上的能量平衡方程可写成:
其中Tf是传热流体温度,Tp是相变材料温度,u是传热流体平均速度,ε是填充床孔隙率,ap是每体积球形胶囊表面积,heff是相变材料和传热流体之间的有效传热系数。
液相阶段(第一阶段):
其中ρl是相变材料液相阶段密度,cl是相变材料液相阶段比热容,ε是填充床孔隙率,Tp是相变材料温度,Tf是传热流体温度,ap是每体积球形胶囊表面积,heff是相变材料和传热流体之间的有效传热系数。
凝固阶段(第二阶段):
其中L是凝固相变潜热,β是固相分数,Tm是凝固温度。
固相阶段(最后阶段):
其中ρs是相变材料固相阶段密度,cs是相变材料固相阶段比热容,ε是填充床孔隙率,Tp是相变材料的温度,Tf是传热流体温度,ap是每体积球形胶囊表面积,heff是相变材料和传热流体之间的有效传热系数。
其中Nu、Re、Pr分别为传热流体的努塞尔数、雷诺数和普朗特数。
Ms和Mc是固化的相变材料和胶囊盖的热阻与胶囊外表面对流引起的热阻之比。
1.4 混合扩散模型
Ismail 和Henriquez[18]提出的混合扩散模型将填充床视为由许多各向同性球形胶囊组成的多孔介质。混合扩散模型与舒曼模型的区别在于在两组能量方程右侧增加了轴向热导率项。圆柱形储罐在轴向上被分成几个微层,其中流体温度被认为是均匀的。该模型将相变材料和传热流体之间的传热分解为两个阶段:胶囊外对流传热和胶囊内热传导。混合扩散模型的关键是考虑相变材料胶囊内部的热梯度。
相比于上述三种模型,混合扩散模型可更准确地反映出填充床储热的瞬态热行为。然而,由于需要计算在不同位置具有代表性的填充物内部温度分布,该模型的计算量远大于上述三者[16]。
修正后瞬态一维混合扩散模型的控制方程如下[19]。
传热流体质量守恒方程:

其中Tl为熔盐温度,(Tp)R为相变材料胶囊表面温度,cp,l为熔盐比热容,Γl,eff为熔盐有效热导率,右侧最后一项为熔盐与相变材料胶囊之间的传热,其体积间隙传热系数为hv。
相变材料胶囊的能量守恒方程:
其中ξ为每个胶囊内部的径向坐标,hp为相变材料焓值,ρp和kp分别为相变材料的密度和导热系数。
填充床填充层的惯性系数和渗透率可表示为[20]:
其中dp是球形胶囊直径。
传热流体和相变材料胶囊之间的间隙传热系数hv和传热流体有效热导率Γl,eff,给出为[21]:
其中普朗特数和雷诺数表示如下:
当相变材料处于液相时,可能存在增强传热的自然对流。采用以下液体相变材料的有效热导率来说明自然对流效应[22]:
Ra、v、α、β分别是瑞利数、液态相变材料的运动黏度、热扩散系数和热膨胀系数。
2 相变填充床储热系统性能评估
2.1 能量效率分析
为了获得相变填充床储热系统的能量存储性能,需要对能量效率进行评估[23]。能量效率分析基于热力学第一定律的能量守恒原理[24],能量效率指储热系统释热与储热能量之间的比率[24]。
其中Q̇total是传热流体传递到相变材料的传热率,Q̇PCM是相变材料储热率,Q̇loss是储热单元向外界环境的散热率。
其中Cp,f是传热流体比热容,ṁf是传热流体质量流量,Tf,in是传热流体温度,Tf,out是出口传热流体温度。
其中Qtotal是传热流体传递到相变材料的累计传热量,Q̇total是由传热流体传递到相变材料的传热率。
其中QPCM是相变材料累计储热量,mPCM是相变材料质量,TPCM是t时刻相变材料温度,TPCM,initial初始时刻相变材料温度,h是相变材料比热焓。
其中Q̇PCM是相变材料储热率,QPCM是相变材料累计储热量。
其中η1是能量效率,QPCM是相变材料累计储热量,Qtotal是传热流体传递到相变材料的累计传热量。
研究者对各种应用中的填充床结构、几何形状、运行参数与能量效率的关系进行了大量数值和实验研究。能量效率与罐体高度有关,Yang等[25]利用一个双温度模型来研究熔盐温跃层储热系统的温度分布和放热效率,发现无量纲储罐高度在10~800范围内,相变填充床效率随着储罐高度的增加而增加。然而,作者同时也发现,在雷诺数1~50范围内,效率随着雷诺数的增加而降低。入口温度和入口质量流量也会影响能量效率,Guo等[26]通过实验研究了相变填充床储热系统入口温度和入口质量流量对其热性能的影响,建立一维混合扩散模型模拟了填充床储热系统内部的传热过程,并将数值模型推广为无量纲模型,发现当Pe数从188 增加到338 时,热效率从65.6%提高到80.1%;当Ste数从0.479 增加到0.799 时,热效率从59.2%提高到77.6%。在储热材料特征与能量效率的关系研究中,Yang 等[25]发现使用较小的填料颗粒可以大大提高放热效率,5 cm 粒径比10 cm 粒径放热效率高出12.9%。储热层设计同样会对系统能量效率造成影响。Liu 等[27]提出了一种具有三层相变材料和三层直径胶囊的三维填充床储热罐模型,并通过数值模拟研究了其储能行为和热分层性能。结果表明,与传统的非梯级单层直径胶囊填充床储热罐相比,梯级三层直径胶囊填充床储热罐的储热热效率从24%提高到61%。Guo 等[28]发现合理的储热材料体积比可以提升梯级填充床储热系统热效率。作者构建了基于3∶6∶1体积比的苯二酚胶囊、己二酸胶囊和赤藓糖醇胶囊相变填充床,提升热效率至该系统最高值76.1%。运行模式同样会对能量效率产生影响。Schwarzmayr等[29]对填充床储热系统在待机模式下的待机效率(填充床储热系统的静态运行)进行了实验研究,着重探讨了在储热期间传热流体不同流动方向对填充床待机效率的影响。结果表明,在长待机时间内,传热流体流动方向对待机效率有显著影响。在反向流动过程中,能量效率高出5%。在对填充床结构设计对能量效率的影响中,Xie 等[30]研究了壁面对填充床储热系统热效率的影响,比较了钢壁高温中试规模储罐与聚碳酸酯壁低温实验室规模储罐,并均采用矿棉隔热。结果表明,储罐罐体内储存的能量对填充床放热过程具有负面影响,在填充床储热完全结束后,储罐罐体储存能量达到储存总能量的10%,这导致在填充床放热过程中温跃层厚度增加了15%。
2.2 㶲效率分析
㶲分析基于热力学第二定律,为从储热系统释放与充入㶲的比率[23]。
其中Ėxtotal是传热流体传递到相变材料的㶲传递率,ĖxPCM是相变材料的㶲存储率,Ėxloss是储热单元向外界环境的散热引起的㶲散失率,İ是㶲损率。
其中Ėxtotal是传热流体传递到相变材料的㶲传递率,ṁf是传热流体质量流量,Cp,f是传热流体比热容,Tf,in是进口传热流体温度,Tf,out是出口传热流体温度,T0是环境温度。
其中Extotal是传热流体传递到相变材料的累计㶲传递量,Ėxtotal是传热流体传递到相变材料的㶲传递率。
其中ĖxPCM是相变材料中热量㶲的存储率,Q̇PCM是相变材料的储热率,T0是环境温度,TPCM是t时刻相变材料温度。
其中ExPCM是相变材料中累计存储的热量㶲,ĖxPCM是相变材料中热量㶲的存储率。
其中η2是㶲存储效率,ExPCM是相变材料中累计存储的热量㶲,Extotal是传热流体传递到相变材料的累计㶲传递量。
根据公式(32)可知,能量效率只考虑到能量的转化和利用情况,它只对相变填充床储热系统的运行和性能进行简单的能量平衡分析。根据公式(38)可知,ExPCM表示相变材料中累计储存的热量㶲,即相变填充床储热系统产生的有用功,Extotal表示传热流体传递到相变材料的累计㶲传递量,即外部供给相变填充床储热系统的可用能量。最后通过整体㶲效率公式可知,㶲效率是指在一个系统中,有多少㶲被转化为有用的输出㶲。由此可知,㶲效率分析考虑了能量的品质和可用性,是能量效率分析的进一步扩展。
与对能量效率的影响类似,入口质量流量会对㶲效率产生影响,Wang 等[31]研究了与太阳能抛物面槽式集热器集成的相变填充床储热系统动态热性能,结果表明,稳态和非稳态入口边界条件在热性能方面存在显著差异。在稳态入口温度条件下,㶲效率随着质量流量的增加而逐渐降低。在入口温度不稳定的情况下,质量流量对㶲效率影响不大,约为41.00%。在针对相变填充床储热系统储热层研究中,Cárdenas 等[32]全面讨论了颗粒尺寸、长径比和储热材料质量对填充床在整个工作周期中的㶲损失的影响,结果表明,当填充床储热材料质量多出50%、长径比为0.6 和粒径为3.7 mm 时,为最佳配置,具有98.24%的往返㶲效率。在储热单元特征、工作参数与㶲效率的研究中,Sun 等[33]在舒曼模型基础上,建立了一维双能方程两相填充床储能装置数学模型,分析了球形储热单元相变填充床储热特性,发现减小球形储热单元直径可以提高相变填充床㶲效率。同时作者发现,雷诺数和Stefan数的增加也可以提高相变填充床㶲效率。储热单位的布置方位会影响系统㶲效率。Kumar等[34]采用焓-孔隙率技术和非平衡能量方程建立了传热流体、相变材料和储罐壁面的数值模型,来研究圆柱形储热单元相变填充床储热特性,发现与横向布置的圆柱形储热单元相比,轴向布置的圆柱形储热单元具有更好的㶲效率。储热层梯级设计同样会对系统㶲效率造成影响,Gao等[35]为太阳能供暖系统设计了一个梯级相变填充床储热系统,并且建立了基于热阻分析的一维两相模型,并通过不同实验验证模型适应性。结果表明,在相同操作条件下,梯级填充床热能储存比单级热能储存具有更均匀的温度分布,而均匀的温度分布是提高㶲效率的关键因素,最终储热完成后㶲效率提高了5%。Zhu等[36]利用相变填充床循环热性能模型分别对单级相变填充床、两级相变填充床、三级相变填充床进行了数值模拟,发现采用不同粒径的梯级相变填充床具有更高㶲效率,对于两级相变填充床来说,当上层粒径为0.025 m,下层粒径为0.035 m时,㶲效率最大;对于三级相变填充床来说,当上层粒径为0.025 m,中层粒径为0.0325 m,下层粒径为0.00325 m时,㶲效率最大。
3 相变填充床储热系统
3.1 储罐设计
填充床储热系统储罐的设计直接影响余热回收系统的成本和效率。表1对部分储罐几何形状优化设计工作进行了总结,目前储罐形状一般为圆柱形,也存在矩形[37]和截锥形[38]。

表1 储罐几何形状的优化设计Table 1 Optimal design of storage tank geometry
圆柱形储罐具有机械应力更低、稳定性更好的优点。并且由于没有拐角效应,传热流体流动更加均匀[14]。Cárdenas等[32]通过调整填充床纵横比,可以实现填充床性能提升,在其他参数相同的情况下,填充床的㶲效率随着纵横比α的降低而增加,直到达到0.5<α<0.8 之间的最大值后,低于该值后,填充床的㶲效率再次降低。Zanganeh 等[38]研究了截锥形填充床,如图3 所示,储罐浸没在地下,其截锥形状可以减小储罐由于岩石热膨胀引起的热棘轮效应,并且降低填充床顶部热损失。Li等[37]建立了基于碳酸盐相变材料砖的矩形床结构,如图4所示,在填充床内使用复合相变材料砖布置出曲折流通通道,增大了传热表面,强化了传热湍流。

图3 中试规模储热配置和实验设置方案,截锥形储罐浸没在地下,热电偶位于填充床内部不同的垂直位置[38](单位:mm)Fig.3 Scheme of the pilot-scale thermal storage configuration and experimental setup, truncated cone shape is immersed in the ground with thermocouples at different vertical positions inside the packed bed[38] (unit: mm)

图4 基于定型复合相变材料填充床储热系统的示意图 (a) 三维视图;(b) 横截面视图;(c) 和 (d) 几何尺寸[37](单位:mm)Fig.4 Schematic illustrations of the composite phase change materials based packed bed thermal energy storage system (a) 3D view; (b) cross-section view; (c) and (d) geometrical dimensions[37] (unit: mm)
储罐隔热设计对于减少热量损失也至关重要[14]。Yang 等[39]利用综合传热计算模型比较了绝热和非绝热边界对熔盐填充床性能的影响,发现非绝热边界下的热损失扭曲了熔盐填充床温度分布和传热流体分布,同时作者发现当雷诺数超过250时绝热和非绝热边界的熔盐填充床释热效率基本一致。Xu等[20]开发了二维两相模型,其中包含隔热和储罐壁面的能量方程。结果表明,即使壁面附近的传热流体温度受到壁面温度的轻微影响,通过增加隔热层厚度也可以在横截面上形成均匀温度分布。
流道设计对填充床储热性能影响很大。Vannerem等[40]基于容量为107 kWh 的相变填充床实验研究了流体分布对填充床储热系统储存的影响。通过对比均匀型、中心型、外围型三种分流器,发现均匀型分流器径向温度分布最均匀。Bellenot 等[43]为了研究流体分布对双介质填充床储热性能的影响,建立了一个数值模型。但该模型仍需要一些实验验证对比,预计它将有助于研究装有分配装置的填充床储热性能,该分配装置用于实现传热流体的均匀流动。Lou等[44]通过构造入口/出口歧管来解决单罐温跃层储存系统中流量分布不均问题,通过数值模拟的方法比较非结构化歧管几何形状和具有优化挡板的歧管几何形状,发现提出的优化算法可以显著改善热性能,有效增加储热释热效率、容量比和总效率。
在创新罐体结构研究方面,Trevisan 等[41]构建了49.7 kWh 高温填充床储热器并在动态质量流量下进行实验研究,该高温填充床储热器通过内部管道实现了传热流体径向流动,如图5所示,结果表明,相对于静态条件,动态质量流速可导致热效率降低0.5%~5%。控制空气质量流速可以是一种有效策略,以在放热期间稳定热功率输出,同时使压降峰值最小化。Dong 等[42]提出了具有仿生静脉分级结构的填充床储热系统,在与传统均匀结构相同的孔隙率下,储热单元尺寸沿轴向和径向变化。数值结果表明,与传统的均匀结构相比,仿生静脉分级结构可以改善填充床的温度分布不均匀性,增加传热面积,改善热响应。Liu 等[45]提出了优化算法以形成基于静脉形成的流道,以提升相变材料吸热效率,从而最终提高太阳能甲烷重整过程中太阳能转换效率。
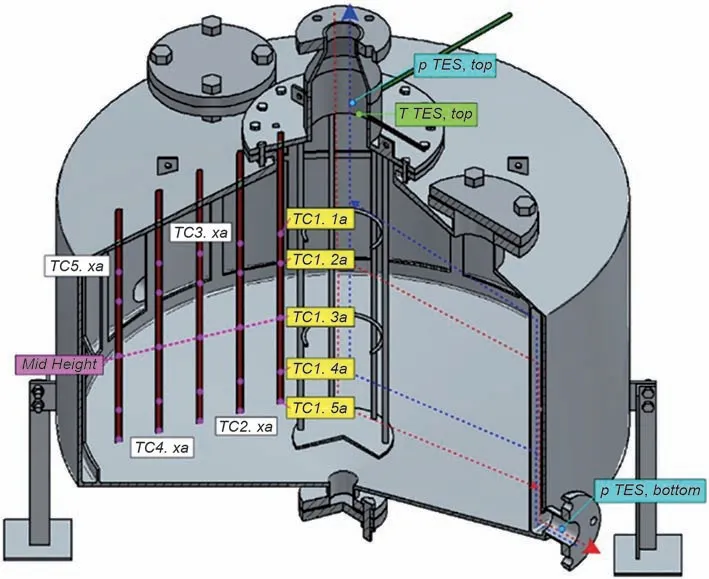
图5 高温填充床储热器外壳CAD设计,包括主要测量单元、内导管[41]Fig.5 CAD design of shell of high temperature packed bed heat accumulator,including main measuring unit, inner conduit[41]
填充床储罐设计是力学、流量分布、压降、热损失问题之间的权衡。一般来说,高径比大于1的圆柱形储罐通常是优选的,但每个系统的设计都应根据技术要求和成本进行综合考虑[16]。
3.2 传热流体
现有研究中,填充床储热系统多采用导热油或熔融硝酸盐液体传热流体,而气体传热流体多使用空气、高温烟气[16]。液体传热流体具有相对高的热容量和热导率,使得填充床储热系统能够在低循环速度下工作,因此适合应用于填充床储热系统。Bruch 等[46]采用最高运行温度为350 ℃导热油作为传热流体,对双介质填充床温跃层稳定性进行了实验研究,并建立一维两相数值模型而且通过双介质填充床储热和释热实验数据进行验证,如图6 所示,同时作者基于双介质填充床内部水力特性,开发了一种预测填充床压降的方法,该方法与实验测量数据具有非常好的一致性。同样以导热油作为传热流体,Mawire等[47]研究了不同入口质量流量的快速传热实验,从导热油平均温度、储热介质平均温度、平均储热功率和体积传热系数等方面分析了该装置的传热特性,发现入口平均质量流量增加会导致体积传热系数线性增加。同时作者总结了体积传热系数与表面质量流速和储热单元直径关系式:

图6 测量储热单元温度热电偶(左,红色),测量传热流体温度热电偶(左,蓝色),显示温度测量平面的储罐横截面(中间),未进行保温处理的储罐(右)[46]Fig.6 Implantation of the thermocouples in the gravel (left, red) and in the oil (left, blue).Cross-section of the storage tank illustrating the temperature measurement planes (middle).Each plane contains rock and oil TC following implantation presented on the left.Storage tank before insulation (right)[46]
其中hv是体积传热系数,d是储热单元直径,C1,C2为常数,G是表观质量流速,G定义为:
其中ρav为导热油平均密度,V̇ch为导热油平均体积流量,AT为装置横截面积。
Wu 等[48]通过数值模拟方法对在太阳能储热系统中应用的基于肉豆蔻酸球形胶囊填充床进行研究,分析了导热油入口温度、填充床初始温度和导热管质量流量对太阳能填料床储热系统放热过程中动态特性的影响。发现传热流体流速越快,储热放热速度越快。同时作者还发现传热流体温度和相变填充床热效率成正相关。
填充床储热系统也多采用空气作为传热流体。尽管空气的换热系数有限,但它确保了高安全性、低风险和低成本。Kuravi等[49]通过数值与实验研究手段,从流体分布和热分层方面证实了规整填充床的合理性,并且作者发现储热时间随着入口质量流量的增加而减少。Cascetta等[50]研究了填充床层的长径比、空气流量、温度水平和壁面惯性(以径向温度分布为重点)对储热性能的影响,发现通过降低传热流体质量流量,提高传热流体入口温度,增加填充床长径比,可以获得更好的储热效率。Singh 等[51]使用空气作为传热流体,在低空隙分数范围内对填充床进行了实验研究。Cascetta等[52]通过数值模拟方法,探讨了包括导热油、熔盐和空气三种不同传热流体下填充床储热装置的瞬态行为。发现经过几次储热释热循环后,导热油和熔盐依旧保持良好的性能,而空气的储热能力急剧下降。但空气也存在其优势,空气的使用温度范围广,不存在技术和环境问题。
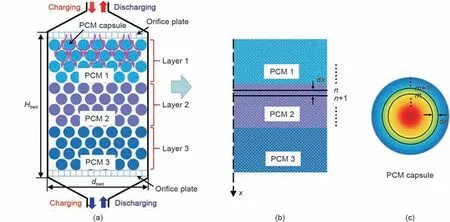
液态金属可在较宽温度范围内保持液态,并且具有高导热性,可实现高效传热,因此具有良好的应用前景。如图7 所示,Niedermeier 等[53]通过使用一维混合扩散模型,模拟分析了基于液态金属铅铋的相变填充床储热系统中填料参数对系统效率的影响。参数研究结果表明,对于液态金属双介质存储器中的有效放热过程,较小填料颗粒尺寸是有益的(d<10 mm),较大直径(10 mm 表2 不同文献中传热流体的选择Table 2 Selection of heat transfer fluids in different literatures 图7 双介质存储中的排放过程示意图,显示了储罐中轴向温度分布(x)和粒子内径向方向(y),红色:高温,蓝色:低温[53]Fig.7 Scheme of a discharge process in a dual-media storage showing the temperature distribution in axial direction in the tank (x) and intra-particle radial direction (y), red: high temperature, blue:low temperature[53] 相变填充床储热系统中储热单元的材料和尺寸由其使用用途、材料经济性等诸多因素确定[16]。相变材料一般需要封装成相变材料胶囊以避免相变材料熔化后泄漏[58]。大多数具有高能量密度的相变材料热导率较低[59],因此,人们提出了多种强化传热技术,包括提高导热系数、采用多种相变材料、增大传热面积等[60]。 封装相变材料储热单元常见几何形状包括长方体[37]、圆柱体[61]、球体[62]等,如图8所示。Wei等[63]通过数值模拟研究,将相变材料封装在四个不同的胶囊(球体,圆柱体,板状和管状)中,以研究不同相变材料封装结构的几何形状对储热系统的影响,发现球形胶囊显示出最好的放热性能。同时作者还发现对于球形和圆柱形胶囊,放热性能与空隙率几乎无关,对于板状和管状胶囊,孔隙率越大放热速度越快。Koide等[64]研究了含有Al-Si基微囊复合相变材料水平填充床在高温空气加热系统中的储热性能,随着气流速度增加,复合材料相变时间缩短,换热速度增加。Pakrouh 等[65]用数值模拟方法研究基于相变胶囊的相变储热系统在凝固过程中的性能,当相变胶囊直径从60 mm 减小到10 mm 时,直径减小导致相变胶囊表面体积比增加,提高了相变材料和传热流体之间的热传递速率,使得相变填充床热效率提高了11%。Tan[66]通过可视化实验研究了正十八烷相变材料在球体中的熔化过程,将熔化过程分为约束熔化和无约束熔化,并分别描述了其特点。发现在无约束熔化中,在开始时相变材料传热以导热为主。当相变材料熔化时,相变材料传热以自然对流为主。在约束熔化中,热传导只存在于熔化过程的开始。这种效应导致熔化的相变材料几乎同心向内熔化。Farid等[67]在一篇详细的综述中介绍了球形胶囊内相变材料的熔化和凝固。Sun等[33]通过数值模拟方法研究了棕榈酸/膨胀石墨/碳纤维复合相变材料中,球形胶囊直径、热导率和Stefan数对球形胶囊中相变材料熔化的影响。结果表明,球形胶囊直径减小可以提高熔化过程中的平均能量效率和㶲效率。 图8 不同几何形状的胶囊类型 (a) 长方体[37];(b) 球体[62];(c) 圆柱体[61]Fig.8 Different geometry type of capsules(a) cuboid[37]; (b) sphere[62]; (c) cylinder[61] 相变填充床储热系统强化传热技术还包括增大储热单元传热面积的方法。如图9所示,Tang等[58]提出一种具有中空通道的球形相变材料胶囊,并且分析了空心通道的角度和直径对热性能的影响,研究发现中空通道角度从30°减小到0°时,热性能下降了26.7%。Sun 等[68]提出一种带有环形翅片的双层球形相变材料胶囊结构并分析其热性能,结果表明,胶囊储热时间与翅片数量成反比,储热时间缩短14.4%,熵产随着翅片参数的增加而线性增加。Abdulateef 等[69]介绍了增强型储热系统翅片的几何参数和设计参数的研究。结果表明,纵向翅片结构由于易于设计和制造,得到最好的增强效果。Xu等[70]开发了椭球形宏观封装相变材料,通过实验研究了传热流体入口温度以及入口质量流量对相变填充床储热系统热性能的影响,研究发现与常规胶囊相比,椭球形宏观封装相变材料胶囊放热完成时间减少60%,但储热容量降低23%。Hu 等[71]发现外壳设计对金属和自然对流过程有显著影响,与矩形外壳储热单元相比,弯曲储热单元将储热时间减少30.6%。 图9 具有中空通道相变材料胶囊和普通相变材料胶囊 (a) 外观图;(b) 剖视图[58]Fig.9 Phase change material capsule with hollow channel and common phase change material capsule(a) Appearance view; (b) Sectional view[58] 仿生学借鉴自然界中生物的优异特性,可强化相变填充床中流动换热,提升相变填充床储热系统性能[72-74]。此外有研究学者将储热单元设计和仿生学联系在一起。Wang 等[74]提出一种仿生学肺泡结构储热单元,通过数值模拟和对其热性能进行分析,结果表明,与传统结构相比,仿生肺泡结构可以改善储热单元热响应,增加比表面积,并实现更快的填充床储热过程,双单元仿生肺泡结构和三单元仿生肺泡结构的储热效率分别提高6.4%和5.5%。如图10 所示,Dong 等[75]提出了仿生椭圆形结构储热单元,通过实验对其热性能进行了分析,结果表明,椭圆形胶囊的无约束熔化时间比球形胶囊短12%,椭圆胶囊平均努塞尔数比球形胶囊高20%。Cheng等[72]提出一种基于仿生学的红细胞形相变材料封装结构,通过数值模拟和实验对其热性能进行了分析,结果表明,与球形胶囊相比,其熔融时间明显缩短。Mohaghegh 等[76]提出了一种梨形相变材料胶囊,进行了实验和数值研究来分析其传热过程。结果表明,该结构增加了自然对流循环,使固液界面更加均匀,热性能更好。此外,增加翅片以扩大传热面积也是一种有效方法,尤其是在热阻较高的区域。虽然这些封装结构可以显著提高热能存储系统热性能,但由于其结构复杂在具体生产应用中具有挑战性。表3对部分储热单元几何形状的优化设计工作进行了总结,主要包括球体、圆柱体、板状、管状、不同仿生学结构等各种不同的封装结构。 表3 储热单元几何形状优化设计Table 3 Optimal design of geometric shape of heat storage unit 图10 胶囊从球形到椭圆形的演变[75]Fig.10 The evolution of capsule from sphere to oval[75] 根据以上不同学者对储热单元的研究可知,对相变材料进行封装可以减少相变填充床中的泄漏问题,延长相变填充床储热系统寿命,并解决了相变填充床储热系统在实际应用中的一部分问题。但是相变材料封装技术目前还存在重大技术挑战,例如封装外壳引起的高热阻问题。Ma等[79]基于焓-孔隙率模型和S2S辐射模型建立了相变填充床储热系统三维数值模型,由于相变材料是封装在储热单元中,因此研究了封装外壳对系统热性能的影响,发现封装外壳增加了传热流体和相变材料之间的热阻,降低了相变填充床储热系统的热效率,增加了储热时间。相变材料封装技术面临的挑战还包括封装外壳的形状稳定性、腐蚀问题,这些缺点极大限制了封装相变储热单元在工业上的大规模应用。为了应对相变材料封装技术存在的问题,近年来,人们将硅藻土、膨胀珍珠岩、膨胀蛭石或其他多孔陶瓷材料与各种盐类相结合制造出定型复合相变材料[80],定型复合相变材料的使用已被证明能够解决这些挑战。Ge 等[81]使用锂和碳酸钠的共晶盐作为相变材料,以氧化镁作为陶瓷骨架,以碳纳米管或石墨片薄片作为导热增强剂,制备出热导率超过4.3 W/(m·K),储能密度超过530 kJ/kg的定型复合相变材料。相比于相变材料封装储热单元,由于定型复合相变材料理想的热稳定性和出色的储热能力,定型复合相变材料更适用于相变填充床储热系统的实际应用。Li 等[61]以NaLiCO3作为相变材料、MyO 作为陶瓷骨架材料、石墨片作为导热增强材料,制备了定型复合相变材料,并建立基于该定型复合相变材料的填充床储热系统数值模型,研究了该定型复合相变材料的热性能,发现它具有较高热导率,并因此缩短了相变填充床储热系统储放热时间。作者还研究了定型复合相变材料在填充床内部的排列对储放热的影响,发现梯形排列布置的储放热时间最短,与平行和交错排列相比储放热时间分别缩短了55.6%和34.8%。Jiang 等[82]使用改性硅藻土、多孔陶瓷骨架和NaNO3盐制备出一种定型复合相变材料,研究发现这种定型复合相变材料在290~340 ℃温度范围内具有更高的储热密度,可用于填充床或平行通道中,并且作者还发现该定型复合相变材料易于集成到太阳能热能存储系统中。 目前我国余热资源利用比例低,大型钢铁企业余热利用率为30%~50%,其他行业则更低,余热利用提升潜力大[83],大量的工业热量被浪费到大气中,而这种有价值的能量可以通过相变填充床储热系统回收[14,50]。 在材料对基于相变填充床储热系统余热回收影响的研究中,Yagi等[84]开发一种利用相变材料回收500 K以上高温余热的储热工艺,并对单个封装相变材料和填充床进行了传热实验。从高能量密度储存、化学稳定性、无毒和性价比的角度测试了六种不同材料作为相变材料。从相变材料性能、流动方向和流速等方面对高温储热填充床进行了优化。结果表明,由于金属相变材料内部温度分布几乎均匀,因此金属相变材料比无机相变材料更适合相变填充床储热系统的应用。同时作者还发现将相变填充床储热和放热的传热流体入口设置成同一个入口有利于其储热释热。Luo 等[85]采用高热导率废塑料作为SiC 骨架吸附石蜡,制成绿色复合相变材料。作者采用数值模拟方法研究了基于开发的绿色复合相变材料填充床储热系统,对系统储热放热性能和流动特性进行数值模拟。结果显示,由于绿色复合相变材料的高热导率,系统储热和放热时间分别减少21%和41.1%。 在装置优化的研究中,Yu等[86]建立相变材料胶囊填充床储热过程的数学模型,研究了该装置热流体动力学特性。分析了传热流体入口速度、传热流体入口温度、相变储热单元初始温度和相变材料胶囊直径的影响。结果表明,传热流体入口速度增加导致填充床压降增加。当传热流体入口速度从0.01 m/s 增加到0.1 m/s 时,填充床泵功耗增加了24 倍以上。填充床中的规整填料结构导致了周期性流动特性,提高传热流体入口温度和传热流体入口速度加速了填充床的储热过程。填充床初始温度的升高并未影响储热时间,但总储热能力下降。当填充床初始储热温度增加10 K时,储热能力降低近165 J。梯级相变材料的填充床热能储存系统可用于低品位余热回收和利用,如图11所示,Guo等[28]设计了梯级相变材料填充床储热系统用于低品位废热回收利用,并对相变材料组成进行参数化研究,结果表明,当相变材料氢醌胶囊、己二酸胶囊和赤藓糖醇的容积比为3∶6∶1时,循环过程平均传热速率最高,约为0.559 kW,热效率最高值约76.1%。Liao等[87]建立修正瞬态一维混合扩散模型对岩石/相变材料胶囊组合填充床热性能进行数值模拟,结果表明,当具有截止温度的储热/放热循环达到可循环状态时,在储热过程中储存的热能几乎可以完全在放热过程中利用。储热/放热循环的截止温度对储热效率和容量比有很大的影响,当截至温度为209 ℃时,三次储热释热循环后储热效率稳定在96.1%,循环效率接近100%,容量比稳定在76.5%。柴油发动机废气作为余热气体排放到大气中,带走了大约30%的燃烧热量。通过提供适当的余热回收系统,可以节省大量热量。Prabu 等[88]将柴油发动机与相变储能系统结合起来,从废气中回收废热。储能系统由一个圆柱形不锈钢容器和40 个球形相变胶囊组成,该球形相变胶囊外壳由低密度聚乙烯制成,内部填充约100 g 石蜡。在这个系统中,水被用作传热流体。结果表明,4%~7%的总热量被该系统回收。 图11 (a) 填充床储热系统示意图;(b) 填充床储热系统计算域示意图;(c) 相变材料胶囊示意图[28]Fig.11 Schematic illustration of the PBTES system (a); the computational domains of the PBTES system (b);and the PCM capsule (c)[28] 在系统层面研究中,Manente等[89]提出了一种算法可实现储热材料选择与布局优化,用于提高钢铁行业中温下不连续波动烟气的热回收率,实现蒸汽或电力生产。所开发算法包括储热单元设计,以及对集成储热单元的系统进行性能评估。结果表明,通过与相变填充床储热系统的集成,双储罐布局优化产生的蒸汽量是完全混合储罐的两倍,与有机朗肯循环或卡利纳循环相结合发电量将会增加65%~70%,并且作者通过经济性分析发现,相变填充床储热系统由于硅油的高成本无法盈利。 4.2.1 太阳能集热器 太阳能是清洁无污染的可再生能源,并且在自然界中储量丰富,能够满足日益增长的能源需求,由于太阳能的间歇性和不稳定性[90],太阳能供应和能源需求之间存在着不匹配。相变填充床储热系统通过在非高峰时段期间从太阳能场收集能量,然后在需求的高峰时段期间释放能量[91],从而减少太阳能供应和能源需求之间的不匹配问题。 前期在相变填充床与太阳能集热器的研究中发现,太阳辐射强度的实时变化会导致太阳能集热器出口温度不稳定,对相变填充床储热系统的热性能产生重要影响。如图12所示,Wang等[31]研究了与太阳能抛物面槽集热器集成的相变填充床储热系统动态热性能,包括不同质量流量对系统总储热容量、总㶲输入和总㶲效率的影响。结果表明,稳态和不稳定入口边界条件的热性能存在显著差异。在不稳定边界条件下,质量流量越大,温差越小。在稳态入口温度条件下,随着质量流量的增加,㶲效率逐渐降低。不同气象条件的变化会导致相变填充床入口温度产生波动,Elfeky 等[92]研究了入口温度波动对不同储存配置储罐热性能的影响,提出并验证了一种两相混合扩散模型来分析系统的周期热特性。结果表明,混合显热相变储存在入口温度变化时具有最高的容量比、利用率、回收能量和总效率,此外,研究结果证明,在低温下使用显热相变配置的总效率提高了19.2%,而在更高的温度下提高了34.4%。如图13所示,Bouadila等[93]进行了一项实验研究,评估一种新的太阳能空气加热器热性能,该加热器使用了相变填充床储热系统,储热单元是相变球形胶囊,结果表明,每日能效在32%~45%之间变化,而日㶲效率在13%~25%之间变化。Arfaoui等[94]为了提高太阳能空气集热器效率,从运行时间、出口空气温度和启动运行时间等方面提高其热效率,如图14所示,研究了一种基于相变储能的紧凑型太阳能空气集热器性能。以CaCl2·6H2O作为相变材料并封装在球形胶囊中,实验结果表明,在储热过程中,储存的热量随着吸收太阳辐射的增加而增加,每日能效在47%左右。在太阳能干燥机中,干燥过程很大程度上取决于当地不同的天气条件,导致干燥产品的质量较差。为了消除热空气温度的波动,Esakkimuthu 等[95]将太阳能集热器与相变填充床储热系统相结合,以存储更多的太阳能,并在恶劣天气期间可用能量不足时释放太阳能。结果表明,在高质量流速下,收集器效率更高,这是由于除了在更高质量流速下传热系数值增加之外,与太阳能集热器平均温度降低导致相关的热损失也减少。Nallusamy 等[96]通过实验研究显热和相变组合式热能存储单元的填充床热行为,并且将填充床与太阳能集热器集成在一起,以石蜡作为相变材料并填充在球形胶囊中,结果表明,在填充床与太阳能集热器集成的情况下,质量流量对太阳能集热器的热提取率有显著影响,并且会反过来影响填充床储热率。Saitoh等[97]提出将具有盐水合物的填充床储热系统与传统太阳能收集器集成,用于建筑供暖和热泵系统。 图12 不稳定状态入口温度条件下不同质量流速下450 min的温度分布和液相率分布[31]Fig.12 Temperature distribution and liquid fraction distribution at 450 min at different mass flow rates under unstable-state inlet temperature conditions[31] 图13 实验级太阳能集热器照片[93]Fig.13 The photograph of experimental the solar air heater with latent storage collector[93] 图14 双床相变储能太阳能空气加热器实验设置[94]Fig.14 Experimental set-up of the solar air heater with latent storage energy on two beds[94] 4.2.2 聚光太阳能发电 相变填充床储热系统在聚光太阳能发电中的应用具有悠久历史。高温储能系统对于提高聚光型太阳能电站的效率具有重要作用。相变储能因其储热密度大且相变过程中温度近似恒定而成为最具竞争力的热能存储方法之一。Ma 等[79]在研究中,建立了一个三维填充床模型来研究使用AI-25%Si 合金作为相变材料的高温相变储能系统热性能。由于金属合金相变材料的高热导率,使用相变材料系统的平均功率高于使用岩石系统的平均功率。 在对相变储热材料的特征优化工作中,Gautam等[90]分析了球形表面上的孔隙对填充床储热系统性能的影响,并试图优化储热元件参数。探讨了孔深度与孔径比、穿孔指数和孔球径比等设计参数,温升参数和雷诺数等操作参数对填充床储热系统性能的影响,并从热工水力效率的角度提出了全局优化策略。发现当雷诺数从200到550过程中,热工效率随之增加,雷诺数从550到800过程中,热工效率随之下降。并且作者还发现在平均日照为1000 W/m2,孔径与小球直径比等于0.2,孔深度与小球直径比等于0.0066,穿孔指数等于0.18 的条件下,具有最大热工效率89.87%。Nithyanandam 等[98]分析具有封装相变材料的填充床储热系统的动态热行为,该系统经受部分储热和放热循环,以及在聚光太阳能发电工厂运行中遇到的储热和放热温度的限制。结果表明,半径较小胶囊产生较高总利用率和潜在利用率。较大传热流体的雷诺数带来较高的质量流量,但由于热交换区的膨胀,导致系统利用率的降低。Yue 等[99]开发了基于相变填充床储热系统、二氧化碳布雷顿循环、有机朗肯循环的聚光太阳能发电系统,研究了相变材料胶囊储热罐排放过程中太阳能发电厂的动态热性能,结果表明,热能储存罐中传热流体速度可用于控制太阳能热力系统的瞬态功率输出。使用小型储热胶囊是提高聚光太阳能联合循环系统热性能的有效方法。热能存储系统受到出口阈值温度的约束,因此优化不同熔化温度相变材料的温度分布是提高相变热能储存系统性能的有效途径。Li等[100]建立了带有相变材料胶囊的填充床储热系统数学模型,并且相变热能储存系统在储热放热过程中受到出口阈值温度的约束。基于该模型,研究了熔化温度对非梯级、双层和三层相变热能储存系统性能的影响。结果表明,对于非梯级相变热能储存系统,相变材料的有效利用率在很大程度上受到熔化温度的影响,最大利用率只有40%左右。对于双层或三层梯级的相变热能储存系统,通过选择合理的熔化温度,可以大大提高相变材料有效利用率。 储热系统是太阳能热电站提高可靠性的关键系统。温跃层稳定性对于阐明和提高相变填充床的性能具有更重要意义。Reddy 等[101]采用非热平衡模型,研究了热能容量为150 kWh/m3填充床储罐在高流量条件下的温跃层稳定性、绝热壁面和非绝热壁面条件下的排放效率,发现当雷诺数等于1 时,填充床储罐具有5.84 h的优异释热效率,同时发现当雷诺数从1增加到3000时,释热效率持续下降。Flueckiger 等[102]建立一种新型有限体积计算模型,用于模拟装有封装相变材料的填充床内的质量和能量传输,将该热能储存模型集成到100 MW CSP工厂的系统级模型中,将该相变填充床和传统石英岩填充床进行一对一比较,发现相变填充床比传统石英岩填充床输出功率增加了9.7%。 本文综述了相变填充床储热系统的性能研究及其优化设计和应用。首先介绍了相变填充床储热系统的数值研究,包括舒曼模型、单相模型、连续固相模型、混合扩散模型。然后,讨论了相变填充床储热系统基于能量和㶲效率的性能分析。此外,还总结了该系统的各种优化设计,如储罐结构设计、传热流体的选择、球形胶囊的形状、结构以及封装方法。最后,详细介绍了相变填充床储热系统在工业余热回收和太阳能回收装置余热回收的相关应用。主要结论如下。 (1)基于多孔介质的两相模型已被广泛用于相变填充床储热系统的充放热过程。舒曼模型既不考虑流体中的传导,也不考虑固相中的传导,大大简化了求解的复杂性,因此舒曼模型的计算量较小,但其反映流体温度分布和填充床温度分布的准确性较低;连续固相模型考虑了轴向和径向热传导,连续固相模型可以分析储放热过程中径向热梯度的影响,这对于研究热损失大或入口流量分布不均匀的相变填充床储热系统具有重要意义;混合扩散模型考虑了相变材料胶囊内部的热梯度,与舒曼模型、连续固相模型相比,混合扩散模型可更准确地反映出填充床储热的瞬态热行为,计算量更大。 (2)填充床储罐的设计是力学、流量分布、压降、热损失问题之间的权衡。能量效率与㶲效率是评判相变填充床储热系统的重要指标,包括调节填料粒径、控制传热流体入口温度、设计梯级填充层等手段,都可以提升填充床效率。在储罐设计中,高径比大于1的圆柱形储罐通常是优选的,同时每个系统都应从技术要求和成本考量开展定制优化;导热油、熔融盐、空气、高温烟气等介质多被用作传热流体,液态介质具有更好的传热能力,而空气介质具有高安全性、低成本的特点;储热单元的优化设计方法的选择对提升填充床性能至关重要,包括采用金属球形外壳、仿生学结构等方法,可以有效提升储热单元热响应,强化热效率。然而,目前的封装方法具有生产成本高、难度大的缺点,在具体生产应用中具有挑战性。 (3)相变储热填充床的应用主要体现在工业余热回收和太阳能收集装置余热回收等领域,目前在余热回收领域主要针对发动机废气、钢铁生产过程烟气等行业,目的为回收利用废热以提升工业过程能效。在太阳能热能收集中,家用太阳能集热器及工业聚光太阳能发电中均可提升能量效率。相变储热填充床的应用可有效平衡工业余热和太阳能的产量波动、温度不稳定性和空间分布不均匀性等问题,实现能源的高效回收和利用。 本文工作重点是评估相变填充床储热系统优化设计对热性能的影响。目的是总结每种技术的思想、差异和局限性,并进一步分析可能的新优化方向。对于填充床储热系统储罐设计、储热单元设计、传热流体选择,在未来工作中应进一步研究填充床热棘轮(例如相变体积变化导致的构件形变)、储热单元的定型性能(例如利用多孔骨架吸附)以及传热流体和相变储热单元长期相容性等问题。对于相变填充床储热系统数值模型,在未来工作中,应考虑高温环境的热辐射问题,这对相变填充床储热系统的数值模拟是一个巨大挑战。对于储热单元的优化设计,基于仿生学原理的储热单元设计是一种新兴优化设计方法,但许多研究不符合仿生学原理,因此在这方面的未来工作中,应进一步研究在相变填充床储热系统中符合仿生原理意义的储热单元设计。相变填充床储热系统的运行策略影响着填充床内部的储热释热过程,如何在不稳定和不连续的外部环境中实现系统的实时调节,保证相变填充床储热系统高效稳定的能量输出,是其面临的关键问题,目前相关研究较少,建议在未来工作中加深其相关工作内容。相变填充床储热系统广泛应用于工业余热回收和太阳能热能收集等领域,但是大部分研究局限于实验室中,应进一步研究在不同应用领域系统设备的集成以及相变填充床储热系统的成本效益。推进上述问题的研究对于推进相变填充床储热系统在更高温、更大规模尺度上的应用具有重要意义。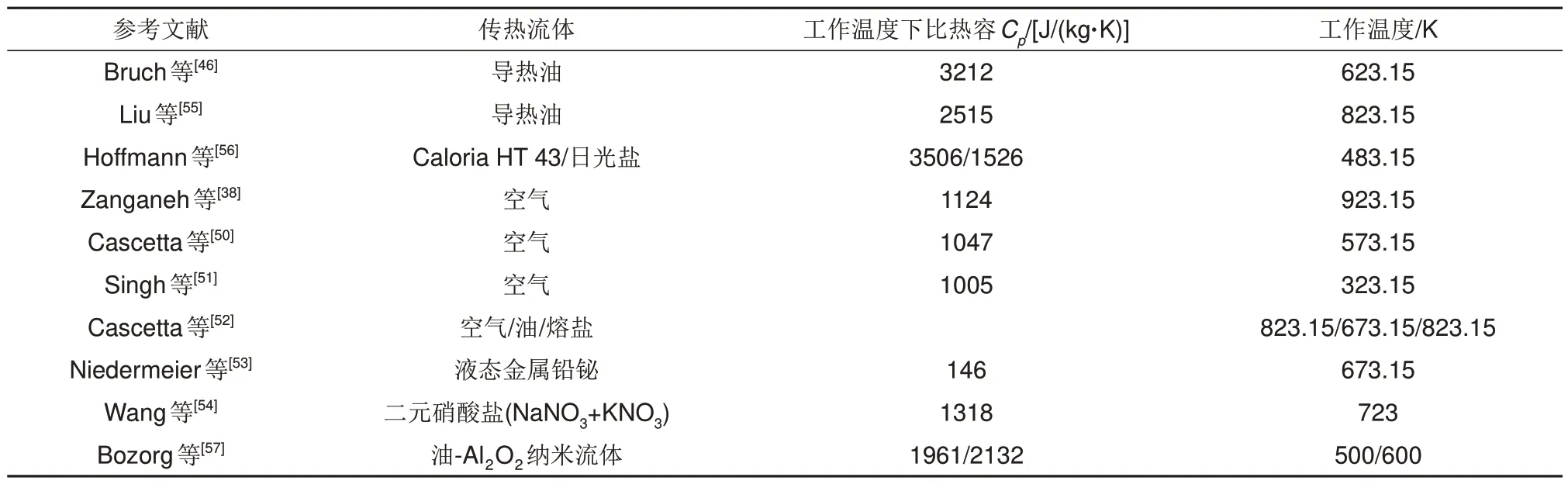

3.3 储热单元




4 应 用
4.1 工业余热回收
4.2 太阳能热能收集



5 结 论
—— 储罐

