基于复合标定和极限学习机的关节臂式坐标测量机残差建模及补偿

高贯斌， 谢 佩， 刘 飞， 那 靖

（昆明理工大学 机电工程学院，云南 昆明 650500）

1 引 言

关节臂式坐标测量机（Articulated Arm Coordinate Measuring Machines,AACMM）是一种采用旋转角度为测量基准的便携式三坐标测量设备，与测量软件结合可以进行长度、角度、平面度、同轴度、圆度等几何特征的测量［1］。关节臂式坐标测量机具有通用性强、测量范围大以及方便现场测量等优点，在汽车制造、模具设计、零件检测、设备维护等领域得到应用［2］。与传统三坐标测量机相比，关节臂式坐标测量机的精度较低，限制了其在高精度领域的应用。因此，如何进一步提高关节臂式坐标测量机的测量精度一直是本领域的研究热点。

引起关节臂式坐标测量机误差的因素可分为静态因素和动态因素。静态因素主要是由运动学参数误差引起的，可采用运动学标定的方法解决［3-5］。因为工业机器人与关节臂式坐标测量机结构类似，所以二者的运动学标定方法相似且主要集中于建模、测量、参数辨识和误差补偿方面。

运动学参数辨识的研究主要集中于引入智能搜索算法、构建适当的辨识策略以快速准确地求解运动学误差方程。Cholmin 等［6］提出了一种小生境混沌优化算法（Niche Chaotic Optimization Algorithm）并运用到关节臂式坐标测量机的运动学标定中，有效地降低了均方根偏差。Chen等［7］将改进甲虫算法应用到KR500L340-2 型工业机器人进行运动学参数辨识中，在完成参数误差补偿后KR500L340-2 的位置误差平均值从2.95 mm 减小到0.20 mm。另外，内点法［8］、L-M算法［9］和改进教学-模拟退火算法［10］等也被应用于关节式机器人的参数辨识之中。然而，关节臂式坐标测量机的运动学参数数量多，构成的参数辨识矩阵维度高，使得智能优化算法的求解效率低且易陷入局部最优［11］。

运动学建模方面主要致力于使得关节臂式坐标测量机的运动学模型变得完整、非冗余且连续。Benciolini 等［12］提出了基于四元数的关节臂坐标测量机运动学新模型用以避免D-H 模型平行关节不连续的问题。冯旭刚等［13］将广义几何误差模型运用到关节臂式坐标测量机运动学建模当中，克服了D-H 模型不连续和无法包含静态柔性误差的问题，有效地提升了关节臂式坐标测量机的测量精度。此外，MCPC 模型［14］、POE 模型［15］和多传感器坐标测量机参数模型［16］等也被应用于关节式机器人的运动学建模之中。其中POE 只需要两个参考坐标系（工具坐标系和基础坐标系）就可表达出机械臂末端执行器工具坐标系相对于其基础坐标系的位姿，但是，POE 仍然无法摆脱参数冗余和计算量大的问题［17］。

为了求解关节臂式坐标测量机或机器人的运动学参数误差方程，通常需要准确测量末端位姿信息或进行有效物理约束。可用于关节臂式坐标测量机末端位置测量的仪器主要有激光跟踪仪、光学动捕系统、相机［18］等。但是，激光跟踪仪价格高昂且需要特定的夹持装置对关节臂式坐标测量机进行固定，在实际应用中不现实且操作繁琐，动捕系统布置周期长且所需空间大，相机的测量精度通常是达不到0.1 mm 从而无法满足测量精度要求。目前，工业现场主要采用锥孔约束测头进行关节臂式坐标测量机自标定的方法，无需外部测量仪器，便于在现场应用。但是传统自标定采用的是单点重复标定方法，单点重复标定只能将角度参数准确辨识出来，长度参数存在等比例缩放的问题，需要借助精密测量设备对部分长度参数进行测量并在辨识中进行固定。为此提出一种基于单点和空间距离的复合自标定方法完成运动学标定，用以弥补传统自标定方法的不足。

关节臂式坐标测量机受重力、轴系晃动、关节回转不均匀等动态因素影响而产生的误差称为残余误差，残余误差无法通过运动学标定消除。目前，关节臂式坐标测量机残差补偿方法可分为两大类，第一类是研究残差特性，建立残差与测量构型等变量的关联模型，进行残差预测和补偿；第二类不寻求建立模型，而是基于神经网络，根据测头位置或关节转角进行残差预测和补偿。

Hamana 等［19］分析了局部关节挠度带来的误差，基于测量姿态进行了残差补偿建模补偿。许铀等［20］分析了多关节测量系统关节角度与末端执行器残差之间的关系，并建立了残差数据库以修正系统误差。高群等［21］提出一种基于多项式模型的单点测量残差校正方法，研究了圆柱坐标系中关节旋转角度与残差之间的关系，建立的多项式误差补偿模型，并补偿了关节臂式坐标测量机的残差。

Zhao 等［22］提出了一种使用LM 算法进行运动学误差标定，然后使用由思维进化算法优化的反向传播神经网络进行非运动学误差补偿的方法。类似地，工业机器人的残差补偿方法对关节臂式坐标测量机也存在借鉴意义。Zhao 等［23］使用激光跟踪仪大规模测量不同构型下末端位姿信息，以关节转角为输入、实际位姿误差为输出，建立了一种基于深度神经网络残差补偿模型，以KUKA 工业机器人为实验对象完成了残余误差补偿实验，使得机器人的最大误差由1.96 mm 减小到0.22 mm。Nguyen 等［24］在运动学标定的基础上设计了一个三层的人工神经网络用于拟合1到3 关节与机器人残余误差之间的非线性关系，完成PUMA560 型工业机器人非几何误差补偿模型的建立，补偿后机器人的误差从4.065 4 mm下降到0.336 8 mm。

综上所述，残差建模的方法为了构建补偿模型方便，通常在第5 关节坐标系中建立残差补偿模型，需通过变换才能得到基坐标系下的残差补偿值，在转换的过程中难免会引入转换误差，从而影响补偿效果。基于神经网络的“黑箱”式残差补偿方法，需要工作空间采集大量数据用于训练网络，才能保证残差补偿泛化性，但是，关节臂式坐标测量机通常具有6 个或者7 个关节，这么高的维度下需要的数据是海量的，而且测头的三维空间位置坐标的准确值测量也非常困难。

针对上述问题，本文通过构建测量构型与残差的关系，提出一种在测头坐标系的基于复合标定和极限学习机的关节臂式坐标测量机残差补偿方法，其数据量需求少、效率和精度高，本文的主要贡献和创新点总结如下：

（1）针对关节臂式坐标测量机标定中长度参数具有等比例缩放现象，辨识出来的长度参数不准确的问题，提出一种依次进行角度参数辨识、长度参数辨识和长度参数等比例缩放的复合辨识方法，完成了七自由度关节臂式坐标测量机的运动学标定。

（2）通过对标定后关节臂式坐标测量机残余误差分布图谱分析，发现残余误差与测量构型参数之间存在密切关系，通过基坐标系原点、第四关节坐标系原点和第六关节坐标系原点构建了以测量摆角、仰角、距离和转角为变量的测量构型，由于测量构型与残余误差存在高阶非线性关系，本文采用极限学习机（Extreme Learning Machine， ELM）建立残余误差补偿模型，对残余误差进行补偿。

（3）利用本文提出的复合参数辨识和残余误差补偿方法对关节臂式坐标测量机进行了标定和补偿实验，结果证明了本文所提模型及方法可有效提高关节臂式坐标测量机的精度。

2 运动学建模及标定

2.1 运动学正解及运动学误差建模

本文以某通用型7 自由度关节臂式坐标测量机作为测试对象，如图1 所示，其由基座、2 个连杆、7 个旋转关节和测头组成。

图1 某通用型7 自由度关节臂式坐标测量机Fig.1 7-DoF articulated arm coordinate measuring machine

2.1.1 运动学正解

本文采用D-H 方法对关节臂式坐标测量机进行运动学建模，D-H 法中定义了四个参数，分别是关节长度、杆件长度，杆件扭转角和关节转角。其中四个参数的定义如下［25］：

关节长度ai-1：沿xi轴上zi-1与zi之间的距离；

杆件长度di：沿zi-1轴上xi-1与xi之间的距离；

杆件扭转角αi-1：从zi-1到zi绕xi轴旋转的旋转角度，绕xi逆时针转向为正；

关节转角θi：从xi-1到xi绕zi-1轴旋转的旋转角度，绕zi-1逆时针转向为正。

根据D-H 法建立得到关节臂式坐标测量机的坐标系统，如图2 所示。

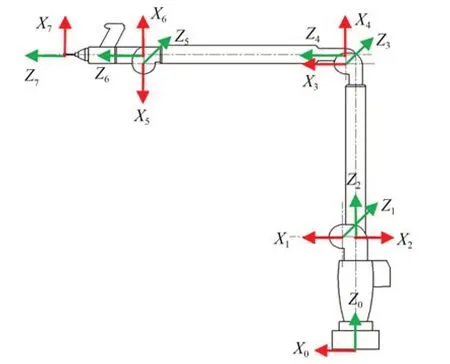
图2 关节臂式坐标测量机坐标系统Fig.2 Coordinate systems of the AACMM

每个关节坐标系有4 个运动学参数，测头有3个参数，则七自由度关节臂式坐标测量机共有31个运动学参数。对关节臂式坐标测量机的结构进行初始测量可得这些参数的初始值，如表1所示。

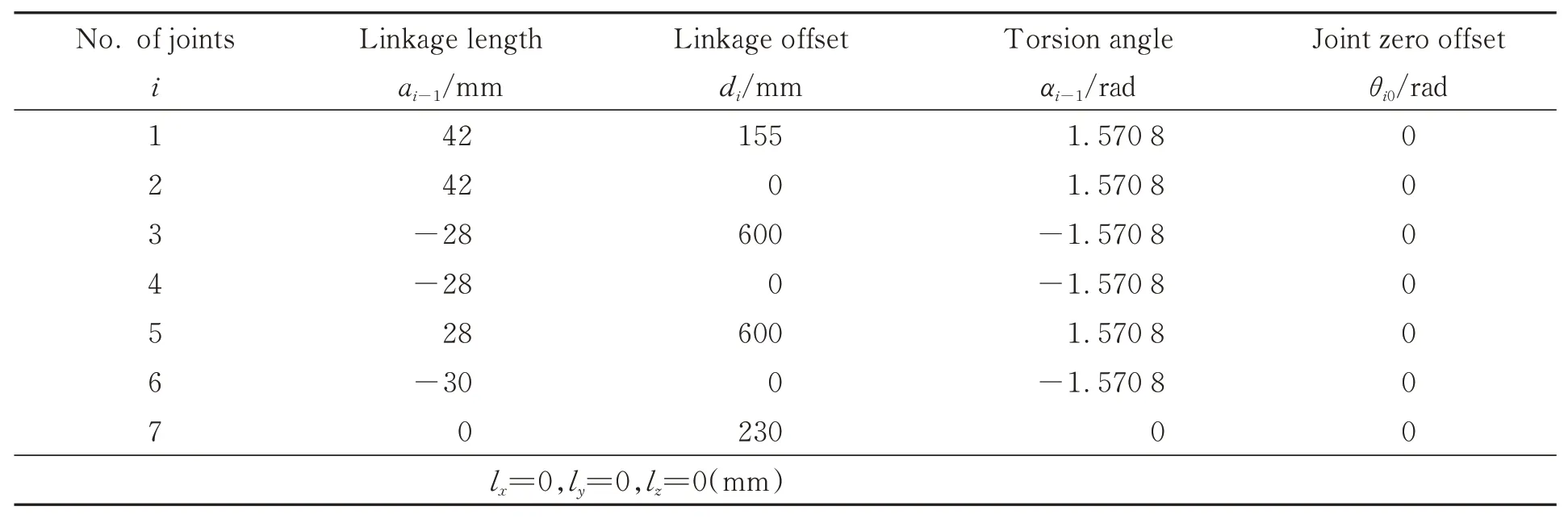
表1 运动学参数初始测量值Tab.1 Nominal value of kinematic parameter

完成关节臂式坐标测量机的运动学建模后，通过平移和旋转可以得到坐标系｛xi-1，yi-1，zi-1｝到｛xi，yi，zi｝的齐次变换矩阵Ti-1，i：

通过依次右乘相邻关节坐标系变换矩阵，可得到第7 关节坐标系在基坐标系下的位姿矩阵：

将T0，7右乘齐次化测头偏置向量（lx，ly，lz，1）T，可得到测头在基座坐标系下的齐次坐标（x，y，z，1）：

2.1.2 运动学误差建模

通常可以将关节臂式坐标测量机的测头固定于一锥孔中，以保持测头球心位置不变，通过改变各关节转角，获得一系列的关节转角数据，利用这些数据通过式（3）计算出的测头坐标值理论上应该是相同的［26］，但由于运动学参数存在误差的原因，实际上计算得到的测头坐标值并不相同，测头坐标的重复性误差反映了运动学参数的误差。因此，可以将测头在某一锥孔点的重复误差作为目标函数，通过最优化方法对运动学参数进行辨识。

测头的单点重复误差ΔP主要由运动学参数误差（Δdi，Δαi-1，Δai-1，Δθi0，Δlx，Δly，Δlz）所决定，其中Δdi为杆件长度误差、Δai-1为关节长度误差、Δαi-1为杆件扭转角误差、Δθi0为关节转角零位误差、（Δlx，Δly，Δlz）为测头偏置误差。这些偏差通常足够小，因此可以用微分运动原理建立运动学误差模型，即：

进一步写成矩阵形式：

其中，PN表示测头的名义坐标值，Δk是参数误差矢量，，i=1，2，3，…，7，表示单点测量时测头的平均坐标值，即：

Jk是雅克比矩阵：

2.2 运动学参数辨识

基于刚体微分法建立的误差模型是一个线性方程组，若有N组末端测头坐标值和关节转角数据，则由式（5）可得：

为求得运动学参数误差向量Δk，可将式（8）转化为最小二乘问题，即：

由于采用单点标定的方法缺少距离信息，仅能够辨识出运动学参数中的角度参数（Δαi-1，Δθi0），而长度参数（Δdi，Δai-1，Δlx，Δly，Δlz）难以被准确辨识出来。针对上述问题，Cheng 等［27］提出了一种对长度参数进行等比例放缩的方法对长度参数进行标定。此方法对长度参数进行等比例放缩，只会影响长度测量结果，并不会影响关节臂式坐标测量机的单点精度。如果利用两个锥孔距离提供的长度信息，则可以辨识长度参数。若只考虑长度参数误差，根据式（5）可知位置1 处和位置2 处的误差分别为：

两个位置的距离误差为：

令JL=Jk1-Jk2，则有：

为求得长度参数误差向量ΔkL，将式（12）转化为最小二乘问题，即：

上述方法能够对运动学参数中的长度参数进行辨识。完成长度参数辨识、提升单点测量精度后，再采用等比例放缩法可以进一步提升长度测量精度。因此，本文采用角度参数辨识、长度参数辨识和长度参数放缩三种方法分步进行的策略对运动学参数进行辨识，流程如图3 所示。

图3 复合标定法流程Fig.3 Flow chart of compound calibration method

3 残余误差补偿建模

运动学标定能消除静态因素引起的误差，然而想要进一步提高关节臂式坐标测量机的测量精度及稳定性则需要进行非运动学标定，消除动态因素引起的残差。影响关节臂式坐标测量机测量精度的动态因素主要集中在第2 关节到第6关节之间［28］，因此，本文着重分析了2 到6 关节之间的动态因素对测量精度的影响。

关节臂式坐标测量机的连杆和关节部分的质量并不是均匀分布，且测量构型的变动会导致关节臂式坐标测量机的重心发生变化，所以无法对重心位置进行准确地数学建模。同样地，也没有确定的数学模型能对回转不均匀和轴系晃动误差等动态因素进行严格描述。但与这些动态因素密切相关的关节臂式坐标测量机的测量构型却是可以用数学建模的方法得到。因此，关节臂式坐标测量机受动态因素的影响的问题可以转化为残差与其测量构型之间的关系问题。

3.1 测量构型与残差的关系建模

在使用关节臂式坐标测量机进行测量时，一旦第1 关节、第2 关节和6 关节的转角确定，则第4 关节在空间的位置也就确定了下来，即测量构型确定了。反之，每次测量，只要基坐标系原点和测头位置确定，最后只需要确定第4 关节的位置就能使得关节臂式坐标测量机的测量构型确定。因此，关节臂式坐标测量机的测量构型可以由基坐标原点位置、第4 关节坐标系原点位置和测头位置决定。

对于任意测量任务来说，只要基坐标系和第六关节坐标系位置固定，进行摆臂测量时第4 关节在测量空间中构成近似于圆形的轨迹（如图4），本文将其称之为构型圆。

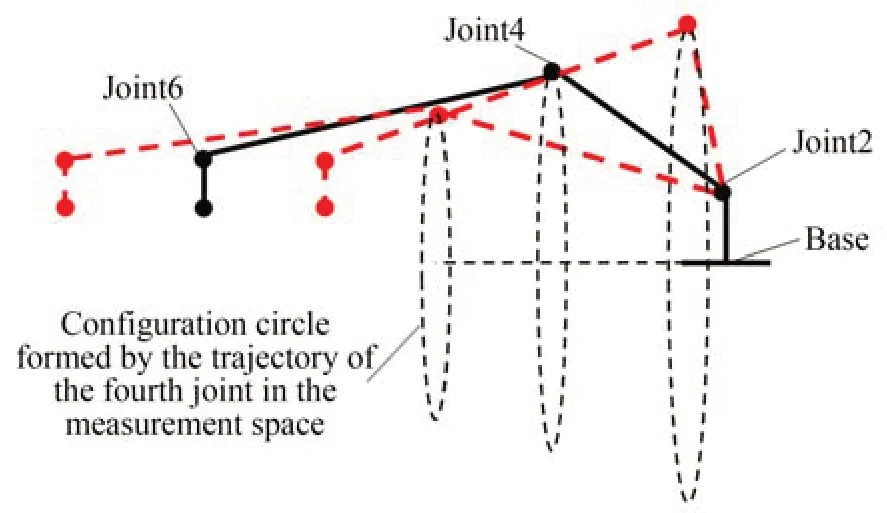
图4 第4 关节在空间中的轨迹Fig.4 Track of the 4th joint in the measurement space

图4 表明，无论采用哪种测量构型进行测量，第4 关节一定落在对应的构型圆上，只是在构型圆上的位置和构型圆的半径有所不同。因此，关节臂式坐标测量机的测量构型可由第4 关节所在的构型圆及其在构型圆上的位置决定。

首先分析第4 关节在任意构型圆上位置有相关联的因素。定义基坐标系原点、第4 关节坐标系原点和第6 关节坐标系原点组成的平面为D1，令基平面为D0，则如图5 所示，第4 关节在构型圆上的位置与D1和D0的夹角ω有关。

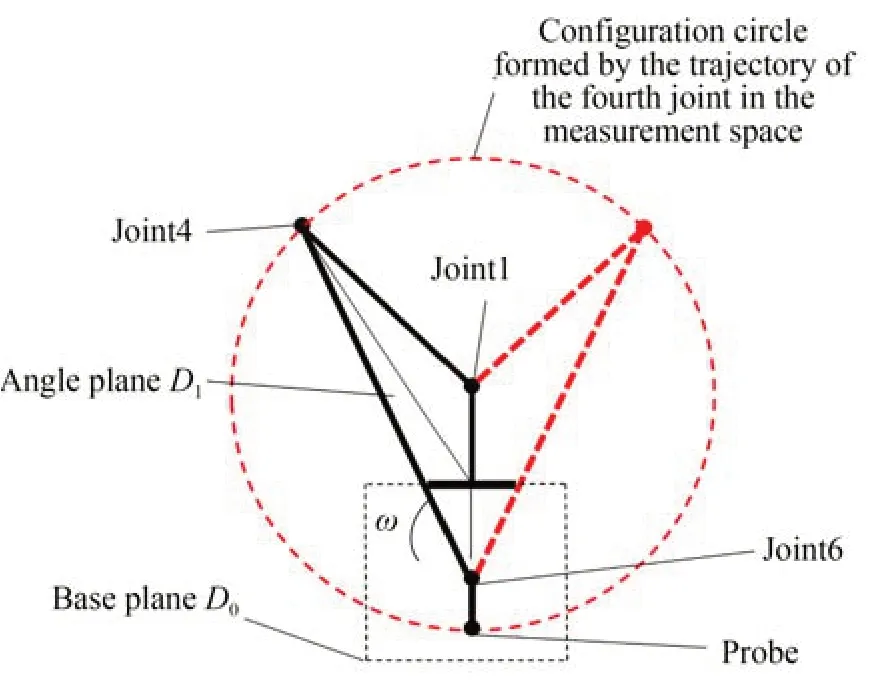
图5 测量摆角ω 示意图Fig.5 Diagram of measuring swing angle ω

摆角ω可以由D1与D0对应的法向量之间的夹角表示。D0的法向量V0可表示为V0=［0，0，z］。其中z表示测头在Z轴方向的坐标值。D1的法向量V1可以表示为：

其中：P4i表示第4 关节在基坐标系下的坐标值，是齐次变换矩阵T0，4的第4 列的1～3 行；P6i表示第6 关节在基坐标系下的坐标值，是齐次变换矩阵T0，6的第4 列的1～3 行：

完成法向量V0和V1的求取后即可根据空间向量夹角公式求得摆角ω：

上述摆角ω表示了第4 关节在任意构型圆上的位置，接下来需要进一步分析第4 关节具体位于哪一构型圆上。第4 关节具体在哪一构型圆上的问题实际就是分析构型圆的半径和哪些因素有关。如图6 所示，基坐标系到第6 关节的连线与基平面之间的夹角和第6 关节坐标原点与基坐标原点之间的连线长度决定了第4 关节到基座的距离。第4 关节到基座的距离一旦固定，那么构型圆的半径也就随之确定。令第6 关节坐标原点到基坐标原点的连线与基平面之间的夹角为仰角vmc，定义第6 关节坐标原点与基坐标原点之间的连线长度为长度Lmc，而构型半径的大小可由仰角vmc和长度Lmc所决定。

图6 构型圆位置和半径示意图Fig.6 Diagram of the position and radius of the configuration circle

vmc实际是P6i与基平面法向量V0之间的夹角，同样根据空间向量夹角公式，得到仰角vmc的表达式：

Lmc实际就是第6 关节坐标原点到基坐标系原点的欧氏距离：

虽然测头部分（第6 关节到测头）和第1 关节的动态因素可以忽略，但是它们转动会对残差值造成一定的影响。为了得到较为精确的残差补偿模型，下面依次分析第1 关节和测头部分对残余误差值的影响。如图7 所示，当测量构型固定时，将测头与基坐标系原点的连线投影到XY平面中，连线会随着第1 关节的转动与X轴成不同大小的夹角θr（本文称之为转角）。转角θr的改变则会使得同一测量构型下X和Y方向的残差值发生改变，但本质上是构型圆在空间中的位置发生了变化，从而使得第4 关节的位置发生改变。因此，在构建测量构型参数时应当将θr考虑进去，θr可以用以下公式求得：

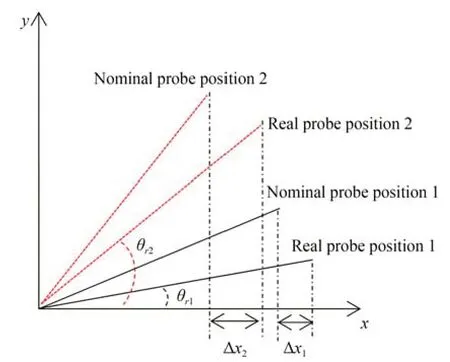
图7 第一关节对残差的影响Fig.7 Effect of first joint on residual value

下面分析测头部分旋转会对残差值的影响，如图8 所示，当关节臂式测量机的测量构型确定后，测头部分可以绕第6 关节进行旋转形成圆形轨迹，本文称之为测头圆。由于测头部分的动态因素忽略不计，所以真实的测头圆和名义上的测头圆半径相同，且测头在测头圆上的位置相同。

图8 测头部分在空间中形成的轨迹Fig.8 Circular track formed by probe in moving space

为了分析测头部分旋转会对残差值的影响，下面将测头圆投影到XZ平面进行分析。如图9所示当测头部分绕6 轴旋转时，测头圆的圆心与测头的连线与X轴形成夹角θp。θp的大小不同可能会对残差值产生影响，故需要分析θp与残差值之间的数学关系。为了便于分析，令Lp为测头圆的半径、Lrz为两个测头圆之间Z方向的圆心距、Lrx为两个测头圆之间X方向的圆心距。根据几何关系可以求得X，Z方向上残差值的表达式为：

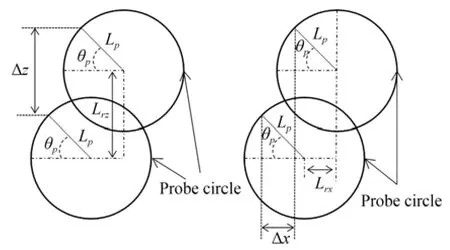
图9 测头圆对残差值的影响Fig.9 Impacts of probe circle on residual value

从式（20）可知，Z和X方向上的残差值实际上只与两测头圆之间的圆心距有关（Y方向同理）、与θp无关，而圆心距只与测量构型有关。因此可知测头部分绕第6 关节的旋转不会对残差值产生影响。

基于上述分析，本文最终以ω，vmc，Lmc和θr四个参数来描述关节臂式坐标测量机的测量构型。测量构型参数（ω，vmc，Lmc，θr）与关节臂式坐标测量机残余误差之间的关系如图10 所示。

图10 测量构型参数与残差Fig.10 Relationship between configuration parameters and residuals

下面通过残差分布图谱来分析测量构型参数与残差之间的关系。利用锥孔采集多摆角单点数据，可以计算得到相应的测量构型参数和残差，绘制残差分布图谱如图11～图13 所示。可以看出2 个测量构型参数和残差之间存在明显的规律，其形成了一个二维曲面，但其与现有的可用函数描述的曲面均不相同，因此，很难通过数学建模的方法对其进行描述，需要找到一种合适的方式将测量构型参数和残差的非线性关系拟合出来，才能通过测量构型参数对残差值进行预测并补偿到测头坐标上，完成残差补偿。

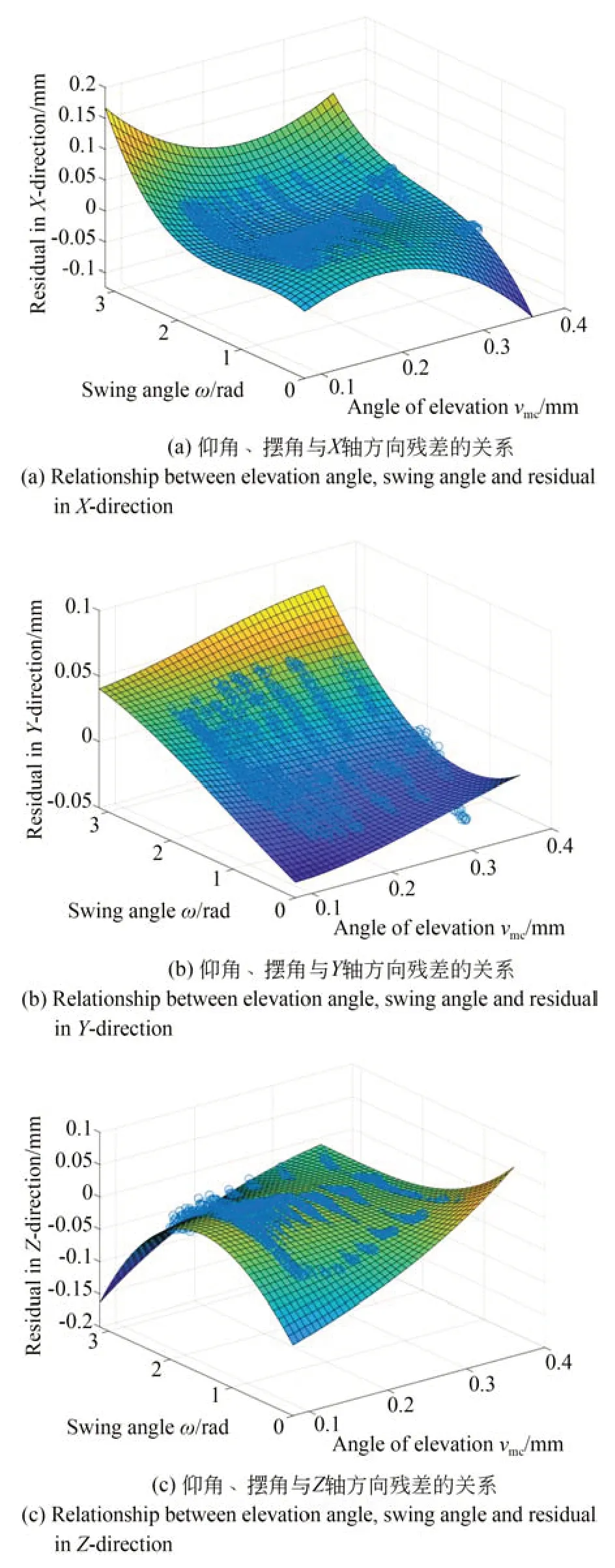
图11 仰角和摆角与残差的关系Fig.11 Relationship of the elevation angle， swing angle and residual

图12 长度和摆角与残差的关系Fig.12 Relationship of the length， swing angle and residual

3.2 基于ELM 的残差修正模型

3.1 节的分析表明测量构型与残差（Δx，Δy，Δz）之间存在着非线性映射关系，所以寻找测量构型参数与残差组成的非线性关系是残差补偿的关键。神经网络建模可以不需要了解内部具体结构，只需要具体的输入量和输出量经过一定的训练，便可准确地拟合出输入量和输出量之间的关系。神经网络的基本思想是隐藏层对输入矢量进行变换，将低维的输入数据变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。BP 神经网络、RBF 神经网络等神经网络常用于非线性函数的拟合。但BP神经网络和RBF 神经网络等的学习速度通常较慢，特别是当训练数据庞大时所消耗的时间成本高昂。极限学习机（Extreme Learning Machine，ELM）对前馈神经网络及其反向传播算法进行了改进，隐含层节点的权重为随机或人为给定的，且不需要更新，学习过程仅计算输出权重，只需要一次迭代即可完成，极大缩短了训练所需时间，具有较好的自适应性［29］。本文采用ELM 建立残余误差补偿模型。

将测量构型（ω，vmc，Lmc，θr）作为ELM 的输入参数，残差（Δx，Δy，Δz）作为输出量，建立ELM网络如图14 所示。

本文通过计算机编程实现ELM 算法，用于训练和保存ELM 网络，ELM 网络的具体计算步骤如下：

步骤1：确定ELM 网络的输入量（ω，vmc，Lmc，θr）和输出量（Δx，Δy，Δz），设置ELM 网络隐藏层节点数为300。

步骤2：随机生成ELM 网络的输入连接权重W，权值矩阵W的元素取［-1，1］之间的随机数。

步骤3：随机生成ELM 网络的隐藏层偏置矩阵b，偏置矩阵b的元素取［0，1］之间的随机数。

步骤4：Sigmoidal 函数具有平滑易于求导的优点，可以将低维特征映射到高维非线性空间中，是神经网络中常用的激活函数，本文确定以Sigmoidal 函数为激活函数。

步骤5：将实验采集计算得到的ELM 网络输出量和输入量带入到模型中，可求解ELM 网络的输出权重β。

步骤6：将连接权重W、和偏置矩阵b和输出权重β保存下来，即可完成ELM 网络训练。

步骤7：在进行测量工作时将实时计算的输入量（ω，vmc，Lmc，θr）代入到训练好的ELM 网络中计算输出量（Δx，Δy，Δz），并将其补偿到坐标值即可完成残差补偿：

其中（xnew1，ynew1，znew1）表示残差补偿后的测量坐标值。ELM 的训练流程和补偿过程如图15 所示。

4 实 验

单点重复精度是关节臂式坐标测量机的重复性的主要衡量指标。为了定义单点重复精度，首先定义以下几个参数。

坐标误差值：

坐标误差平均值：

坐标误差标准差σ：

其中：E代表所测数据的平均误差大小，σ代表误差的波动幅度，可以用E和σ组合来定义关节臂式坐标测量机的单点重复精度（Repeat Precision，RP）：

4.1 运动学标定实验

根据上述推导的数学模型，编写了关节臂式坐标测量机参数辨识和补偿软件。该软件基于C++和QT5.12 开发平台，具有数据采集、运动学标定和残差补偿的功能，图16 为软件界面截图。利用该软件采集了500 组关节角数据，将采集的数据导入事先写好的标定程序中，即可辨识得出标定后的运动学参数，如表2 所示。

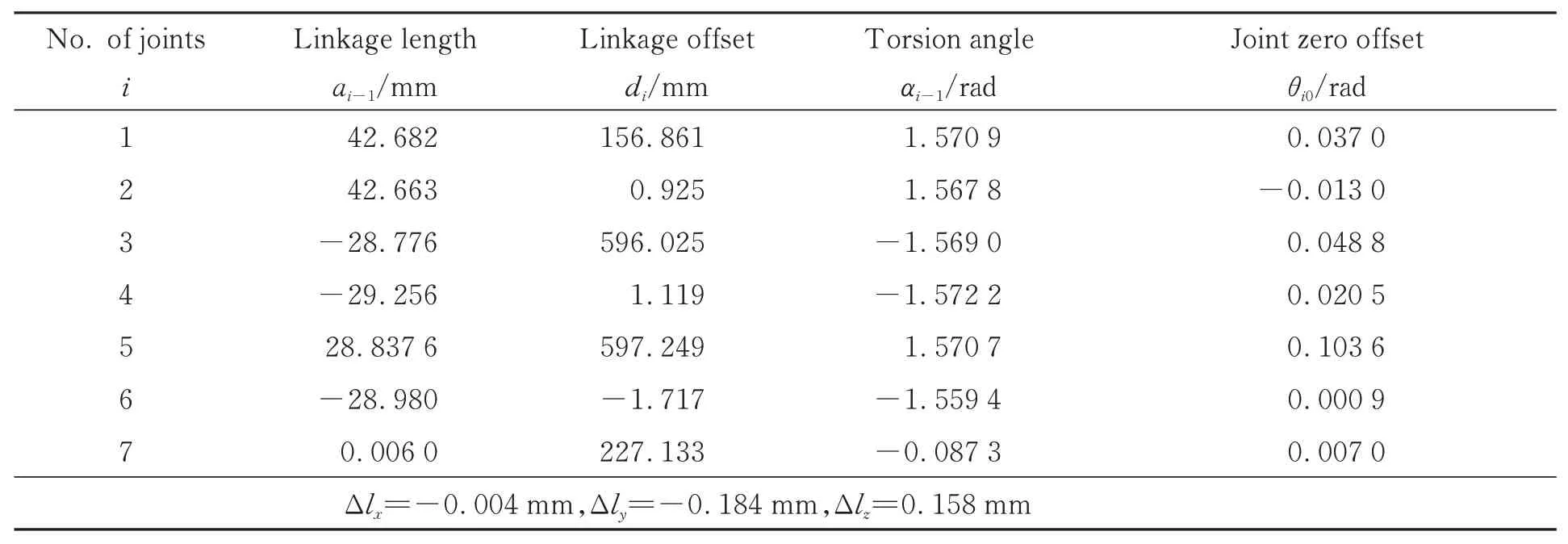
表2 D-H 参数标定后的值Tab.2 D-H parameter of the AACMM after identification

图16 标定补偿软件Fig.16 Calibration compensation software

为了验证运动学参数标定是否有效，需要采集数据进行验证。在工作台上采集了300 组数据进行验证，标定前关节臂式坐标测量机分量上的误差分布如图17 所示；标定后关节臂式坐标测分量上的误差分布如图18 所示。

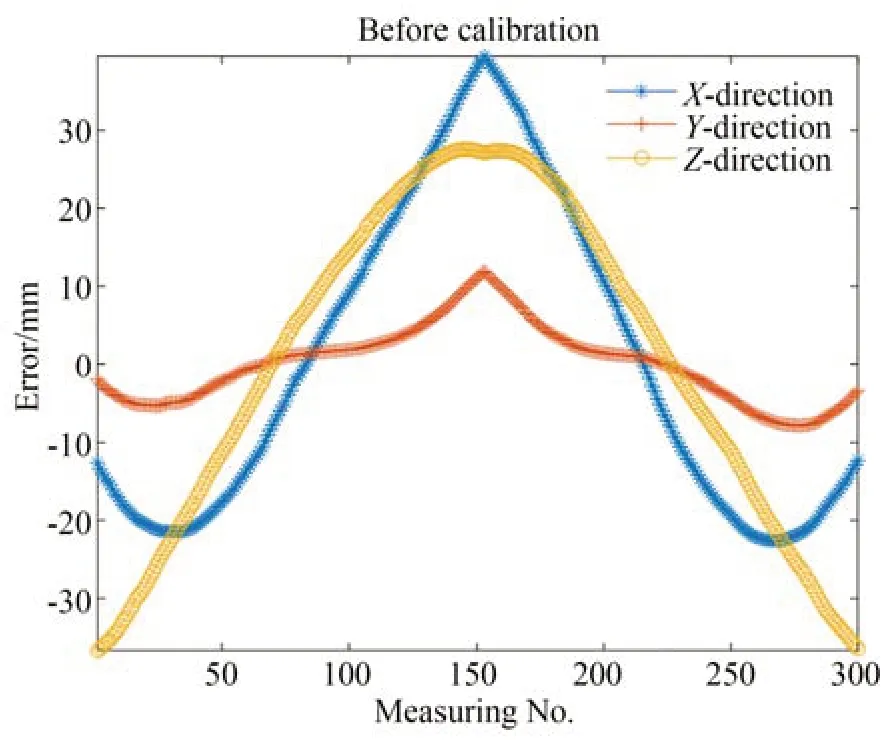
图17 运动学标定前的误差分布图Fig.17 Error distribution before calibration

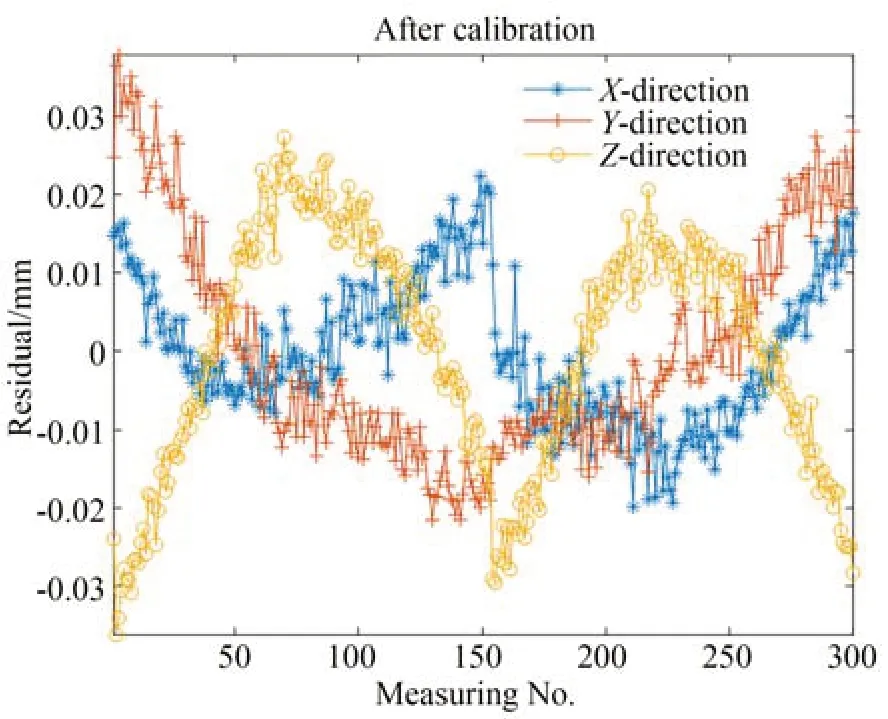
图18 运动学标定后的误差分布图Fig.18 Error distribution after calibration

具体数据如表3 所示，单点坐标误差的最大值、平均值、标准差由标定前的49.386 mm，26.498 mm，12.348 mm 下降到标定后的0.054 mm，0.021 mm，0.009 mm，表明所提复合标定法有效。

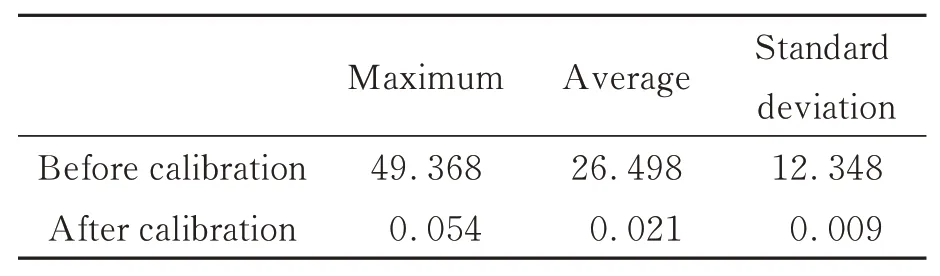
表3 复合运动学标定结果Tab.3 Compound kinematic calibration results （mm）

为了进一步验证复合标定法在测量空间中的泛化性。在空间随机采集了20 个点位的数据，每个点位采集300 组关节角，共计6 000 组数据。分别采用单点标定法和复合标定法标定后的模型计算重复误差，对比结果如图19 所示。关节臂式坐标测量机的单点坐标误差最大值和RP 由单点标定后的0.098 mm，0.084 mm 下降到复合标定后的0.061 mm，0.055 mm，实验结果表明复合标定法优于单点标定法，具体数据如表4所示。

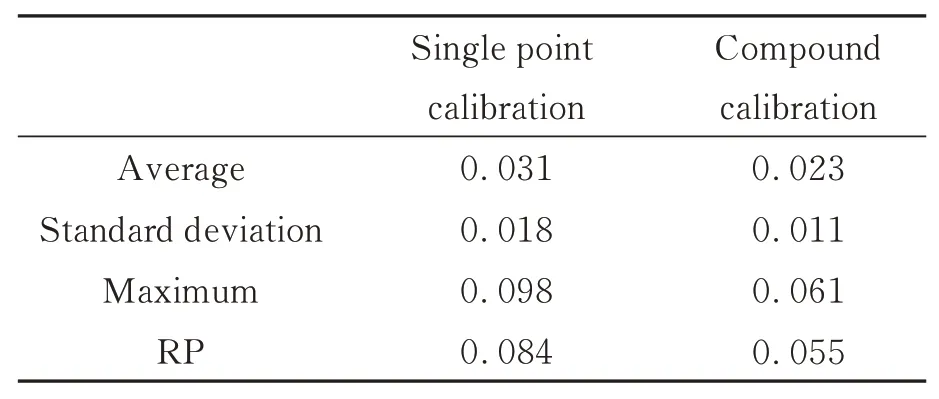
表4 运动学标定效果对比Tab.4 Comparison of kinematic calibration effects（mm）

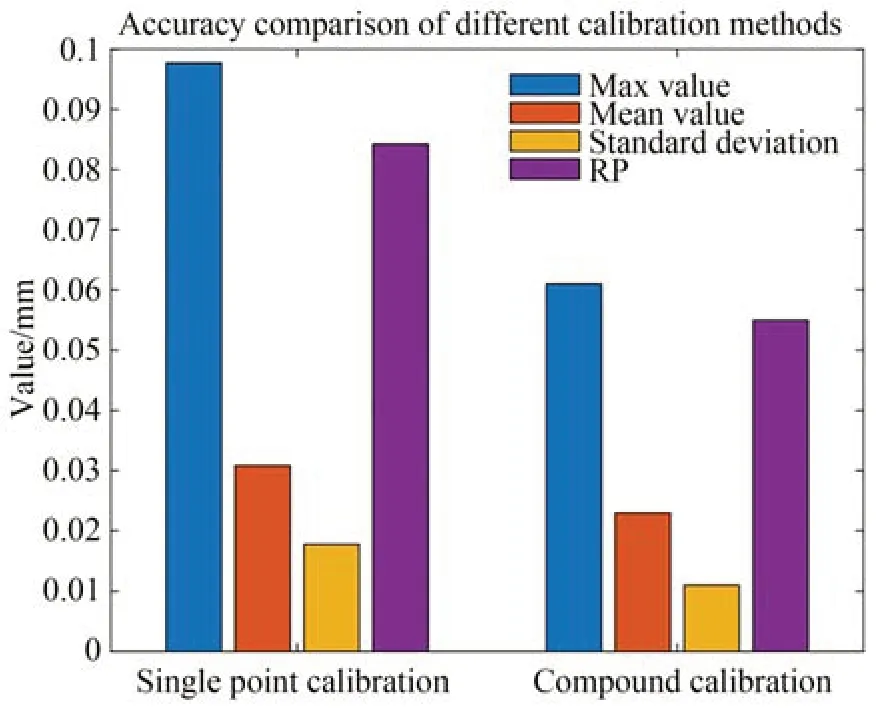
图19 运动学标定效果对比Fig.19 Comparison of kinematic calibration effects

4.2 残余误差补偿实验

在800 mm 长度范围内以40 mm 间隔，每个点位采集300 组不同测量构型下的关节角。完成数据采集后，计算相应的输入量（ω，vmc，Lmc，θr）和输出量（Δx，Δy，Δz）并导入ELM 模型中进行训练。当模型训练好后，将验证数据集计算出的输入量（ω，vmc，Lmc，θr）代入到训练好的ELM 模型中计算输出量，并补偿至坐标值中即可完成残差补偿。残差补偿效果如图20 所示，关节臂式坐标测量机的单点残差最大值和RP 由补偿前0.057 mm，0.057 mm 下降到补偿后的0.028 mm，0.032 mm，表明本文所提方法是有效的，具体数据如表5 所示。

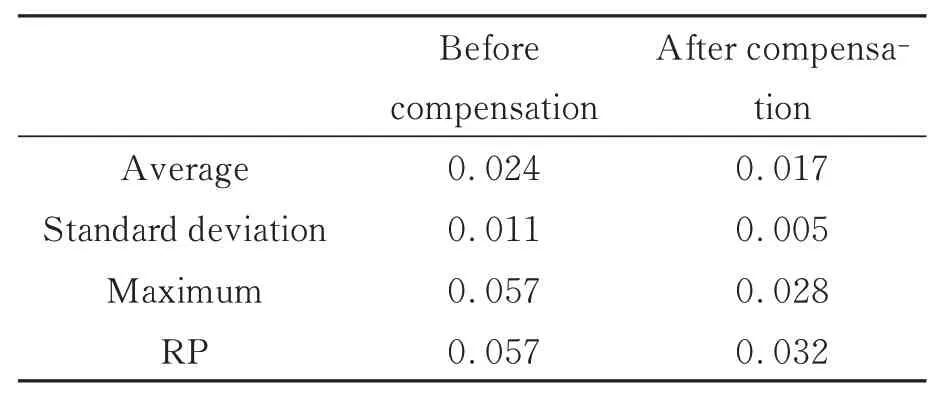
表5 残差补偿结果Tab.5 Residual compensation results （mm）

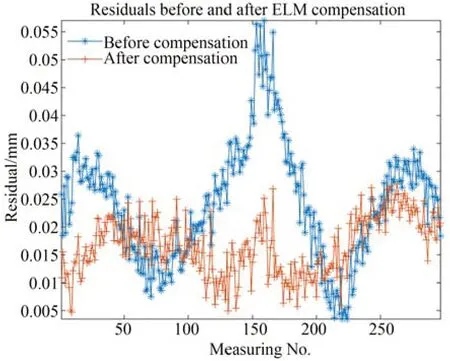
图20 残差补偿结果Fig.20 Residual compensation results

为了进一步验证所提方法在测量空间中的泛化性。在空间采集了20 个点位的数据，每个点位300 组关节角共计6 000 组数据。

首先完成了基于ELM 测量构型修正模型（MCCM-ELM）和基于BP 测量构型修正模型（MCCM-BP）的残差补偿对比实验。实验结果如图21 所示，MCCM-ELM 补偿后，残差的最大值和RP 由0.061 mm，0.055 mm 下降到0.044 mm，0.035 mm；MCCM-BP 补偿后，残差的最大值和RP 由0.061 mm，0.055 mm 下降到0.051 mm，0.043 mm，具体数据如表6 所示。实验结果表明，在补偿效果上MCCM-ELM 优于MCCMBP，并且ELM 训练时间为0.375 s、BPNN 的训练时间是17.874 s，所以MCCM-ELM 与MCCM-BP 相比而言具有补偿效果更好、训练效率更高的优点。

表6 不同拟合算法的残差补偿效果对比Tab.6 Comparison of residual compensation effects of different fitting algorithms（mm）

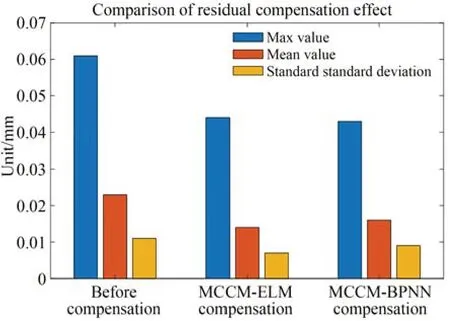
图21 不同拟合算法的残差补偿效果Fig.21 Residual compensation effect of different fitting algorithms

完成不同拟合算法的对比实验后，进一步完成了MCCM-ELM 和基于ELM 第五关节修正模型（FJCM-ELM）的残差补偿对比实验。

实验结果如图22 所示，FJCM-ELM 在进行泛化性验证实验时出现了一些补偿无效的点位，故MCCM-ELM 的泛化性优于FJCM-ELM，具体数据如表7 所示。综合上面两个对比实验可知，MCCM-ELM 具有泛化性更好、训练效率更高的优点。故本文最终选择MCCM-ELM 作为残差预测补偿的模型。

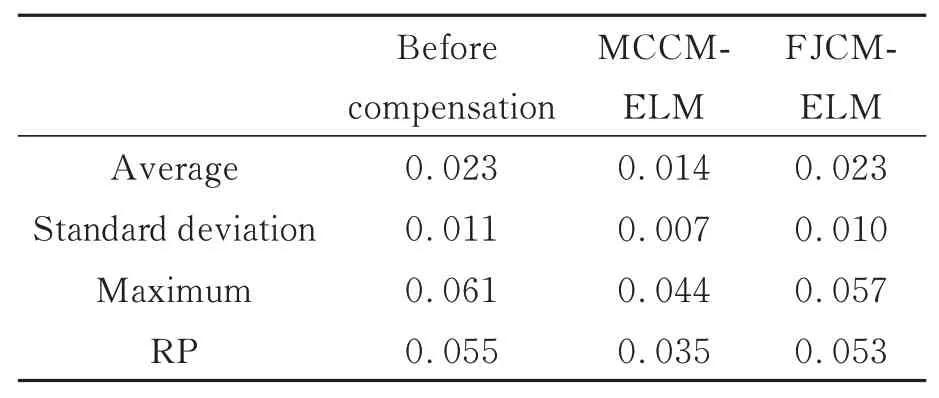
表7 不同残差补偿模型的补偿效果对比Tab.7 Comparison of compensation effects of different residual compensation models（mm）

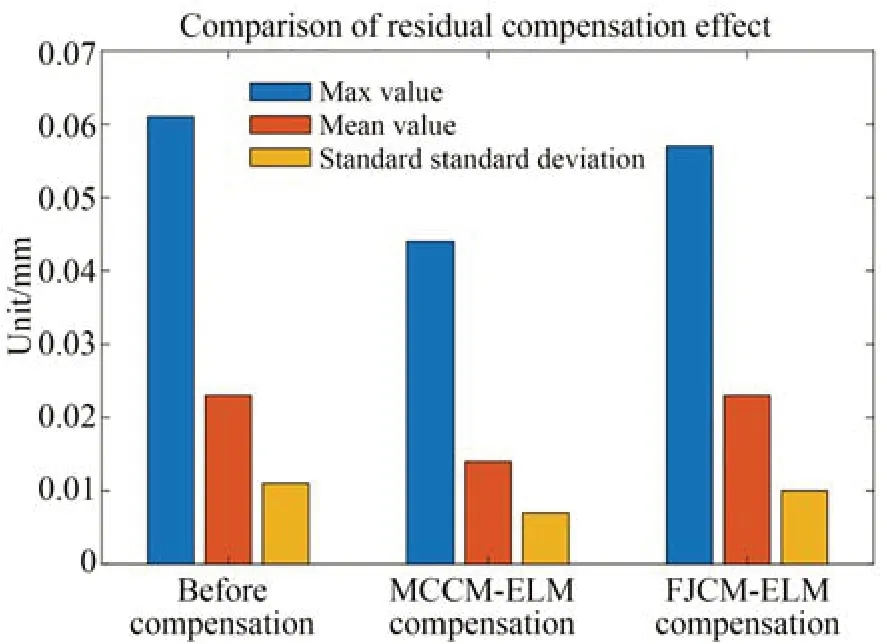
图22 不同残差补偿模型的补偿效果Fig.22 Compensation effect of different residual compensation models

由于残差补偿是针对单点进行补偿的，单点精度的提高只能表明重复精度的提高，下面对长度测量精度进行检验。使用300 mm 标准量块作为测量对象，分别使用残差补偿前后的坐标值对其进行120 次测量，其中100 组数据用来放缩长度参数、20 组数据作为验证集，验证结果如图23 所示。具体数据如表8 所示，长度测量误差的最大值、平均值、标准差由补偿前的0.137 mm，0.033 mm，0.037 mm 下降到补偿后的0.074 mm，0.021 mm，0.019 mm。上述实验结果表明本文所提方法不仅可以提高关节臂式坐标测量机的重复精度还可以提高其长度测量精度。

表8 标准量块测量结果Tab.8 Measurement results of standard gaug e （mm）

图23 标准量块测量结果Fig.23 Measurement results of standard gauge

5 结 论

本文以7 自由度关节臂式坐标测量机为对象，分析了其测量构型对残余误差影响的特性。构建了以测量摆角、仰角、距离和转角为变量的测量构型，在此基础上提出了基于ELM 的残差修正模型。单点精度对比测试实验结果表明：与只进行运动学标定相比，进行残差修正后关节臂式坐标测量机的坐标误差最大值下降27.9%、均值下降39.1%、标准差下降36.4%。同样地，长度测量实验结果表明：进行残差修正后关节臂式坐标测量机长度测量误差的最大值下降46.0%、均值下降36.4%、标准差下降48.6%。

实验中所用的7 自由度关节臂式坐标测量机结构和坐标变换模型具有通用性，因此所使用方法能便捷、有效地提高类似结构的关节臂式坐标测量机的单点重复精度，对关节臂式坐标测量机精度补偿具有一定参考意义。