基于改进引力搜索算法的高铁信号系统测试案例生成方法研究

史增树，李 耀，郭 进，张亚东

当前我国已成为世界上高铁运营里程最长、运输密度最高、运营场景最复杂的国家。信号系统是保障高铁安全、高效运行的核心，是典型的安全关键系统。如何高效生成覆盖全部测试需求的测试案例是高铁信号系统的重要研究内容［1-2］。

目前，对于高铁信号系统在测试案例生成方面的研究主要基于模型的测试理论，包含抽象测试案例生成和抽象测试案例实例化为具体测试案例等。如针对列控系统测试，文献［3-5］ 研究基于UML模型的测试案例生成方法；文献［6］结合混合通信顺序进程和时间自动机模型，研究测试案例自动生成问题；文献［7-8］将时间自动机理论和变异测试技术相结合，提出列控系统安全功能测试案例生成技术；针对车载设备逻辑复杂的特点，文献［9-10］提出基于SCADE 模型的测试案例生成方法；文献［11-12］基于UPPAAL Cover 工具，研究基于自动机模型的测试案例生成技术；文献［13］提出基于Colored Petri Net 模型的测试案例生成方法。以上研究重点关注抽象测试案例的全面性和重复度。

在抽象测试案例实例化为具体测试案例方面，文献［14］针对列控系统抽象测试案例实例化的问题，基于确定性有限状态机模型，提出输入空间划分和逻辑覆盖相结合的抽象测试案例自动实例化方法；文献［15］以CTCS-3级列控系统等级转换场景为例，研究基于时间自动机模型的抽象测试案例生成方法，进一步提出基于排列组合的具体测试案例生成流程；文献［16］从组合测试的角度，基于有限状态机模型研究信号系统具体测试案例的实例化方法。

高铁信号系统抽象测试案例实例化时，测试项可能包括多个实例化取值，导致具体测试案例的数量庞大。如何将抽象测试案例实例化为高效的具体测试案例是高铁信号系统测试中的重要问题，目前的研究尚未深入地对该问题展开探讨。为此，本文基于有限状态机建模方法，引入并改进引力搜索算法，对信号系统抽象测试案例实例化为具体测试案例的过程进行研究，在保证具体测试案例全面性的同时，降低测试案例的数量，对降低高铁信号系统测试成本具有一定的意义。

1 高铁信号系统测试案例生成过程

高铁信号系统测试案例生成过程见图1。基于模型的测试是高铁信号系统测试的重要研究方向，主要包括系统需求分析、测试模型建立、抽象测试案例生成、抽象测试案例实例化、测试执行和测试结果分析6 个阶段。首先，基于信号系统的需求规格等文件对系统功能进行抽象，建立系统的测试模型；其次，依据测试模型，选取测试覆盖准则，自动生成抽象测试案例；然后结合行业知识，将抽象测试案例实例化为可执行的具体测试案例；最后，将具体测试案例加载到测试环境中执行测试，观察、分析测试结果。

图1 高铁信号系统测试案例生成过程

在将抽象测试案例实例化为具体测试案例的过程中，抽象测试案例可能包括多个实例化取值，如抽象测试案例“开放允许信号”，实例化的具体测试案例可能为L 码、LU 码等。在生成具体测试案例时，需要覆盖每个实例化取值。在如图2 所示的有限状态机（Finite State Machine，FSM）［17-18］测试模型中，s0为初始状态，sf为终止状态，g1~g5为转移；g1~g4有1个实例化取值，g5有2个实例化取值。模型存在3条抽象测试案例p1、p2、p3：

图2 FSM模型

为覆盖g5的2 个实例化取值，生成具体测试案例时，可以分配p2中g5取值z5，p3中g5取值z6，即模型通过3 条具体测试案例T1、T2、T3，覆盖抽象测试案例和所有的实例化取值：

通常，铁路信号系统抽象测试案例的实例化取值较多。文献［16］对ZPW-2000轨道电路接收器进行了研究，其抽象测试案例“电压无效”包括20个实例化取值，“频率无效”包括24个实例化取值。信号系统测试需要覆盖所有的抽象测试案例和全部的实例化值；同时，为节省测试资源，应当使测试成本（消耗的资源、时间等）尽量较低，具体要求如下。

1）覆盖所有抽象测试案例，即每个抽象测试案例至少需要测试1次。

2）覆盖所有的实例化值，即每一个实例化取值至少被一条具体测试案例覆盖。

3）总体测试成本较低。信号系统测试繁琐复杂，将实例化值合理分配到抽象测试案例，能够有效降低具体测试案例的数量，减少系统的测试成本。

综上，高铁信号系统抽象测试案例的实例化过程存在一个典型的优化问题：如何在保证100%覆盖抽象测试案例和实例化取值的前提下，总体测试成本控制较低，即：

式中：n为测试模型转移的数量；C(gi)为转移gi的测试成本；E(gi)为转移gi实例化取值的数量；K(gi) 为转移gi实际的执行次数。

2 基于引力搜索算法的测试案例生成方法

结合FSM提出基于引力搜索算法的高铁信号系统测试案例生成方法［19］，见图3，具体步骤如下。

图3 基于改进引力搜索算法的测试案例生成方法

Step 1采用FSM描述高铁信号系统的测试需求，建立FSM测试模型。

Step 2利用FSM测试案例生成算法自动生成高铁信号系统的抽象测试案例。

Step 3根据测试需求，提取FSM模型中各个转移的实例化取值，计算抽象测试案例的测试成本。

Step 4克服算法早熟的缺点，综合高铁信号系统抽象测试案例、实例化取值和测试成本3 个因素进行搜索，生成具体化的测试案例。

2.1 引力搜索算法

2009 年，Esmat Rashedi 等学者结合万有引力定律，提出了一种新型的群体智能优化算法——引力搜索算法（Gravitational Search Algorithm，GSA）。研究发现，该算法具有较强的全局搜索能力，在标准测试函数优化试验中，寻优精度和收敛速度都明显优于粒子群优化算法（PSO）和遗传算法（GA）［20］。

引力搜索算法首先在解空间和速度空间分别对位置和速度进行初始化，然后评价各个个体的目标函数值，确定每个个体的质量和受到的引力，计算加速度，更新速度和位置。

2.1.1计算质量

对N个个体，个体i的质量Mi( )

t定义为式中：fiti(t)为第t次迭代个体i的适应度函数值；best(t)和worst(t)为在第t次迭代时，所有个体中最优的适应度函数值和最差的适应度函数值。

2.1.2计算引力

在第d维上，个体j对个体i的引力定义为

式中：G(t) 为在第t次迭代时的万有引力常数；Rij(t)为个体i和j之间的欧氏距离，i，j∈{1，2，…，N}，且i≠j，d=1，2，…；ε为防止分母为零的常数；分别为个体i、j在第d维的位置分量。

式中：G0和a为常数，T为最大迭代次数。

在第d维上，个体i所受的合力为

式中：randj为在[0， 1]之间服从均匀分布的随机变量；kbest为个体质量按降序排在前k个的个体，且k的取值随迭代次数线性减小，初值为N，终值为1。

2.1.3计算加速度

个体i在第d维的加速度方程为

2.1.4更新速度和位置

式中：u为在[0， 1]之间服从均匀分布的一个随机变量。

2.2 基于改进引力搜索算法的测试案例生成

对于FSM 测试模型，其包含的转移集合记为Γ={g1，g2，…，gn}，转移实例化取值数量记为E={E(g1)，E(g2)，…，E(gn)}，抽象测试案例集记为P，p∈P的测试成本记为C（p）。对于图2 所示的FSM 模型，Γ={g1，g2，g3，g4，g5}，E(g5)=2，P={p1，p2，p3}，假设g1，g2，g3，g4，g5的测试成本分别为10，30，50，20，20，则C(p1)=60，C(p2)=50，C(p3)=50。

抽象测试案例实例化问题可转化为计算FSM模型抽象测试案例的执行次数，使其在实例化时能够全面覆盖抽象测试案例所有的实例化取值，且测试成本较低。引力搜索算法在测试成本{C(p1)，C(p2)，…，C(pn)}的约束下，根据抽象测试案例包含的各个转移实例化取值数量，搜索抽象测试案例的执行次数。由于需要对抽象测试案例至少覆盖1 次，则x(t)下转移gi的执行次数记为Kx(t)(gi)，则抽象测试案例实例化过程的适应度函数fit(t)为

迭代过程中，所有个体最优适应度函数值best(t)和最差适应度函数值worst(t)定义为

由于传统的引力搜索算法存在局部收敛，导致早熟的问题［21］，因此需进行改进，引入遗传算法中应用较好的最优保存策略［22-23］，并加入末位淘汰机制。即：每次算法迭代后，如果某个体优于当前最优个体，则保持该个体的当前位置，淘汰适应度最差的个体，即将适应度最差的个体重新初始化到解空间，将所有个体迭代次数重置为0。

基于改进引力搜索算法的测试案例生成流程见图4，包括以下阶段：

图4 基于改进引力搜索算法的测试案例生成流程

Step 1随机初始化所有个体的位置，每个个体的初始速度为零。

Step 2计算每个个体的适应度函数值。

Step 3利用式（2）、（5）、（11）、（12）分别更新M（t）、G（t）、best（t）、worst（t）。

Step 4利用式（6）计算每个个体受到的引力。

Step 5利用式（4）、（6）、（7）计算每个个体的加速度。

Step 6利用式（8）、（9）更新每个个体的速度和位置。

Step 7根据优化规则，更新个体位置和迭代次数。

Step 8重复步骤Step 2~Step 8，直到满足终止条件。

Step 9输出当前结果并终止算法。

3 案例分析

以高铁信号系统中CTCS-2级向CTCS-3级转换的功能为例，介绍测试案例生成过程。

3.1 等级转换功能抽象测试案例生成

在CTCS-2级向CTCS-3级转换前，需要完成的工作包括：车载电台注册到GSM-R 网络、车载设备与RBC 建立通信会话、车载设备从RBC 获得系统配置参数和行车许可等信息。如果在转换边界不具备CTCS-3 级控车条件，列车将继续按CTCS-2级运行，直至CTCS-3级控车条件具备后，车载设备将自动转入CTCS-3级工作。转换过程中，可能出现的异常情况包括：呼叫RBC不成功、取消等级转换、未同时得到等级转换命令和MA、转换时超过CTCS-3级允许速度、未收到等级转换应答器组消息。

为了在不同运行速度下对等级转换功能的执行情况进行测试，将转换过程中的速度等级划分为高速（大于250 km/h）、正常速度（100~250 km/h）和低速（小于100 km/h）3 种模式，FSM 测试模型及转移的实例化取值测试见图5。

图5 CTCS-2级向CTCS-3级转换FSM测试模型

图5中，E（g2）=2，E（g20）=3，E（g21）=3，E（g17）=5，E（g18）=5，E（g16）=7，其余转移的实例化取值数量均为1。如g17表示列车以正常速度通过执行应答器，正常速度（单位为km/h）的实例化取值范围包括：（0，100），［100，150），［150，250），［250，300），［300，350］，分别取不同范围下的速度通过执行应答器进行测试。

对于测试模型，采用文献［19］提出的测试案例生成方法，生成24条抽象测试案例，见表1。以测试人员准备车载设备上电的时间为测试成本的基础标准，记为S。每条抽象测试案例的测试成本由测试人员根据工程测试数据，结合测试经验进行确定。为描述方便，抽象测试案例仅保留FSM 测试模型中的关键转移。以抽象测试案例p6为例，测试内容为：列车以CTCS-2 级运行，检测到GSM-R 网络唯一，连接GSM-R 网络和RBC 成功后，检测到等级转换预告应答器，但未同时得到等级转换命令和MA，保持CTCS-2级工作状态进入CTCS-3 级区域后，未收到RBC发送的MA 和线路描述信息，转为CTCS-3 级后，执行冒进防护。

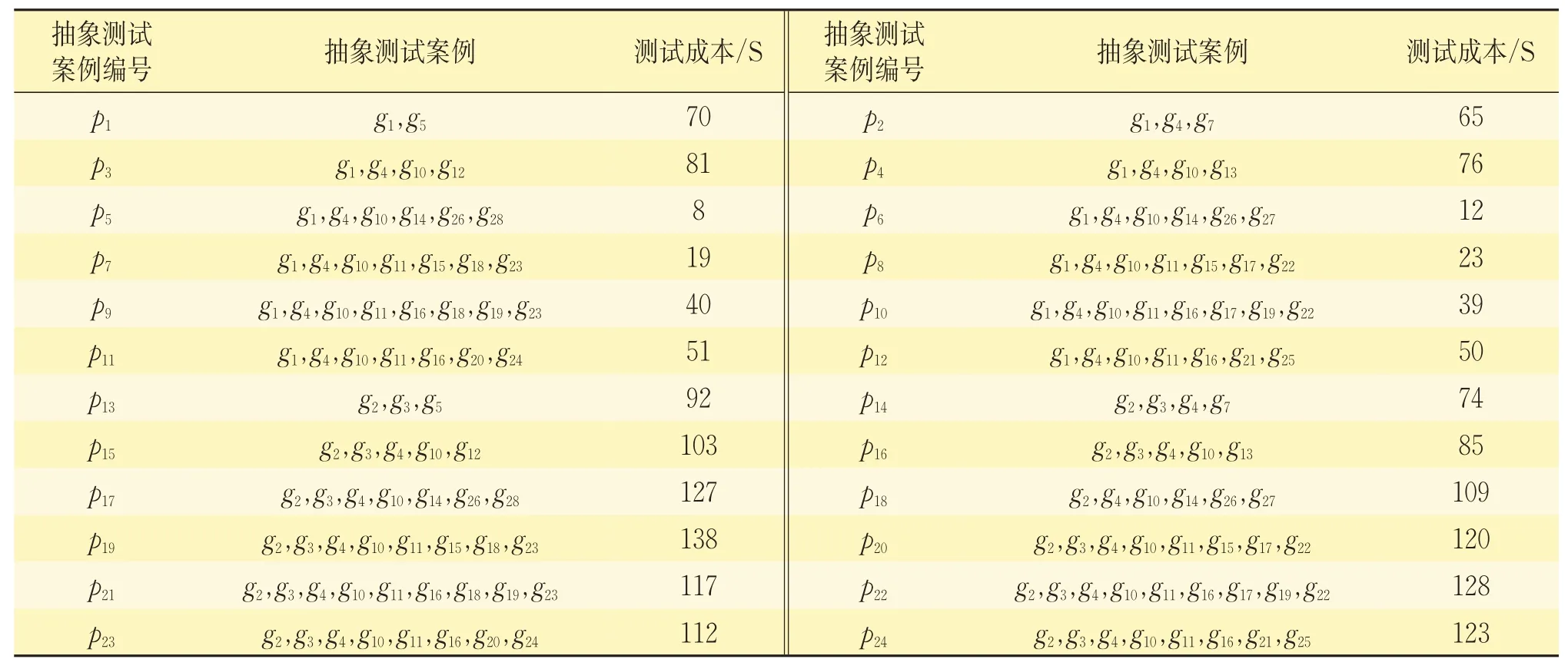
表1 抽象测试案例及测试成本

3.2 等级转换功能具体测试案例生成

改进的引力搜索算法的个体数设定为50，G为5，迭代次数为200。在第137次迭代后，测试总成本达到最小2 005，共计28 条具体测试案例，测试案例覆盖的实例化取值信息见表2。由于p1~p6各个转移的实例化取值唯一，对应的具体测试案例唯一，为节省篇幅，表2未列举。

表2 等级转换主要的具体测试案例

由表2可知，抽象测试案例p7、p8、p11、p12分别需要测试2次。如p7，其具体化测试案例分别为T1和T3，实例化取值分别为［150，250）和（0，100）。

为验证改进引力搜索算法的性能优化效果，图6 给出了与基于传统的引力搜索算法测试案例生成方法的比较曲线。在传统的引力搜索算法中，个体数设定为50，G为5，迭代次数为350。第124次迭代时，测试总成本达到最小2 412；而改进的引力搜索算法获得的测试总成本更低，克服了引力搜索算法容易出现早熟的问题。

图6 测试案例生成对比

4 结论

本文提出一种高铁信号系统测试案例生成方法，重点对抽象测试案例实例化为具体测试案例的关键问题展开了研究。从FSM 测试模型生成抽象测试案例，采用改进引力搜索算法对抽象测试案例实例化取值及测试成本进行优化，生成覆盖全面且测试成本较低的具体测试案例。以信号系统中的等级转换功能为例进行了案例分析，结果表明该方法能够满足信号系统的测试需求。下一步，将继续对实例化取值之间的组合问题展开研究。