FPGA 平台上基于PUF 的随机数产生技术*

唐六华，李赛野，孙夏声

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引言

随机数是一种无规律的数字序列，具有不可预测性和唯一性，被广泛应用于密码、安全等领域。但传统的随机数产生技术存在一些问题，例如：伪随机发生器（Pseudo Random Number Generator，PRNG）存在周期性可预测的弱点，无法满足一些场景的需求；采用专用的随机数产生芯片会增加硬件的体积、功耗和成本。因此，本文将物理不可克隆函数（Physical Unclonable Function，PUF）技术引入到现有的通用器件现场可编程门阵列（Field Programmable Gate Array，FPGA）中生成随机数，可以在不增加额外器件（如随机数芯片）的情况下提供更高质量的随机数。

1 基于FPGA 的PUF 技术原理

1.1 PUF 技术简介

PUF 是指对一个物理实体输入一个激励，利用其不可避免的内在物理构造的随机差异输出一个不可预测的响应。这些响应具有唯一性和不可复制性等特点。

近些年来，PUF 作为一种新兴的技术，因其唯一性和不可复制的物理特性被应用在身份认证、防篡改、密钥管理等领域[1]。同时，PUF 技术输出的响应也具有一定的不确定性，其每次输出的响应并不完全一致且存在一定的噪声，利用这种噪声，原理上可以产生真随机数。

1.2 基于FPGA 的PUF 实现原理

基于FPGA 的PUF 技术为环形振荡器（Ring Oscillator，RO）PUF[2]，下文简称RO-PUF。环形振荡器为FPGA 中的常用电路，它由多个反相放大器组成，如图1 所示。当电路启动时，由于反向器的增益，电路会产生自激荡，产生一个连续的周期信号输出，可用于产生时钟。由于制造差异的影响，数字信号的传播延迟将会有部分随机性，FPGA 中不同的RO 会有不同的频率输出。

图1 环形振荡器结构

基于RO 产生频率不同的这种特点，RO-PUF主要由环形振荡器阵列、计数器和比较器3 部分构成[3]，具体结构如图2 所示。首先使用计数器统计一定时间内环形振荡器振荡的次数；其次将统计结果输入到比较器进行比较，产生0 或者1 的响应。

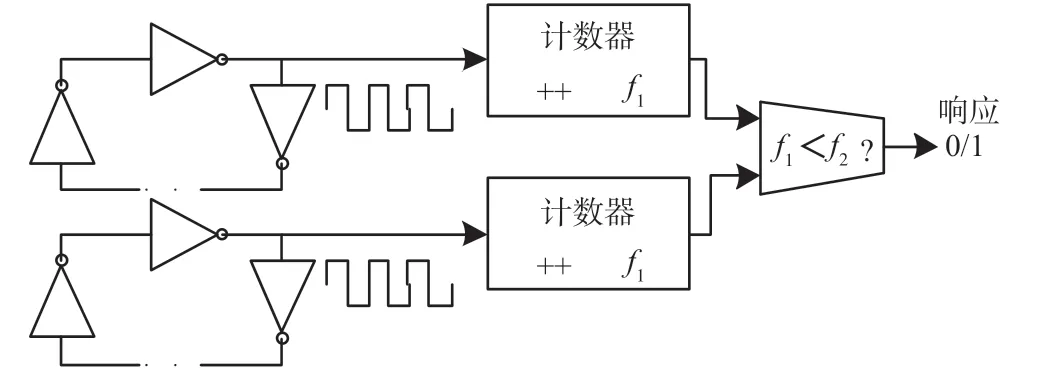
图2 环形振荡器PUF 结构

RO-PUF 单元大多数时候具有稳定的响应值，而部分RO-PUF 单元输出响应不是固定值，具有一定噪声。在PUF 技术的应用中，通常把RO-PUF输出响应值作为特征值。本文将特征值中不稳定的单元作为随机数产生的熵源。

2 PUF 随机数产生技术

2.1 基于FPGA PUF 的随机数产生原理

本文研究一种基于FPGA PUF 的随机数产生技术，该技术主要利用FPGA 中部分RO PUF 单元输出数据的不稳定性，引入随机数池、压缩算法等技术实现随机数序列发生器，基本原理如图3 所示。

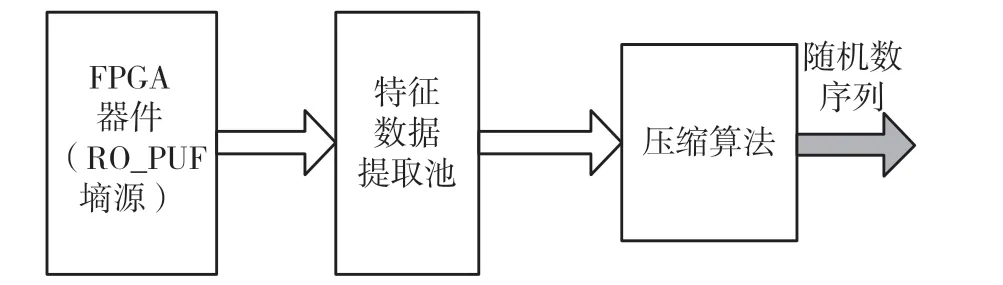
图3 基于PUF 的随机数产生实现结构

该结构主要包括熵源、特征数据提取池和压缩算法3 个部分。

（1）熵源：部分RO-PUF 输出的未知状态，为噪声的来源。

（2）特征数据提取池：提取RO-PUF 阵列的特征值存储到该特征池中。

（3）压缩算法：其目的是把特征值池中的数据进一步压缩转化，最终输出全熵的随机数序列。

通过这种结构可以不断提取RO-PUF 的输出值，并将输出值保存到特征值提取池中，当获取到一定数量的数据后，将特征值池中的数据导入到后续的压缩算法，对数据进行压缩，获取更高熵值的随机数。

2.2 基于RO-PUF 的随机数发生器设计

基于PUF 的随机数发生器需要大量的输出数据作为熵源，经研究使用RO PUF 可以满足其对输出特征数量的需求[4]。整个系统总体结构共包括RO阵列、计数器组、比较器组、特征值池、压缩模块、通信模块这6 个模块，具体如图4 所示。

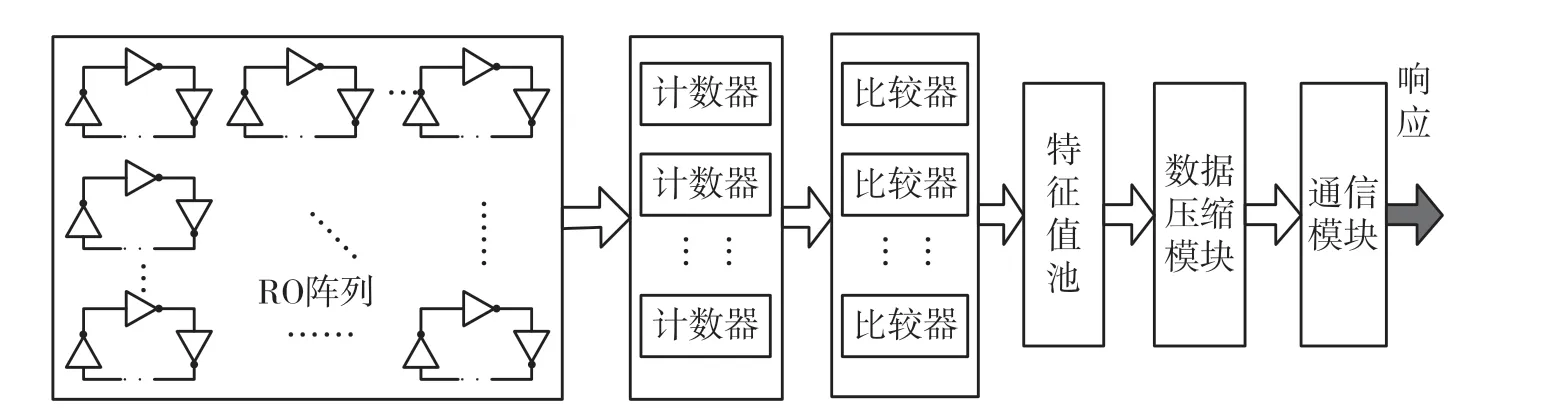
图4 RO-PUF 的随机数产生设计

本文采用Xilinx K7 325T FPGA 进行设计，在FPGA 中进行布局、布线实现1 024 个RO PUF 单元，一次采样周期可以输出1 024 bit的原始特征值数据，其FPGA 内部结构如图5 所示，随机数获取界面如图6 所示。

图5 RO-PUF 的随机数产生设计结构

图6 RO-PUF 的随机数获取界面

3 PUF 技术的随机数产生性能

3.1 RO-PUF 误码率熵值分析

对基于FPGA 的RO-PUF 进行高低温测试，实验条件为温度从-30 ℃提升到65 ℃，每提升10 ℃保持1 h，在不同温度下对RO-PUF 输出响应进行100 次采集和对比，计算其中的误码率（Bit Error Ratio，BER）即噪声，计算公式如下：

式中：Ri和Rj表示同一温度下第i次采集的响应数据和第j次采集的响应数据，HD(Ri,Rj)表示两次采集响应数据之间的汉明距离，N表示测试总数，l表示单次测试响应数据位宽。通过该计算公式可以求得不同温度下采集数据的噪声，测试结果如图7所示。

图7 RO-PUF 的随机数获取界面

根据试验得出基于该款FPGA 实现的RO-PUF在温度越低的情况下噪声越大，随着温度的升高逐渐稳定。

3.2 RO-PUF 误码率熵值分析

在信息论中，熵用来表示对某件事的不确定性的度量。熵值越大表示随机性越大，所获得的信息量越少；熵值越小表示随机性越小，所获得的信息量越多，体系结构越规则。因此，为了提取高质量真随机数，需要获得高熵值。其中，最小熵表示最坏的不确定性大小，根据误码率计算最小熵的公式如下[5]：

对于n个bit 的最小熵计算公式如下[5]：

数据压缩算法采用Hash 函数，因为Hash 函数本身就是strong extractor[6]，其输出在{0,1}上均匀分布。可以利用一个Hash 函数作为熵累加器，从熵值较低的低质量随机数中提取定长的熵值较高的高质量随机数。本文采用SM3 密码杂凑算法[7]作为熵累加器。

根据Hash 函数的特性，假设需要提取256 bit的随机序列，则至少拥有510 bit 的最小熵值[8]。

综上，获取长度为Y的随机序列至少需要计算前数据长度约为2Y[8]的最小熵值。对于提取长度为Z的随机数序列，需要的特征池数据长度L的计算公式为：

根据式（4），对于一个BER为10%的PUF输出响应，L≥45×Z。

3.3 RO-PUF 产生随机数的速率

RO-PUF 模块依托Xilinx K7 325t FPGA 平台，采用5 阶环形振荡器设计[9]，并采用RGMII 接口进行通信。如图8 所示其中随机数的产生速率主要由以下几个关键部分组成。

（1）计数器数计算时间。本文RO-PUF 计数器计算100 次进行输出，RO-PUF 产生的时钟约为5 MHz，数据输出延时为2 μm。

（2）数据压缩时间。本文采用Hash 算法为SM3 算法在FPGA 中实现，根据3.2 节的分析，在BER为10%时，对一组12 288 bit 的PUF 响应数据进行压缩可以得到256 bit 高质量随机数，SM3 算法在FPGA 实现输入到输出的时钟周期约为1 024 个，FPGA SM3 工作时钟为100 MHz，输入数据位宽为1 024 bit，输出杂凑值位宽为256 bit，产生的数据延迟为120 μm。

综上，数据延迟合计为122 μm，随机数产生速率约为2 Mbit/s。

3.4 RO-PUF 产生随机数性能

随机数产生器产生的输出需要进行统计分析和随机性测试以判断序列的好坏，目前国内外存在多种评估标准，目的是测试由随机数产生器产生的二进制序列的随机性，其中业内主要进行频数、序偶、扑克、自相关、游程检验[10]共5 项检测，每一项测试显著水平为0.01。

本文对PUF 技术输出的随机数进行采样，并提取10 Mbit的随机数数据进行检测，经测试满足频数、基偶、自相关、游程检测，显著水平为0.01。

4 PUF 产生随机数的应用探讨

4.1 RO-PUF 随机数应用优缺点

基于PUF 技术的随机数产生方案相对于传统的伪随机数发生器在随机性方面具有天然的优势。该方案基于FPGA 中RO 的物理特性的微小差异产生随机数，确保了产生随机数的随机性和不可预测性，解决了采用伪随机数发生器产生随机数面临的可预测性和易受攻击性等问题。

然而，PUF 技术产生的随机数也有一些固有的缺点，其输出容易受到环境和工作条件的影响，这导致PUF 技术生成的随机数质量下降。此外，本文提出的基于FPGA PUF 的随机数产生技术依托于FPGA 器件，需要硬件设备具备一定条件，但其相对于采用噪声源芯片具有更高的灵活性。

综上，基于FPGA PUF 技术的随机数产生技术相较于传统的伪随机数发生器具有随机性、抗攻击性等优点，相较于噪声源芯片具有更高的灵活性，但也面临不确定性和设备依赖性的问题。

4.2 FPGA PUF 环境适应性分析

通过第3 节的实验统计分析可以得到，温度的变化对基于FPGA 的PUF 的稳定性有一定的影响，低温下的稳定性均低于高温状态。

综上，在温度升高的情况下，PUF 技术产生的特征值较为稳定；在温度降低时，PUF 技术产生的特征值稳定性逐渐降低，出现更大的随机性，更适用于随机数产生业务。

5 结语

在密码领域的发展中，随机数一直是一个关键的研究方向，其在密码学中的应用越来越重要。其中，PUF 技术作为一种新兴技术可以利用其器件的微小差异的随机性来生成不可复制的序列，这使得PUF 技术在生成高质量随机数方面具有巨大前景。本文对PUF 技术在随机数方面的应用进行了研究，分析了PUF 技术的原理，提出了PUF 技术在FPGA中产生随机数的应用模式，并根据PUF 技术的特点设计引入特征值池、压缩算法等技术实现了随机数发生器。经过测试表明，常温下该设计满足随机数检测，可以提供比伪随机数更优越的随机性。此外，该设计通过通用器件FPGA 进行实现，对比基于噪声源芯片的方法具有更高的灵活性。