火箭分离与姿控一体化设计方法研究

缪 佶，孙晓娜，陈之润，汪庆雷

（北京宇航系统工程研究所，北京，100076）

0 引言

火箭在执行飞行任务过程中需要经历多个分离环节，其分离过程是一个复杂的高速多体运动过程，涉及空气动力学、多体动力学、理论力学、飞行力学、姿态控制等多个学科专业［1］。由于分离涉及学科广泛、运动过程复杂，火箭/导弹飞行任务失利往往由分离问题导致，故分离设计是火箭/导弹方案设计中至关重要的一环。

对于头体分离，上面级构型非轴对称的火箭气动特性较复杂，且该型火箭往往在低空高速环境下分离，分离动压相对较大，分离过程中上、下面级容易产生明显相对姿态转动，导致碰撞干涉风险增大［2］，因此在分离过程中对分离体进行实时姿态控制可以有效提升分离的可靠性［3］。

分离仿真是分离设计中十分重要的技术手段，其实质是求解由多个刚体组成的多体动力学数学模型。经过多年的发展，分离仿真技术已逐渐从自编程发展至数字样机模拟仿真，从二维三自由度仿真发展至三维六自由度仿真，从单一学科仿真发展至多学科耦合仿真［4］。随着分离仿真技术不断进步、仿真计算精度不断提高，开展分离与姿控联合仿真能够充分分析姿态控制力对两体安全分离起到的有利影响，并对分离体相对运动情况进行精确预示。因此，对于分离环境恶劣、相对运动过程复杂、分离难度大的火箭头体分离问题，开展分离与姿控一体化设计研究十分必要［5］。

1 分离与姿控一体化设计方法

1.1 分离动力学与姿控数学模型

将分离体视为刚体，并在分离过程中考虑姿控对分离后体的影响，建立分离动力学数学模型。在火箭设计中，头体分离的动力学方程一般通过牛顿-欧拉矢量力学推导获得［6］，其中分离前体质心平动的动力学方程组为

分离后体质心平动的动力学方程组为

式中 下标为1的参数均与分离前体相关；下标为2的参数均与分离后体相关。X，Y，Z分别为分离体在速度坐标系下受到的气动阻力、升力、侧向力；P为分离后体在分离过程中受到的后效推力，后效推力随分离时间变化；Fx，Fy，Fz分别为分离后体的控制力在三方向上的分量；m为分离体质量；V为分离体速度；θ为弹道倾角；φv为弹道偏角；α为攻角；β为侧滑角；γv为速度滚转角。

分离前体绕质心转动的动力学方程组为

分离后体绕质心转动的动力学方程组为

式中Jx，Jy，Jz为分离体绕弹体系三轴的转动惯量；ωx，ωy，ωz为分离体相对质心的旋转角速率；Mx，My，Mz为分离体受到的气动力矩在三方向上的分量；Mcx，Mcy，Mcz为分离后体受到的控制力矩在三方向上的分量。

对式（1）～（4）进行联合求解即可实现分离动力学与姿态控制的耦合计算，从而获得姿态控制下，上、下面级的质心运动和姿态转动情况。

1.2 分离与姿控联合仿真

分离与姿控联合仿真涉及多体动力学分析模型建立和姿态控制律设计两个方面，并须完成输入输出接口设置，在仿真的每一迭代步进行数据交换。具体的联合仿真方法描述如下，联合仿真流程如图1所示。

a）首先使用CAD三维建模软件建立精确的分离前体和分离后体几何模型，确保分离易碰撞点位置和分离间隙准确；

b）将创建好的三维模型导入多体动力学仿真软件中，基于实际分离工况设置分离体间的约束关系、测量状态变量、传感器和驱动，建立精确的多体动力学分析模型；

c）以分离过程中分离前体和分离后体不发生碰撞为目标，完成分离体的姿态控制律设计；

d）将姿态控制律并入多体动力学分析模型，完成分离/姿控一体化仿真平台构建，在仿真过程中根据每一迭代步前、后体相对位置和姿态输出姿控指令。

以上步骤完成后即可获得分离与姿控联合仿真的分析结果，若分离仿真结果不满足要求（分离过程中姿态发散程度过大或分离间隙过小等），则返回步骤c对姿态控制律进行优化并重新进行分离/姿控联合仿真分析。

2 火箭分离/姿控一体化仿真平台构建

2.1 分离问题建模

本文研究的火箭头体分离采用气动冷分离方案，上面级为面对称的非传统构型，其在低空大动压环境下具有较好的升阻特性；下面级为近似轴对称构型，通过安装在下面级尾部的液体姿控动力系统在分离过程中对下面级姿态进行控制。分离前体和分离后体的对接面即为头体分离面，分离面处无额外分离能源，仅依靠前后体相对气动力差实现分离。分离前的组合体几何模型如图2所示。

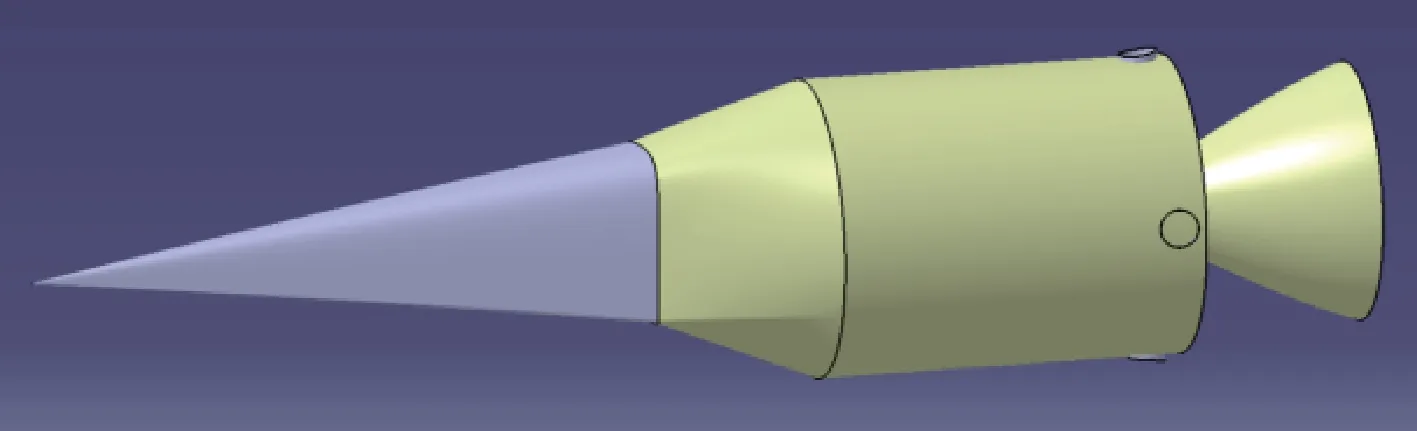
图2 分离前火箭几何模型Fig.2 Geometric model of therocket before separation

分离前体底部存在突出物，伸入分离面173 mm，突出物包络距离分离后体上、下表面碰撞危险点的初始间隙分别为190 mm（上）和200 mm（下）。姿控动力系统位于分离后体尾部，4 个喷管沿周向均匀分布，相邻喷管夹角均为90°。分离过程中无额外分离能源辅助两体分开，当突出物包络完全脱出后体，且未发生碰撞，视为头体安全分离。头体分离位置关系见图3。

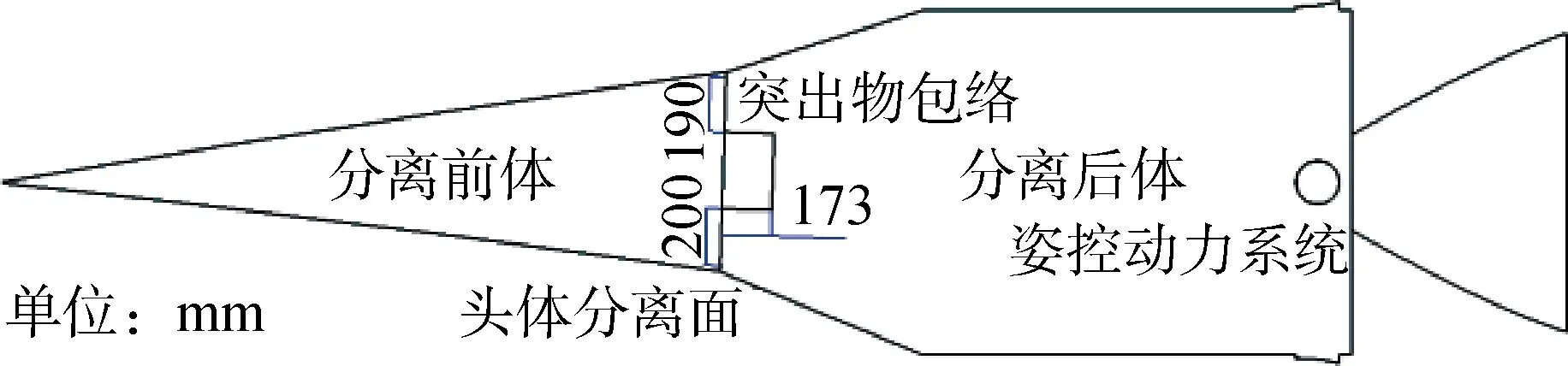
图3 头体分离位置关系Fig.3 Position relationship of head-body separation

分离过程中，姿控动力系统持续工作以调整后体姿态，姿控动力系统喷管位置和性能参数如表1所示。

表1 姿控动力系统性能参数Tab.1 Performance parameters of control power systems

姿控动力系统在工作时会为分离后体同时提供法向/侧向力和转动力矩，从而改变分离后体的运动规律。因此需要开展联合仿真，将姿态控制律与多体动力学方程进行耦合，实现对头体分离运动特性的精确预示。

2.2 分离条件

为使仿真计算模型尽量接近真实状态，火箭姿控动力系统喷管推力模型考虑了10 ms 启动加速性和关机减速性，其余均视为理想状态［7］。分离工况与真实状态保持一致，分离条件：分离攻角为3°，分离动压约为4 000 Pa，姿控动力系统单个喷管推力为1 000 N。

2.3 分离与姿控耦合计算方法

分离后体俯仰通道姿态闭环控制以下面级俯仰角偏差和俯仰角速度偏差为控制输入，姿控动力系统采用基于姿态角和姿态角速度反馈的继电控制率［8］，控制系统结构如图4所示，控制方程见式（5）。

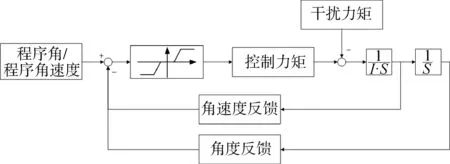
图4 控制系统结构Fig.4 Block diagram of the control system

式中 Δφ为当前姿态角度偏差；Δφc为推力死区对应的角度偏差；为当前姿态角速度偏差；为推力死区对应的角速度偏差；M为控制力矩。将式（5）代入式（1）～（4）能够实现分离动力学与姿态控制联合求解。

2.4 联合仿真平台构建

联合仿真建模和仿真流程见图5。

图5 联合仿真流程Fig.5 Flow chart of co-simulation

通过CAD 软件建立火箭上、下面级参数化的几何模型，对于外形或构成复杂的分离体，可以利用装配完成分离两体建模，然后定义分离体相互约束的运动副，最终生成由几何参数、装配参数、约束参数组成的结构化几何模型。

将结构化几何模型导入多体动力学模块，在分离体几何模型上施加分离相关的作用力及作用力矩，建立分离间隙与碰撞检测模型，生成分离动力学计算模型，并在模块中建立控制系统输入、输出变量，并完成与控制模块的接口定义。

在控制模块中搭建姿控系统模型，完成与多体动力学模块的接口调试和仿真参数设置，如仿真步长、仿真时间、积分算法等，最终完成姿控与分离联合仿真建模。

仿真计算时，多体动力学模块求解动力学与运动学方程，控制模块求解姿态控制方程，并与多体动力学模块完成数据交换，共同完成姿控与分离的联合计算。计算时可通过网络实现多台计算机并行计算，提高仿真效率。

3 分离与姿控联合仿真结果对比

3.1 无控分离情况

基于搭建好的分离/姿控联合仿真框架，对火箭分离过程开展仿真分析。在姿控动力系统不工作的情况下，前/后体仅在气动力作用下实现分离，分离过程如图6～8所示。该工况下前体底部突出物尚未脱出分离面时最小分离间隙已降至0 mm，故分离过程中前体底部突出物会与后体发生干涉碰撞。由图7可以看出，姿控动力系统不工作时后体俯仰角相对前体变化较剧烈，导致分离间隙在较短时间内降至0 mm。

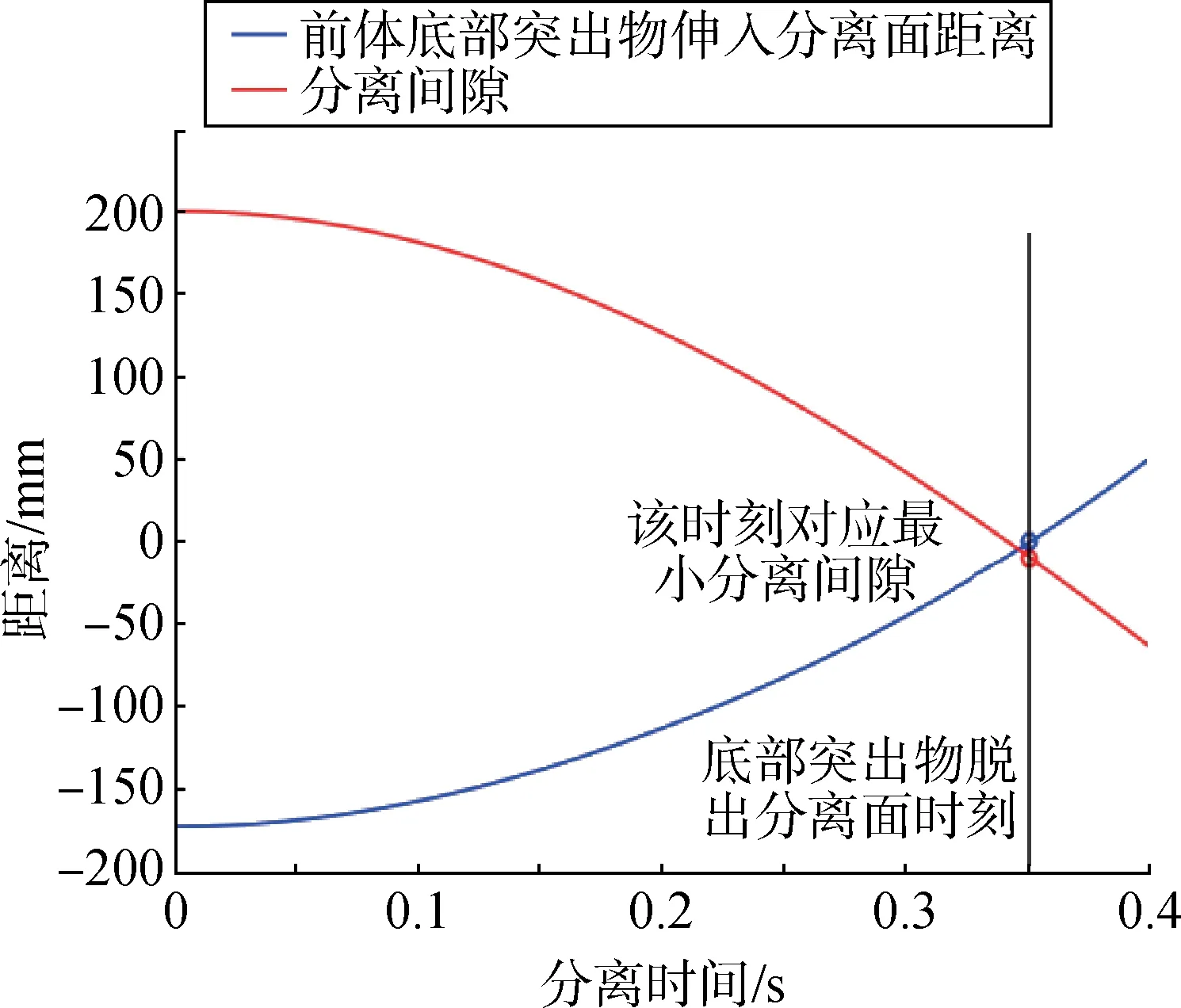
图6 分离间隙（无控）Fig.6 Separation gap (uncontrolled)

3.2 有控分离情况

在姿控动力系统工作的情况下，头体分离过程如图9～11 所示。姿控动力系统工作时分离过程中后体姿态更稳定，前、后体俯仰角差较小。由于姿控喷管推力方向与后体法向气动力方向一致，故由图11 可知，后体相对前体的法向平动速度有所增加，但前体底部突出物脱出分离面时仍有约40 mm 的分离间隙，分离过程中前、后体不发生干涉，能够可靠分离。

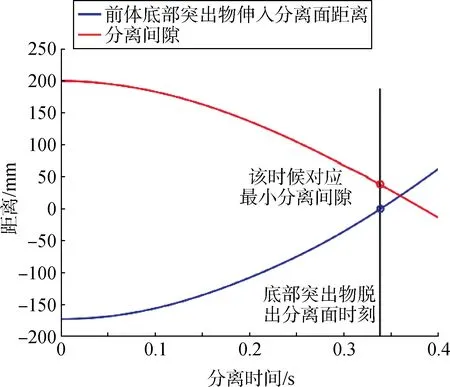
图9 分离间隙（有控）Fig.9 Separation gap (controlled)

分离与姿控一体化设计能够有效解决无控分离过程中前、后体发生干涉碰撞的问题，使火箭能够在不额外增加分离能源的情况下实现前、后体可靠分离。

4 结束语

本文以火箭头体分离问题为研究对象，开展了分离与姿控一体化设计方法研究，结合多种学科分析工具提出了联合仿真流程和建模方法，建立了分离与姿控耦合仿真模型，实现了对有控分离过程的精确仿真预示。基于某火箭分离算例，对无控分离过程和有控分离过程开展了对比分析，结果表明分离与姿控一体化设计能够解决无控分离过程中前、后体发生干涉碰撞的问题，有效增大分离间隙至40 mm以上。分离与姿控一体化设计能够利用箭上现有资源实现可靠分离，有效降低对分离能源的需求，从而起到简化分离装置、减小火箭质量、提升火箭综合性能的作用。