爆轰驱动多介质问题的Lagrange 多分区自适应数值模拟研究1)
周 蕊 李 理 田保林 ,†,
* (北京应用物理与计算数学研究所,北京 100094)
† (北京大学应用物理与技术研究中心,北京 100091)
引言
爆轰波是包含快速化学反应的强间断面.凝聚炸药爆轰过程释放的巨大压力或能量可以使周围介质变形、屈服,甚至产生巨大的损伤效应[1-2].因此,凝聚炸药爆轰在惰性材料约束下的传播发展过程,及其驱动效应一直是工程应用中被广泛研究的关键问题之一[3-5].目前,对于惰性金属材料与凝聚炸药爆轰的相互作用机制认识还存在不足,尤其对于不同约束条件下非理想爆轰过程的规律性认识还有待系统深入地研究[6].
考虑到实验成本和观测手段的局限性,多年来数值模拟一直是研究爆轰驱动多介质问题的重要手段.这一问题是典型的爆轰弹塑性多介质大变形问题,模拟该问题的数值方法大概可以分为两类.一类是欧拉框架下的高精度数值方法[7-12],这类方法的优点是网格固定不动,对大变形问题的适应性强,但存在无法清晰捕捉物质界面,界面附近存在数值耗散等不足.另一类是Lagrange 框架下的数值方法[6,13-14],这类方法因网格跟随流体自适应运动,可以自然地捕捉物质界面或自由面.特别地,Lagrange 框架下适应多分区的考虑接触滑移的交错型数值方法在模拟弹塑性、多介质、薄壳和大空腔等复杂问题时具有独特的优势[15-16],成为工程应用中爆轰驱动多介质问题不可或缺的数值模拟手段[17-19].
为了揭示炸药爆轰和惰性金属介质相互作用时内部的细致流场结构和演化过程,需要在相当密的网格下开展数值模拟研究.然而,Lagrange 方法在较小的网格尺度下对多介质大变形问题进行数值模拟时,存在因网格畸变导致计算不健壮的问题.在上述问题中,我们主要关注的是爆轰反应区附近及金属材料中冲击波附近区域的流场结构和相互作用规律,为了避免整体密网格Lagrange 计算带来的效率和健壮性困难,发展适应凝聚炸药爆轰驱动多介质问题的Lagrange 网格自适应方法(adaptive mesh refinement,AMR)是十分必要的.这可以在保障我们关心区域网格分辨率的同时,粗化爆轰波或激波后膨胀区的网格尺度,提升波后大变形区域Lagrange计算的健壮性.
已有AMR 方法多是基于欧拉框架[20],采用分层的结构网格块自适应加密所关心的流场区域.在欧拉框架下因网格固定不动,不同层网格分别计算后,一般通过时间自适应处理不同层网格边界之间的衔接,这方面已发展了相对成熟的数值算法.在Lagrange 框架下的AMR 方法研究并不多见,Anderson等[21]曾将欧拉框架下结构网格AMR 方法拓展到Lagrange 框架下,发展了相适应的层间耦合算法.Wang[22]发展了适应复杂材料响应过程的ALE-AMR方法.王瑞利等[23]基于多介质流体力学程序LAD2D发展了非结构网格Lagrange 自适应方法.然而,以上工作都未见在复杂几何边界、多分区和多介质问题上的应用.Morrell 等[24-25]基于CORVUS 程序发展了基于cell 的非结构网格自适应方法,实现了跨不同物质区的自适应模拟.然而,他们采用基于“连通数组”的数据结构,这类数据结构与程序紧耦合,不易推广,且随着加密层数的增多,程序实现的复杂程度越来越大.
本文针对凝聚炸药爆轰驱动多介质问题精密化模拟需求,提出了一种新的Lagrange 非结构网格多层自适应方法,及其与接触滑移的自适应耦合算法,实现了弹塑性、多介质和多分区问题的Lagrange 自适应数值模拟能力.该方法既发挥了非结构网格分层数据结构的灵活性优势,也通过将有效网格压至一层进行Lagrange 计算,避免了传统AMR 中不同层级网格分别计算带来的层间耦合困难.采用该方法开展了拐角爆轰、多层炸药隔爆和有限尺寸弯道爆轰等复杂问题的数值模拟研究.计算结果显示,在保障爆轰波、激波附近网格分辨率的前提下,该模拟方法可大幅缩减可计算网格规模,提升Lagrange计算的健壮性,获得了丰富的凝聚炸药爆轰与惰性金属材料相互作用的流场信息,可为揭示其中的相互作用规律提供丰富的定量数据.
1 适应多分区的Lagrange 非结构网格多层自适应方法
本文基于二维爆轰弹塑性流体力学Lagrange 程序发展非结构网格多层自适应方法,基础算法的具体细节可参考文献[13,26].该程序的主要控制方程是考虑弹塑性[27]和复杂状态方程的流体力学守恒方程组,具体形式如下
其中 β=1 为平面问题,β=0 为以z方向为对称轴的轴对称问题.ρ 和e分别代表密度和比内能.vr和vz分别是r方向和z方向的速度.σrr,σzz,σθθ和σrz是Cauchy 应力张量.τ 是偏应力张量,应力与偏应力满足如下关系
式中 τ 由以下本够方程求得,压力p由状态方程求得.
为了使方程系统封闭,需要引入不同材料的状态方程,本文凝聚炸药采用JWL 状态方程[28].其中未反应炸药的状态方程形式如下
炸药爆轰反应产物的状态方程形式如下

表1 炸药状态方程参数取值Table 1 The equation of state parameters for high-explosive
凝聚炸药爆轰反应过程用Lee-Tarver 三项式反应率模型,具体形式如下
其中 λ 为炸药的反应份额,λ=0 时代表未反应炸药,λ=1时代表爆轰产物.式中的I,b,a,x,G1,c,d,y,G2,e,g,z为反应率模型参数.本文计算所用的炸药反应率模型参数取值如表2 所示.

表2 炸药Lee-Tarver 三项式反应率模型参数取值Table 2 The Lee-Tarver parameters for high-explosive
其中e为比内能,a0,s,Γ0为状态方程参数.本文数值算例涉及的金属材料包括钢和铝,它们的状态方程参数取值如表3 所示.
表3 金属材料 M ie-Grneisen 状态方程参数取值Table 3 The M ie-Grneisen equation of state for steel and aluminium
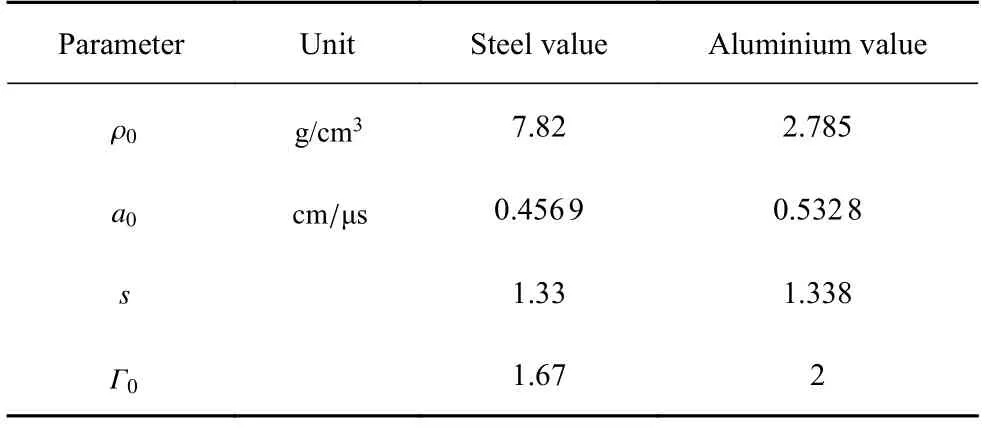
表3 金属材料 M ie-Grneisen 状态方程参数取值Table 3 The M ie-Grneisen equation of state for steel and aluminium
上述控制方程的离散基于交错型Lagrange 格式,详细的离散过程可参考文献[26],篇幅原因,本文不再赘述.所有的热力学量定义在单元中心上,例如 ρ,τ,p,e等;速度v定义在网格节点上.在Lagrange计算中,每一个单元的质量是守恒的,单元密度由初始质量除以当前体积求得.动量方程采用基于面格式的有限元方法离散,内能方程基于有限体积格式离散.在上述方法体系下,需要引入人为黏性捕捉激波间断,使得人为黏性耗散产生的熵增等于激波引起的物理熵增,以此来达到正确模拟激波波前和波后状态关系的目的.本文采用文献[26]中人为黏性形式,具体形式如下
其中,二维问题中l=为网格的特征尺度,A为网格面积,为应变率张量,a为声速.C0和C1为无量纲参数,在本文的算例中取值分别为1.5 和0.06.
为了适应多分区多介质问题,采用接触滑移算法处理不同物质之间的相互作用.本文采用基于分配参数思想的接触滑移算法[29-30],它可以处理接触后两接触面具有相对切向滑移、由分开到接触、由接触到分开等复杂情况的问题.这类方法在我们关心的多介质大变形相关工程问题中被广泛应用.
自适应数据结构的构建和层间耦合策略是自适应方法的核心.此外,考虑到我们关心的问题是多介质、多分区的,网格自适应与接触滑移的耦合算法也是本研究需要解决的关键问题之一.下边将分别介绍这些内容.
1.1 非结构数据结构及加密准则
非结构多层数据结构是实现Lagrange 多层AMR 的重要基础.在这个数据结构中,我们设计了“单元类”、“边类”、“节点类”等自定义数据类型.
(1) “单元类”中提供单元相关的几何信息、物理量信息、自适应信息,如表4 所示.具体如下.

表4 “单元类”中定义的变量及其物理含义Table 4 The variables and their meanings in “cell type”
①单元几何信息:单元在当前网格层上的非结构标识号cell_ID;组成单元的节点在当前网格层上的标识号cell_point(1:N_Point),其中N_point 为组成单元的节点数,本文取值为4;组成单元的边在当前网格层上的标识号cell_edge(1:N_edge),其中N_edge 为组成单元的边数,本文取值为4;共边单元在当前网格层上的标识号sameedge_cell(1:N_edge).
②单元物理量信息:材料标识mat;自适应加密准则用到的单元量,例如压力pressure、密度density、压力梯度P_grad、密度梯度ρ_grad、爆轰反应份额fac 等.
③单元自适应信息:在当前网格层上单元即将被加密的层数level;父单元在其所属网格层上的局部单元标识号father_cell;子单元在下一网格层上的局部单元标识号son_cell(1:4),如果当前网格层上单元被加密,那么相应单元将一分为4,形成4 个小单元加入到下一网格层中.
(2) “边类”中提供与边相关的几何信息和自适应信息,如表5 所示.具体如下.
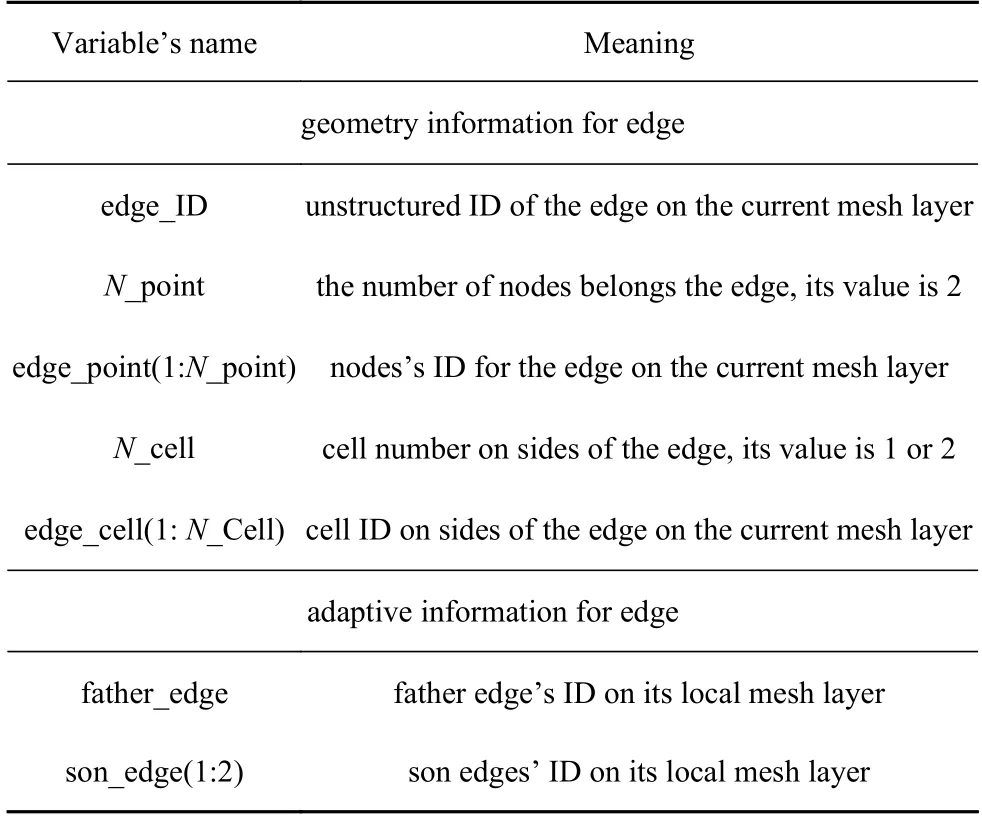
表5 “边类”中定义的变量及其物理含义Table 5 The variables and their meanings in “edge type”
①边几何信息:边在当前网格层上的非结构标识号edge_ID;组成边的节点在当前网格层上的标识号edge_point(1:N_point),其中N_point 为组成边的节点数,本文取值为2;边两侧单元在当前网格层上的标识号edge_cell(1:N_cell),其中N_cell 为边两侧的单元数,如果边是计算的边界,那么N_cell 取值为1,否则取值为2.
②边自适应信息:父边在其所属网格层上的局部标识号father_edge;如果边所在的单元被加密,子边在下一层网格上的局部标识号son_edge(1:2).
(3) “节点类”中提供与网格节点相关的几何信息、物理量信息和自适应信息,如表6 所示.具体如下.

表6 “节点类”中定义的变量及其物理含义Table 6 The variables and their meanings in “node type”
①节点几何信息:节点在当前网格层上的非结构标识号node_ID;节点周围的单元在当前网格层上的标识号node_cell(1:N_cell),其中N_cell 为节点周围的单元数量,取值在1~4 之间;节点相连的边在当前网格层上的标识号node_edge(1:N_edge),其中N_edge 为与节点相连的边的个数,取值为2 或4.
②节点物理量信息:节点位置node_r,node_z;节点边界条件标识node_boundarycondition,存在3 种类型,0 代表自由边界,1 代表r方向约束,2 代表z方向约束,3 代表固定不动,4 代表滑移边界.
③节点自适应信息:对应上一网格层上的节点局部标识号father_node;对应下一网格层上的节点局部标识号son_node.如果当前层节点在上一层或下一层网格上没有对应的节点,那么对应节点标识号为0.
以上数据结构是普适且独立的,它不依赖于程序底层和数值算法.根据物理需求,我们首先确定基础层网格,它可以是整个计算域的网格,也可以是其中的一部分.将基础层网格信息装配到上述非结构数据结构中,根据物理过程特点,确定每个基础层单元的加密层数.对于凝聚炸药区,我们一般采用反应份额作为网格加密判据;对于金属材料区,我们采用密度梯度或压力梯度作为网格加密判据.首先,我们设置最高加密层数为L,通过加密判据先确定基础层网格上加密层数为L的单元.举例来说,对于炸药区,我们将反应份额大于0.01,小于0.99 的单元加密层级标识为L.随后,通过非结构数据结构中的“单元类”中的共边单元信息,确定加密L-1 层的单元.以此类推,直到加密层级为1 的单元确定完成为止.因此,所有基础层网格上的单元加密与否,以及加密层数被确定.在上述加密策略中,相邻基础层单元的加密层级最多相差一层,这个约束条件对于后文中的层间耦合是非常重要的.
为了便于理解,我们给出一个简单的示例来更清楚地解释基础层网格单元加密层级确定的过程.如图1 所示,在一个方形平面计算域中,初始时刻在原点附近给定一个高压,形成散心爆轰波向外传播.在某时刻,基础层网格上的反应份额分布如图1 所示,我们将反应份额在0.01~0.99 之间的单元加密层级确定为3 层,由此确定了如图2 左图所示的红色单元的加密层级为3.根据基础层网格上红色单元的共边单元信息,确定了如图2 中间图所示的绿色单元加密层级为2.进一步地,由绿色单元的共边单元信息,确定了如图2 右图所示的蓝色单元加密层级为1.至此,确定了基础层网格上所有单元的加密层级.
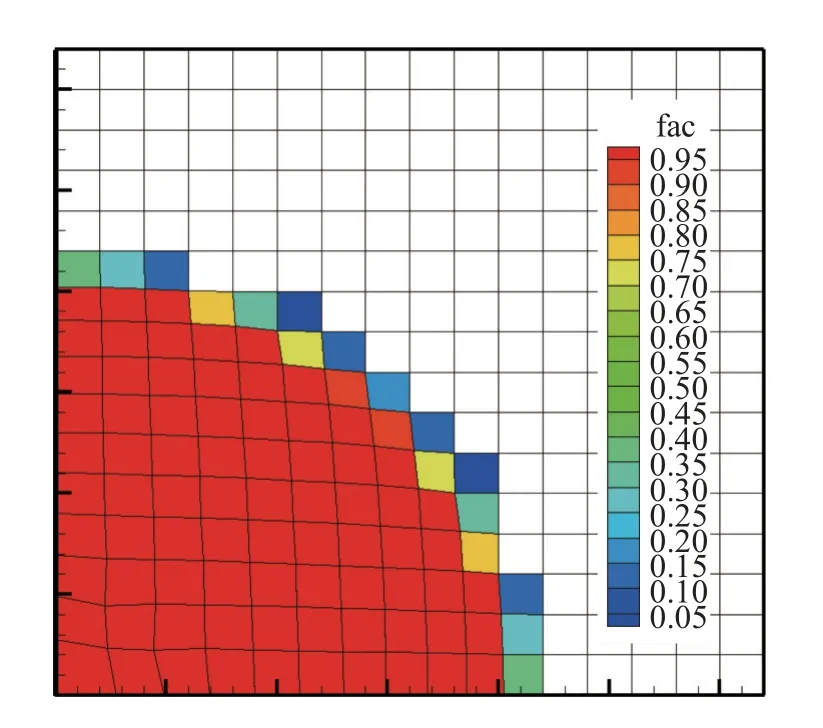
图1 基础层网格及爆轰反应份额分布(仅显示了反应份额大于0.01 的单元)Fig.1 Basic coarse mesh and its reactive variable distribution

图2 基础层网格上单元加密层级Fig.2 Refinement levels of the basic coarse cells
在非结构多层数据结构中,第0 层网格信息与基础层网格信息一致.按照前述过程确定了第0 层网格上每个单元的加密层级.如图3 网格细分过程示意图所示,假设第0 层网格上的4 个单元C0_1,C0_2,C0_3,C0_4 加密层级分别为3,1,2,0.对于单元C0_4 不存在子单元,不会出现在下一层网格信息中.第一层网格数据信息的构建以第0 层数据信息为基础,在第0 层网格上,如果单元在当前网格层上的加密层级不小于1,那么这个单元被细分为4 个小单元,这4 个小单元加入到第1 层网格数据信息中.在第1 层网格上,所有被0 层网格细分后的小单元都有一个局部标识号,如图3 中第一层网格上单元C1_1,···,C1_12.这12 个单元在当前网格层上的加密层级等于父单元的加密层级减1,即C1_1,···,C1_4 这4 个单元在第一层网格上的局部加密层级为2,C1_5,···,C1_8 这4 个单元在第一层网格上的局部加密层级为0,C1_9,···,C1_12 这4 个单元在第一层网格上的局部加密层级为1.按照这个思路,就完成了第一层网格非结构数据信息的构建.同样地,基于第1 层网格的非结构数据信息,如果单元当前加密层级不小于1,那么这个单元被细分为4 个小单元,这4 个小单元加入到第2 层数据信息中,如图3中第2 层网格上的单元C2_1,···,C2_32.这32 个单元在当前网格层上的加密层级等于父单元的加密层级减1,即C2_1,···,C2_16 这16 个单元在第2 层网格上的局部加密层级为1,C2_16,···,C2_32 这16 个单元在第二层网格上的局部加密层级为0.这样就构建了第二层网格上的非结构数据信息.以此类推,基于第2 层网格的非结构数据信息,如果单元当前加密层级不小于1,那么这个单元被细分为4 个小单元,这4 个小单元加入到第3 层数据信息中.如图3中第3 层网格上的单元C3_1,···,C3_64.
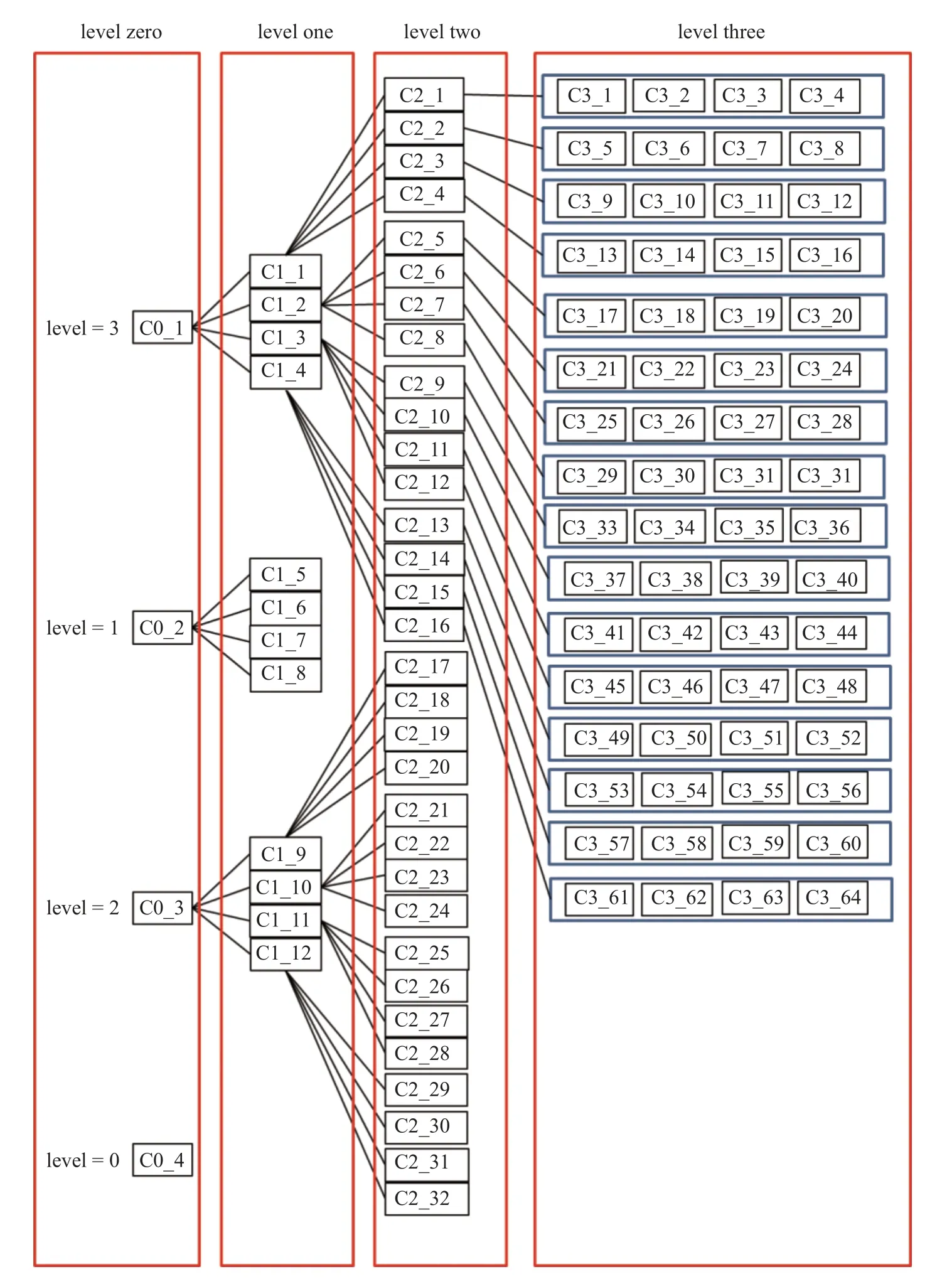
图3 网格细分过程示意图Fig.3 Schematic diagram of mesh subdivision progress
按照上述网格细分过程,在每一层网格上都形成了当前层的“单元类”、“边类”、“节点类”信息,因此,当前层上局部单元-边(cell_edge)、单元-节点(cell_point)、共边单元(sameedge_cell);边-单元(edge_cell)、边-节点(edge_point);节点-单元(node_cell)、节点-边(node_edge)等几何信息被构建.此外,相邻网格层之间的连通信息也被构建,例如单元-子单元(son_cell(1:4))、单元-父单元(father_cell)、边-子边(son_edge(1:2))、边-父边(father_edge)、点-上一层节点(father_node)、点-下一层节点(son_node)等.图1 所示算例按照上述过程,形成了非结构分层网格信息如图4 所示.

图4 非结构分层网格信息Fig.4 Unstructured hierarchical mesh information
1.2 层间耦合方法
在传统的AMR 方法中,在每一层网格上分别进行求解,通过相邻层之间的边界条件处理不同层级网格之间的耦合.这类方法在网格固定不动的欧拉框架下是相对成熟和完善的[20].在Lagrange 框架下,网格跟随流体运动,不同层级网格如果分别进行计算,在层间边界上会涉及复杂的时间和空间双重自适应,实现起来是相当困难的.本文通过提取不同层级网格之间的连通信息,实现不同层级上有效网格压至一层进行Lagrange 计算的AMR 策略,避免了Lagrange 分层计算层间耦合的困难.
具体来说,在第0 层网格上(图3 第1 列),如果单元的当前加密层级为0,那么该单元加入到有效计算单元队列中,即C0_4 单元加入到有效计算网格中.在第1 层网格上(图3 第2 列),如果单元在当前层上的局部加密层级为0,那么该单元被加入到有效计算单元队列中,即C1_5,···,C1_8 单元加入到有效计算网格中.以此类推,图3 中第3 列的C2_17,···,C2_32 单元,以及第4 列中的C3_1,···,C3_64 单元加入到有效计算网格中.可见,加入拟计算非结构网格中的有效单元都没有子单元,在当前层有子单元的网格会被下一层子单元所覆盖.按照上述思路,图4所示的多层网格中,有效计算网格如图5(a)所示,不同颜色代表不同层网格提取的有效网格单元,最终用于Lagrange 计算的整体最密非结构网格构建完成,如图5(b)所示.通过上述过程,实现了多层非结构网格分层存储,有效网格压至一层进行Lagrange计算的AMR 策略.

图5 不同层级上有效网格被压至一层,形成Lagrange 计算的整体非结构网格Fig.5 Multi-level meshes are flattened onto the final global unstructured mesh
当不同层级网格被压至一层时,悬点会出现在层间边界上.在相邻单元加密层最多相差一层的约束下,网格边上最多只有1 个悬点,如图6 所示.本文借鉴文献[25]中的方法对悬点施加约束.假设悬点为无质量和动量的虚拟点,小单元计算得到的悬点上的节点质量和节点动量按比例分配给相连非悬点节点,悬点的速度和Lagrange 运动位置由相连非悬点节点的速度和位置插值得到.
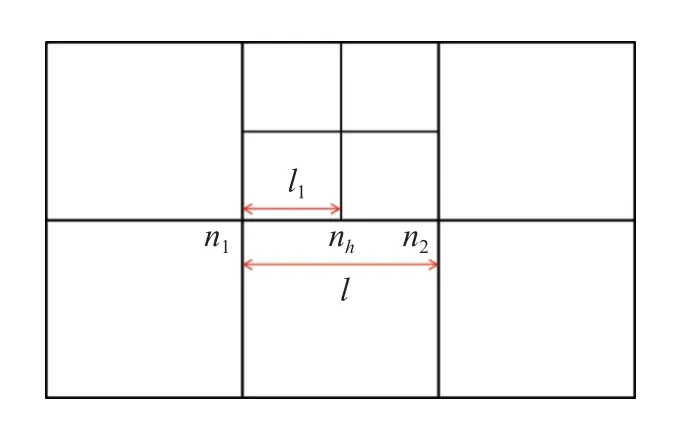
图6 悬点周围网格分布示意图Fig.6 Schematic diagram of mesh distribution around the hang point
具体来说,在图6 中,节点nh为悬点,节点n1和n2为与nh相连的两个规则节点.l1为节点n1与节点nh的距离,l为两个规则节点n1与n2之间的距离.定义比例因子f由下式计算
那么,悬点nh的速度和坐标位置由规则节点n1和n2的速度和坐标位置计算得到,具体形式如下
两个规则节点的质量和节点力按如下公式进行修正
以上悬点计算方法在文献[24-25]中被成功应用,该约束方法解决了层间耦合的问题.然而,对于悬点计算方法的深入系统分析还有待后续进一步开展.
1.3 自适应接触滑移耦合方法
本文采用的接触滑移算法需要人为事先给定主线和从线,由此得到对应的主点、主单元、从点和从单元.具体计算流程包括:判断主从点接触状态、对符合条件的主点施加接触约束、计算相互作用后主点的加速度、计算产生碰撞后的主点速度、计算从点的速度和加速度、调整下一步时间步长.在Lagrange 自适应计算的过程中,如果主单元或从单元被自适应加密或粗化,那么滑移线的几何拓扑势必会发生改变.本文提出了接触滑移与Lagrange 自适应算法的“紧耦合”策略.具体来说,在1.1 节中构建的分层非结构数据结构中,在每一层网格上增加滑移线的几何信息,通过已经构建的不同层级网格之间的连通信息,即能提取出滑移线的单元、节点在相邻层级上的连通信息.通过提取这些连通信息,可以在形成整体Lagrange 计算非结构密网格的同时,自适应形成新的滑移线几何拓扑.
图7 给出了一个示例,计算域中包含两块炸药区,初始时刻在原点附近给定一个高压,散心爆轰波逐渐向外传播,从下边的炸药区传至上边的炸药区.上边的炸药区定义为滑移线的主侧,下边定义为从侧.计算到某一时刻,自适应网格分布如图7(a)所示,图中蓝色线为滑移线所在位置.我们将红色矩形围起的区域放大,如图7(b)和图7(c)所示.在基础层网格上,从单元的全局单元编号依次为211,212,213,···,对应主单元的全局单元编号为191,192,193,···,如图7(b)所示.通过提取和搜索相邻网格层上的滑移线几何连通信息,形成新的整体非结构密网格上的滑移线几何拓扑关系.如图7(c)所示,新的从单元全局编号依次为184,328,331,540,543,552,555,···,对应的主单元的全局编号为173,325,326,529,530,533,534.
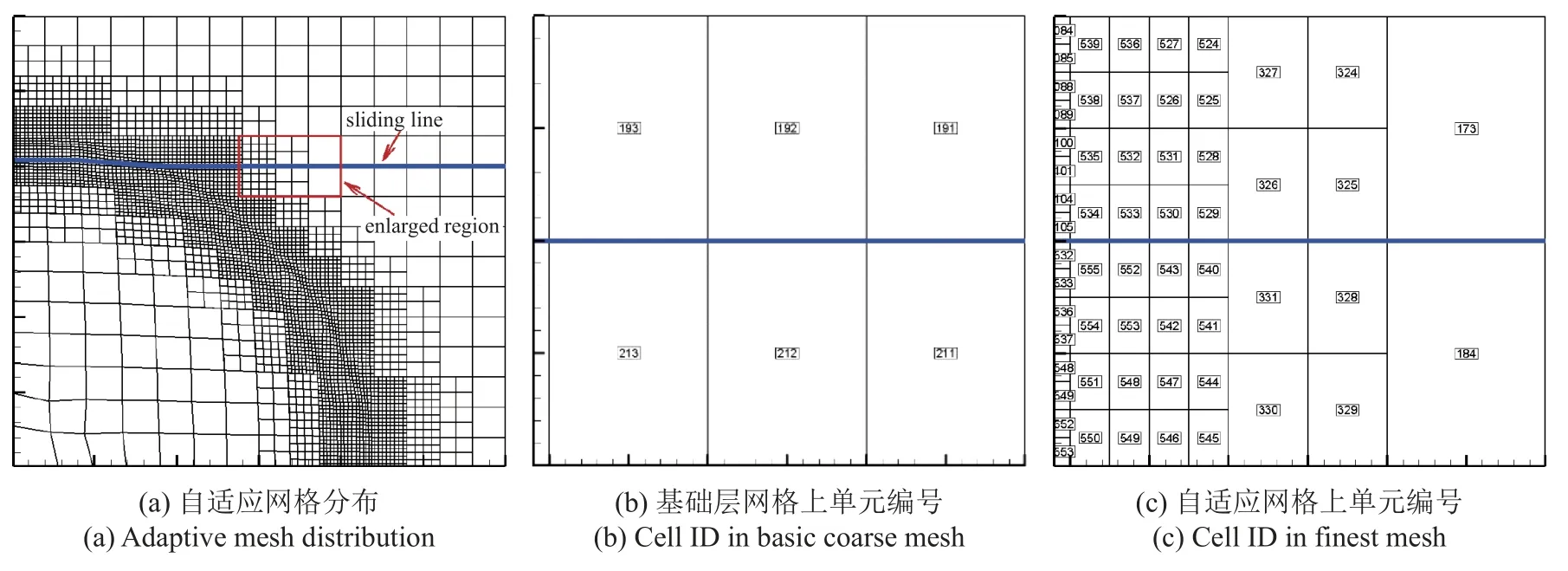
图7 接触滑移算法与Lagrange AMR 方法耦合,形成新的接触滑移几何拓扑Fig.7 New geometric topology of the sliding interface is rebuilt in the adaptive coupling strategy
1.4 Lagrange 自适应计算流程
完成上述AMR 方法设计的基础上,按照如图8所示的流程实现上述AMR 策略与Lagrange 主体算法的耦合.首先,提取用于自适应计算的基础层网格,将其装配至非结构自适应数据结构中.然后,根据所关心物理问题的特点确定自适应加密准则,基于此,确定基础层网格上每个单元的加密层级.随后,分层构建非结构网格数据信息,得到每一层网格上所有的几何信息、自适应连通信息以及必要的物理量信息.最后,提取出用于Lagrange 计算的有效非结构网格信息,以及悬点和滑移线信息,将它们传回给Lagrange 主体算法开展Lagrange 计算.在Lagrange计算的过程中,需要实时监测自适应网格分布是否满足物理过程特点,根据监测判据开展新的自适应信息的构建.
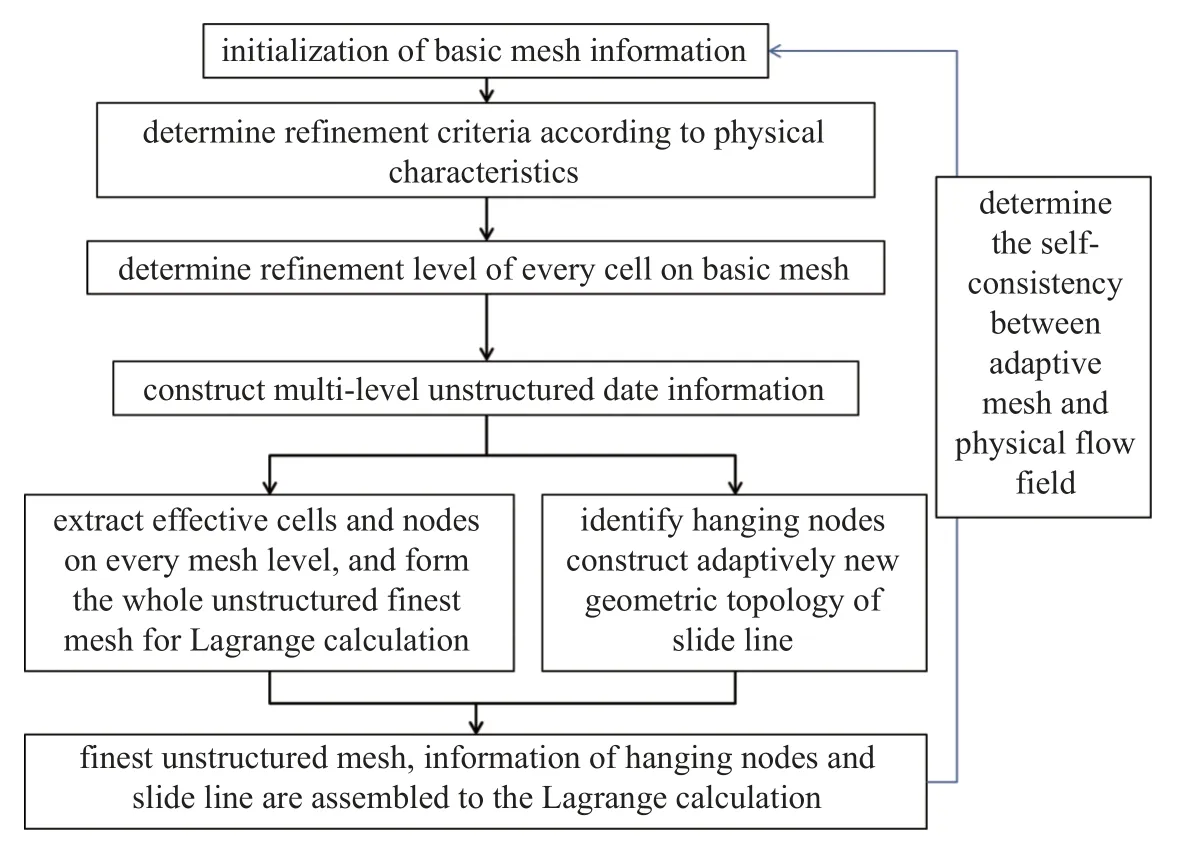
图8 AMR 与Lagrange 主体算法耦合流程Fig.8 Coupling low between the AMR and Lagrange algorithm
以前文中提到的简单算例为例,给出自适应网格更新的步骤如下.
(1) 假设自适应计算至某一时间步,Lagrange 计算网格分布如图9(a)所示,自适应非结构数据结构中存储了完备的用于计算的非结构网格几何信息和物理量信息.基于这个密网格,得到对应基础层网格上的必要物理量.基础层网格的节点位置由自适应网格上对应节点位置直接赋值得到,物理量由相交重映计算得出.需要强调的是,这个过程中只重映与加密判据相关的物理量即可.例如,对于爆轰问题来说,只重映反应份额即可.基础层网格上的反应份额分布如图9(b)所示.

图9 自适应网格更新流程Fig.9 Update process of adaptive mesh
(2) 根据图2 所示流程,确定基础层网格上每个单元是否加密,以及加密层级,如图9(c)所示.图中红色单元加密层级为3,绿色单元加密层级为2,蓝色单元加密层级为1.
(3) 按照图3 所示流程,分层构建非结构数据信息,如图9(d)所示.由此得到每一网格层上局部几何拓扑关系,以及相邻层级之间的自适应连通信息.
(4) 通过提取不同层级之间的连通信息,获得有效计算非结构密网格的数据信息,新的压至一层的自适应非结构网格分布如图9(e)所示.
(5) 通过以上步骤,得到旧自适应网格(图9(a))的几何信息和物理量信息,以及新自适应网格(图9(e))的几何信息.采用非结构相交重映方法获得新自适应网格上的物理量信息.
(6) 图9(e)所示的自适应网格几何信息和物理量信息传回给主体程序进行后续的Lagrange 计算.随后,根据加密判据,返回步骤(1).
2 算例验证
考虑到采用的爆轰弹塑性流体力学Lagrange程序已经经过多种复杂算例的验证与确认,对凝聚炸药爆轰过程的模拟有较高的置信度.例如对于典型PBX9404 炸药的一维爆轰传播过程,数值计算得到的稳定爆轰波传播速度为 0.8817 cm/μs,相同条件下,根据Rayleigh-Hugoniot 关系推导的理论爆轰波传播速度为 0.8808 cm/μs,可见数值模拟结果与理论解的偏差仅为0.1%.因此,在本节的数值验证中,一般将一致均匀密网格的数值模拟结果作为基准解,将Lagrange 自适应模拟结果与其定量比较,来说明所提出自适应方法模拟结果的正确性.
我们采用一维爆轰传播问题考核所提出Lagrange非结构网格多层自适应方法的正确性.图10 为一维爆轰传播问题的数值模拟结果.初始时刻,在炸药左端设置高压区起爆爆轰波,在爆轰波传播的过程中,自适应密网格一直跟随爆轰波阵面移动,使得爆轰反应区附近一直保持预设的网格分辨率.将自适应加密3 层的模拟结果与同程度均匀密网格模拟结果进行定量比较,如图10 所示,相同时刻爆轰反应区附近的网格分布及压力分布完全一致.两种方式计算得到的最大压力均为36.98 GPa,爆轰波位置均在z=12.5567 cm 处,验证了Lagrange 自适应模拟方法的正确性.自适应模拟在保证爆轰反应区网格分辨率的前提下,相比于均匀一致加密,节省95%的网格规模.
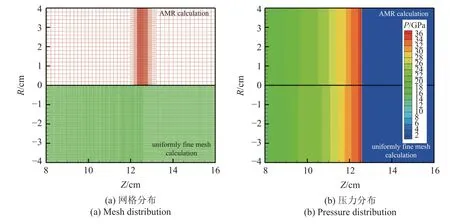
图10 一维爆轰传播问题 (上:AMR(加密3 层)计算结果,下:一致密网格计算结果)Fig.10 1D detonation propagation (up:AMR calculation,down:uniformly fine mesh calculation)
为了定量考核Lagrange 多层自适应方法与接触滑移耦合算法的正确性,我们设计了如图11 所示的一维爆轰传播算例.这个算例包括3 个物质区.2 条滑移线、2 种材料,同时还存在滑移线相交的情况.该问题本质上是一维问题,初始时刻,在左侧金属材料钢区与右侧两块炸药之间存在空隙,需采用开穴滑移算法计算.两块炸药之间的滑移线不考虑相对滑动,采用束缚滑移算法计算.初始时刻,在炸药区左侧设置高压区起爆爆轰波,爆轰产物膨胀会使金属与炸药之间的空隙闭合.如图11 所示,Lagrange自适应方法能正确模拟含复杂滑移线(含相交)情况的算例.图11(b)和图11(c)分别为采用自适应方法模拟和同程度均匀密网格模拟的压力分布,两种方式模拟在相同时刻的爆轰波位置和爆轰波附近压力分布定量一致,最大压力均为36.9548 GPa,爆轰波面位置在z=3.8349 cm 处,验证了Lagrange 自适应方法与接触滑移耦合算法的正确性.

图11 含多条滑移线的一维爆轰传播问题,蓝色实线为滑移线所在位置Fig.11 1D detonation propagation with slide line,blue solid line is slide line
更进一步地,我们设计了如图12 所示的二维爆轰传播与对碰问题,来考察Lagrange 多层自适应方法对于多点起爆、爆轰波对碰等复杂波系结构的适应性.我们分别在两个角点处设置局部高压起爆爆轰波,两道爆轰波相向传播直至对碰.如图13 和图14 所示,在爆轰波传播与对碰的过程中,自适应密网格有效地跟随激波运动.随着两道爆轰波靠近、对碰,两块非结构自适应密网格自动衔接.同时,在相同时刻自适应加密3 层的模拟结果与同程序均匀一致密网格模拟的爆轰波阵面位置和波系结构一致,体现了所发展Lagrange 多层自适应方法对复杂问题的适应性.
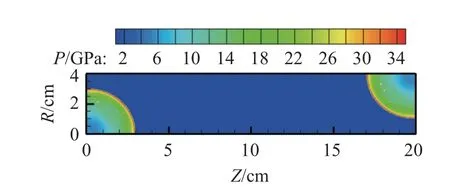
图12 二维爆轰传播与对碰问题、压力分布 (t=3 μs)Fig.12 2D detonation propagation and collision,pressure distribution (t=3 μs)
3 爆轰驱动多介质问题的Lagrange 自适应模拟
本节开展拐角爆轰、多层炸药隔爆、有限尺寸弯道爆轰等复杂爆轰驱动多介质问题的Lagrange自适应数值模拟研究.
3.1 拐角爆轰问题
本文所模拟的拐角爆轰问题,初始计算域为(0.0,20.0 cm)×(0.0,10.0 cm),其中金属材料钢的初始几何尺寸为(0.0,8.0 cm)×(0.0,6.0 cm),剩下的区域为凝聚炸药.基础层网格划分100×50 个单元,对应网格尺寸为0.2 cm.在这个轴对称问题中,初始时刻在炸药区左侧设置高压区域,形成爆轰波遇金属材料拐角形成复杂的爆轰波绕爆过程.在炸药中,采用反应份额作为加密判据,当单元反应份额介于0.01~0.99 之间时,单元加密3 层.在金属材料中,采用密度梯度作为加密判据,当密度梯度大于0.05 时,相应单元加密3 层.自适应加密后,最小网格尺寸为0.25 mm.如图15 和图16 所示,自适应计算的密网格始终跟随爆轰波阵面及金属中冲击波移动,有效模拟了爆轰波沿金属边界传播,及遇金属拐角绕爆的过程.一致密网格模拟得到的爆轰波传播和绕爆过程与自适应模拟结果一致.自适应计算拐角处节点起跳时间为8.8143 μs,一致密网格计算拐角处节点起跳时间为8.8066 μs,相差小于0.1%.自适应计算中爆轰波附近加密3 层实际计算网格总数不超过3 万,而同程度一致密网格计算网格总数为32 万.

图16 轴对称多介质拐角爆轰问题模拟结果 (t=10 μs)Fig.16 Axisymmetric multi-material corner detonation problem (t=10 μs)
3.2 多层炸药隔爆问题
在实际工程中,除了经常出现爆轰绕爆这一复杂现象,爆轰波过金属隔爆也是常见现象.为此,设计了如图17 所示的多分区、多介质问题,这个算例包含4 个物质区、3 条滑移线、3 种材料,存在爆轰波传播、过金属隔爆等复杂物理过程.炸药与金属之间允许切向移动,接触滑移计算采用单纯滑移算法.两块炸药的初始位置分别为(0.0,20.0 cm)×(0.0,2.0 cm) 和 (0.0,20.0 cm)×(2.4 cm,4.4 cm);两块炸药之间的金属为铝,其初始几何位置为(0.0,20.0 cm)×(2.0 cm,2.4 cm);炸药外边界处的金属为钢,其初始几何位置为(0.0,20.0 cm)×(4.4 cm,4.8 cm).初始时刻,在坐标原点附近设置高压点起爆爆轰波,爆轰波在下方第一块炸药中形成散心爆轰向外传播,驱动中间层金属材料,压缩引爆上方第2 块炸药,产生隔爆.随后在两块炸药中形成两个爆轰波同步向右侧传播.如图17 和图18 所示,我们仅在炸药区采用反应份额作为自适应加密判据,将爆轰波阵面附近网格自适应加密3 层.在整个爆轰传播发展的过程中,自适应密网格都能有效地捕捉爆轰波所在位置,实现爆轰波阵面附近的高分辨率模拟.自适应加密3 层与同程度均匀密网格模拟的爆轰波阵面附近压力分布是一致的,验证了该Lagrange 多层自适应方法对复杂问题的适应性.在这个问题中,自适应模拟最大网格规模为1.3 万,同程度均匀密网格模拟网格规模为12.84 万,可见自适应模拟节省了90%以上的计算量.

图17 多分区炸药爆轰隔爆问题模拟结果 (t=4 μs)Fig.17 Multi-block multi-material detonation problem (t=4 μs)

图18 多分区炸药爆轰隔爆问题模拟结果 (t=10 μs)Fig.18 Multi-block multi-material detonation problem (t=10 μs)
3.3 有限尺寸弯道爆轰问题
有限尺寸弯道中的爆轰问题广泛存在于军用装备起爆系统的设计中,因炸药截面尺寸较小,一般在毫米量级,若采用欧拉高精度方法,在弯道与炸药之间的界面处会存在明显的数值耗散,使得无法准确获得爆轰亏损效应等定量结果.针对有限尺寸弯道爆轰问题,我们提出的基于爆轰弹塑性多介质流体力学程序的Lagrange 非结构网格多层自适应方法会比较适用.我们设计了如图19 所示的算例,直管段长度为1 cm,弯道炸药内半径为1 cm,炸药截面厚度为0.2 cm,弯道炸药内、外各放置一层金属钢,厚度均为0.2 cm.爆轰波在直管端部起爆后,形成一维爆轰进入弯道沟槽中,因金属材料边界曲率的影响,凝聚炸药爆轰与惰性金属材料之间存在复杂的相互作用.初始时刻沿圆周方向炸药区设置210 个网格,半径方向设置10 个网格,内侧钢和外侧钢网格规模与炸药区一致.初始径向网格尺寸为0.2 mm,计算中设置自适应加密层数为3,因此最小网格尺寸为0.025 mm.在炸药区,自适应加密判据为0.01<λ<0.99,其中 λ 为反应份额;在金属材料钢中,自适应加密判据为 ∇p>3.5,p为网格单元的压力.采用接触滑移算法处理炸药与金属钢之间的相互作用,在这个算例中,采用切向不做约束的单纯滑移算法,实际计算中炸药与钢之间会存在摩擦,这方面的影响在日后的研究中会深入开展.

图19 有限尺寸弯道爆轰问题初始几何 (绿色:高能炸药,蓝色:金属钢,红色:CJ 状态爆轰产物)Fig.19 Initial geometry of detonation problem in finite-size curved pipeline (green:high-explosive,blue:steel,red:reactive product of CJ state)
图20 给出了弯道爆轰不同时刻的流场分布.如图20(a)所示,在直管中,形成稳态爆轰波自下而上传播,流场和自适应加密网格沿直管中线左右对称.需要注意的是,因侧向约束的影响,爆轰波阵面在炸药与金属交界处略有弯曲,这个侧向影响会使爆轰波传播能量产生一定亏损.随后,直管中爆轰波传入弯道中,如图20(b)~图20(d)所示,靠近内界面的爆轰波被稀疏,靠近外界面的爆轰波被压缩,出现了复杂的非理想爆轰现象.爆轰波在弯道中传播的过程中,密网格始终跟随爆轰波阵面和金属钢中激波自适应加密,波后膨胀区网格自适应稀疏.在这个复杂几何构型中,Lagrange 自适应模拟即能清晰地保持物质界面,保障激波间断处网格分辨率的同时,缓解均匀密网格计算该问题时波后流场因网格大变形、畸变导致的计算不健壮的问题.在这个问题中,自适应模拟最大网格规模约4 万,同程度均匀密网格模拟网格规模为40.32 万,可见自适应模拟节省了约90%的计算量.

图20 有限尺寸弯道爆轰传播问题不同时刻压力和网格分布 (左:整体流场压力分布,中:局部放大压力分布,右:局部放大网格分布)Fig.20 Simulation results for detonation problem in finite-size curved pipeline (left:pressure distribution,middle:local enlarged pressure distribution,right:local enlarged mesh distribution)
4 结论
本文针对爆轰驱动多介质问题的高分辨率健壮数值模拟需求,提出了适应于爆轰弹塑性多介质Lagrange 流体力学程序的非结构网格多层自适应加密与稀疏技术,在发挥非结构多层自适应数据结构灵活性优势的基础上,通过将有效网格压至一层进行Lagrange 计算,避免了Lagrange 框架下多层网格分别计算带来的层间耦合困难.更进一步地,实现了Lagrange 多层AMR 与接触滑移算法的自适应耦合,使其对包含复杂几何边界的多分区、多介质问题有很好的适应性.采用上述AMR 方法,实现了拐角爆轰、多层炸药隔爆、有限尺寸弯道爆轰等多个复杂多介质、多分区问题的Lagrange 多层AMR 模拟,获得了丰富的凝聚炸药爆轰与弹塑性介质相互作用的流场图像.
后续工作将针对凝聚炸药爆轰与惰性金属材料相互作用规律开展深入系统的研究,包括本文涉及的复杂爆轰驱动多介质问题的计算条件和物理模型参数的定量标定,在此基础上获得不同炸药、不同约束材料和不同几何构型下爆轰约束效应及其非理想行为的规律性认识.

