一种城市路网多层次复合网格模式识别方法

王安东,武 芳,巩现勇,翟仁健,刘呈熠,邱 越,张寒雪

信息工程大学地理空间信息学院,河南 郑州 450001

城市道路网是城市范围内不同功能、等级、区位的道路,以一定密度和适当形式组成的网络结构[1]。作为城市的基础骨架,其结构模式体现了城市的主要结构和空间格局,反映出城市的地形地貌特点、功能结构和规划治理情况,蕴含着大量城市形成和发展的内在机制[2]。对其结构模式的挖掘和识别是地图综合、城市形成、更新和扩张、交通规划设计等领域的研究热点和难点[3-5]。

相关研究从不同研究重点出发,将道路网分为不同结构模式,如网格模式、环型模式、放射型模式、复杂道路交叉口等显式模式[6-11],以及城市中心、热点区域、城市建成区等隐式模式[12]。网格模式作为城市道路网的典型结构模式,在城市布局中十分常见,在长达几千年的城市发展史上,都得到广泛的采用[13]。道路网格模式的识别对城市空间特征挖掘、交通规划及地图自动综合具有重要意义。根据识别的基本模式单元,现有道路网格模式的识别方法可大体分为两类。

(1) 基于路段的识别方法。此类方法多将道路网抽象为图结构,以图中顶点作为基本处理单元,从顶点的几何、上下文关系特征中抽象出与路网结构相关的特征项,借助图论、统计学或机器学习方法进行处理或学习,实现网格模式识别。例如,基于道路结点和改进的霍夫变换策略来实现规则格网的识别[14];通过构建道路网对偶图,采用交、并、联合等图运算来提取基础格网模式[15];基于道路结点的几何、拓扑特征,利用多项式评定模型识别道路网中的典型结构模式[16];基于道路网的线性单元剖分,提出5种特征参量,采用支持向量机分类来提取网格模式[17-18];在构建道路网原始图的基础上,利用图卷积神经网络模型,通过学习人工标注样本,实现网格模式的识别[19]等。

(2) 基于网眼的识别方法。此类方法将道路网中路段围成的闭合区域转化为面,即道路网眼,通过计算网眼与邻近网眼的形状、方向、尺寸相似性及排列特征,采用邻近搜索、任务分类、隶属度计算或自组织映射聚类等方法完成网格模式的识别。例如,通过计算网眼的几何特征相似性,采用区域生长算法识别网格模式[20-21];基于网眼的形状和关系描述参量,采用机器学习算法识别网格模式,以减少参数阈值设置的人工干预[22-25],等。

然而,当前研究中至少存在如下问题有待解决:①根据定义,道路网格模式的基本特征是由两组几乎平行的道路垂直相交构成,网眼形状大多为近似矩形或平行四边形。然而,基于路段的识别方法大多以道路网结构中的“正交性”原则为依据,设计网格模式的特征因子,忽略了网格模式中相邻网格间的尺寸、形状相似性和分布的延伸性。从结构模式的定义来看,这些研究的部分识别结果更接近于道路网的“正交模式”或“方格模式”,而非“网格模式”。②基于网眼的已有识别方法均以单个网眼面要素及相邻网眼间“一对一”的邻近关系作为研究对象,对于整体规则、局部破碎的网眼群组,无法将其作为一个整体参与模式构建。

为了解决具有局部异质性的道路网格模式识别问题,本文基于道路网眼,顾及视觉认知的层次性,提出一种城市道路网多层次复合网格模式的识别方法,主要解决两个问题:①道路网眼分布模式的多层次认知特征和定义;②网眼复合直线模式和复合网格模式的识别。

1 道路网眼分布模式的多层次认知特点

道路网眼是指道路网中路段围成的闭合区域。与其他面状地图要素相似,道路网眼群组具有丰富的分布模式,直线模式和网格模式是两种典型的分布模式。直线模式中道路网眼有规律地呈直线分布,网眼间具有相似的几何特征,如方向、尺寸等;网格模式由若干组近似平行的直线模式与另外若干组近似平行的直线模式,以近似正交的方式相交构成。作为道路对空间划分的结果,其分布模式与道路结构模式有着密切联系。道路网眼的直线和网格模式是道路网格模式的两种表现形式,图1中模式1、2分别为网眼的直线和网格模式,两组模式均表现为道路网的网格模式。因此,本文以道路网眼为基本模式单元,通过提取其直线和网格模式,实现道路网格模式的识别。

图1 道路网结构模式与网眼分布模式

依据格式塔认知准则[26]和“大范围优先”的视知觉认知理论[27-28],人类更倾向于以“主体→细节”的顺序来认知事物。道路网眼群组具有丰富复杂的几何、拓扑特征,人类的认知过程也必然遵循一定的顺序,从而形成了其空间关系的层次性。观察者观看地图时,首先关注道路网眼的整体特征,如图2(a)红色方框中网眼整体具有明显的网格模式特征;然后,才会注意到局部网眼间的细节特征,如图2(b)所示,蓝色网眼间的几何形态差异和复杂拓扑关系会被进一步感知。然而,当前相关研究仅考虑相邻单个网眼间的“一对一”关系,难以识别由多个不规则的网眼多边形拼接而成的网格网眼,对于大比例尺地图中局部异质性明显的道路网格模式,识别结果并不符合人类认知[29]。

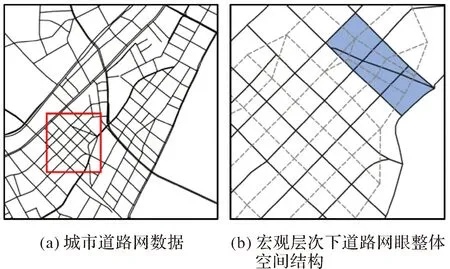
图2 整体到局部的认知过程

为解决网格模式中局部网眼破碎的问题,本文引入“复合道路网眼”的概念。复合道路网眼的直线和网格模式具有多层次认知的特点:宏观尺度下,道路网眼整体呈直线或网格模式分布;中观尺度下,模式由几何特征相似、排列规律相近的简单或复合矩形网眼构成;微观尺度下,根据简单网眼的组合方式,复合矩形网眼进一步划分为包含关系和并列关系复合网眼。复合道路网眼直线和网格模式的多层次认知关系如图3所示。以图4(a)中道路网为例,各层次的具体含义如下。

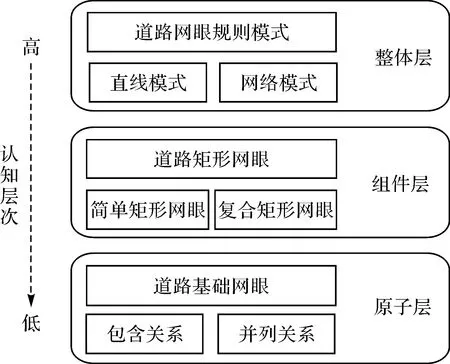
图3 道路网眼多层次认知关系

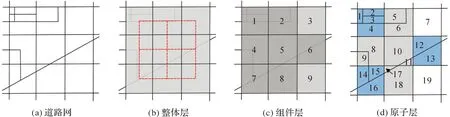
图4 多层次认知过程

(1) 整体层,包括直线模式和网格模式,其中直线模式的识别是网格模式识别的前提和保障。网眼直线模式具有以下的表现形式:①模式内部的各个网眼具有相似的形状、大小和方向特征;②模式内相邻网眼方向一致,且模式的全局方向与各网眼组件方向近似相同或正交;③模式内相邻网眼的公共边近似为两最小面积外界矩形的长边或短边,图4(b)中红色虚线分别表示呈直线模式分布的网眼。网格模式由多组直线模式近似垂直相交构成,处于更高的认知层次,如图4(b)中9组直线模式以近似正交的方式相交构成网格模式。

(2) 组件层,构成单元为近似矩形的道路网眼。根据矩形网眼所中的基础网眼数量,分为简单矩形网眼和复合矩形网眼,分别如图4(c)中网眼3、9和网眼1、2、4、5、6、7、8。其中,简单矩形网眼形状为近似矩形;复合矩形网眼包含多个任意形状的道路网眼,组合后形状为近似矩形。从矩形网眼与基础网眼的空间对应关系的角度来看,组件层中包含1∶1(简单网眼)和1∶n(复合网眼)的空间对应关系。

(3) 原子层,构成单元为由道路网结点、路段直接围成的封闭区域多边形,即简单网眼。根据邻接关系,将组件层复合网眼中简单网眼间关系划分为包含关系和并列关系。包含关系复合网眼由一个主体网眼和若干次要网眼组成,如图4(d)中灰色网眼5、6,网眼8、9,网眼10、11和网眼17、18。主次网眼间空间邻近,整体轮廓互补。其中,主体网眼的面积相对较大,在视觉认知中占主导地位,反映该复合网眼的主要形状特征,如图4(d)中网眼6、8、10和18;次要网眼的面积相对较小,在视觉认知中占从属地位,如图4(d)中网眼5、9、11和17。并列关系复合网眼由若干简单网眼组成,网眼为任意形状多边形,组合后形状为近似矩形,并与相邻网眼构成直线模式。网眼间并列关系难以通过自底向上的组合方法进行探测,其关系的识别依赖于复合网眼邻域的模式特征。图4(d)中蓝色网眼1、2、3、4,网眼12、13和网眼14、15、16分别为具有并列关系的简单网眼。

2 道路网多层次网格模式识别

结合道路网眼的多层次认知特点,本文采用自底向上与自顶向下相结合的策略,提出一种多层次道路网眼直线和网格模式的识别方法,整体框架如图5所示,基本思想和关键步骤如下。

(1) 根据视知觉感知理论中完整性、规则性等心理倾向,采用自底向上的策略,合并具有包含关系的网眼,将整体规则、局部不规则的相邻网眼组合为视觉感知上更高级的复合网眼。

(2) 考虑相邻网眼间的尺寸、形状相似性和分布的直线性,构建直线模式结构化参数,以此为约束提取直线模式。

(3) 根据直线模式分布的延伸性,自顶向下构建直线模式连续匹配模板,搜索合并直线模式两端具有并列关系的道路网眼,实现复合直线模式的提取。

(4) 采用降维的思想,将直线模式网眼组以二维的线段表示,对其进行分解和组合,实现道路网眼网格模式的提取。

道路网眼形状为近似矩形是其作为直线和网格模式的组成单元的必要条件[20-24]。本文采用矩形度(Rec)和凹凸度(Conv)[29]作为网眼矩形相似度的度量参数,具体含义与计算方法见表1。

表1 网眼矩形相似度的度量参数

2.1 简单直线模式识别

简单直线模式由当前数据中的简单网眼构成,其正确识别是复合直线模式识别的基础。考虑直线模式中网眼的相似性、直线性和延伸性等结构特征,结合格式塔认知准则,从道路网眼的大小相似性、直线性和对齐程度3个方面引入识别道路网眼直线模式的结构化参数(表2)。

表2 网眼直线模式结构化参数

根据直线模式的组织规律,同一模式内部要素间具有相似的几何形态结构。对于道路网眼,其几何形态结构主要表现为形状和大小。其中形状依靠上文中矩形相似度参数进行约束;大小相似度利用网眼面积比进行度量,面积比越大,网眼间大小相似程度越高。为保证模式中的网眼沿直线分布,以表2中方向差异参数作为约束,方向差异Dorient越接近于180°,模式的直线性越强。考虑到直线模式相邻网眼间具有相互对齐的特点,引入公共边长度比Rce对模式内相邻网眼间对齐程度进行约束。如图6所示,对于相邻网眼M1、M2,定义其公共边长度比(Rce)1,2为公共边(P1P2)长度与公共边对应网眼最小外接矩形边(EM1、EM2)长度的比值的较小值,公共边长度比越接近于1,网眼对齐程度越高。

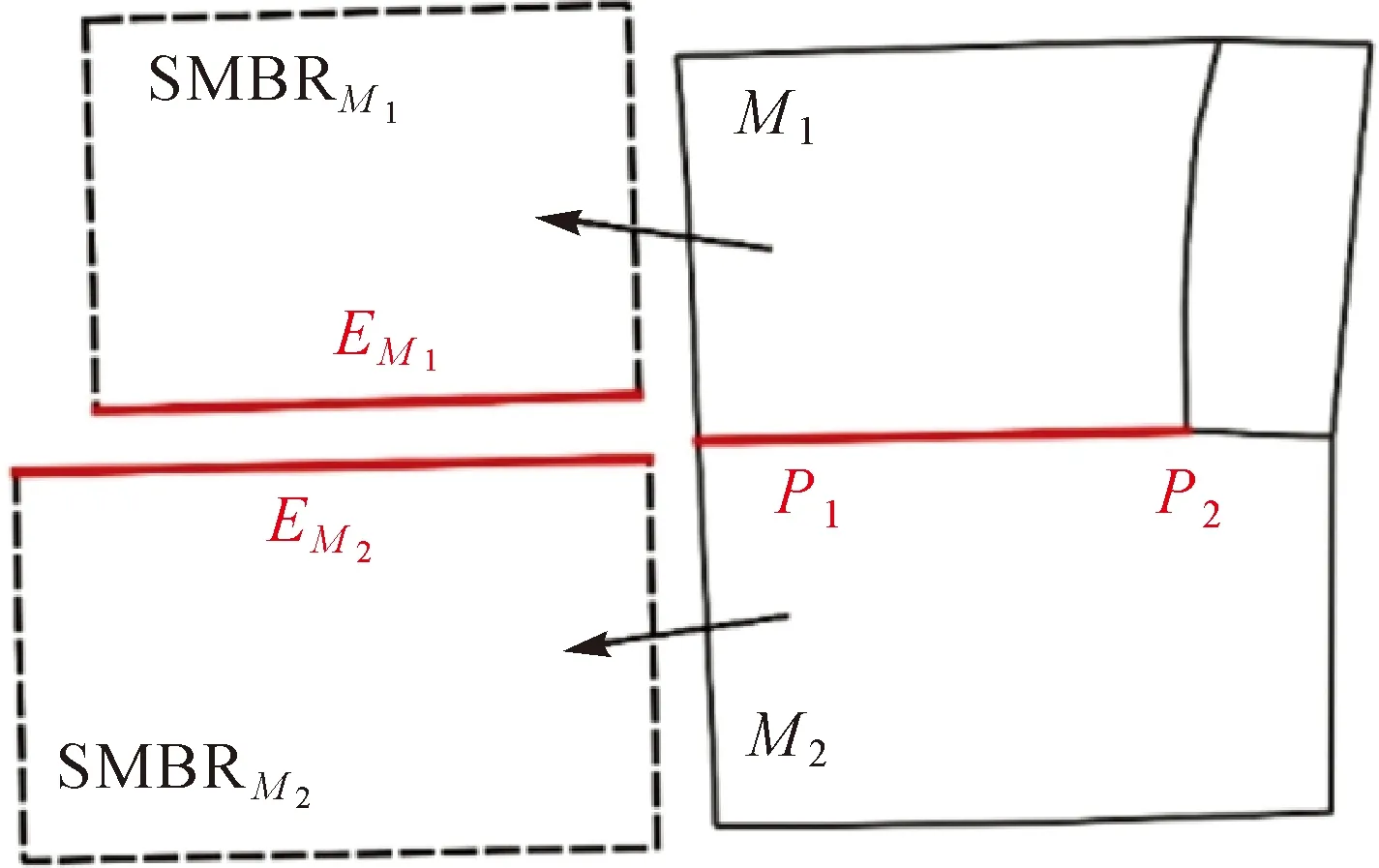
图6 公共边长度比

综上,本文识别网眼简单直线模式的步骤如下。

步骤1:根据网眼间是否具有公共边,构建相邻网眼间邻近关系,同时提取网眼群中矩形度和凹凸度分别大于阈值δRec和δConv的简单矩形网眼,加入列表ListSGM。

步骤2:选取ListSGM中任一网眼Mi及其邻接网眼Mj,计算Mi与Mj的面积比(Rarea)i,j和公共边长度比(Rce)i,j,若(Rarea)i,j>δarea且(Rce)i,j>δce(式中δarea和δce分别为人工设定的面积比和公共边长度比参数阈值),则将网眼Mi与Mj的邻近边ei,j加入直线模式临时列表tListLP,否则,返回步骤2。

步骤3:设当前直线模式一侧搜索方向为{i,j},即SearchLeft={i,j},另一侧搜索方向为{j,i},即SearchRight={j,i},以SearchLeft={i,j}为起始搜索方向,选取Mj的邻接网眼Mk,若Mj除Mi不存在其他邻近网眼,则此搜索方向终止,以SearchRight={j,i}方向继续搜索。

步骤4:计算Mj与Mk的面积比(Rarea)j,k和公共边长度比(Rce)j,k,若(Rarea)j,k>δarea且(Rce)j,k>δce,则执行步骤5,否则,返回步骤3。

步骤5:计算Mi、Mj、Mk的方向差异Dorient,若Dorient>δorient,则将ej,k添加至当前直线模式列表tListLP中,并令j=k,否则,返回步骤3。

步骤6:若当前直线模式向两侧搜索均终止,则该组直线模式识别结束,将当前直线模式列表tListLP加入直线模式识别结果列表ListLP中,返回步骤2。循环步骤2—6,直至ListSGM中全部网眼均被遍历。

以图7(a)中道路网数据为例,经上述步骤识别的网眼简单直线模式如图7(b)中红色线段所示。受道路网中较低等级道路影响,一些在大尺度上认知为整体的网眼被分割成若干小网眼,呈现出局部破碎的现象,如图7(b)中网眼1、2、3。由图7(c)中网眼邻近关系可以看出,简单直线模式的提取方法仅利用简单网眼间“一对一”的邻近关系(蓝色线段),难以反映道路网的整体结构模式,需要进一步利用复合直线模式识别方法,提取局部破碎、整体规则的直线模式。

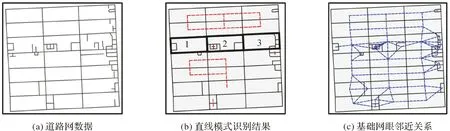
图7 道路网眼简单直线模式识别结果

2.2 复合网眼构建与复合直线模式识别

复合直线模式的识别是解决网眼局部异质性,实现由低级基础网眼到高级认知模式过渡的关键,其难点在于组件层中复合矩形网眼的识别和构建。对于复合矩形网眼中的包含关系和并列关系,本文分别采用自底向上和自顶向下的策略对其进行识别。

2.2.1 包含关系识别

根据包含关系网眼间轮廓互补的特点,参考文献[30]中对相离面要素主次关系识别的方法,引入公共边长周长比(Rlength)和约束面积比(Rca)两个参数,分别从一维和二维两个维度描述相邻网眼之间的包含程度。以图8中道路网眼为例,红色线段P2P3P4表示相邻网眼M1、M2间公共边,虚线矩形为M2最小面积外接矩形SMBRM2,灰色多边形P1P2P3P4为SMBRM2与M1的公共区域多边形,参数含义及计算方法见表3。

表3 包含关系识别参数

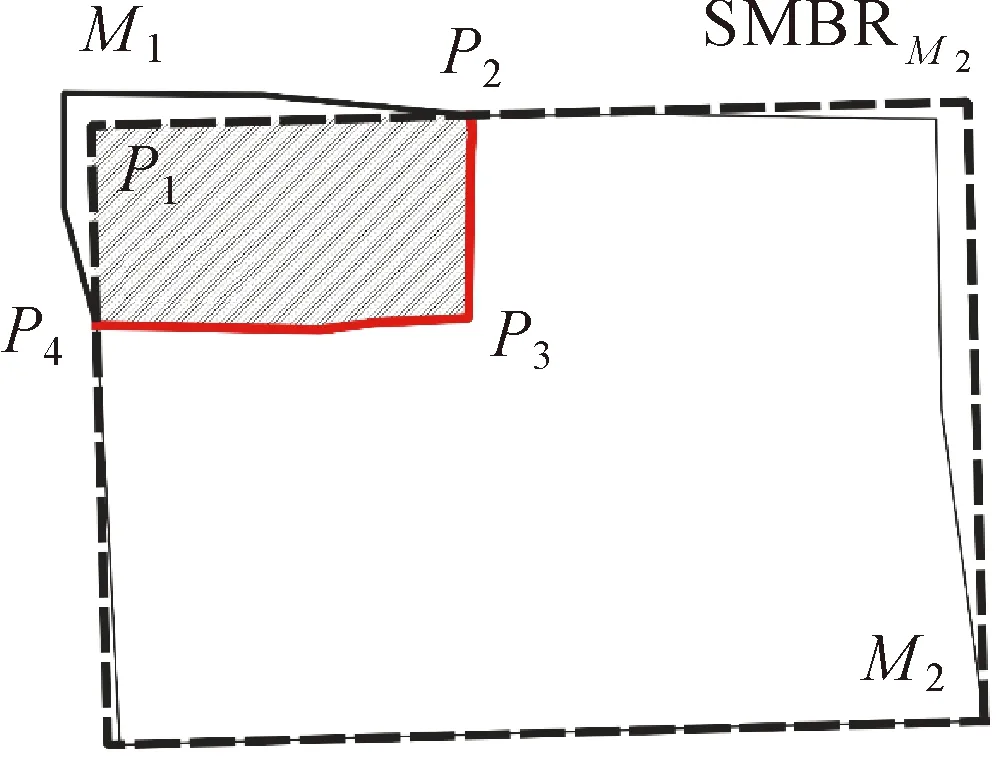
图8 包含关系参数

根据包含关系参数和网眼矩形相似度参数,识别包含关系复合矩形网眼的步骤如下。

步骤1:计算网眼矩形度Rec和凹凸度Conv,将Rec<δRec或Conv<δConv的网眼加入列表mList中。从中选取网眼Mi,计算其与邻近网眼Mj的公共边周长比(Rlength)i,j和约束面积比(Rca)i,j,若(Rlength)i,j>δL且(Rca)i,j>δca,则将网眼Mi和Mj记为包含关系组,其中δlength和δca分别为人工设定的公共边周长比和约束面积比参数阈值。

步骤2:合并网眼Mi与Mj,记新网眼为Mn,若Recn>δRec或Convn>Convi,说明次要网眼对主要网眼的规则程度具有补充作用,将Mn加入列表mList中,并从中删除Mi和Mj,否则删除Mn。

步骤3:循环步骤1、2,直至列表mList中的元素数量不再减少为止,此时全部具有包含关系的复合矩形网眼均被识别。

以图7中道路网眼为例,利用上述步骤识别、合并包含关系网眼的过程如图9所示。图9(a)为步骤1包含关系的识别结果,粉色线段表示网眼间的包含关系。图9(b)为步骤2包含关系第一次合并结果(深色网眼),粉色线段表示所产生的新的包含关系。经数轮迭代,具有包含关系网眼的最终合并结果如图9(c)所示,其中深色网眼为合并后的包含关系复合网眼。

图9 包含关系复合网眼识别与合并过程

2.2.2 并列关系识别及复合直线模式提取

从认知角度来看,并列关系复合网眼产生于邻域内直线模式的延伸,例如对于图9(c)中邻近关系相似的网眼对1、2和2、3,网眼1、2更容易被组合为复合网眼。因此,本文利用网眼邻域的模式特征,采用自顶向下的匹配策略,识别具有并列关系的复合网眼。基本思想为:首先根据直线模式两端网眼确定初始匹配模板的几何特征;然后结合直线模式延伸性构建连续匹配模板,向两端搜索、匹配待识别网眼;最后结合直线模式约束条件,判定待识别网眼组合后能否构成直线模式,实现复合直线模式的提取。结合图9(a)中道路网眼,说明并列关系及复合直线模式识别方法的具体步骤。

步骤1:合并具有包含关系的矩形网眼(图9(c)),提取简单直线模式(图10(a)中红色线段),存入SLPList中。

图10 并列关系网眼与直线模式识别过程

步骤2:选取任意一组直线模式SLPi(图10(a)中红色加粗线段),提取其首、末端网眼的最小面积外接矩形,以首、末端网眼与其邻接网眼几何中心的相对距离d、方向o为约束,沿直线模式两端延伸方向计算匹配模板的位置,匹配模板分别记为Tl、Tr(图10(a)中蓝色矩形)。

步骤3:搜索与Tl和Tr存在面状交集的网眼,记为Ms,如果其模板重叠度(Rto)s,l>δto或(Rto)s,r>δto,则将Ms存入并列关系候选列表MList中,执行步骤4,否则,则执行步骤2,式中δTC为人为设定的模板重叠度参数阈值。

步骤4:若Mlist中网眼数量大于1,合并MList中全部网眼,记为Mn,如图10(b)中蓝色网眼,若Rec(Mn)>δRec,则根据2.1节中方法,判断其能否满足直线模式结构化参数约束,若满足,执行步骤5,否则终止该侧搜索。

步骤5:当直线模式SLPi向两侧搜索均终止时,将其存入复合直线模式列表MLPList,并从SLPList中移除,执行步骤2。循环步骤1—5,直至SLPList为空时,结束循环。识别结果如图10(c)所示,其中红色线段表示网眼直线模式。

2.3 网格模式提取

道路网眼的网格模式由近似正交的直线模式相交构成,处于更高的认知层次。由网格模式概念可知,组成网格模式的直线模式之间需满足以下3项条件:①各组直线模式近似平行或正交;②正交的直线模式间具有相交关系;③各直线模式构成闭合回路。

对于条件①,由于在直线模式中,网眼为方向一致的近似矩形,网眼构成的直线模式方向基本确定,若任意两组直线模式包含同一网眼,则其关系为近似正交;若任意两组不相交直线模式间,存在其他直线模式同时包含以上两组直线模式中的网眼,则两组直线模式近似平行。故条件①可由条件②代替。另外,若多组直线模式构成闭合回路,则相互正交的直线模式间必然相交,故条件③为条件②的充分条件。

综上,本文通过对直线模式网眼构成闭合回路进行识别,提取其中的网格模式。当前研究大多采用图论中算法识别多组直线模式中的闭合回路[31-32],算法实现较为复杂。本文从几何角度出发,通过对直线模式邻近图中由结点和线段形成的封闭多边形进行聚类,实现网格模式的提取。以图11(a)道路数据为例,说明算法具体步骤。

图11 网格模式提取过程

步骤1:以各直线模式中网眼几何中心为结点,依次连接相邻网眼,构建直线模式关系图Gl(图11(b)中红色线段)。

步骤2:提取Gl中封闭区域多边形P(图11(b)中晕线多边形P1、P2、P3),将其存入列表TPList。

步骤3:遍历TPList,若两多边形Pi、Pj间存在公共边(图11(b)中多边形P2、P3),则将其聚类为一组,存入列表ClusterList中。

步骤4:根据聚类结果,提取每组聚类内多边形顶点所对应的道路网眼,记为一组网格模式网眼Gridm,存入Grid_list中,如图11(c)中蓝色和黄色线段对应网眼分别为两组网格模式。

3 试验与讨论

3.1 试 验

本文基于Python和QGIS编程实现以上算法。试验分为两组,数据分别采用不同空间结构模式的国内外道路网数据。试验中网眼矩形度和凹凸度阈值的设置影响简单矩形网眼以及包含关系、并列关系的识别,结合前人的研究成果[29,33],取δRec=0.9、δConv=0.95。算法中所涉及其他阈值设置的指导思想为:面积比和公共边长度比的阈值越大,方向差异的阈值越小,模式的直线性越强。在识别包含关系矩形网眼时,公共边周长比和约束面积比的阈值越大,主要网眼对次要网眼的包含程度越强;在识别并列关系矩形网眼时,模板重合度的阈值越大,模式的同质性越强。

试验区域1为国外某地区道路网,数据来自OpenStreetMap。如图12所示,所选试验区域内道路分布密度较高,密度不均匀,没有全局平稳的特征,存在支离破碎的短小路段,但大部分呈垂直交错结构分布,视知觉上呈现出明显的网格模式特征。试验区域包含2469个道路简单网眼。经反复测试,试验参数设置见表4。图12(b)中灰色和蓝色网眼分别为识别出的具有包含和并列关系的复合网眼,提取的直线模式和网格模式分别如图12(c)、(d)所示。

表4 参数阈值设置

试验区域2为郑州市三环内道路网,数据来自OpenStreetMap。如图13所示,所选试验区域道路分布密度较高,且不均匀,存在显著的空间异质性,整体上没有平稳的全局结构特征,但在局部区域内呈现出明显的网格模式。试验区域包含6828个道路网眼。试验参数设置见表4。图13(b)中灰色和蓝色网眼分别表示识别出的具有包含和并列关系的复合网眼,提取的直线模式和网格模式分别如图13(c)、(d)所示。

图13 试验2直线模式和网格模式识别结果

为验证本文方法的有效性,选用道路网简单网格模式的提取方法作为对比试验[20],识别结果及试验结果细节对比如图14所示,其中蓝色与红色线段分别表示对比试验与本文方法的识别结果。由于只有自身呈矩形,周围不存在与之相似网眼的道路网眼不属于网格模式[15],为对其进行区分,本文将试验结果中的网眼划分为矩形网眼和网格网眼。其中,矩形网眼为形状近似矩形的网眼,而网格网眼除满足矩形网眼要求外,还作为模式单元构成道路的网格模式。另外,根据网眼的组成方式,将矩形和网格网眼按简单网眼和复合网眼进一步划分,其中复合网眼包括包含关系复合网眼和并列关系复合网眼。试验1、2及其对比试验各类网眼数量统计结果见表5。

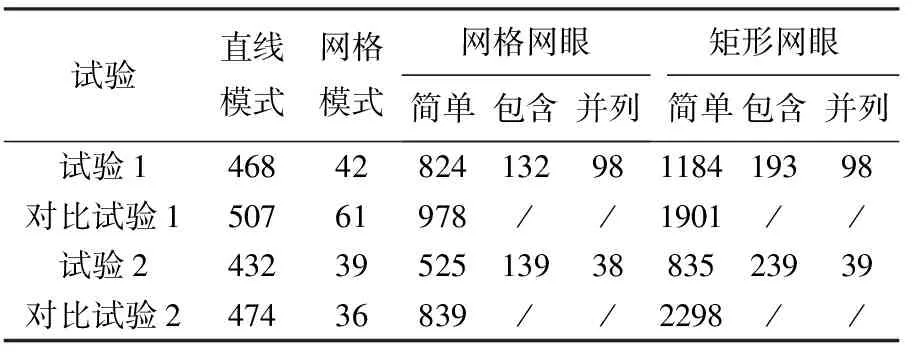
表5 试验结果统计

图14 试验结果细节对比

进一步地,计算试验1、2及对比试验中的网格网眼面积,统计结果箱线图如图15所示,其中箱体上下端线段分别表示面积上、下四分位数,箱体中部线段表示面积中位数。

图15 网眼面积箱线图

结合试验结果对比及统计结果,分析可知,本文方法能够有效识别简单网眼间的包含和并列关系,提取出尺寸更大、面积分布更集中的复合网眼(图15中本文方法箱体整体均高于对比方法且箱体长度小于对比方法),并以此为基础,识别道路网格模式。相较于对比方法,本文方法识别结果具有更好的层次性、整体性和连续性。

为了验证本文方法的可靠性,对试验结果进行定量评价,采用目视判别的方式标记试验区域数据中的网格网眼,以正确分类网眼数量与网眼总数量之比作为准确率,以正确分类网眼数量与识别的网格网眼数量之比作为召回率,两组对比试验的评价结果见表6,结果表明本文方法的识别结果是可靠的。

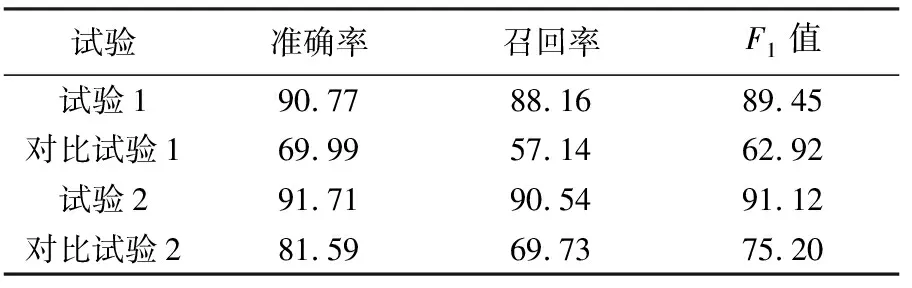
表6 试验结果准确率、召回率和F1值

3.2 讨 论

(1) 参数阈值。对于不同类型模式而言,阈值主要根据模式的结构特征确定。对于同一种模式,由于数据的尺度、空间分布情况存在差异,阈值可能会在一定范围内进行调整,但必须符合模式的视觉认知特征。因此,对于不同数据,参数阈值不会发生太大变化。本文参数阈值的设置主要以相关研究中的经验值为主,同时结合试验进行微调。以直线模式结构化参数为例,由于在人类对道路网格模式感知过程中,相邻网眼间方向和对齐特征对认知的影响远超尺寸相似性特征。图16(a)、(b)、(c)分别为面积比阈值分别取0.6、0.7、0.8的识别结果。对比发现,随着面积比阈值的增大,面积差异较大的网眼间直线关系被剔除,导致模式退化。公共边长度比阈值的选择直接影响模式的对齐特征。仅考虑公共边长度比,忽略其他因素对模式的影响,图16(d)、(e)、(f)分别为公共边长度比阈值取0.92、0.85、0.78的识别结果。对比发现,随着公共边长度比阈值的放宽,直线模式中相邻网眼间对齐程度逐渐降低。因此,本文试验中面积比阈值设置相对较小,而公共边长度比阈值设置相对较大。

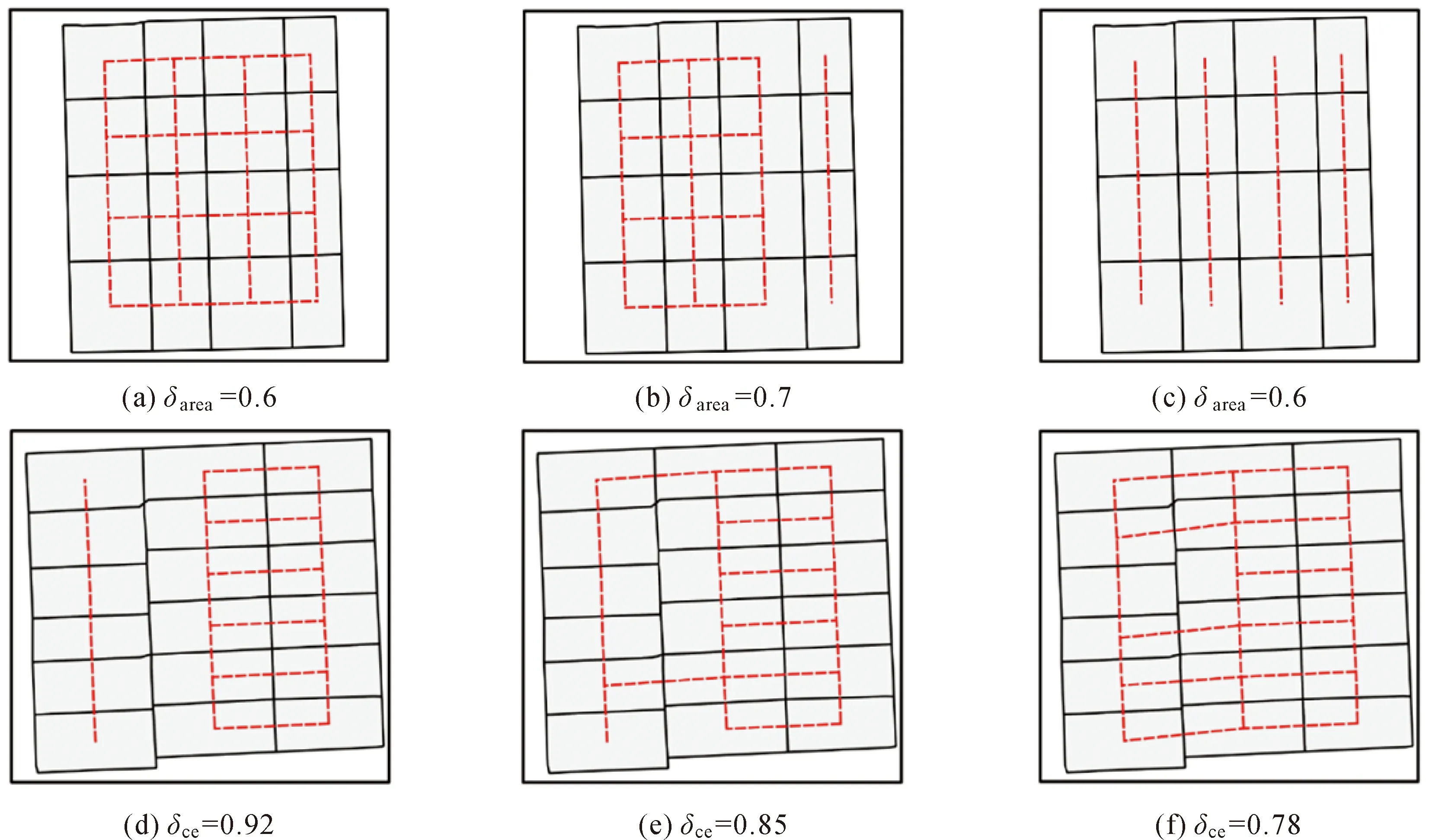
图16 参数阈值设置影响

(2) 多线道路的约束。在现势性较好的大比例尺城市地图数据源中,大部分快速路、主干道呈双线或多线模式,导致同一条路段内部出现一个或多个网眼,如图17中黄色网眼。由于面积、形状存在显著差异,这类网眼对于基于相邻网眼相似度和一致性的网眼模式而言,具有明显的约束作用。例如图17(a)中,郑州市主干道航海路所对应黄色网眼将该区域内网眼划分为模式A和模式B,该结果符合高等级道路对低等级道路模式的约束作用。然而除主干道外,部分低等级道路同样以双线道路表示,如图17(b)中黄色道路网眼,导致模式断裂。实际应用中,可根据需求,对双线或多线道路的重要性分级,以中心线表示等级较低的双线道路,以获得更为准确的识别结果。

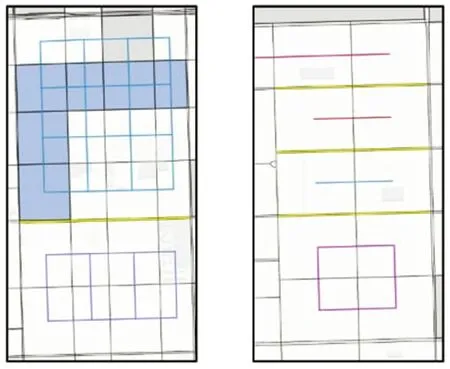
图17 双线道路约束作用

(3) 与基于路段方法对比。除试验1、2中的对比试验外,以基于路段的道路网格模式识别方法[32]作为对照,讨论本文方法在大比例尺道路数据网格模式识别中的优势。图18为试验2中部分数据采用基于路段方法的网格模式识别结果(图18(a)中深蓝色路段)与本文方法的识别结果(图18(b)中深红色线段)。基于路段的识别方法以相连路段间正交关系为约束条件,通过搜索道路网中的网格回路,实现网格模式的提取。对比可知,该方法识别结果中,网格模式路段之间的形态差异大、粒度大小不一且不具备稳定性和连续性,其结果更接近于“方格模式”或“正交模式”,而非“网格模式”。而本文方法能够克服局部低等级道路对整体结构模式的影响,基本解决了基于网眼识别网格模式方法中“图形-背景”难以区分的问题[24],有效提取出与人类认知相符的网格模式,识别结果中,网眼的形态结构和粒度大小一致性较高。进一步地,本文方法在直线模式识别的基础上,实现了对网格模式的聚类分组,与现有方法相比,本文方法的识别结果对地图综合、城市街区划分及功能区识别等后续应用具有更高的指导价值。

4 结 论

由于大比例尺地图数据中存在大量等级较低的道路路段,导致中宏观尺度下道路网格模式在微观尺度下呈现整体规则、局部破碎的结构特征,现有方法尚不能有效提取其中的网格模式。本文以道路网眼为切入点,首先分析了道路网眼的多层次认知特点,引入了复合网眼直线模式和网格模式的定义。通过自底向上和自顶向下的策略挖掘简单网眼间的包含关系和并列关系,克服了现有方法仅针对网眼间一对一关系的不足,为网眼复合直线模式和网格模式的识别提供支撑。然后利用结构化参数实现网眼复合直线模式的识别。最后根据其垂直相交的特点,提取网眼的复合网格模式。识别结果更符合人类认知,对道路网数据的多尺度表达具有理论和实用价值。

今后工作中需要进一步研究的问题包括:①分析不同尺度及空间分布特点的道路数据对本文方法中各项参数阈值的影响;②结合道路语义、等级层次性,研究其在不同尺度下对道路结构模式的影响;③探索道路复合网格模式提取结果在地图制图综合中的应用。