基于网络流与危险与可操作性分析的天然气站场系统可靠性

周娇, 于安峰*, 郭俊吕, 凌晓东,3, 姜雪,3, 刘金玲,3, 胡川,3

(1. 中石化安全工程研究院有限公司化学品安全控制国家重点实验室, 青岛 266000;2. 中国石油天然气股份有限公司广东石化分公司, 揭阳 515200;3. 中石化国家石化项目风险评估技术中心有限公司, 青岛 266071)

天然气站场在气田地面系统中起着关键节点的作用,其主要任务是汇集上游来气,通过节流调压、分离、计量、增压等工艺流程后输入集气干(支)线送至下游处理厂净化处理后外输。长期的高压、腐蚀条件必然会对站内的设备和管道造成一定程度的腐蚀和损坏,一旦设备发生故障,不仅会造成生产中断,还会造成燃烧爆炸事故,极易造成人员伤亡、环境污染等严重后果,因此,天然气站场的安全稳定运行已成为气田安全生产的重要环节,对天然气站场系统进行可靠性分析势在必行。同时,在危险与可操作性分析(hazard and operability analysis,HAZOP)下,天然气站场在工况调整时,不同偏差状态下其可靠性明显不同,高风险状态下的站场运行状态显著影响站场的整体可靠性,因此对于高风险状态下的站场系统可靠性分析也十分重要。

然而中国的可靠性研究相对于国外起步较晚,且在油气储运工程领域更多的是在管道可靠性研究上,在站场系统可靠性方面的研究较少。邢尚鹏等[1]、廖柯熹等[2]总结了设备与管道的可靠性评估方法,主要通过故障树分析、蒙特卡洛模拟方法探讨设备与管道的可靠性,评估结果可以降低运行风险。胡钧铭等[3]、周洁等[4]建立了基于模糊层次分析法、故障树算法的设备可靠性分析模型,对专家语言进行量化处理。姚东池[5]基于贝叶斯理论计算脱水脱烃站内主要设备的可靠性参数。吴云冬[6]基于经典基于风险的检验(risk based inspection,RBI)理论和设备失效统计数据,建立了基于威布尔分布函数的同类失效概率修正模型与损伤因子修正模型,基于图论最小割集理论分析了高含硫天然气集输站场网络系统的失效概率。王鹤男[7]采用动态故障树(dynamic fault tree,DFT)法,将逻辑门转化为马尔可夫链,并采用威布尔分布函数对其进行改进,计算出成品油站场冗余单元的失效概率。根据以上调研情况可以看出,国内学者在关于站场系统可靠性的研究中,几乎都是应用的经典RBI理论作为可靠性的分析基础,站场拓扑结构也是采用串并联的基础分析方法,没有将站场系统进行整体的网络分析,也并没有提出高风险状态下的系统整体可靠性分析,因此亟须新的方法来进一步拓展天然气站场系统可靠性分析领域。

现将常用于风、电系统的网络流理论应用到天然气站场系统的可靠性分析中,并对网络流理论做了归纳创新与适应性分析,提出网络流分步法与网络流整体法的概念,方法可直接分析系统整体,比分单元分析后再系统分析的传统图论方法更简洁、更直观。之后创新性地提出基于HAZOP分析确定站场系统在工艺参数偏差状态下的失效概率,分析偏差状态对于站场系统可靠性的影响,将其与正常工艺状态下的站场系统失效概率对比,从而更加全面地分析天然气站场系统的整体可靠性。

1 研究方法

研究方法主要是网络流理论与基于HAZOP分析的工艺参数偏差状态下的站场系统可靠性分析。其中网络流理论是站场系统可靠性分析的整体框架方法,最小路集分析是基于网络流理论求解站场系统失效概率的方法,不交化算法是避免求解最小路集时出现“维数爆炸”问题的优化算法。基于HAZOP分析的工艺参数偏差状态下的站场系统可靠性分析则是对于站场系统在非正常工况下的可靠性分析,主要研究思路如图1所示。

图1 研究思路图Fig.1 Research idea map

1.1 网络流理论适用性分析

网络流图是一种能很好地反映网络特性的模型,因为无论网络结构多么复杂,其都能清晰地显示组织结构和逻辑关系。根据流体流动方向,将网络流图分为无向图和有向图[8]。同时,将网络流用于站场系统可靠性分析中的明显优势是站场系统的网络流可靠性分析既可整体分析也可分单元分析,将整个系统可看作一个网络,分析过程简化。

在进行站场系统可靠性分析时,设备(含阀门)视为图中的节点,管道表示为边,所有的设备(含阀门)和管道构成的集合就表示了站场网络中所有单元。为了分析研究站场系统的可靠性,根据设备(含阀门)和管道的失效概率来设置点与边的权重,进而计算出整个站场系统的失效概率。

由网络流理论可知,图G可以由集合形式来表示,即

G={V,E}

(1)

式(1)中:V={v1,v2,…,vi,…,vn}为G的节点集;E={e1,e2,…,ei,…,en}为G上的节点连接关系,称为G的边集,边集中的边都能由点之间的关系来表示,即

ei=(vs,vt),ei∈E;vs,vt∈V

(2)

图2中,其节点集和边集的表示如下:

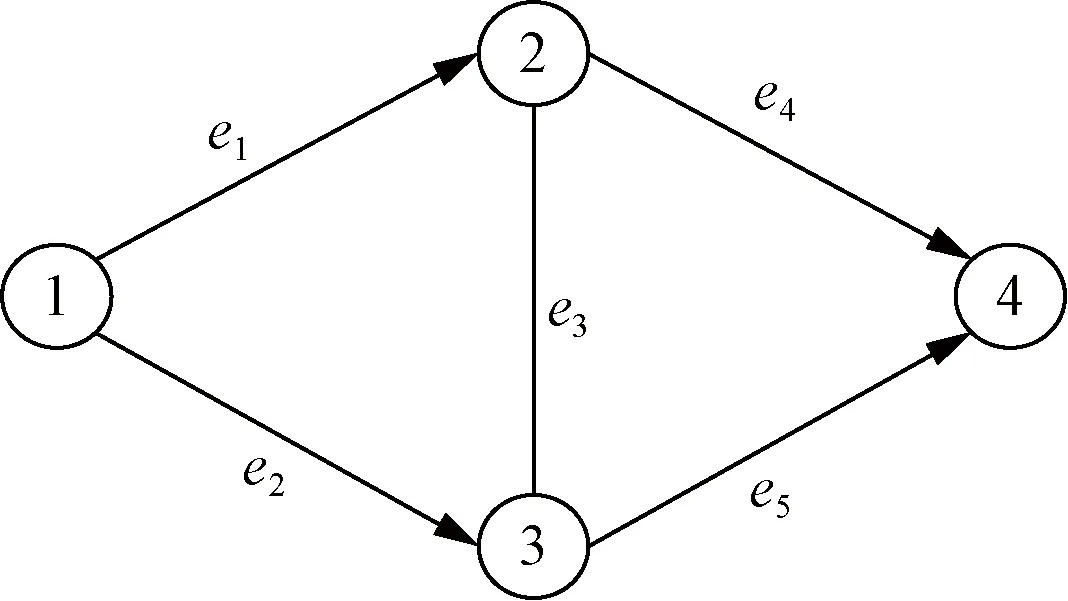
图2 网络流图的一般形式Fig.2 The general form of a network flow graph

V={①,②,③,④};E={(①,②),(①,③),(②,③),(②,④),(③,④)}。

网络流图的一般表示形式如图2所示。

在工程应用中,网络流需对具体物理量进行具体分析。比如,站场中管道为边,设备为节点,管道与设备都在客观上存在一个失效概率,当计算系统的整体失效概率时,就要对节点和边进行赋予特别的权重,即失效概率,从而分析拓扑结构计算网络系统的整体可靠性[9]。确定权重的网络流图G被称为赋权网络流图,其表达式为

G=G(w)={V(w),E(w)}

(3)

式(3)中:V为网络流图G的点集,网络节点为其元素;E为网络G的边集,边为其元素;w为权重,在天然气站场系统可靠性的研究中表示为失效概率。

1.2 最小路集及其求解方法

1.2.1 路集

由有向弧或无向弧组成的任意两个节点之间的弧集称为两个节点之间的路。从输入节点到输出节点的所有路的集合称为路集。则对于图2来说,e1、e2、e3、e4、e5都是路集。显然,当网络流图中的所有弧都正常时,系统正常运行。因此,网络流图中弧的全集合是一个路集。

1.2.2 最小路集

若路中的任何一条弧被删除,它就不再是一条路,可以说这些弧在两个节点之间形成了一条最小路径,这就是最小路[10]。在天然气站场系统可靠性分析中,输入和输出节点之间的最小路尤为重要。如果系统路径通过同一节点或交叉点不超过两次,则两个节点之间的路径将是最小的。最小路的集合称为最小路集,采用布尔行列法来求解最小路集。

设一个站场网络G有m个节点,定义相应的m阶矩阵C=[cij],称C为网络G的关联矩阵。

(4)

布尔行列法,即写出站场网络G的关联矩阵C,给定网络的关联矩阵C,构建一个与关联矩阵C同维数的单位矩阵U与C相加,得到矩阵C+U。此时C+U矩阵维数是m×m,删去矩阵中对应于输出节点的行与对应于输入节点的列元素,形成一个新的矩阵S,将S展开为布尔积的和,根据线性代数理论便可得到网络流最小路集[11]。

网络流可靠性是指网络流在有限的条件内,通过节点集和边集到达指定集的概率,其应用最广泛的计算方法是最小割集法和最小路集法。最小割集法是分析网络故障的常用方法,主要用于分析系统网络流的可靠性。采用最小路集方法对站场网络流进行可靠性分析。由于站场系统网络流较为复杂,为避免分析时出现“维数爆炸”问题,对最小路集做不交化处理。

综上,应用网络流理论进行站场系统可靠性分析的步骤如下。

步骤1明确站场系统工艺流程及拓扑结构划分。

步骤2应用网络流理论对站场系统拓扑结构进行简化,即绘制站场系统网络流图。

步骤3通过分析网络流图,写出网络流图的关联矩阵,并求取系统网络流图的最小路集。

步骤4赋予网络分支权重,权重指的是失效概率,并计算各分支失效概率。

步骤5基于不交化算法简化计算公式,分析站场系统的整体可靠性。

1.3 不交化算法

设一系统网络G,系统网络系统图G{V,E},其中节点数|V|=m,分支数|V|=n。若用Si=(i=1,2,…,W)表示第i条最小路集,用全概率公式表示系统网络系统图G的可靠度RS计算公式为

(5)

展开式(5)共有2W-1求和(或差),路集Si的展开式又是连乘积,因此应用不交化算法对其进行简化。

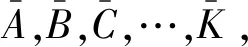
将基本性质扩展可得

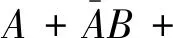
(6)

(7)

依据式(6)和式(7)将系统可靠度的计算公式简化,得到其不交和公式为

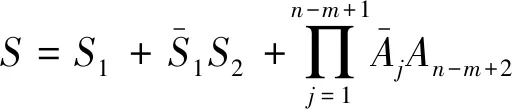
(8)

与式(8)比较发现,项数从2n-m+2降到n-m+2,同式(7)相比,项数从2n-m+2减少到n-m+2,计算公式更加简洁[9]。综合以上理论分析,站场系统的可靠度计算步骤如下。

步骤1求得系统的最小路集Si=(i=1,2,…,W),求得网络流系统的S的不交和表达式为

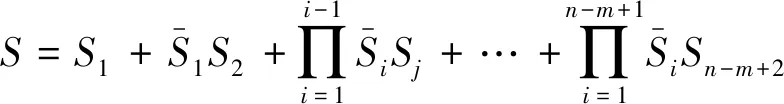
(9)

步骤2不交和表达式中的第i项,对于任意给定的Si,根据命题2求得Si←j,i=0,1,…,i-1。

步骤3利用不交化定理进行化简。

(10)

步骤4求得系统网络流可靠度RS如式(11)所示,其中P(x)为x的可靠度为

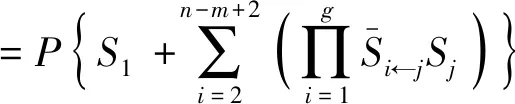
(11)

1.4 基于HAZOP分析的工艺参数偏差状态

当站场系统进行工艺参数调整时,站内设备及管道的失效概率会发生变化,进而影响整个站场系统的可靠性。比如开采后期来液量增大,会使分离器负荷增大,相应地会产生排污系统负荷也增大等影响,导致设备及管道的腐蚀速率在一段时间内增大,从而影响站场设备乃至于整个站场系统的可靠性。通过站场系统的HAZOP分析,识别出风险水平处于“高风险”与“极端风险”风险状态的工艺状态,将其定义为工艺参数偏差状态,如图3所示,并通过假设状态持续时间与腐蚀速率,得到该状态下受影响的设备与管道的剩余壁厚与腐蚀缺陷深度,然后基于ANSYS-PDS模块模拟受影响的设备与管道的失效概率,进而可以分析工艺参数偏差状态与正常运行状态下的站场可靠性之间的联系与偏差。

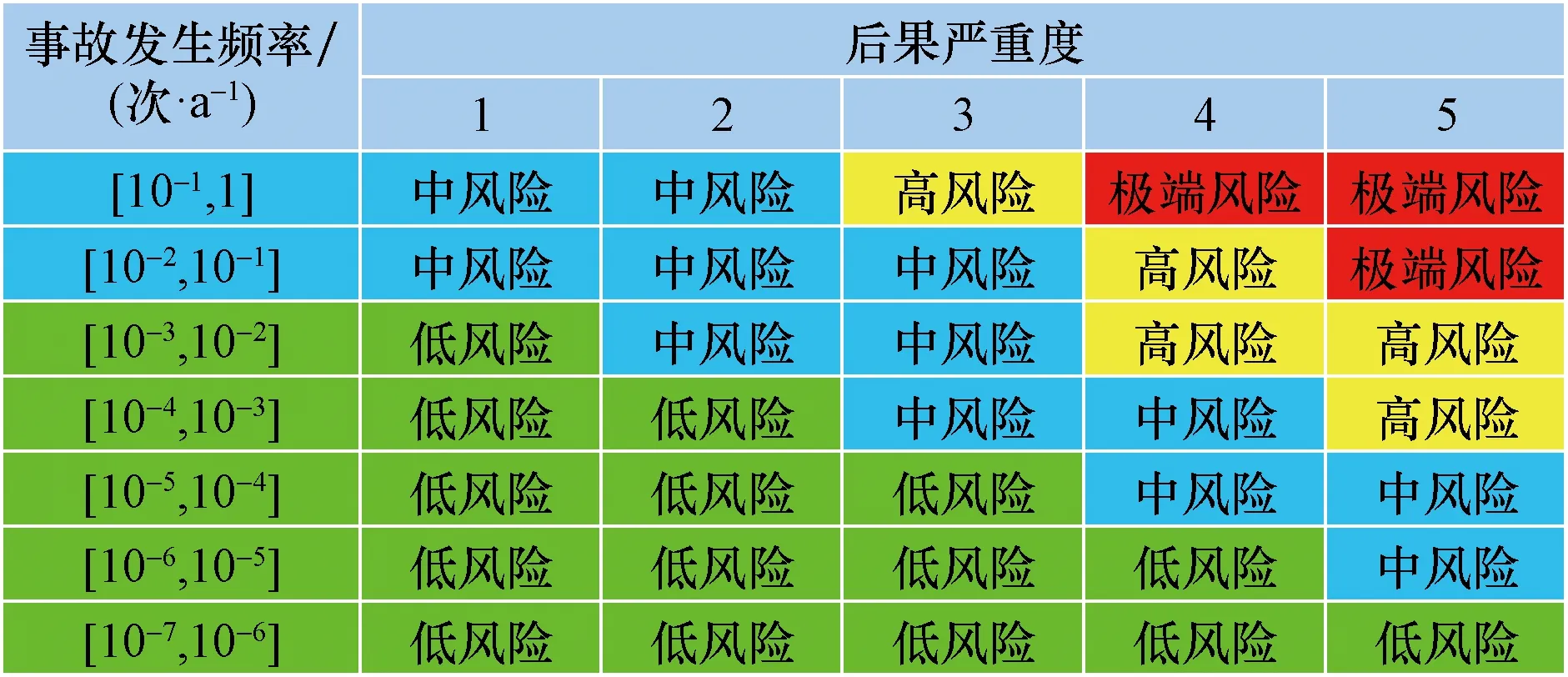
图3 HAZOP分析的风险水平分析图Fig.3 Risk level analysis diagram of HAZOP analysis

2 网络流整体法与分步法的适用性分析

对网络流理论进行调研分类[13-15]可以得出,网络流求解站场系统可靠性时可以分为两类,即整体法与分步法。

整体法即不对站场进行子系统分类,不需分析子系统之间的串并联拓扑结构,而是统一分析整个站场系统,通过计算整个站场系统的最小路集,计算得出站场系统的整体可靠度。此时的最小路集为狭义最小路集,即如果一条路中任意一条弧被除去,就不再是一条通路,则称这些弧构成的路集为最小路集。

分步法即对站场系统进行子系统分类,基于布尔行列法分别计算每个子系统的最小路集,最后根据各个子系统在站场系统中的拓扑结构关系及现场工艺要求分析整个站场系统的最小路集以及计算整体可靠度。此时的最小路集为广义最小路集,即如果一条路中任意一条弧被除去,就不再是一条能满足规定要求的通路,则称这些弧构成的路集为最小路集。

以X站为例,采用两种方法分别计算分析,从而对两种方法进行适用性分析。

2.1 基于网络流整体法的正常工艺状态站场系统可靠性分析

为了分析站场系统可靠性,需要绘制系统的网络流图。网络流图要在符合实际的基础上进行简化,经过简化的系统结构必须能够反映站场系统的结构特点。根据X站工艺流程图,对X站系统网络流图的节点和分支依次编号,从井口采气管线开始顺序进行,直至出站管线,站场系统的实际工艺流程图如图4所示,网络流图如图5所示,网络流图中边与节点的含义如表1所示。X站系统的设备与管道正常工艺状态下失效概率基础数据如表2所示。

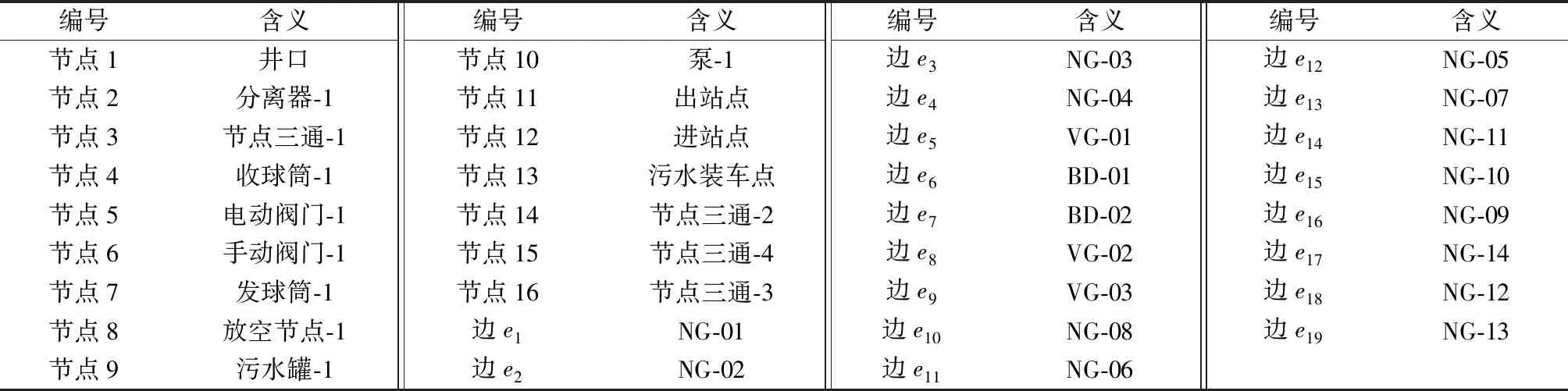
表1 X站系统网络流图节点与边含义Table 1 The meaning of nodes and edges in network flow graph of station X system

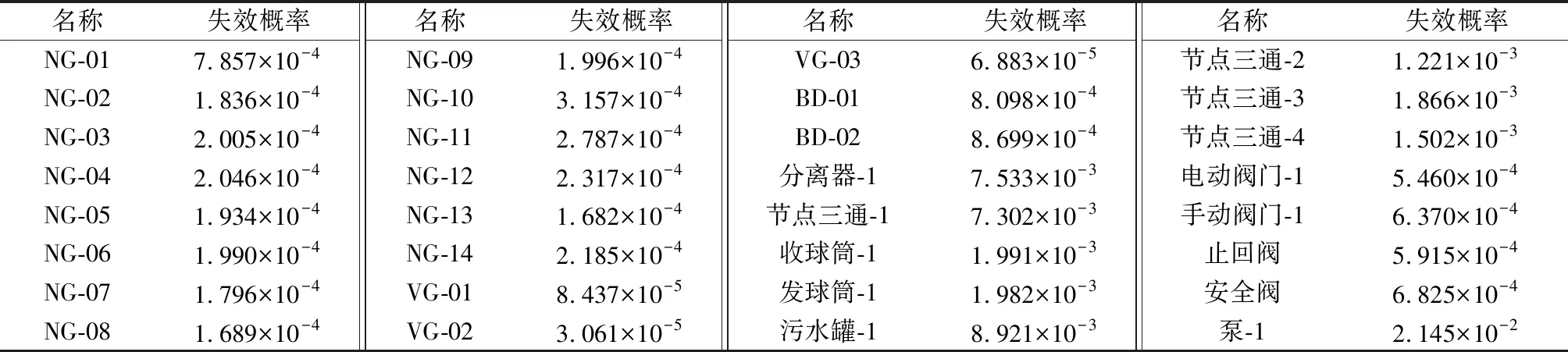
表2 X站系统设备与管道正常工艺状态下的失效概率Table 2 Failure probability of station X system equipment and pipelines under normal process conditions

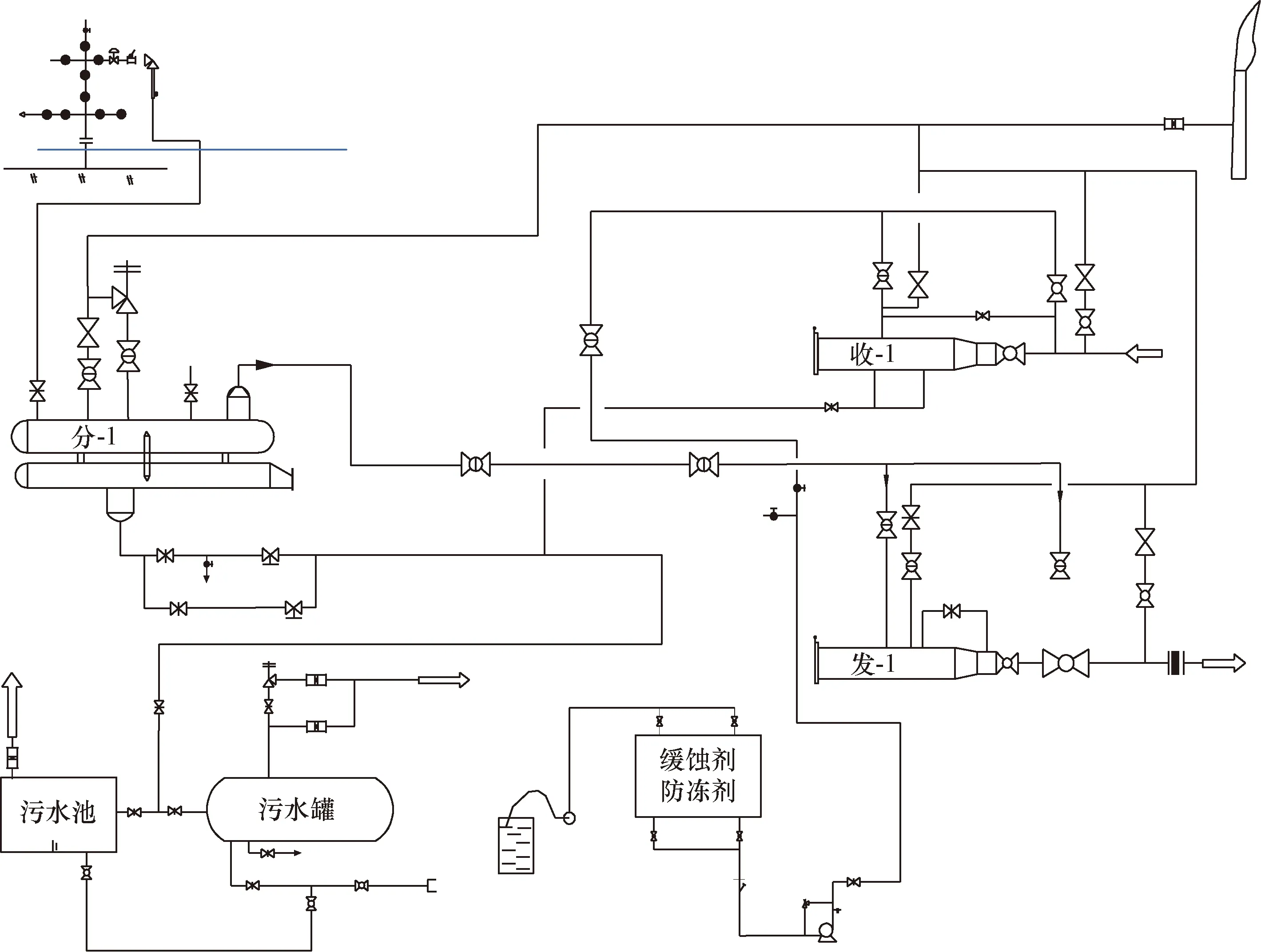
图4 X站的工艺流程图Fig.4 Process flow diagram of station X

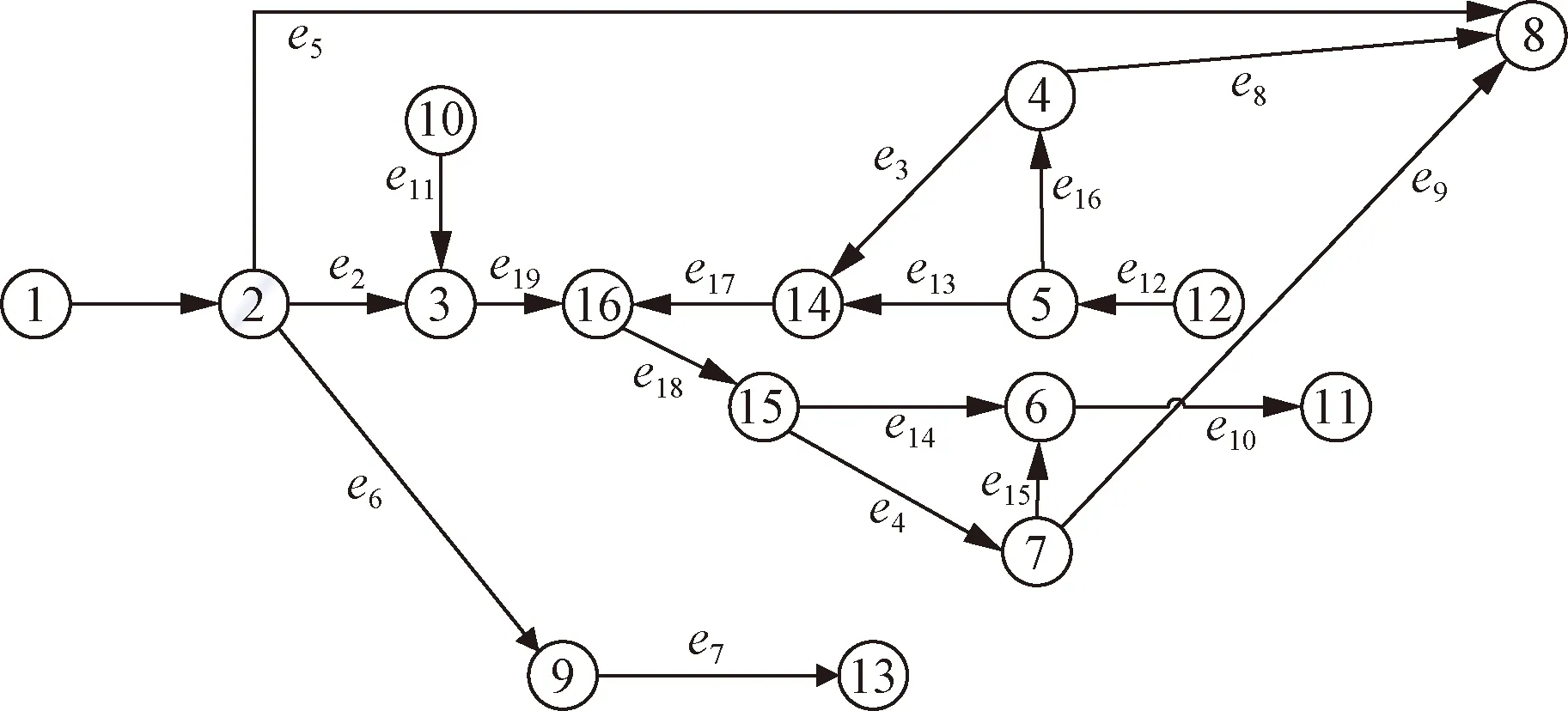
图5 X站的网络流图(整体法)Fig.5 Network flow diagram of station X(holistic approach)

根据X站系统网络流图可以写出该系统的关联矩阵C,构造单位矩阵U,该矩阵为与C同维数的单位矩阵,可得矩阵C+U;去掉矩阵C+U中对应于最终输入节点的行与对应于最初输出节点的列,形成新矩阵S,并构建矩阵S的行列式|S|。

将|S|展开为布尔积的和,采用MATLAB的det程序求解便可得到网络流最小路集如下。

S1={e1,e6,e7,e8,e10,e11,e12,e14,e16,e18,V1,

V2,V3,V4,V5,V6,V8,V9,V10,V11,V12,V13,

V15,V16};

S2={e1,e4,e6,e7,e8,e10,e11,e12,e15,e16,e18,V1,

V2,V3,V4,V5,V6,V7,V8,V9,V10,V11,V12,

V13,V15,V16} 。

对以上最小路集进行不交和运算,并根据式(10),结合网络流图与计算所得设备及管道失效概率,可计算得到整个X站系统可靠度RS为

=Pe1Pe6Pe7Pe8Pe10Pe11Pe12Pe14Pe16Pe18PV1PV2×

PV3PV4PV5PV6PV8PV9PV10PV11PV12PV13PV15×

PV16+(1-Pe14)Pe1Pe4Pe6Pe7Pe8Pe10Pe11×

Pe12Pe15Pe16Pe18PV1PV2PV3PV4PV5PV6PV7PV8PV9×

PV10PV11PV12PV13PV15PV16

=0.942 272 991。

则X站系统的失效概率Pf为。

Pf=1-RS=1-0.948 715=5.129 5×10-2。

2.2 基于网络流分步法的正常工艺状态站场系统可靠性分析

基于分步法原理,根据X站工艺流程图,划分X站的各个子系统,并对X站系统网络流图节点和分支依次编号,从井口采气管线开始顺序进行,直至出站管线,站场系统网络流图如图6所示,节点与边编号含义如表1所示。

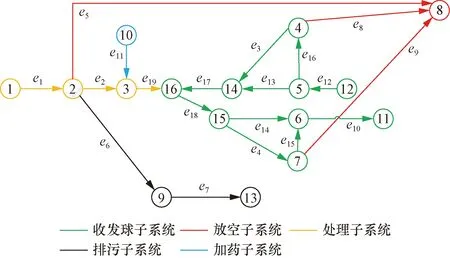
图6 X站系统网络流图(分步法)Fig.6 Network flow diagram of station X (step-by-step method)

根据图6可知,将X站系统分为了5个子系统,即放空子系统、处理子系统、排污子系统、加药子系统与收发球子系统,各子系统之间是串联关系,子系统内部会存在串联或者串并联关系。因此对5个子系统根据工艺要求分别采用布尔行列法计算最小路集,最终按照各子系统串联形式计算整个站场系统的失效概率。

2.2.1 广义最小路集求解

根据图6可知,放空子系统有3条边与1个节点,且3条边均为输入边,处于并联状态,根据狭义最小路集定义可知,放空子系统没有最小路集,但根据现场工艺要求,现场正在投入使用的设备的放空管线必须是正常状态,因此,放空子系统的三条边与1个节点是否在整个系统的最小路集中,应按照其他子系统最小路集中所涉及设备是否有放空路径所判断。

如处理子系统中2节点(分离器)在处理子系统的唯一最小路集中,因此也在系统的每个最小路集中,因此为满足现场工艺要求,放空子系统的边e5及节点8应在系统的每个最小路集中。

同理,边e8、e9涉及收发球子系统,因此收发球子系统的4个最小路集中涉及的放空管线需呈正常状态,收发球子系统最小路集S1中没有涉及带有e8、e9的设备,因此该最小路集中不包括放空子系统的边与节点;收发球子系统最小路集S2中涉及带有e9的设备,即节点7(发球筒-1),因此系统在该最小路集中包括放空子系统的边e9;收发球子系统最小路集S3中涉及带有e8的设备,即节点4(收球筒-1),因此系统在该最小路集中包括放空子系统的边e8;收发球子系统最小路集S4中涉及带有e8、e9的设备,即节点4(收球筒-1)与节点7(发球筒-1),因此系统在该最小路集中包括放空子系统的边e8、e9。

以收发球子系统为例进行分析。根据图7可知,该子系统是整体串联,局部并联的混联系统。写出该系统的网络流关联矩阵C;构造单位矩阵U,可得矩阵C+U;形成新矩阵S,并构建矩阵S的行列式|S|。

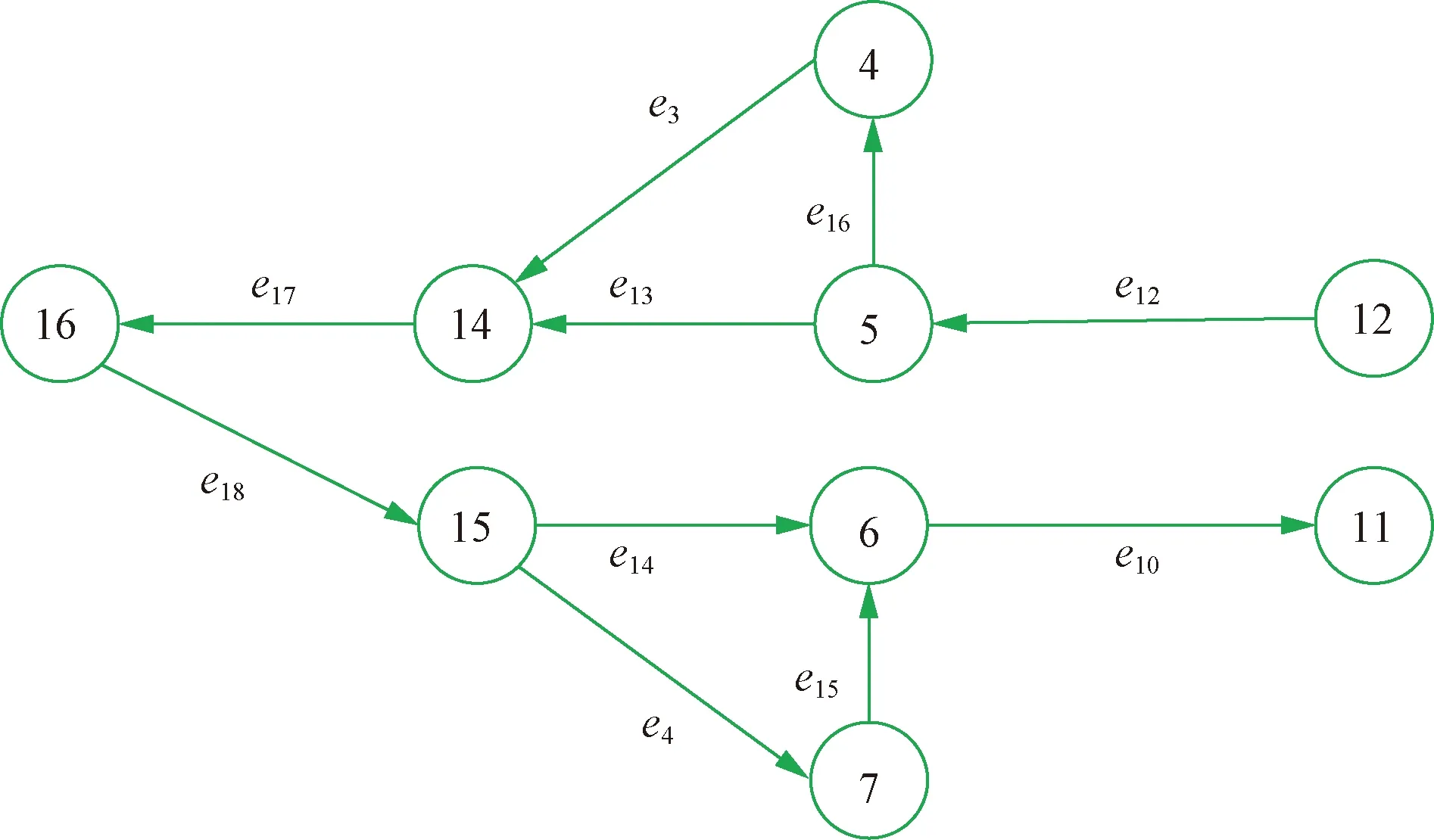
图7 收发球子系统网络流图Fig.7 Network flow diagram of sending and receiving ball subsystem

通过MATLAB的det函数求解,得到收发球子系统网络中的最小路集为S1、S2、S3、S4,分别为

S1={e10,e12,e13,e14,e17,e18,V5,V6,V11,V12,

V14,V15,V16};

S2={e4,e10,e12,e13,e15,e17,e18,V5,V6,V7,V11,

V12,V14,V15,V16} ;

S3={e3,e10,e12,e14,e16,e17,e18,V4,V5,V6,V11,

V12,V14,V15,V16} ;

S4={e3,e4,e10,e12,e15,e16,e17,e18,V4,V5,V6,

V7,V11,V12,V14,V15,V16} 。

2.2.2 系统失效概率求解

由于网络流分步法基于广义的最小路集,在求解放空子系统最小路集时,由于现场工艺要求的限制,最小路集受到其他子系统的约束,因此将放空子系统的边与节点放到其他涉及放空管线的子系统中,进行整体最小路集的求解。

对去掉放空子系统之外的其他4个子系统的最小路集进行不交和运算。

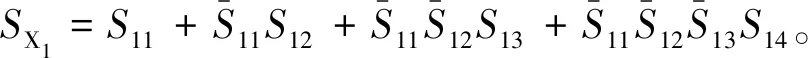
其中,

最小路集S11={e10,e12,e13,e14,e17,e18,V5,V6,V11,V12,V14,V15,V16};

最小路集S12=S2+{e9}={e4,e9,e10,e12,e13,e15,e17,e18,V5,V6,V7,V11,V12,V14,V15,V16} ;

最小路集S13=S3+{e8}={e3,e8,e10,e12,e14,e16,e17,e18,V4,V5,V6,V11,V12,V14,V15,V16} ;

最小路集S14=S4+{e8,e9}={e3,e4,e8,e9,e10,e12,e15,e16,e17,e18,V4,V5,V6,V7,V11,V12,V14,V15,V16} 。

根据式(10),结合网络流图与计算所得设备及管道失效概率,可计算收发球子系统可靠度如下。

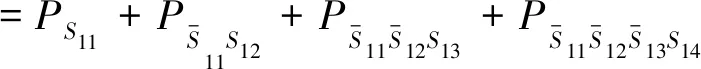
=0.993 254 46。

同理,RSX2=Pe1Pe2Pe5Pe19PV1PV2PV3PV8=0.983 345 001,X2子系统为处理子系统+放空子系统的{e5,V8};RSX3=PS6=Pe6Pe7PV9PV13=0.989 414 984,X3为排污子系统;RSX4=PS7=Pe11PV10=0.978 355 268,X4为加药子系统。

根据现场工艺要求,按照各子系统串联形式计算整个站场系统的可靠度为

则X站系统的失效概率为

Pf=1-RS=1-0.950 131=5.454 36×10-2。

2.3 网络流整体法与分步法适用性对比

根据基于网络流整体法与分步法的站场系统失效概率计算过程,可以对比两种方法对于站场系统可靠性分析的适用性,两者对比如图8所示。

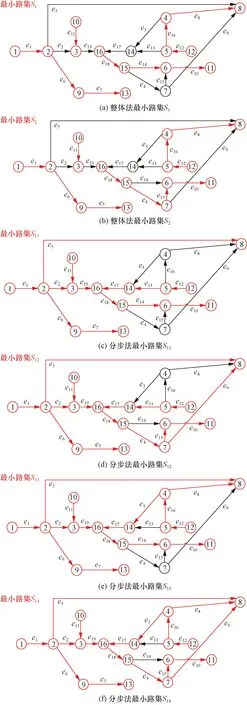
图8 网络流整体法与网络流分步法适用性对比Fig.8 Comparison of applicability between network flow holistic method and network flow step-by-step method

根据表2中站场系统网络流最小路集对比可以发现,整体法最小路集有两个,即S1与S2。S1与S2是站场系统中的最小路,其中去掉任意弧都不能构成完整通路,所包含的节点数与边最大限度内减少,但其存在必要通路不在最小路集内的问题,如e2通路作为天然气处理后的通路应在站场系统的最小路集内,但两条最小路集中均不包含。

分步法最小路集有4个,即S11、S12、S13、S14。分步法最小路集为广义上的最小路集,去掉任意弧站场系统网络流都不能完成相关功能,其所包含的节点与边比整体法要多,但其不存在必要通路不在最小路集内的问题,既能保证连通性又能保证满足工艺要求。整体来看,分步法虽步骤相对复杂,但相对整体法来看更符合现场工艺要求与实际情况,因此选择网络流分步法用于后续系统的可靠性分析。

3 基于HAZOP分析的工艺参数偏差状态下的站场系统可靠性分析

工艺参数偏差状态下的站场可靠性分析,首先要对涉及失效概率会发生改变的设备计算在该状态下的腐蚀缺陷深度,然后对设备重新采用ANSYS-PDS模拟得到新的失效概率,从而基于网络流分步法再次计算站场系统失效概率,进而分析工艺参数偏差状态对站场系统可靠性的影响。

调研X站现场评价的HAZOP分析中偏离分析结果可以得出,X站的工艺参数偏差状态有1个,编号为44207,具体状态为处理子系统来液量过高导致的分离器或污水罐液位过高。此时,站场系统内工艺状态主要会发生改变的设备如表3所示。

表3 工艺状态主要会发生改变的设备与管道Table 3 Equipment and pipelines whose process state will mainly change

根据现场腐蚀监检数据,假设该状态下的设备腐蚀速率为历史最大腐蚀速率,腐蚀时间假设为10 d,对于工艺状态会发生改变的设备进行新的腐蚀速率积分则可得到此时的剩余壁厚,进而通过ANSYS-PDS模拟得到新的失效概率[16],而对于其他设备与管道的失效概率则没有影响。根据该状态下的剩余壁厚再次进行ANSYS-PDS模拟,对于井口来气节点以及污水装车节点,默认为可靠度为1,不再计算。将计算所得工艺参数偏差状态下设备的失效概率与正常状态下的失效概率计算对比,工艺参数偏差状态下设备与管道的失效概率明显增大,如表4所示。

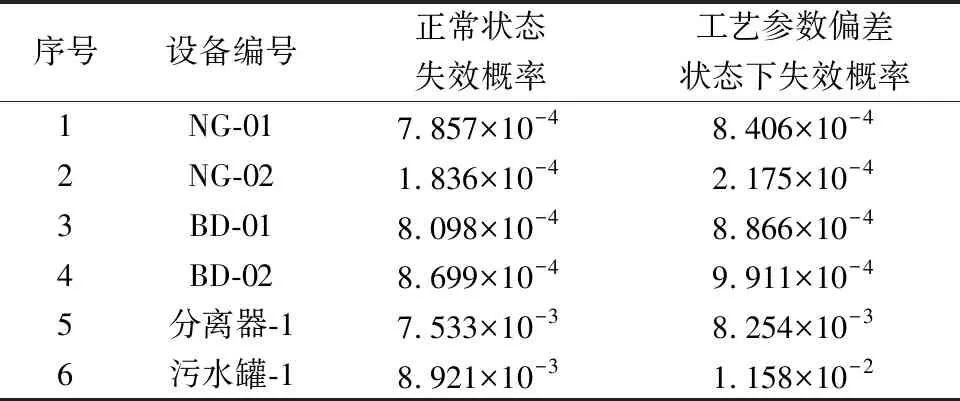
表4 工艺参数偏差状态下设备失效概率计算结果Table 4 Calculation results of equipment failure probability under the condition of process parameter deviation

基于网络流分步法再次计算X站系统失效概率,计算步骤与2.2节相同。此时,站场系统的拓扑结构不发生改变,因此站场系统的广义最小路集不发生改变,只是在系统失效概率计算中各节点与边的失效概率发生改变。

同2.2节相同,将放空子系统的边与节点放到其他涉及放空管线的子系统中,求解整体最小路集。对去掉放空子系统之外的其他4个子系统的最小路集进行不交和运算。同时,工艺参数偏差状态下涉及的4条管道与2个设备属于处理子系统与排污子系统,因此只需要对两个子系统重新进行不交和运算即可。

其中,处理子系统+放空子系统的{e5,V8},RSX2=Pe1Pe2Pe5Pe19PV1PV2PV3PV8=0.982 543 324;排污子系统RSX3=PS6=Pe6Pe7PV9PV13=0.986 564 912。

X站系统的可靠度为

X站系统的失效概率为

Pf=1-RS=1-0.941 964=5.803 6×10-2。

4 结果与讨论

根据X站基于网络流法的正常工艺状态与工艺参数偏差状态的站场可靠性分析,可对X站进行整体可靠性分析与失效概率溯源分析,这对于X站的实际生产运行具有一定的指导参考意义。

(1) 正常工艺状态下X站的站场系统失效概率为4.986 9×10-2,将放空子系统分散于其他子系统中,计算可得各子系统的失效概率分别为:收发球子系统+放空子系统的{e8,e9}失效概率为6.745 5×10-3,处理子系统+放空子系统的{e5,V8}失效概率为1.665 5×10-2,排污子系统失效概率为1.058 5×10-2,加药子系统失效概率为2.164 5×10-2,由此可知,除收发球子系统失效概率为10-3数量级外,其余子系统失效概率均为10-2数量级,且加药子系统失效概率最大,因此X站系统在正常工艺状态下建议重点关注各子系统的排序为:加药子系统>处理子系统+放空子系统的{e5,V8}>排污子系统>收发球子系统+放空子系统的{e8,e9}。

(2) 工艺参数偏差状态下X站的站场系统失效概率为5.803 6×10-2,较正常工艺状态增大16.38%,经计算可得各子系统的失效概率分别为:收发球子系统+放空子系统的{e8,e9}失效概率没变,处理子系统+放空子系统的{e5,V8}失效概率为1.745 7×10-2,较正常工艺状态增大4.82%,此时站场应及时关注;排污子系统失效概率为1.343 5×10-2,较正常工艺状态增大26.92%,此时站场应重点关注;加药子系统失效概率没变,因此X站该工艺参数偏差状态对于排污子系统影响最大,其次是处理子系统。各子系统的失效概率数量级没有改变,大小排序也没有改变,因此工艺参数偏差状态下建议重点关注各子系统排序不变。

(3) X站在正常工艺状态与工艺参数偏差状态下的子系统失效概率大小排序相同,即加药子系统>处理子系统+放空子系统的{e5,V8}>排污子系统>收发球子系统+放空子系统的{e8,e9},回溯其可靠性分析过程可得出具体原因如下。

原因1加药子系统失效概率包含一台泵设备,而采用泵设备的失效概率为2.145×10-2,与压力容器与管道的失效概率相比较大,因此该子系统的失效概率不可避免地偏大。

原因2处理子系统+放空子系统的{e5,V8}设备与管道均处于正在处理的状态,此时腐蚀环境较为不利,因此各设备与管道的失效概率偏大,子系统的失效概率更大。

原因3排污子系统的失效概率数量级比收发球子系统的失效概率数量级大10倍,这是由于排污子系统长期处于较恶劣的腐蚀环境中,其中的设备与管道腐蚀缺陷较深,失效概率更大,因此在站场日常运行生产过程中,应重点关注排污子系统的腐蚀状况,将其控制在合理安全的范围之内;而收发球子系统涉及的设备与管道失效概率均为较低水平,因此该子系统失效概率最小。

5 结论

(1) 提出采用跨领域的网络流理论来分析天然气站场系统的整体可靠性,并对网络流理论做了归纳创新,提出了网络流分步法与网络流整体法的概念,方法可直接分析系统整体,比传统图论方法更简洁、更直观。其中,网络流分步法比网络流整体法分析站场系统的可靠性适应性更强,网络流分步法不存在必要通路不在最小路集内的问题,既能保证连通性又能保证满足工艺要求,对于天然气站场的可靠性分析较为适应。

(2) 通过最小路集与不交化算法计算出站场系统在正常工艺状态下的失效概率,正常工艺状态下X站系统失效概率为4.986 9×10-2,经溯源分析,X站系统在正常工艺状态下建议重点关注各子系统的排序为:加药子系统>处理子系统+放空子系统的{e5,V8}>排污子系统>收发球子系统+放空子系统的{e8,e9}。

(3) 创新性地提出基于HAZOP分析确定站场系统在工艺参数偏差状态下的失效概率,分析偏差状态对于站场系统可靠性的影响。工艺参数偏差状态下该站的站场系统失效概率为5.803 6×10-2,较正常工艺状态增大16.38%,两种状态下各子系统的失效概率数量级没有改变,大小排序也没有改变,因此工艺参数偏差状态下建议重点关注的各子系统排序不变,由于此时排污子系统失效概率较大,应重点关注排污子系统的腐蚀状况,将其控制在合理安全的范围之内,对于其他子系统中的设备进行重点关注的调整。这对实现天然气站场整体系统的安全运行管理具有重要意义,为其他类似站场的可靠性分析提供参考和借鉴。