循环荷载下黄土地区桩基础抗拔承载力计算

刘义, 郭家, 韩猛,3, 李哲*, 刘路路,4

(1.陕西省建筑科学研究院有限公司, 西安 710082; 2. 长安大学公路学院, 西安 710064;3. 大连理工大学海岸与近海工程国家重点实验室, 大连 116024;4. 中国矿业大学深部岩土力学与地下工程国家重点实验室, 徐州 221116)

随着基础工程领域的快速发展,抗拔桩的应用场景越来越多,比如在地下室抗浮、高耸建筑物抗拔等情形下,对桩基础都有着较高的抗拔要求[1-3]。随着工程需求的增长,对抗拔桩的要求已经不仅仅局限于在单一拉拔荷载下的抗拔能力,在循环荷载下的抗拔能力也逐渐得到了人们的重视,地下水位变化、海平面升降等情形中都会对抗拔桩施加竖向循环荷载作用。但是在实际中,人们对抗拔桩工作机理的研究相对较少,循环荷载下的承载能力计算方法也一直是工程设计的重难点。因此,正确理解抗拔桩的承载特性,提出合理、简便的极限承载力计算方法,对基础的抗拔设计具有重要的应用价值[4-6]。

前人在抗拔桩的承载特性、循环荷载的作用特点以及抗拔承载力计算方法等方面做了大量的研究。在抗拔桩的承载特性方面,Kyle[7]推导了钻孔桩上拔时侧摩阻力的计算方法,与实测值对比后发现在砂土地基中的吻合度较好。邹积山等[8]研究了抗拔桩在海洋环境中的变化规律,得到了桩基抗拔承载力与孔压的关系。朱碧堂等[9]基于Winkler地基模型推导了抗拔桩极限承载力计算方法,发现抗拔桩的承载能力主要受桩的侧摩阻参数和上覆土层厚度的影响。陈小强等[10]、张忠苗等[11]发现抗拔桩的变形速率远大于抗压桩,认为抗拔设计时应考虑桩顶上拔量、侧摩阻力折减系数。张乾青等[12]在前人研究的基础上,提出了一种可反映单桩在抗拔过程中侧摩阻力发挥程度的计算模型,发现抗拔桩的极限侧摩阻力约为同等条件下抗压桩的0.7倍。在循环荷载研究方面,朱斌等[13]研究了竖向循环拔压荷载下抗拔桩的承载力变化规律,发现荷载循环次数、端阻大小对桩基承载力影响显著。Boulon等[14]通过试验总结得出桩基在循环拉拔作用下承载力的衰减速率约为单向拉拔的3倍。Masatoshi等[15]在考虑衰减速率的同时,发现相对于单向拉拔,抗拔桩在循环拔压下的承载能力降低了约60%。在抗拔桩承载能力计算模型方面,王钦科等[16]、黄茂松等[17]基于抗拔桩的现场破坏性试验,借助3种预测模型对桩基础的荷载-位移(Q-s)曲线进行定量分析,采用多种方法确定了抗拔桩的承载能力。何思明[18]结合国内外众多抗拔桩测试资料,借助桩周土的破裂方程,建立了桩的抗拔承载力模型。许宏发[19]从桩的抗拔机理出发,推导了桩的抗拔承载力理论公式,在抗拔桩的荷载传递方面提出了创新性的非线性计算模型。邹丹等[20]推导了不同密实度的土侧压力系数,考虑粗糙度和桩侧摩阻力的发挥深度,建立了砂土中单桩抗拔极限承载力计算模型。总体来说,国内外研究者们付出了大量的努力,但是仍存在一些不足:一方面,现有研究中多采用模型试验的方法,与现场的差别较大,抗拔桩的承载能力多是借助单一的试验结果或理论推导进行预测,缺乏对试验结果背后规律的总结,难以反映出抗拔桩在实际中的承载情况;另一方面,在循环荷载下桩基础抗拔承载能力计算模型中,抗拔系数的取值多沿用了单一抗拔时的取值方法,忽略了循环作用的影响。

鉴于此,现借助现场试验研究西安一处黄土地基中单桩在循环拉拔和循环拔压荷载下的承载能力,分析循环位移比的变化规律,结合试验数据,修正循环荷载作用下抗拔系数取值方法,提出循环荷载作用下抗拔桩承载能力计算模型。进一步了解抗拔桩在黄土地基中的承载特性,为循环作用下抗拔桩的设计提供一定的参考。

1 现场试验概况

1.1 场地概况

试验场地位于西安市火车站北侧拾翠路中段,占地面积约100 m2,主要地形为洪积二级台地。地表下8 m深度范围内的土层主要由人工填土和黄土组成,具有成层分布的特点,场地地面标高为401.4 m,地下水位在地面以下4.3 m。场地土层物理力学参数如表1所示,桩长范围内土层分布如图1所示。

图1 地质剖面图Fig.1 Geological profile

表1 试验场地土工参数Table 1 Geotechnical parameters of test site

1.2 试验桩设计

试验桩均为钻孔灌注桩,首先清除现场杂物,确定桩位并做好标记,平整场地,安装成孔设备。由于场地空间有限,试验采用落锤式打桩机打孔,同时不断抽取地下水以保证成桩质量;成孔后下放提前制作好的钢筋笼,钢筋笼由人工绑扎而成,主筋采用8φ25钢筋,箍筋采用φ8@150钢筋;紧接着浇筑混凝土,混凝土强度为C25,养护28 d之后再开展试验。

试验桩的布置情况如图2所示。试验桩共有6根,编号分别为1～6,桩径均为600 mm。1号桩长7.0 m,2号桩长6.0 m,分别用于竖向抗压静载试验和竖向抗拔静载试验,3～6号桩长均为7.0 m,其中3号、4号桩用于竖向循环拉拔试验,5号、6号桩用于竖向循环拔压试验。桩间距设置为2.4 m,为4倍桩径。

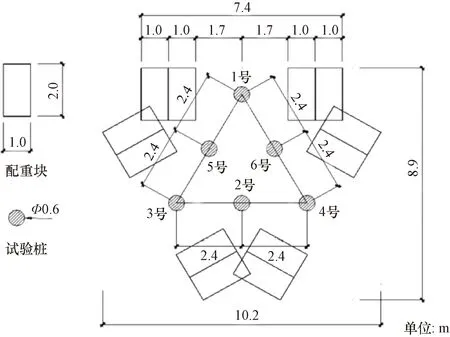
图2 试验桩现场布置Fig.2 Site layout of test piles

4号桩和6号桩为挤密桩,挤密布置情况如图3所示,在距离桩边缘外10 cm和25 cm处各打入1圈钢管,其中第一圈共11根,第二圈共13根,钢管的直径为5 cm,高2 m。

1.3 测试内容

现场试验测试内容主要为桩顶竖向位移和桩身轴力。表2为测试仪器的具体指标,图4展示了现场的测试设备布置,从图4(a)可知,采用指针式百分表测量桩顶位移,最大误差为0.06% FS,分辨率为0.01 mm,根据《建筑桩基检测技术规范》(JGJ 106—2014),在桩身两个方向对称安装4个百分表,在每级荷载施加后的第5、15、30、45、60 min测读桩顶沉降,以后每隔30 min测读一次,直至读数稳定或桩基破坏,破坏标准为当某级荷载下桩顶位移量为上一级的5倍及以上或桩顶累计上拔量超过100 mm。从图4(b)可知,采用振弦式钢筋应力计测量桩身轴力,除2号桩,其余试验桩均布置纵向间距为1 m的6个断面,每个断面设置2个应力计,分别布置在两根主筋上,将应力计导线保护后沿主筋引至桩顶,与读数仪相连接,读取应力计数据;2号桩布置5个断面,应力计布置形式与其他试验桩相同。

1.4 加载过程

现场试验采用慢速维持荷载法加载,按照《建筑桩基检测技术规范》(JGJ 106—2014)进行。加载装置如图5所示,抗压过程中启动下部千斤顶,借助下部钢梁提供反力;抗拔时启动上部千斤顶,以上部钢梁为支撑,借助锚拔板提供反力。

图5 加载装置设计Fig.5 Design of loading device

加载步骤如图6和图7所示,根据《建筑桩基检测技术规范》(JGJ 106—2014),分级荷载为预估极限承载力的0.1倍,因此循环拉拔试验中共设置3个加载循环,各循环的最大荷载依次为150、250和350 kN,每个加载循环中包含3～4个加载级别,分级拉拔荷载均为50 kN。循环拔压试验中共设置5个加载循环,其中抗压环节为2个加载级别,分级荷载为100 kN;抗拔环节为3～4个加载级别,分级荷载为50 kN。

图6 3号、4号试验桩加载步骤Fig.6 loading steps of No.3 and No.4 test pile

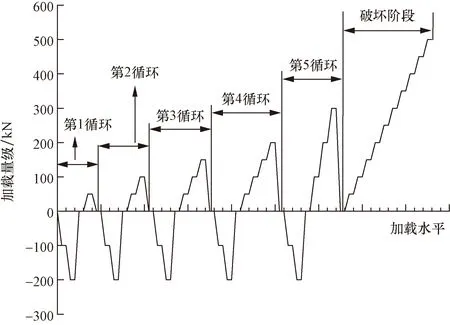
图7 5号、6号试验桩加载步骤Fig.7 loading steps of No.5 and No.6 test pile

考虑不同数量的加载级别一方面是为了能够更加透彻的分析桩基础在循环荷载下的承载机理,另一方面则是防止桩基础在试验初期出现破坏而影响后续试验。

2 模型构建

2.1 基本思想

桩基础抗拔承载力计算模型的创建思路为:①分析循环荷载下循环位移比与循环次数的联系;②总结循环位移比和循环次数、循环荷载比的关系;③归纳循环位移比和循环荷载下抗拔系数的关系;④建立循环荷载下桩基抗拔承载力计算模型。

为了探讨桩顶位移和桩基承载能力的关系,引入了循环位移比,定义循环位移比为某级荷载下桩顶轴向位移量和极限状态下桩顶轴向位移量的比值,表达式见式(1)。图8展示了3～6号桩的循环位移比与循环次数的拟合关系,可以看出,在循环拉拔和循环拔压作用下,循环位移比随着循环次数的增加均近似呈线性增大,且循环位移比的平均增长率分别为0.133和0.08,说明循环拉拔荷载对桩基的安全威胁更大,该结论也验证了郭鹏飞等[21]总结的规律。

图8 循环位移比和循环次数的关系Fig.8 Relationship between cyclic displacement ratio and number of cycles

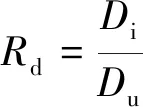
(1)

式(1)中:Rd为循环位移比,根据荷载情况,Rd可分为循环拉拔位移比Rdm和循环拔压位移比Rdk;Di为某级荷载下桩顶轴向位移量,mm;Du为极限荷载下桩顶轴向位移量,mm。

根据《建筑桩基技术规范》(JGJ 94—2008),桩基础在连续拉拔作用下的极限承载力的计算公式为

Tu=∑λiqsikuili+W

(2)

式(2)中:Tu为基桩抗拔极限承载力标准值,kN;ui为破坏表面周长,m;qsik为第i层土的桩侧抗拔极限摩阻力标准值,kPa;λi为抗拔系数;W为桩身自重,kN;k为土层数。

由式(2)可以看出,抗拔系数对计算结果影响显著。相比于连续荷载,循环荷载对桩基础更为不利,在循环荷载下,侧摩阻力强度标准值损失严重[22],循环荷载施加的同时也伴随着桩基侧摩阻力的衰减,此时抗拔系数不仅需要修正拉拔过程中的承载力损失,还要考虑因循环作用造成的侧摩阻力衰减。因此,循环荷载下抗拔系数的取值方法成为了桩基础承载能力是否准确的关键。

为了更好地分析桩基在循环荷载下的试验结果,引入循环拉拔荷载比α、循环拔压荷载比β和循环荷载下的抗拔系数λi,各参数的定义如下。

(3)

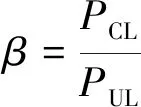
(4)

(5)

式中:α为循环拉拔荷载比;β为循环拔压荷载比;λi为循环荷载下的抗拔系数;Pi为循环拉拔条件下当前拉拔荷载,kN;Pcu为静载情况下极限荷载值,kN;PCL为循环拔压条件下,当前加载级别下最大上拔荷载,kN;PUL为循环拔压条件下,当前加载级别下最大下压荷载,kN;Piu为循环加载后除去桩身自重的桩基抗拔承载力极限值,kN;Pu为除去桩身自重的桩基常规抗拔承载力极限值,kN。

由图8可知,循环位移比和循环次数近似呈线性关系。实际上,桩顶位移和竖向荷载同样有着较大的关联,如周志军等[23]发现桩顶沉降和桩基极限承载力呈正向关系。因此可以认为Rdm、Rdk能够分别满足式(6)和式(7)。

Rdm=M(α,n)

(6)

Rdk=K(β,n)

(7)

循环荷载下的抗拔系数可表示为

λi=V(Rdm,Rdk)

(8)

联立式(2)和式(8),得出循环荷载下桩基抗拔承载力表达式为

Tu=∑V(Rdm,Rdk)qsikuili+W

(9)

2.2 循环拉拔位移比的计算

试验桩在不同循环次数下的循环拉拔荷载比与循环拔压位移比关系如图9所示。由图9可以看出,循环拉拔位移比随着循环拉拔荷载比的增大均逐渐增加,且两者近似满足二次多项式的关系。当循环次数为1次时,循环拉拔位移比的增长速率随循环拉拔荷载比的增加逐渐减慢,随着循环次数的增加,循环位移比的增长速率逐渐加快,且循环次数为2次时近似为增长速率的临界点。这一方面是因为循环荷载逐渐增大,不断接近极限承载力;另一方面则是随着循环次数的增加,桩周土由于反复剪切而屈服[24]。

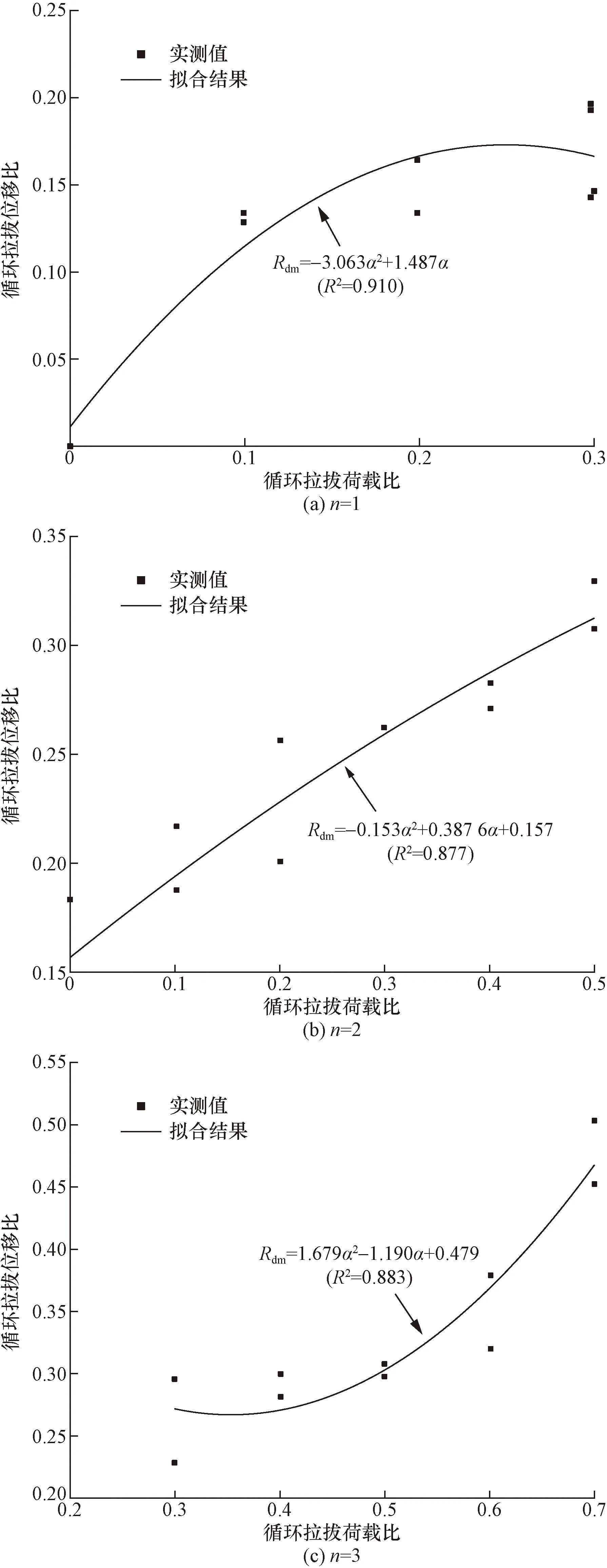
图9 循环拉拔荷载比与循环拉拔位移比的关系Fig.9 Relationship between cyclic drawing load ratio and cyclic drawing displacement ratio

通过对以上各参量的拟合回归,判断循环拉拔位移比与循环拉拔荷载比呈二次多项式关系,拟合程度较好,且循环拉拔位移比与循环次数联系紧密,因此建立循环拉拔位移比的二次模型为

Rdm=A(n)α2+B(n)+C(n)

(10)

式(10)中:A(n)、B(n)、C(n)为关于循环次数n的影响参数,将循环次数和A(n)、B(n)、C(n)的数量关系提取至表3,回归拟合过程如图10所示。

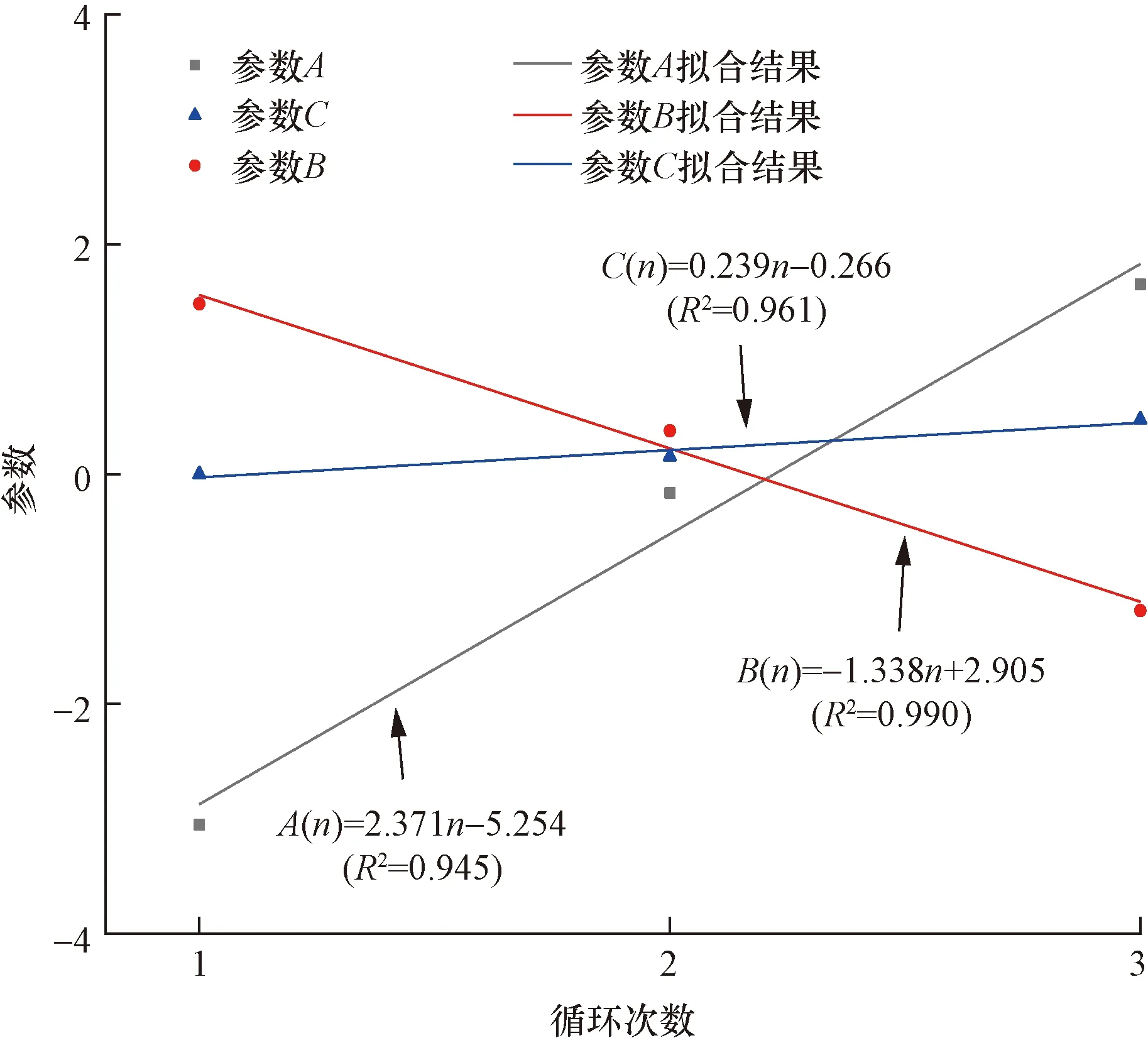
图10 参数A、B、C的拟合Fig.10 Fitting of parameters A, B and C

表3 循环拉拔位移比模型的系数Table 3 Coefficient of cyclic drawing displacement ratio model

根据以上结果,结合式(10),得到Rdm的计算模型为

Rdm=(2.371n-5.254)α2+(-1.338n+2.905)×

α+0.239n-0.266

(11)

式(11)中:0<α≤1;n≤3。

试验桩循环拔压位移比(Rdk)、循环拔压荷载比(β)、循环次数(n)三者之间的关系如图11所示,拟合结果如表4所示。可以看出,当β为1∶4时,Rdk随着n的增加变化较小;当β大于1∶4时,Rdk随着n的增加逐渐增大,且Rdk的增长速率与β和n均呈正向关系,这说明当循环荷载远小于桩基承载能力时,可以忽略循环作用对桩基承载能力的削弱。另外,在同一循环次数下,β的影响程度存在临界值,当β大于5∶4时,Rdk最大为0.50,变化较大,且Rdk的增长速率随n的增大迅速增大,此时循环作用对桩基的承载能力有着巨大的威胁。

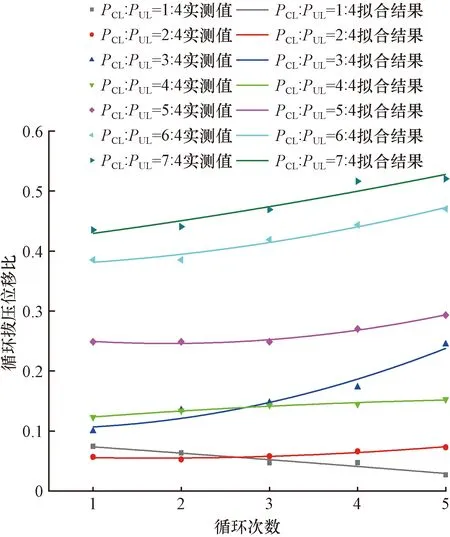
图11 循环次数与循环拔压位移比的关系Fig.11 Relationship between cycle number and cyclic tension-compression displacement ratio

表4 拟合结果Table 4 Fitting results

通过以上分析知循环位移比与循环次数近似满足二次多项式的关系,且受循环拔压荷载比的影响显著,因此建立循环拔压位移比的二次模型为

Rdk=F(β)n2+G(β)n+T(β)

(12)

式(12)中:F(β)、G(β)、T(β)为与循环拔压荷载比相关的参数,将上述计算模型的系数提取,汇总至表5,回归拟合过程如图12所示。

图12 循环拔压荷载比与参数F、G、T关系Fig.12 Fitting of parameters F, G and T

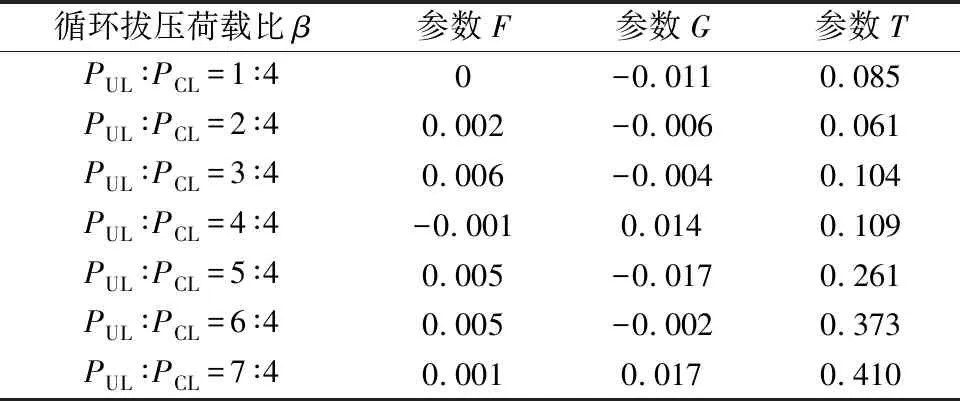
表5 循环拔压位移比模型的系数Table 5 Coefficient of cyclic pull-compression displacement ratio model

结合式(12),循环拔压位移比的计算模型为

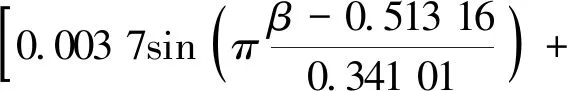
0.18β2-0.109β+0.084

(13)

式(13)中:β为循环拔压荷载比,0<β≤1.75;n为循环次数,n≤5。

2.3 桩基础抗拔模型的建立

图13展示了循环作用下抗拔系数和循环位移比的拟合关系。由图13可知,循环荷载下的抗拔系数随循环位移比的增大逐渐减小,当循环位移比为0.844时,循环荷载下的抗拔系数为0.545,桩基承载能力的衰减率接近50%,可见循环作用对桩基础

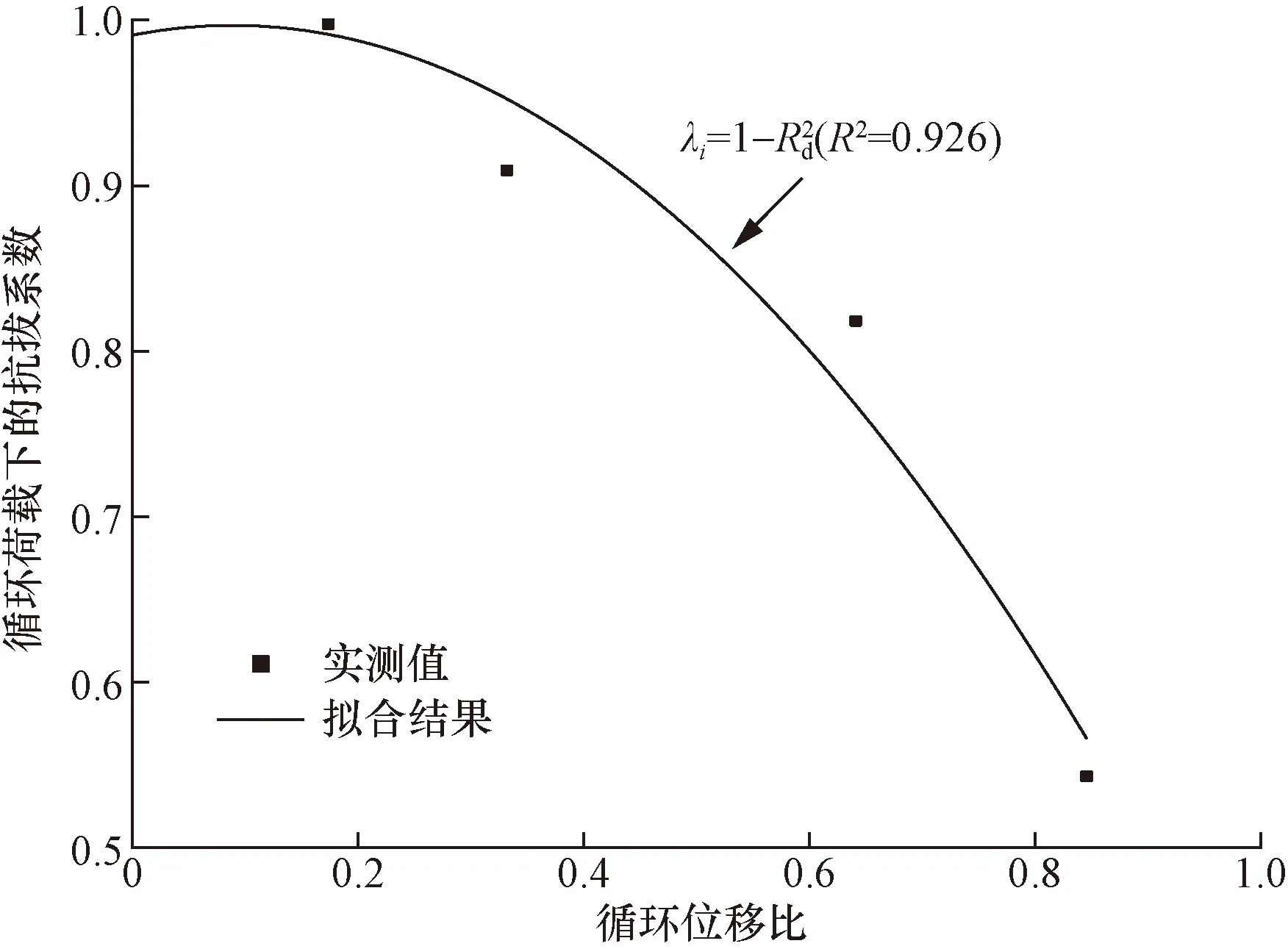
图13 Rd与λi的关系Fig.13 Relationship between Rd and λi

具有较大的影响。另外,循环荷载下的抗拔系数衰减速度随着循环位移比的增大而加快,一方面是因为循环作用反复剪切桩周土使其屈服,另一方面是因为循环位移比越大,桩周土的扰动越严重,侧摩阻力被削弱使抗拔系数快速衰减,这说明桩基础承载能力会随着循环位移比的增大加速衰减,循环位移比在承载力衰减方面具有“放大效应”,这与Mcmanus等[25]的相关结论是一致的。因此在设计中应重视循环位移比的作用,合理控制其“放大效应”。

综上,得到循环荷载作用下桩基础抗拔承载力计算模型如下。

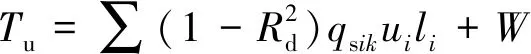
(14)

(15)

式中:Tu为桩的极限抗拔承载力,kN;ui为桩身截面周长,m;qsik为桩周第i层土的单位面积极限侧阻力标准值,无当地经验时,可根据规范中给定的参考值选取,kPa;li为第i层土的层厚,m;W为桩自重,水下部分的桩自重按浮重力计算,kN。

由图13知,Rd≤1,因此当n=3且Rdm=1时,求得α=0.918,所以为了保证模型的准确性,需保证0<α≤0.91,n≤3。

3 模型验证

为验证所提极限承载力计算模型的合理性和准确性,基于现场试验对现场试验结果、常规计算结果和本文模型的计算结果进行比较分析。

3.1 实例1

以试验中3号和5号桩为例,对规范计算结果、本文模型计算结果和实测结果进行比较,试验情况见上述介绍。经计算,3号桩和5号桩的循环位移分别为0.58和0.47,循环作用下的抗拔系数分别为0.65和0.78。根据《建筑桩基技术规范》(JGJ 94—2008),取地下水位以上和以下的侧阻力标准值分别为58 kPa和46 kPa,桩身自重均为50.32 kN,计算得到3号桩和5号桩的承载力分别为513 kN和569 kN。而按照《建筑桩基技术规范》(JGJ 94—2008)中抗拔桩的承载力计算方法,得到抗拔桩的极限承载力为578 kN。

经过上述计算,得出三者的对比结果如图14所示。在循环拉拔荷载下,本文模型计算值略大于实测值,误差率为2.6%,规范法误差率为15.6%;在循环拔压荷载下,本文计算模型值略大于实测值,误差率为3.5%,规范法误差率为4.5%。

图14 承载力计算结果对比Fig.14 Comparison of bearing capacity calculation results

3.2 实例2

取文献[24]中1根试桩的试验结果验证本文模型的可靠性。试验场地位于杭州萧山,场地由上向下土层依次为杂填土、黏质粉土、砂质粉土、卵石,持力层平均液性指数为0.71。试桩为钻孔灌注桩(S1),桩径0.8 m,桩长37.11 m,桩身混凝土等级为C35,桩身自重约446 kN,桩端打入持力层深度2 m。加载方法根据《建筑桩基检测技术规范》(JGJ 106—2014),采用支墩-反力架装置,利用千斤顶反力分级加载。每根试桩均设置3个加载循环,每个循环的最大值均为4 000 kN,加载过程中分级荷载设置为400 kN,卸载过程中分级荷载设置为800 kN。

图15展示了本文模型计算结果、规范计算结果和实测值的对比。由图15可知,本文模型计算值略大于实测值,误差率为3.3%,规范法误差率为75.7%,同时印证了2.4节中提出的循环荷载下桩基承载力衰减规律。

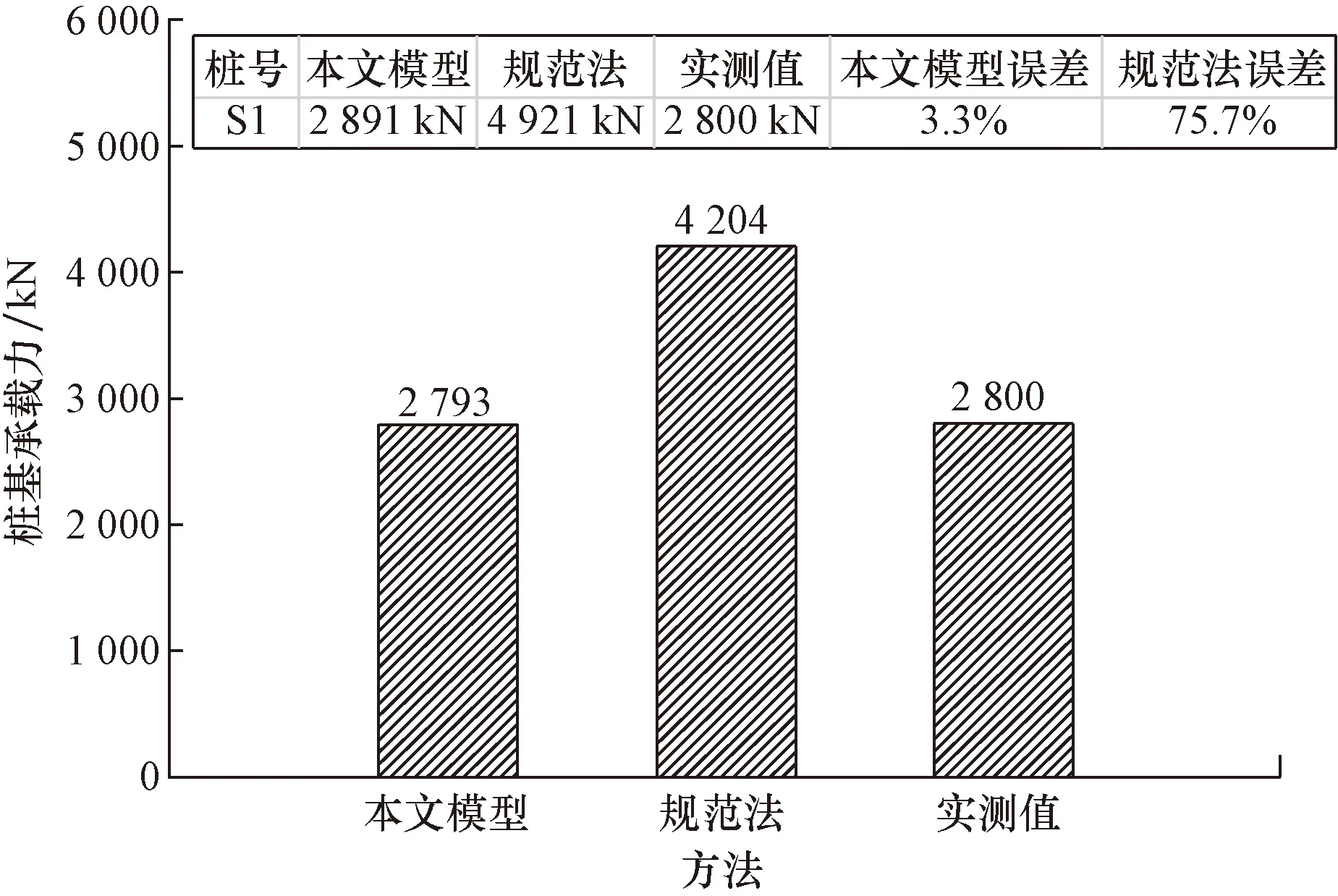
图15 S1试桩计算结果对比Fig.15 Comparison of calculation results of S1 test pile

通过验证,可以看出提出的循环荷载下抗拔桩的承载能力计算模型是可靠、合理的,能够比较准确地预测抗拔桩的承载能力,该计算方法简单、准确,便于现场快速的计算和分析,在工程中应用前景广阔。

4 结论

基于现场试验建立了循环荷载下黄土地区桩基础抗拔承载力计算模型,得出以下结论。

(1)基于现场试验,得出了循环荷载下桩基承载力的变形机理。桩基础在循环荷载和单一荷载作用下的承载能力差异较大,在循环荷载下的承载能力受循环荷载比和循环次数的影响显著,在循环拉拔荷载作用下,当循环次数超过2次时,桩基承载力衰减较快;在循环拔压荷载作用下,当循环拔压荷载比大于5∶4时,循环次数对桩基承载力的影响显著。

(2)基于现场试验结果,推导了循环位移比与循环荷载比和循环次数的关系,拟合了循环作用下抗拔系数与循环位移比的回归方程,建立了桩基础抗拔承载力计算模型。提出的模型综合考虑了循环位移比、循环荷载比和循环次数的影响,优化了传统计算模型中忽略循环作用的缺陷。

(3)通过工程案例研究发现,传统的计算模型高估了循环作用下抗拔桩的承载能力,与实测值相差15%以上。而本文模型进一步考虑了循环荷载对桩基承载力的削弱,与实测结果的误差均控制在4%以内,体现出了本文模型的准确性与合理性。在计算循环荷载下抗拔桩的承载能力时,建议采用本文模型。