基于经验耦合函数的动态运行参数异常检测

宋柯, 钱唐江, 武彬, 陈勇旭, 钟婷, 周帆*

(1.国家能源集团国能大渡河流域水电开发有限公司, 成都 610016; 2. 电子科技大学信息与软件工程学院, 成都 610054)

在当今工业生产系统中,对核心设备的运维大多通过智能管控系统完成,其中对关键设备的智能异常检测是很重要的环节,会直接影响到工业生产系统的工作效率。设备的维护不足可能会造成巨大的经济损失,而过度维护又会浪费不必要的人力物力资源,因此需要通过智能管控系统及时识别和处理关键设备故障,才能避免生产受到影响而带来经济损失。

动态异常检测是工业制造领域的一个重要研究领域。国内外学者以及研究人员在这一领域都进行了广泛而深入的研究。在国外,近年来随着深度学习技术的发展,基于深度学习的异常检测方法逐渐成为研究热点[1-5]。在国内,目前学者对动态异常检测的研究主要集中于对时间序列建模的研究,主要方法包括时间序列降维、隐空间特征提取以及时序深度学习模型等[6-13]。

然而,现有的工业异常检测方法仍存在一些不足。首先,由于工业生产过程的复杂性和多变性,工业设备的动态运行参数大多为高维复杂时序数据,现有的异常检测算法往往不能满足异常检测任务实时、可靠的需求。其次,异常检测算法的可解释性也需要进一步提高,以便能识别并解释异常问题,从而为工业设备的实际维护工作提供可靠依据。

因此,针对工业设备运行动态参数数据量大、数据维度较高的特点,现提出一种基于耦合函数的动态参数异常检测方法,利用联合分布的耦合函数简单高效地完成对整体时序数据的建模。在具体算法设计中,采用无参数的经验估计法来构建耦合函数,进一步提升算法的整体效率。同时,在此基础上构建概率模型,使得模型具备一定的可解释性。为了验证该方法的有效性,对大渡河流域水电站排水系统的厂房渗漏排水泵动态参数进行异常检测。对算法进行可解释性分析,验证方法自身的可靠性,也为排水泵类设备后续的维护提供重要的参考依据。

1 相关工作

在近年来,许多专家学者针对不同种类的异常提出了不同的异常检测方法,这些方法的原理不尽相同[9]。为了找出适合排水泵动态参数异常检测这一问题的方法,首先对异常的类型进行了探究,之后研究了现有方法的基本原理及其它们的优势与不足。

1.1 异常概述

在数据挖掘和统计学领域中,异常也被称为偏差、离群值。异常大多是由于系统故障而产生,但也有人为因素故意造成的异常,即欺诈。在数据层面,与正常值相比异常值数量更为稀少,但往往能反映出系统的漏洞,更具有研究价值。因此异常检测是一项重要的课题,目前,在数据科学以及应用领域已经受到广泛且深入的研究。

异常可以被大致分成三类:点异常、条件异常和集合异常[10]。点异常表示随机发生的偏差。条件异常表示在特定的时间或空间中表现出的偏差,不同于点异常,它需要一定环境条件的约束,通常出现在时序数据中。集合异常表现为由正常点组成的集合会在一组数据中表现为异常,通常出现在交易欺诈中。

对于动态运行参数来说,它属于时序数据,其中发生的异常可以看作是条件异常。但由于条件异常问题的处理较为复杂,通常通过数据处理,将其转换为点异常问题进行分析。

1.2 异常检测方法概述

1.2.1 经典异常检测方法

经典异常检测方法主要利用了机器学习,通过历史数据来检测异常,主要分为以下四类。

(1)基于距离的方法。这种方法主要通过计算数据点之间的距离来判断异常,最常用的是K-近邻(k-nearest neighbor,KNN)算法[11]。

(2)基于密度的方法。这类方法也是最早的异常检测方法之一,其核心思想认为正常值通常位于高密度区域,而异常值位于低密度区域。局部异常因子算法(local outlier factor,LOF)是最早被提出的这类算法,它在KNN的基础上加入了局部密度理论。此后,一些基于LOF的改进算法也被相继提出,例如连接异常因子(connectivity outlier factor,COF)分析算法,局部相关积分(local correlation integral,LOCI)算法、被动式异常因子分析(influenced outlierness,INFLO)算法等。

(3)基于统计的方法。这类方法依赖于数据分布建模,通过模型检测数据点间的关系从而发现异常。具体包括核密度估计(kernel density estimation,KDE)为代表的无参数方法以及为混合高斯模型(Gaussian mixture model,GMM)为代表的有参数方法。

(4)基于集成的方法。这类方法使用决策树,通过组合不同的子模型,从而提高整体模型的泛化能力和健壮性。主要包括极端梯度提升异常检测(extreme gradient boosting,XGBoost)算法[14]和孤立森林(isolation forest,iForest)算法。

以上经典的异常检测算法虽然在工业领域的动态异常检测上应用广泛,但在面对高维数据时容易陷入高维灾难,具体表现为计算复杂度提高,算法效率以及准确率下降。

1.2.2 基于学习的异常检测方法

这种方法基于深度学习或主动学习,使用这些学习方法去构建不同的分类模型,以达到异常检测的目的。近年来,在各种领域中,深度学习都取得了很高的关注度,在异常检测领域也不例外。深度学习的方法适用于异常检测的各类情形,尤其适用于大规模数据。深度学习方法一般分为有监督的、半监督的和无监督的方法。其中半监督的和无监督的方法受到广泛使用,主要原因在于异常标签数据的缺乏和数据集类别的不平衡性,这些因素会导致有监督的方法表现欠佳。在无监督方法的模型中,自动编码器(auto-encoder)最为常见。此外,在针对时间序列类型数据的情形下,传统的长短期记忆(long short-term memory,LSTM)模型以及循环神经网络(regression neural network, RNN)同样能够发挥重要作用[10]。

基于深度学习的方法可以提取出数据集深层次特征,能够更好地适应大规模数据。不过,这类方法通常具有较高的计算复杂度,并且大多数深度学习的方法缺乏可解释性。

1.3 具体问题定义

水泵厂房场景如图1所示。排水泵类设备具有用途广、分散性强的特点,在水电站的发电水轮机和检修系统中均有分布,排水泵出现异常会直接影响到发电系统的工作效率。通过多次对大岗山水电站的排水系统进行实地考察及数据调研,发现排水泵是否异常与其运行的各项相关参数(如:电压、电流等)有紧密联系。具体来说,排水泵在工作期间会因各种外界因素或自身因素出现无法正常工作或工作效率下降的情况,此时水泵的动态运行参数很可能出现了异常。如果短时间内各项动态运行参数出现多次异常,可以表明排水泵整体出现了异常。

图1 大渡河流域水电站排水系统水泵厂房图Fig.1 The photo of drainage system water pump plant in the hydropower station of Dadu River Basin

2 算法设计

2.1 异常检测方法设计

通过对排水泵的实时数据采集,得到电气属性参数、出口压力参数等多种动态运行参数。这些动态参数可以反映水泵运行情况,如果某一项或某几项动态参数出现异常,那么排水泵也会有很大概率出现异常。

由此,设计了一种从实时和整体两个角度检测排水泵异常的方法。

实时运行状况检测方法:在固定的时间间隔对动态运行参数进行采样,对每次采集的各项参数进行异常检测。

整体运行状况检测方法:一次性采集排水泵一个工作周期内的动态运行参数,计算出这段周期内每项参数的均值方差等统计特征,对各项统计特征进行异常检测。

实时检测可以及时发现排水泵的异常,而整体检测可以评估排水泵工作的稳定性,为后续设备维护提供参考依据。这两个部分的检测结果将共同作为判断排水泵异常的依据。

具体地,实时运行状况检测方法每间隔20 s采集排水泵工作期间的10维动态运行参数,分别为三相电流(Ia,Ib,Ic)、三相电压(Ua,Ub,Uc)、三相线间电压(Uab,Ubc,Uca)和出口压力(fo)。将这些数据作为样本X(X∈Rn×d,d=10),使用异常检测方法进行检测后得到异常分数S(S∈Rn×1)。通过设定阈值,对异常分数进行二分类,分数超过阈值的样本判定为异常。类似地,整体运行状况检测方法只是更换了样本数据,采集排水泵一个工作周期内的进出水速度(si,so)、电流的均值和方差(Iam,Icm,Iavar,Icvar)、电压的均值和方差(Uam,Ubm,Ucm,Uavar,Ubvar,Ucvar)、出口压力的均值和方差(fom,fovar),共14维数据。

2.2 算法基本原理

2.2.1 基于联合分布的异常检测思想

基于统计的异常检测使用概率分布对观测数据进行建模,然后可以根据数据分布模型的关系将某些符合条件的观测点标记为异常。

在一维的情况下,对于任意一个数据点xi,如果xi是异常点,它会处于其分布的概率密度函数的高密度区域之外,也就是尾端概率P(X≤xi)或P(X≥xi)的数值会非常小。那么在其累积分布函数FX中,FX(xi)和1-FX(xi)的数值就会非常小。因此,累积分布函数中FX(xi)和1-FX(xi)的数值可以作为判断异常的重要依据。类似地,对于多维数据,也可以使用这样的方法来判断异常。然而在多维情况下仅仅依靠单变量的边缘分布函数是不够的,这忽略了变量之间的依赖关系,这种依赖关系在水泵的异常检测中是极其重要的。例如,由于启停水泵的操作,三相电流与出口压力的变动往往是协同的,当两者的数据变动差异较大时,则可能出现异常。为此,在多维数据的情况下,通过多维变量的联合分布函数进行建模计算尾端概率。

通常而言,对数据的联合分布进行建模是一个复杂的问题,基于耦合函数(Copula)的方法可以解决这一问题,并在此基础上进行异常检测。

2.2.2 基于Copula的联合分布建模

Copula是统计学中一种用来处理随机变量相关性问题的工具,它可以将一个多维随机变量的联合分布分解为它们各自的边缘分布和一个Copula函数的形式[12]。具体地,在联合分布建模的过程中,排水泵的动态参数数据矩阵可以写为(X1,X2,…,Xi,…,Xd),其中Xi表示每一类动态参数的数据向量,它们的边缘分布Fi(x)=P(Xi≤x)连续,因此可以对它们使用反变换法,可得

(1)

通过式(1)的变换,可以得到随机向量U=[F1(X1),F2(X2),…,Fd(Xd)]。这样数据矩阵(X1,X2,…,Xd)的Copula函数就表示为随机向量(U1,U2,…,Ud)的联合分布函数,即

C(u1,u2,…,ud)=P(U1≤u1,U2≤u2,…,

Ud≤ud)

(2)

根据Sklar定理,任意的联合概率分布函数可以被写为单变量边缘分布函数和一个描述它们之间依赖结构的Copula函数。使用Copula函数来捕捉多个单变量之间的依赖关系,并构建联合分布为

F(X)=C[F1(x1),F2(x2),…,Fn(xn)]

(3)

式(3)中:F(X)为联合分布函数;C(·)为Copula函数。

在根据动态运行参数检测排水泵异常的问题中,使用Copula函数将多个不同的动态运行参数的边缘分布进行建模,构造一个整体的多维数据的联合分布。联合分布的相关性性质仅由Copula函数决定,这使得在对排水泵动态运行参数这种高维度数据建模时更加灵活高效。具体说来,对每一个维度分别建模,得到每个维度的边缘分布,最后通过Copula函数将它们联系在一起,得到关于多种动态运行参数的多维随机变量的联合分布。这个联合分布能够考虑到各个参数分布之间的相互关联,构建更准确的后验分布。

2.2.3 经验Copula估计方法

通过以上Copula函数的性质可知,对数据的联合分布进行建模需要获得数据的Copula函数的具体形式,因此首先需要找到合适的Copula函数估计方法。

Copula函数有多种表达形式,其中有些具有固定的函数形式,例如椭圆Copula函数簇、阿基米德Copula函数簇等,这些有固定形式的Copula函数通常带有一个或多个参数。还有的Copula函数没有固定的表达形式,它们可以由观测数据构建,这称为经验Copula函数[15]。

对于Copula函数的估计,基于现有的理论有参数法、半参数法和无参数法[16]。参数法和半参数法通常使用形式固定的Copula函数,通过极大似然法计算其中的参数。然而,当数据维度过高时,这两种方法的优化过程会变得十分复杂,容易遭受高维灾难。相对地,无参数法可以构建经验Copula函数,它在高维数据的情况下表现更好,具有更强的泛用性。因此,采用基于无参数的经验Copula函数估计方法实现异常检测。

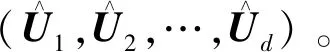
(4)

式(4)中:I(·)为指示函数。

(5)

2.3 算法描述

在上述基于经验Copula的排水泵动态运行参数异常检测算法的基础上,根据实际问题的需要,进行了如下修改,最终的算法流程如算法1所示。

算法1基于经验Copula的动态运行参数异常检测算法

输入：由排水泵动态运行参数组成的多维观测值矩阵X∈Rn×d,经验分布函数计算函数eCDF(·),偏度计算函数Skew(·)

输出：排水泵的异常分数向量S∈Rn×1

(1)forj←1 toddo

(2)end for

(3)fori←1 tondo

ifbd<0

else

(4)end for

(5)returnS=(s1,s2,…,sn)

在实际应用中,数据的概率分布通常具有不对称性。分布的主体不一定位于中央,其概率密度函数的长尾部可能在左侧,也可能在右侧,如图2所示。此时,如果使用单一的尾端概率作为异常检测的标准,就可能出现误判的情况。因此,需要首先了解数据分布不对称性的情况,从而选择合适的尾端概率作为异常检测的参考。式(6)用于计算数据分布的偏度。当偏度值为负时,分布左偏,意味着左尾部更长,此时应该参考左尾端概率进行异常检测。同样地,当偏度为正时,分布右偏,意味着右尾部更长,此时应该参考右尾端概率进行异常检测。因此在异常检测算法中,先分别计算了左尾端概率分布和右尾端概率分布,然后根据偏度的正负选择合适的分布作为异常分数计算的参考依据。

图2 分布函数左偏和右偏示意图Fig.2 The schematic diagram of positive and negative skewed distribution function

(6)

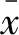
在最终结果的表现上,通过计算尾端概率可以将该观测值的异常程度量化,概率越小说明该值越可能为异常。然而这样获得的异常值是一个概率值,其取值区间为[0,1],取值的分布区间过于集中,容易引发数值计算上的问题。由此,采取了将概率值取负对数的方法,将异常值区间转换到[0,+∞),并将该值作为异常分数。概率值越小,异常的可能性越大,相应地,异常分数也会越大。

3 实验及结果分析

3.1 数据集介绍

首先采集了2018—2020年大渡河流域水电站中三台渗漏排水泵的历史动态运行参数。针对实时和整体运行状况,进行了不同的数据预处理,得到了数据集(Ⅰ)和数据集(Ⅱ)。

根据2.1节的实时运行状况检测方法,把在三台排水泵上采集的电压、电流等数据处理后作为数据集(Ⅰ)。具体信息如表1所示。

表1 数据集(Ⅰ)基本信息Table 1 The basic information of dataset(Ⅰ)

根据2.1节的整体运行状况检测方法,把在三台排水泵上采集的电压、电流等数据的统计特征进行处理,得到数据集(Ⅱ)。具体信息如表2所示。

表2 数据集(Ⅱ)基本信息Table 2 The basic information of dataset(Ⅱ)

3.2 评价标准

异常检测问题可以看作是一个二分类问题,即分为异常和正常两类,可以使用二分类问题中的评价标准。不同的是,检测到异常为正例,而检测到正常为负例,通常正例数目要远小于负例数目。在最终结果中,记录算法判定为异常且实际为异常的数目(true positive,TP),判定为异常而实际为正常的数目(false positive,FP),判定为正常且实际为正常的数目(true negative,TN),判定为正常而实际为异常的数目(false negative,FN)。由于异常检测问题样本的不平衡性,需要计算精确率(precision,P)和召回率(recall,R),如式(7)和式(8)所示。为了综合考虑精确率和召回率带来的影响,选择了平均精确率(average precision,AP)作为算法的评价指标。

(7)

(8)

除此之外,还计算了曲线下的面积(area under curve,AUC)值。对于分类器的接受者操作特征(receiver operating characteristics,ROC),平面的横坐标是FP率,纵坐标是TP率。可以根据算法在测试样本上的表现得到一个TP率和FP率点对,这样该分类器就可以映射成ROC平面上的一个点。调整这个分类器进行分类时使用的阈值,就可以得到一条ROC曲线。AUC值取值在0.5～1,其数值越接近1表示算法表现越好。

为了衡量算法运行效率,还选择了运行时间作为评价指标,在相同计算资源、相同实验数据集的条件下,运行时间越短表示算法效率越高。

3.3 对比算法

选取了以下4种常用的,并且基于不同原理的异常检测算法和本文算法进行比较。

(1)K-近邻(KNN)算法,一种基于距离的异常检测算法[17]。

(2)连接的异常因子分析(COF)算法[18],一种基于密度的异常检测算法。

(3)基于角度的异常检测(ABOD)算法[19],一种基于统计的异常检测算法。

(4)孤立森林(iForest)算法[20],一种基于集成的异常检测算法。

3.4 实验结果分析

对比算法的ROC值、AP值如图3和图4所示,在数据集(Ⅰ)上的运行时间如表3所示。

表3 各算法在数据集(Ⅰ)上的运行时间Table 3 The running time of each algorithm on dataset (Ⅰ)

图3 各算法在数据集(Ⅰ)上的表现Fig.3 The performance of each algorithm on dataset (Ⅰ)

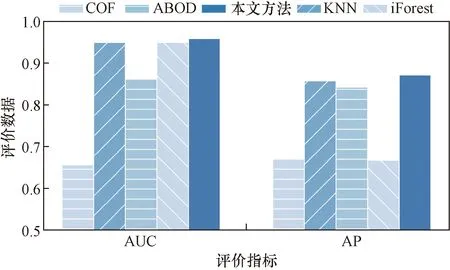
图4 各算法在数据集(Ⅱ)上的表现Fig.4 The performance of each algorithm on dataset (Ⅱ)

从实验结果可以看出,对于在数据集(Ⅰ)上进行的实验,基于Copula的算法总体表现最好:其中AUC值为0.987,比表现排名第二的KNN算法高1.96%;AP值为0.873,和表现最高的iForest算法相比仅低8.49%;运行时间仅为0.781 s,在所有算法中最短。

具体分析数据集(Ⅰ)的结果可以发现,从AUC和AP两个指标来看,iForest算法和基于Copula的算法表现较佳,这是因为iForest算法可以通过控制二叉树的数量,使算法表现变得稳定,而基于Copula的异常检测算法能够建模联合分布,因此算法性能也较好。而COF算法本身用于处理低密度下的异常值,随着数据量以及数据维度的增加COF算法表现显著下降。KNN算法则无法找出局部异常点,同样不能达到最优表现。从算法效率来看,由于高数据维度的影响,计算数据点的距离或密度函数的计算复杂度变大,基于距离的算法KNN和基于密度的算法COF运行时间显著变长,基于集成的算法iForest具有线性复杂度,运行时间相对较短。因为采用了无参数的经验估计法,基于Copula的异常检测算法效率明显优于其他算法。

对于在数据集(Ⅱ)上进行的实验,与在数据集(Ⅰ)上的实验不同的是,数据集(Ⅱ)的数据维度更高,高维度的影响使得所有算法的表现均有所下降,其中基于Copula的算法总体表现下降最少,AUC值下降了2.83%,AP下降了0.23%。这体现了基于Copula的算法对高维度数据具有更强的适应性。在数据集(Ⅱ)上并没有比较运行时间,这是由于数据集(Ⅱ)数据量较少,各算法在运行时间上相差无几。

3.5 可解释性分析

在实时运行状况检测中,算法的最终结果是一个整体的异常分数,但仍然可以在计算过程中获得各个维度单独的异常分数,对于10维度的数据点xi,可以得到10个维度的异常分数si=(s1,s2,…,s10)。它可以描述在异常发生时,哪个维度的数据对整体异常的贡献最大,这为更加精确地定位异常提供了重要的依据。由此,任意选取实验中两个标为正常和异常的数据点,得到异常分数对比图。如图5所示,对这一可解释性结果进行描述,其中95%为数据集中正常数据的比例。

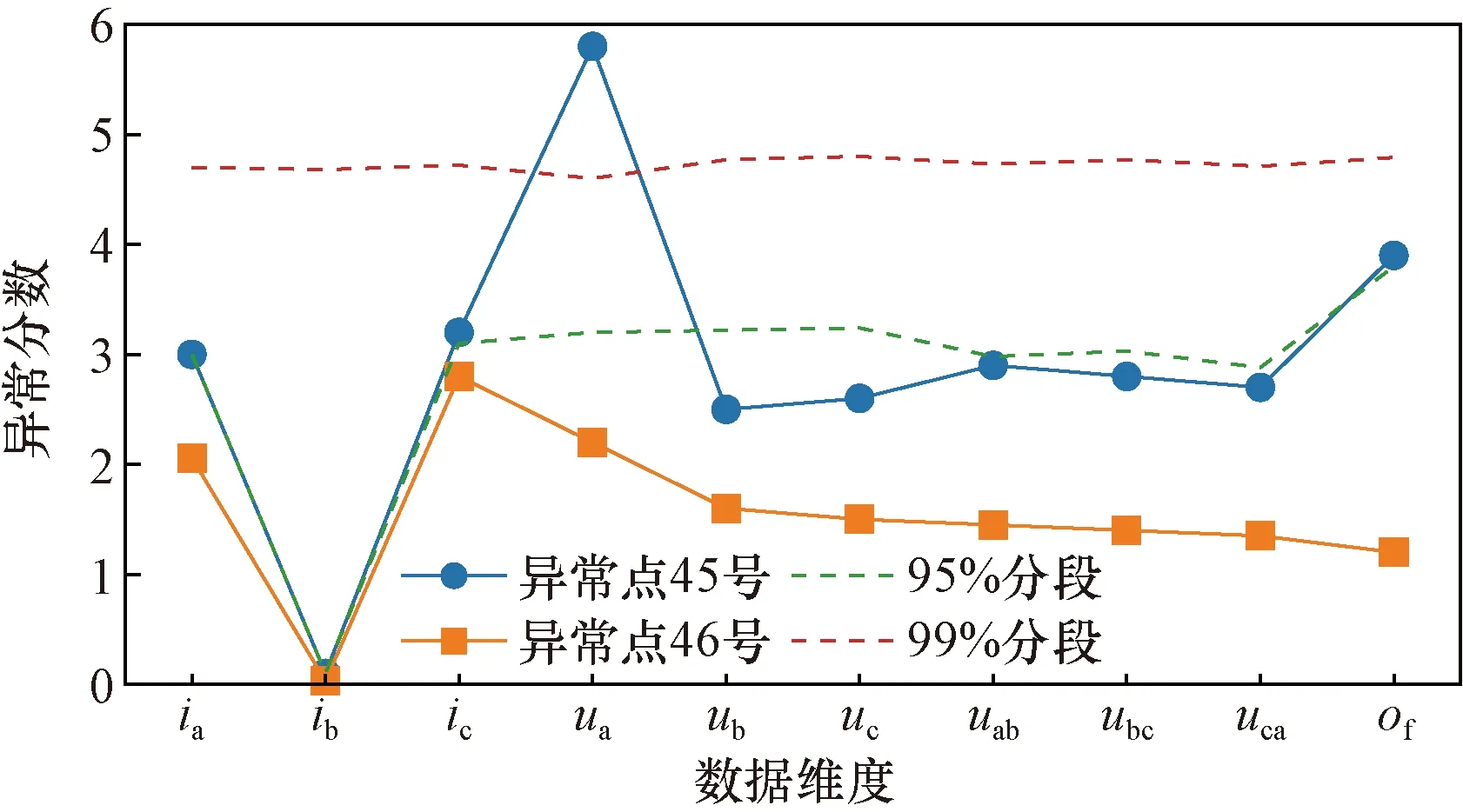
a,b,c为三相线;i为对应相的电流;u为电压;uab,ubc,uca为相应的线电压;of表示出水口压力图5 异常分数对比图Fig.5 Anomaly score comparison diagram

可以发现,正常点46号的所有特征的异常分数全部在95%临界线以下,而异常点45号的特征ua的异常分数已经超过99%临界线,特征of的异常分数超过了95%临界线。这表明在数据点45号采集时,排水泵的A相电压和出口压力很可能出现了异常,这些异常很可能会在后续导致排水泵整体工作异常,这使得工作人员的故障排查能够更具有目的性。

4 结论

提出了一种基于经验估计耦合函数的动态参数异常检测方法。首先对大渡河流域水电站排水泵开展实地数据调研,具体分析了排水泵动态运行参数,通过对时序数据采样,将问题转化为点异常检测问题进行研究。之后根据基于联合分布的异常检测方法,使用了经验Copula函数这一数学工具对数据分布进行建模,完成了异常检测任务。对比实验显示,算法具有最优的算法性能并较大地提升了算法效率。最后,对异常检测结果进行可解释性分析,证实了本文方法的可靠性,且该方法能够为故障排查和后续维护提供重要依据。

研究仍存在数据丰富度不足的问题。在数据调研与采集的过程中,只能从水电站数据中心获得部分类别的水泵动态运行数据,其中大部分是电气属性相关的数据。根据泵类设备研究经验,对水泵运行影响较大的参数包括电机转子振动或温度等参数。采集这些数据并进行分析可以更加全面地检测排水泵故障,从而提高方法整体的可靠性。针对以上的不足,将在以后的研究工作中进行进一步改进与优化。