气藏直定井温度剖面影响规律分析

马寒松, 李海涛, 罗红文*, 向雨行, 刘文强, 粟超, 张琴, 李颖

(1．西南石油大学油气藏地质及开发工程国家重点实验室, 成都 610500; 2．中国石油集团测井有限公司, 西安 710077; 3．中国石油集团川庆钻探工程有限公司地质勘探开发研究院, 成都 610051)

基于分布式光纤温度监测(distributed temperature sensing,DTS)的井下测温技术正逐渐被应用于油气井井下动态监测[1-2],特别是针对水平井,根据获得的数据资料,DTS技术可以识别人工裂缝[3]、判断流体类型[4]、评价压裂改造效果[5],而且还可以对压裂水平井产出剖面、裂缝流量贡献及裂缝参数等进行定量解释[6-8]。影响气藏直定井温度剖面的因素众多且规律复杂,致使基于DTS的气藏直定井产出剖面、裂缝参数的定量解释有一定的困难。因此,首先要实现气藏直定井温度剖面预测并确定气藏直定井温度剖面的主导因素。国内外学者在直井和水平井温度剖面预测方面做了许多研究。Cui等[9]基于三线性流假设,首次建立了人工裂缝温度分布计算模型,模型中考虑了焦耳-汤姆逊效应和摩擦生热引起的微小温度变化,但仅能模拟单相流的情况,分析了人工裂缝内流体温度对裂缝参数的敏感性。Yoshida等[10]考虑了黏性耗散和流体热膨胀等微量热效应,建立了一个单相气藏压裂水平井温度预测模型,并将气藏和井筒模型进行了耦合求解,通过温度剖面理论模拟表明压裂水平井温度剖面对人工裂缝参数较为敏感,据此提出水平井压后温度监测具有帮助诊断人工裂缝参数的潜能。Cai等[11-12]以Li等[13]的井筒模型为基础,并将其与油藏和气藏温度模型相耦合,分别建立了单相油藏、气藏水平生产井的温度剖面预测模型,模拟了不同射孔方案时水平井温度分布。Yoshida等[14-15]将他们之前建立的单相温度模型扩展为多相,建立了多相压裂水平井温度模型用以计算水平井生产时的井筒温度剖面以及关井时的近井储层温度分布,认为水平井压裂后仍将地温当做初始温度是不合理的,通过现场实例对模型进行了验证。朱世琰[16]建立了油水两相水平井温度剖面预测模型,讨论了不同因素对水平井温度剖面的影响规律;罗红文等[17]建立了考虑多种微热效应的低渗气藏压裂水平井温度剖面预测模型,并分析了产水量分布等对井筒温度剖面的影响规律;吴木旺等[18]考虑流体渗流过程中焦耳汤普逊效应以及诸多微量热效应,结合质量守恒、动量守恒、能量守恒定律建立了低渗多层合采气井温度剖面预测模型,分析讨论了产量、生产时间和渗透率对产出温度剖面影响。可见,国内外学者在油气井温度剖面模拟分析方面做了大量研究,但现有模型多针对水平井,对多产层气藏直定井的特点考虑不足,且针对气藏直定井温度剖面影响规律方面的研究较少。

因此,现针对多产层气藏直定井特点,基于质量守恒和能量守恒,建立一套多产层气藏直定井温度剖面预测模型,通过耦合求解,模拟分析多产层气藏直定井温度剖面分布特征及影响规律,并采用正交试验分析法评价不同因素对气藏直定井温度剖面的影响程度,明确影响气藏直定井温度剖面的主导因素,以期为实现基于DTS监测定量解释气藏直定井产出剖面、储层特征参数等奠定理论基础。

1 气藏直定井温度剖面预测模型

1.1 气藏模型

1.1.1 气藏渗流模型

根据质量守恒定律,引入拟压力函数,考虑地层渗透率的各向异性,建立如下气、水两相三维非稳态渗流方程。

1)气相

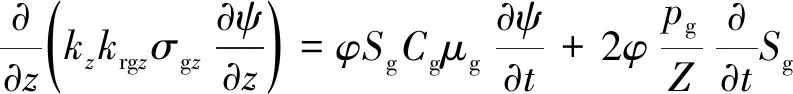
(1)

2)水相

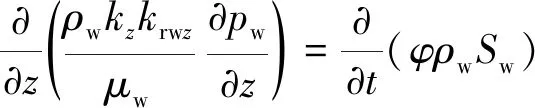
(2)

式中:ρw为水密度,kg/m3;φ为孔隙度;Sg、Sw分别为气、水饱和度;k为地层渗透率,D;kro、krw分别为油、水的相对渗透率;μg、μw分别为油、水的黏度,mPa·s;pg、pw分别为油、水的压力,MPa;σgx、σgy、σgz分别为x、y、z方向的气相非达西因子;g为重力加速度,9.8 m/s2;Z为垂直定井深,向下为正,m。

3)边界条件

边界条件包括外边界条件和内边界条件,外边界条件表示气藏外边界所处的状态;内边界条件表示气藏内部的井筒所处的状态。所建模型为封闭气藏,所取的外边界为封闭气藏外边缘,此处的温度和压力均为恒定地层温度和压力,所以变化率为0;内边界指的是裂缝与井筒接触面,两者温度和压力相等,在固井段采用综合传热系数表征井筒与储层的温度。

(1)外边界条件。

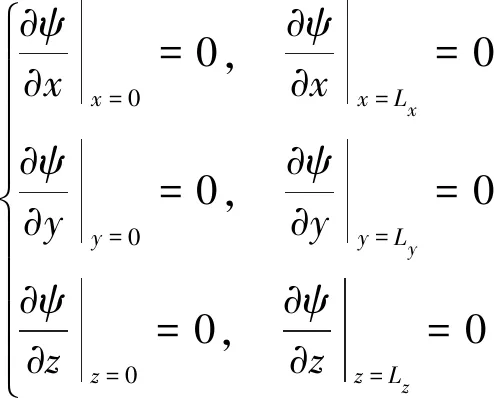
(3)

式(3)中:Lx、Ly、Lz分别为气藏在x、y、z方向的几何尺寸。

(2)内边界条件。

(4)

pw|x=0=pwb

(5)

pg|x=0=pwb

(6)

式中:Pwb为井底压力,MPa;ψwb为井底拟压力函数,MPa2/(mPa·s)。

1.1.2 气藏温度模型

基于能量守恒方程,考虑包括热传导、热对流、焦耳-汤普逊效应、热膨胀和黏性耗散在内的多种微量热效应,建立气藏温度模型为

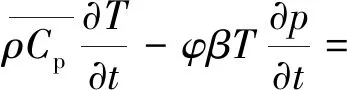
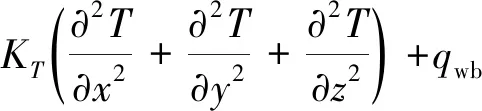
(7)

式(7)中:Cp为热容,J/(kg·K);β为热膨胀系数,K-1;T为储层中的温度,K;ρ为流体密度,kg/m3;k为渗透率,mD;KT为储层热导率,J/(m·s·K);qwb为井筒和储层之间单位体积的热传导速率,J/(m3·s)。

4)边界条件

边界条件包括外边界条件和内边界条件。

(1)外边界条件。

(8)

(2)内边界条件。

(9)

式(9)中:Kt为储层导热系数,W/(m·K);UTt为综合传热系数,W/(m2·K);rw为井筒半径,m;

1.2 井筒模型

基于质量守恒、动量守恒和能量守恒,建立气水两相井筒流动和温度模型。井筒内流体流动方向如图1所示,建模时考虑井筒摩擦、流体混合压降、流体加速压降以及重力作用对井筒压降的影响、忽略井筒中气、水相间的滑脱效应。

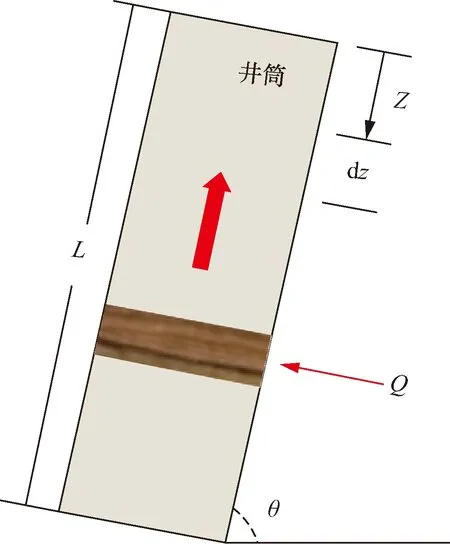
L为井筒长度,m;θ为井筒倾角,(°);Q为产层流入量,m3/d;Z为沿井筒方向;dz为沿Z方向划分的网格长度图1 井筒流动能量守恒Fig.1 Conservation of wellbore flow energy

1.2.1 井筒流动模型

将井筒分为若干段,在井筒任一微元段内,根据能量守恒和动量守恒,井筒压力变化可以表示为

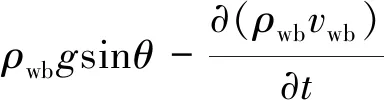
(10)

式(10)中:Rinw井筒内径,m;γ为井筒打开程度;pwb为井筒中的压力,MPa;ρwb为井筒中的流体密度,kg/m3;f为井壁摩擦因数;vwb为井筒中的流体流速,m/s;θ为井筒倾角,(°);g为重力加速度,m/s2。

1.2.2 井筒热学模型

基于能量守恒,忽略流体相间的热传导效应,建立井筒温度模型为

(11)

式(11)中:ρI为流入流体的密度,kg/m3;vI为流入流体的流速,m/s;TI为流体流入温度,K;Twb为井筒中的温度,K;UTt为综合传热系数[19-20],J/(m2·s·K);KJT为焦耳汤普逊系数[21-22],K/MPa。

1.3 气藏与井筒耦合模型求解

气藏和井筒热学模型为相互耦合且非线性的,因此,需要通过迭代实现耦合温度模型求解,建立的气藏直定井温度剖面预测模型耦合求解流程如图2所示。

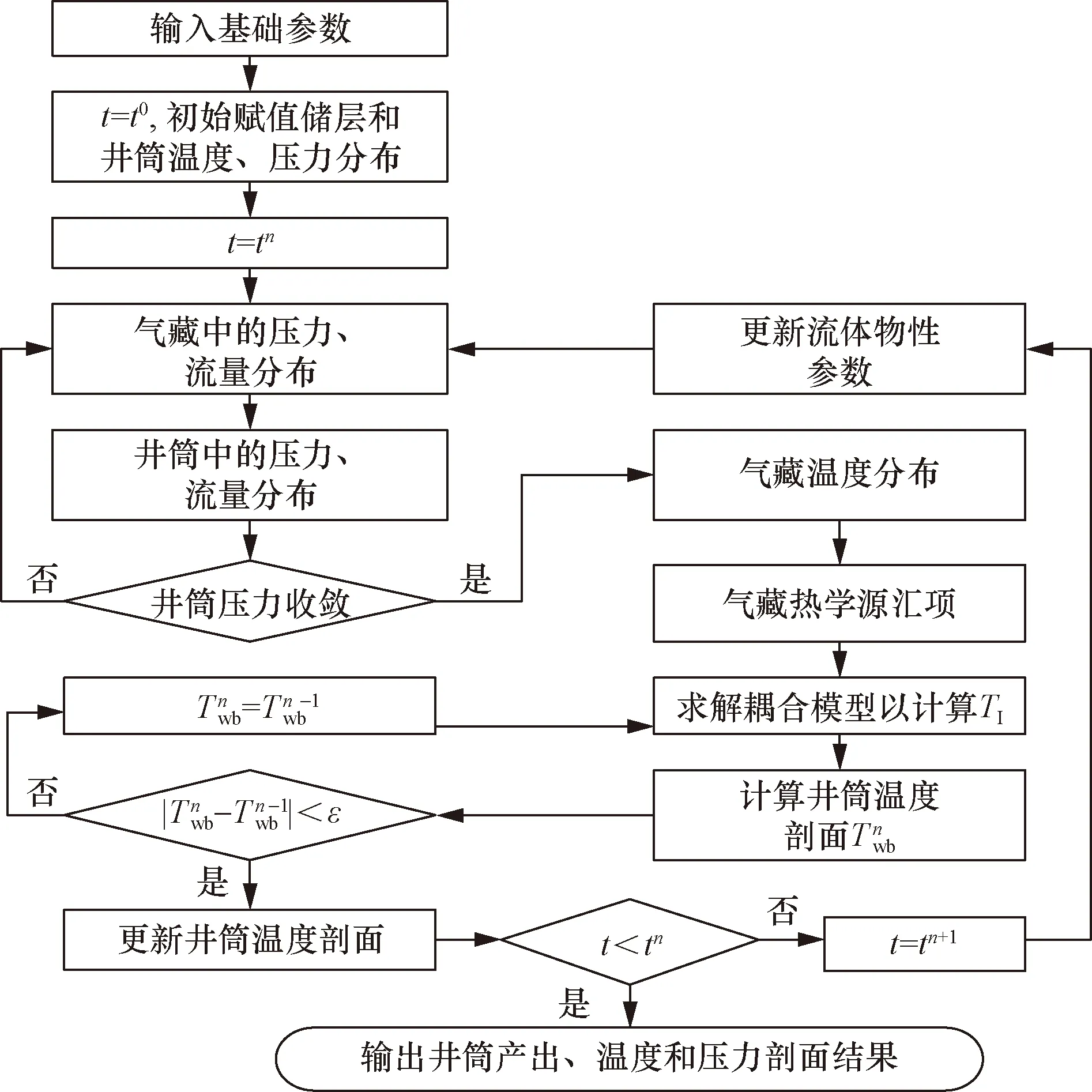
图2 气藏直定井温度剖面预测模型耦合求解思路Fig.2 Calculation flow chart of temperature profile prediction model for vertical well in gas reservoir

2 气藏直定井温度剖面影响规律及敏感参数分析

以一口抽象的多产层气藏直定井为对象,采用所建立气藏直定井温度剖面预测模型对该井温度剖面进行模拟分析,探究不同单因素对多产层气藏直定井温度剖面的影响规律、明确影响多产层气藏直定井温度剖面的主控因素,模拟计算所需基础参数如表1、表2所示,储层岩石热力学参数如表3所示。

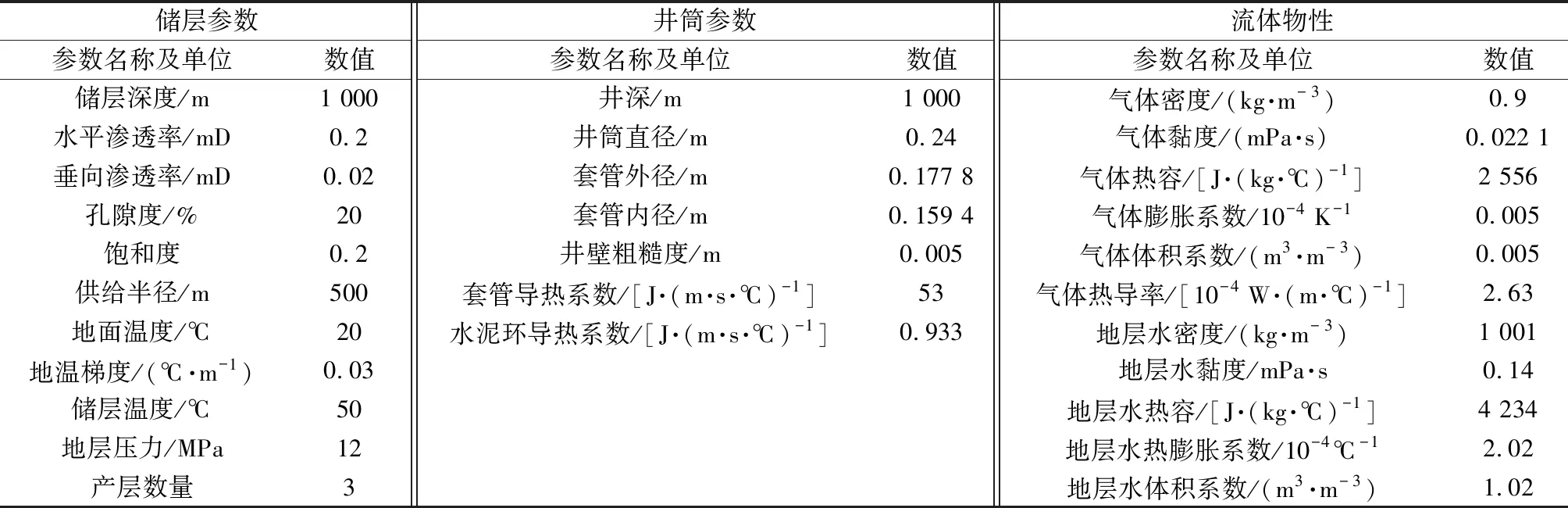
表1 气藏直定井模拟计算基础参数Table 1 Basic parameters for vertical well simulation calculation of gas reservoir

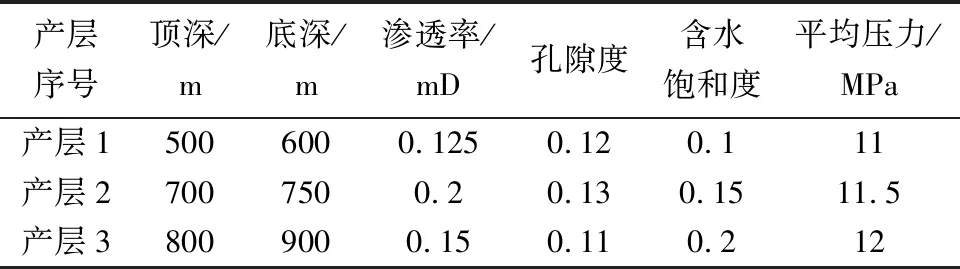
表2 气藏直定井产层基础参数Table 2 Basic parameters of production layer of vertical well in gas reservoir

表3 储层岩石热力学参数Table 3 Thermodynamic parameters of reservoir rocks

2.1 气藏直定井温度剖面单因素影响分析

以上述抽象气藏直定井作为研究对象,通过模拟7个不同单因素情况下该井的温度动态,进而分析不同单因素对气藏直定井温度剖面的影响规律。

如图3(a)所示为不同单井产量下温度剖面模拟结果,可以看出,气藏直定井温度剖面从井底到井口逐渐降低,产层段井筒温度降低速度大于固井段。随着产量的增加,井筒温度剖面整体降低,根据渗流理论,定产生产时,产量越高,井筒压力剖面越低,生产压差必然越大,由于压差引起的焦汤冷却效应就越明显,使得井筒温度越低。图3(b)所示为井筒流量剖面,可以看出,井筒流量剖面呈“阶梯状”,每一“阶梯”的高度就对应着每个产层的产量贡献,各产层的产量贡献总体与渗透率分布呈正相关。

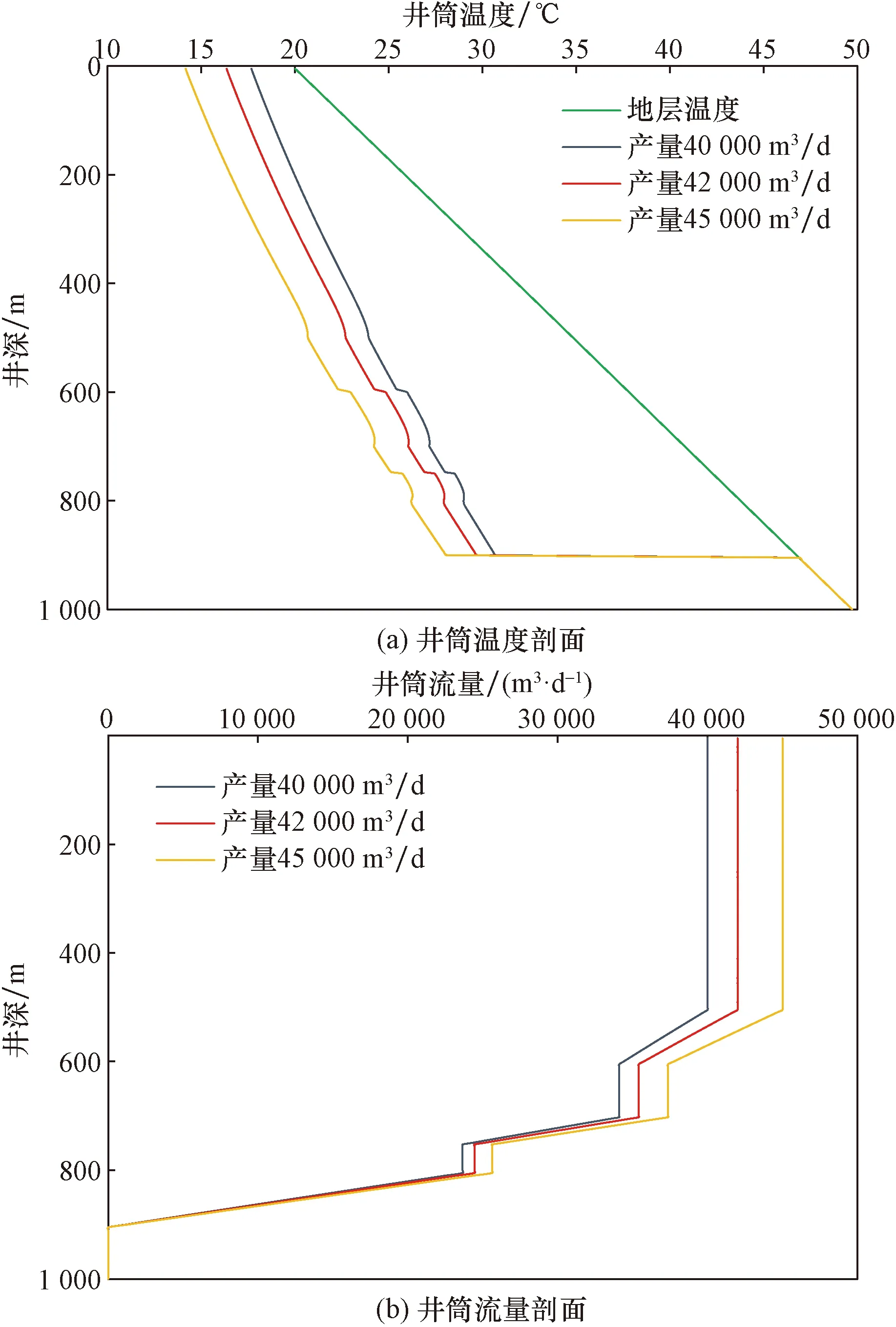
图3 产量对井筒温度、流量剖面的影响Fig.3 Effect of production on wellbore temperature and flow profile

如图4(a)所示为不同储层渗透率下的气藏直定井温度剖面,可知,渗透率越高,井筒的温度剖面越高,但随着渗透率的增加,井筒温度剖面升高速率有所下降。根据渗流理论亦可知,定产生产时,地层渗透率越大,井筒压力越高,生产压差必然越小,但随着渗透率的增加,井筒压力剖面升高速率有所下降,使得流体流动引起的焦汤效应减弱,温度增长速度变慢。图4(b)为井筒产气剖面,可以看出,渗透率对井筒产气剖面的影响较大,各产出产量贡献与渗透率分布呈正相关。

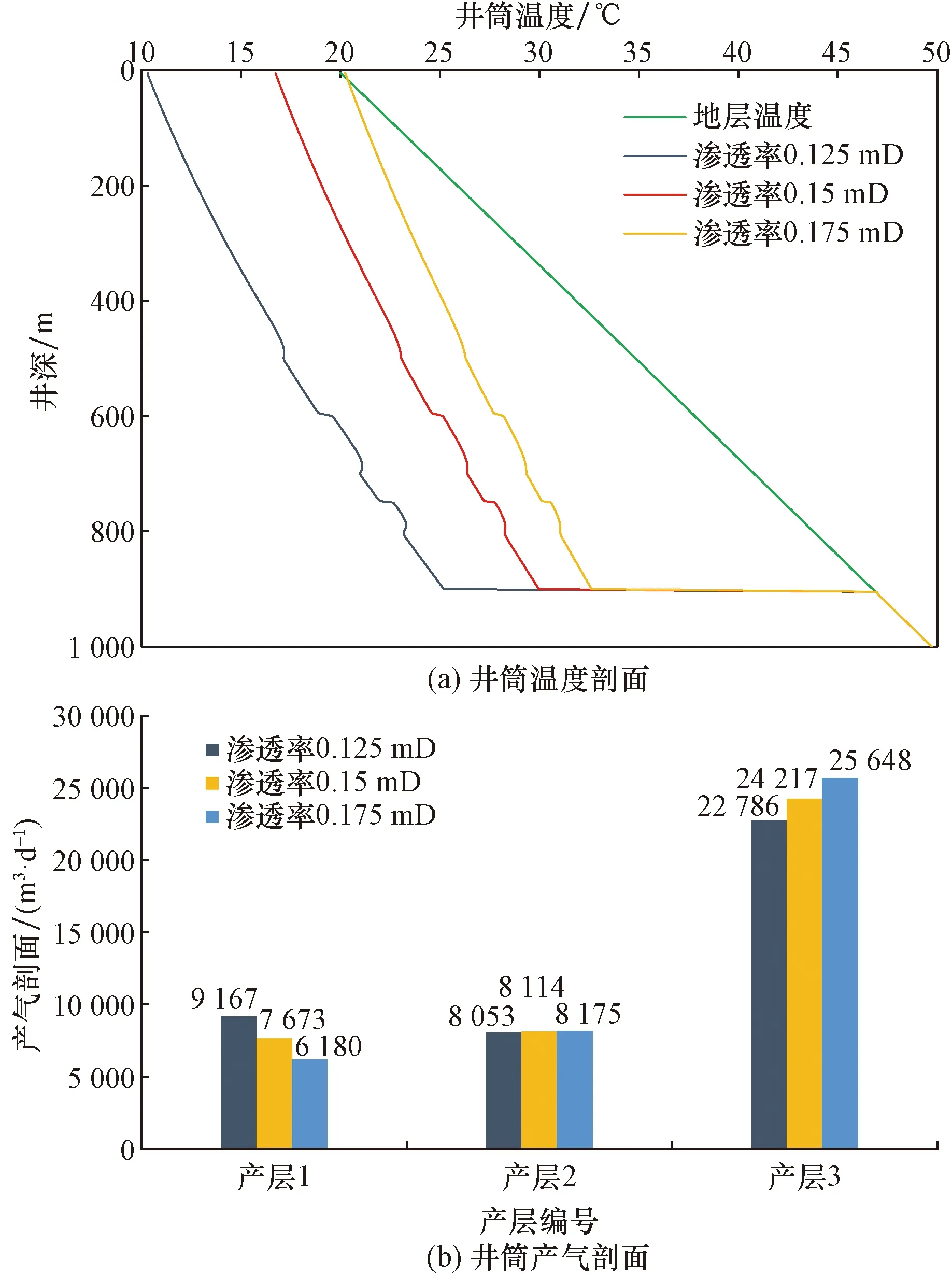
图4 渗透率对井筒温度、流量剖面的影响Fig.4 Effect of permeability on wellbore temperature and flow profile

如图5(a)所示为不同储层导热系数情况下的井筒温度剖面,可以看出,导热系数越大,井筒温度剖面越高,这是因为随储层导热系数的增加,储层中岩石传热效率越高,在单位时间内所传导的热量也随之增大,但储层岩石导热系数对井筒温度剖面的影响总体较小。同时从图5(b)中可以明显看出,导热系数的变化对井筒压力分布以及产出剖面的影响较小。

图5 储层导热系数对井筒温度、产气剖面的影响Fig.5 Influence of reservoir thermal conductivity on wellbore temperature and gas production profile

如图6(a)所示为不同井筒直径情况下的井筒温度剖面,可以看出,井筒温度剖面随井径的增加而整体升高,这主要是因为随着井筒直径的增加,井筒中流体与井壁的摩擦明显减小,降低了井筒中的压降损失,井筒压力剖面越高,生产压差越小,由压降引起的焦汤冷却效应越弱,因此,井筒直径越大,流入温度越高,使井筒温度剖面整体提高。井筒直径改变,对井筒产气剖面略有影响[图6(b)]。

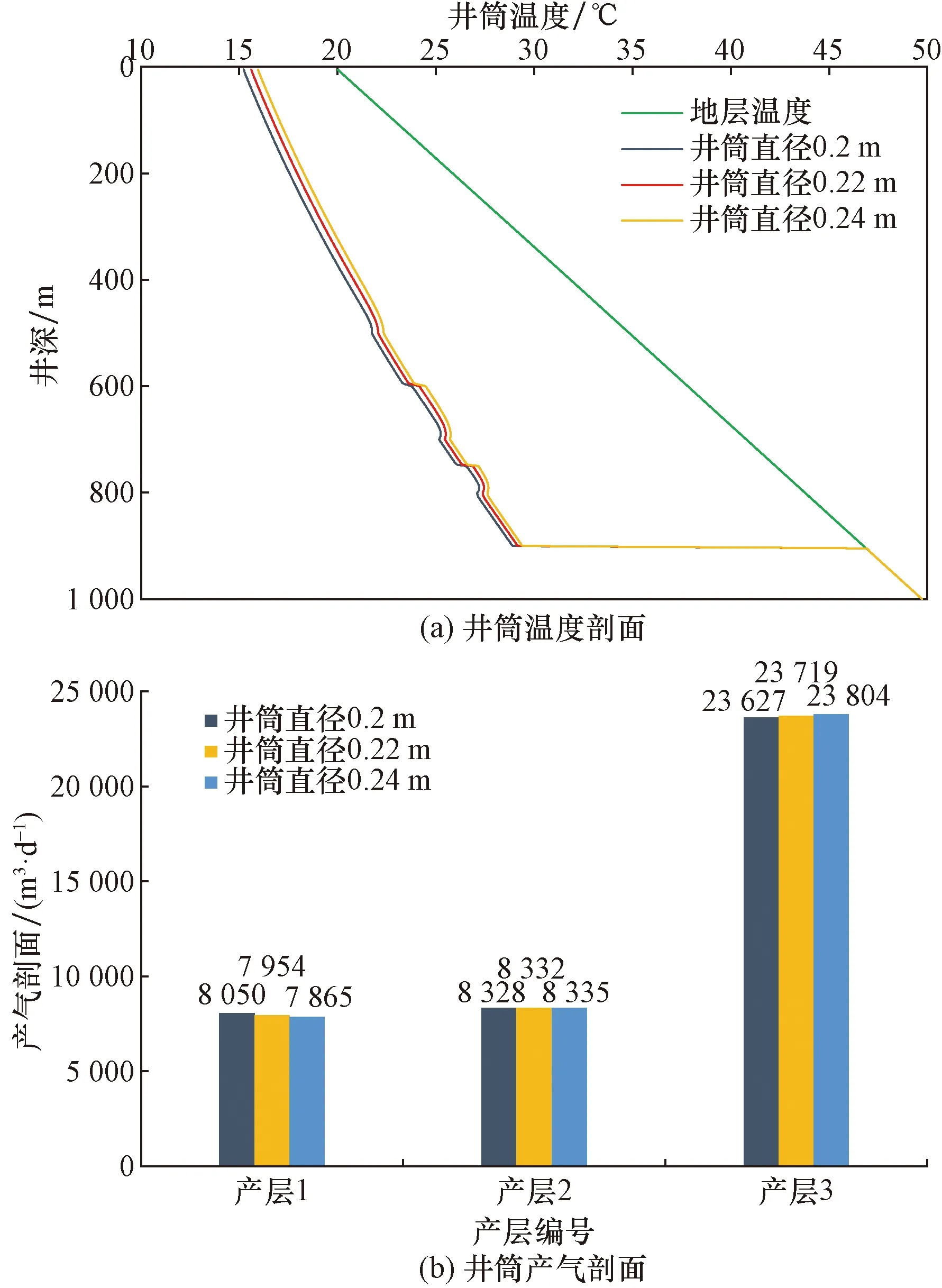
图6 井筒直径对井筒温度、产气剖面的影响Fig.6 Influence of wellbore diameter on wellbore temperature and gas production profile

如图7(a)所示为不同井眼轨迹情况下的井筒温度剖面,可以看出,θ越大,井底温度和靠近井底的产出段井筒温度越低,这主要是由于地温差异导致。但越靠近井口位置,随θ的增加,井筒温度剖面有所降低,由于随θ的增加,井筒压降越小,井筒压力剖面越高,压差越小,导致天然气因压降损失导致的焦汤冷却效应减弱,所以靠近井口位置,θ越大,反而温度越高。井筒产出剖面分布,仍受地层渗透率分布的主导。

图7 井眼轨迹对井筒温度、产气剖面的影响Fig.7 Influence of well trajectory on wellbore temperature and gas production profile

如图8(a)所示为不同含水饱和度情况下的井筒温度剖面,可以看出,井筒温度与储层含水饱和度呈负相关,随含水饱和度的增加,井筒温度剖面降低,这是由于在相同产气量情况下,含水饱和度越高,气相相对渗透率越低,生产压差越大,由于压降引起的气相焦汤冷却效应越强,导致井筒温度剖面降低。产出剖面仍受产层渗透率分布主导,各产层的产气量贡献与产层渗透率呈正相关[图8(b)]。

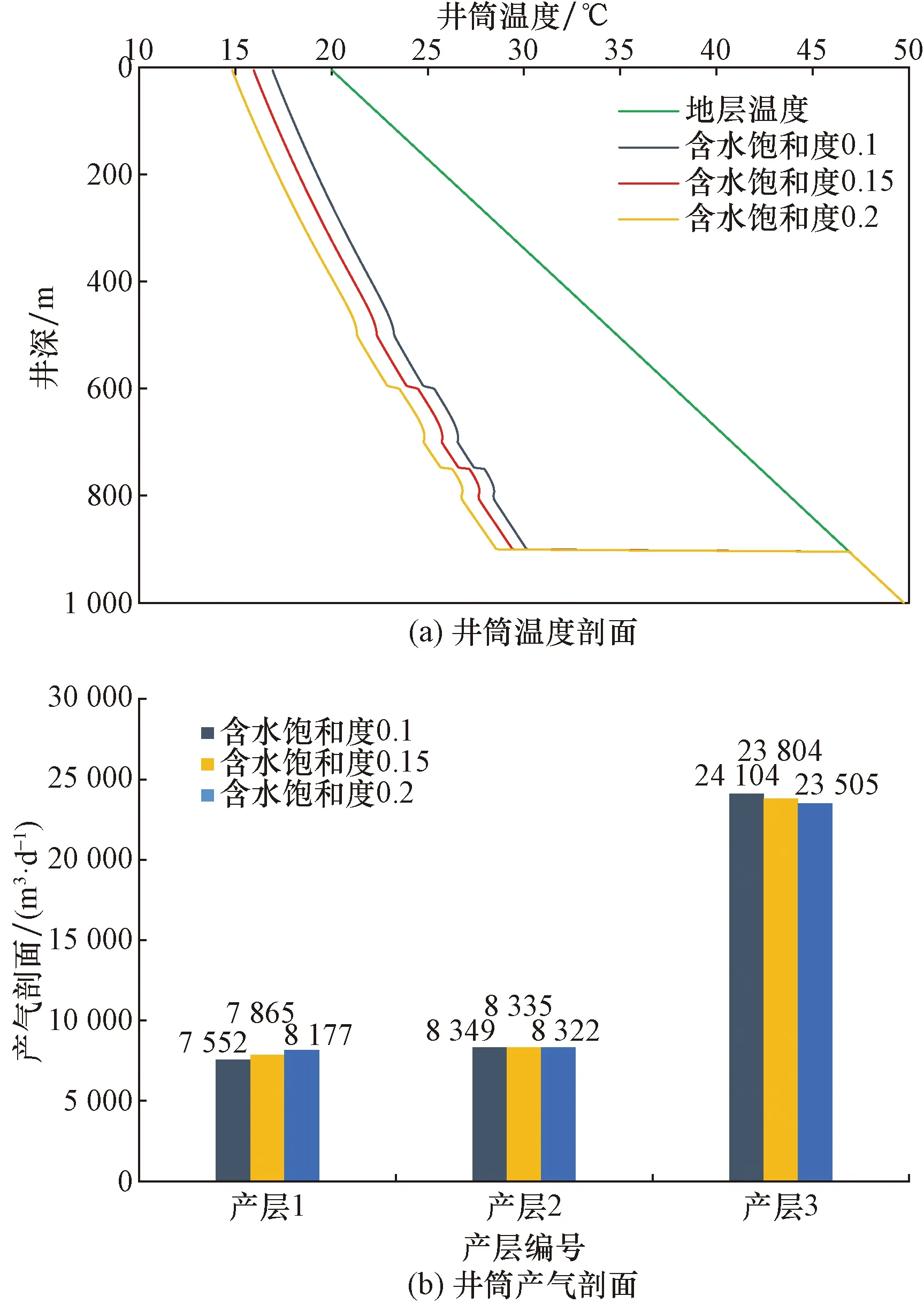
图8 含水饱和度对井筒温度、流量剖面的影响Fig.8 Influence of water saturation on wellbore temperature and flow profile

如图9(a)所示为不同天然气相对密度下的温度剖面变化情况。可以看出,随天然气相对密度的增加,井筒温度剖面整体有所下降,且随着天然气相对密度的升高,井筒温度剖面降低的速度越快。这是因为天然气密度越大,井筒压力剖面越低,生产压差越大,由于压降引起的气相焦汤冷却作用变强,导致井筒温度剖面降低。产出剖面总体受产层渗透率分布控制,各产层的产气量贡献与产层渗透率仍然呈正相关。但随着天然气相对密度的升高,越靠近井底的产层段产量贡献略有降低,越靠近井口的产层段产量贡献有所升高[图9(b)],这主要是由于井筒压力剖面变化,引起各产层段对应的生产压差发生变化所导致的。

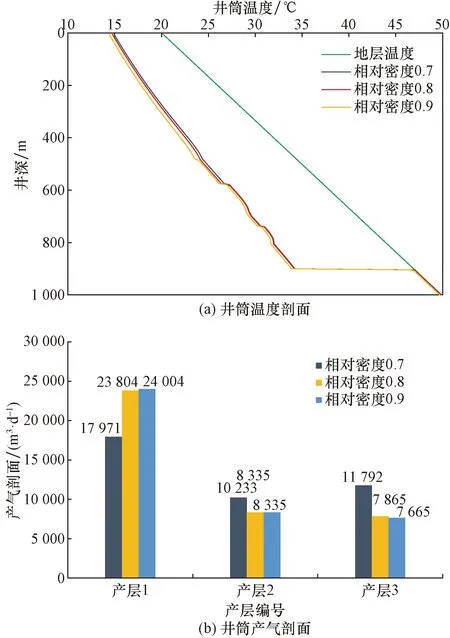
图9 天然气相对密度对井筒温度、产气剖面的影响Fig.9 Influence of natural gas relative density on wellbore temperature and gas production profile

2.2 气藏直定井温度剖面敏感参数分析

从上述单因素分析结果可以看出,气藏直定井温度剖面受不同单因素的影响规律和影响程度各不相同,为了明确影响气藏直定井温度剖面的主控因素,为后续反演解释奠定基础,采用正交试验法对影响油藏直定井温度剖面的不同单因素进行敏感性分析。

根据分析因素设定,选取单井产量(Qg)、渗透率(k)、储层总导热系数(Kt)、储层平均含水饱和度(Sw)、天然气相对密度(dg)、井筒直径(D)及直定井倾斜角(θ)这7个因素,做7因素3水平正交试验分析,各影响因素取值水平设计如表4所示。

表4 正交试验分析因素及水平设计Table 4 Analysis factors and level design of orthogonal test

根据正交试验方案设计,选用L18(37)的标准正交表(表5)进行正交试验分析,以地温剖面与井筒温度剖面之间的平均温度差作为评价指标,用以表征多因素交互影响时,井筒温度剖面的整体变化情况。正交试验结果如表5所示,采用极差分析法,对正交试验结果做敏感性极差分析,结果表明,各个影响因素对气藏直定井温度剖面的影响程度由大到小依次为:渗透率>产量>含水饱和度>井筒倾斜角>天然气相对密度>储层导热系数>井筒半径,即k>Qg>Sw>θ>dg>Kt>D,影响气藏直定井温度剖面的关键参数为渗透率、单井产量和含水饱和度。

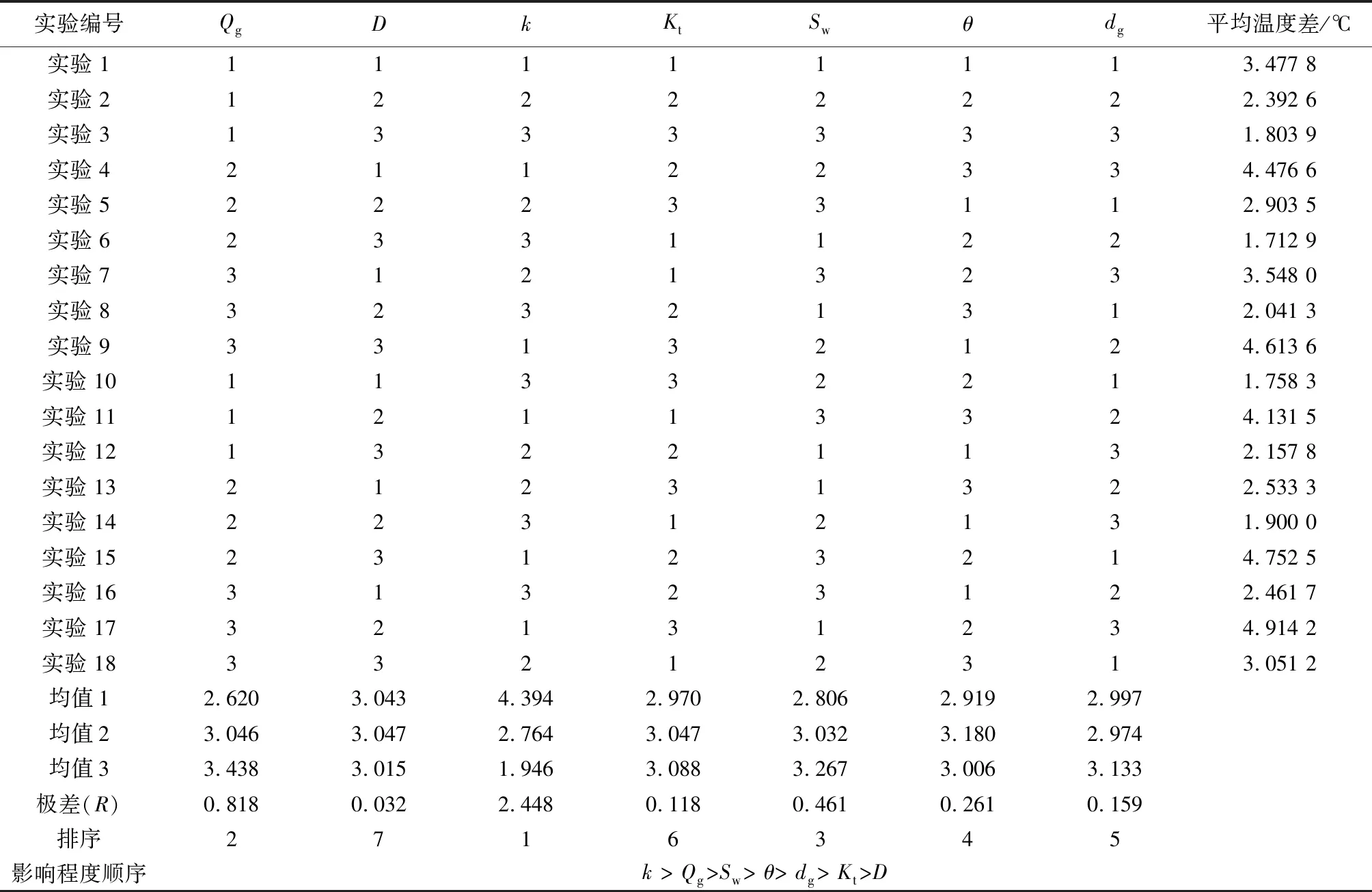
表5 正交试验分析结果Table 5 Analysis results of orthogonal test

因此,在对气藏直定井DTS监测数据进行反演解释时,可以渗透率和含水饱和度分布作为反演目标参数,并以所建立的温度剖面预测模型作为正演模型,模拟退火(simulated annealing,SA)算法[23]、马尔科夫链蒙特卡洛(Markov chain Monte Carlo,MCMC)算法[7]等人工智能算法建立反演模型,即可实现多产层气藏直定井产出剖面定量解释。

3 结论

(1)建立了考虑多种微量热效应的多产层气藏直定井温度剖面预测模型,通过耦合求解,实现了不同单因素条件下气藏直定井的温度剖面模拟预测。

(2)通过温度剖面模拟,分析了不同单因素对气藏直定井温度剖面的影响规律,正交试验分析结果表明各因素对注水井温度剖面的影响程度依次为:渗透率>产量>含水饱和度>井筒倾斜角>天然气相对密度>储层导热系数>井筒半径,影响气藏直定井温度剖面的主控因素为渗透率、产量和含水饱和度。

(3)在对多产层气藏直定井温度剖面监测数据进行反演解释时,可以渗透率、产量和含水饱和度这3个关键特征参数作为反演目标参数进行。研究结果为明确多产层气藏直定井产出剖面以及裂缝参数定量解释奠定了理论基础。