Temperature-induced logical resonance in the Hodgkin-Huxley neuron

Haiyou Deng(邓海游), Rong Gui(桂容), and Yuangen Yao(姚元根)

Department of Physics,College of Science,Huazhong Agricultural University,Wuhan 430070,China

Keywords: stochastic resonance,logical stochastic resonance,Hodgkin-Huxley neuron,temperature

1.Introduction

Numerous studies have demonstrated that noise can play a positive role in nonlinear systems over the past few decades.For instance,noise can be used as an effective method to amplify weak periodic signals.This phenomenon is regarded as stochastic resonance(SR),which was first proposed by Benzi and collaborators when they explored the problem of the periodically recurrent ice ages.[1]In fact, noise can also exert positive effects in the nonlinear systems even if an external weak periodic signal is absent.For example,the noise-driven nonlinear system without an external periodic signal can show resonant oscillation behaviors under moderate noise intensity,thereby significantly improving the regularity of system dynamics, which is called coherent resonance (CR).[2,3]With further research,multiple SRs or CRs have been revealed,and their positive roles in the nonlinear systems have been widely explored and confirmed.[4,5]

Noise widely exists in electronic elements.As described by Moore’s law of miniaturization,further integration density of computer chips causes the aggravation of thermal fluctuations (noise)[6]and noises can seriously impair the performance of the computational devices.[7]Inspired by SR,Murali and collaborators found that noises in computational devices can be exploited constructively to improve the reliability of logical operations.[8]The response of a noise-driven bistable system to two independent aperiodic square waves (considered as two unrelated logic inputs) can be mapped into logic output, where the bistable system can be regarded as a logic gate.An optimal window of noise intensity for bistable system exists, which greatly enhances the success rate of logic operations.[8]This phenomenon is known as logical stochastic resonance(LSR)because of its similarity with SR.[8]LSR can occur even for subthreshold inputs,so it emerges as a potential option for constructing energy-efficient new-fashioned logical devices.Some efforts have been devoted to implementing this new-style LSR-based logical gate.[9-12]In the past decade,LSR has received more and more attention.[13-19]

Noise is not the only factor to induce logical resonance.Periodic force,[20-23]parameter,[24]time delay,[25-27]autapse,[28]coupling,[29,30]and chaotic signal[31,32]can be used as replacements for stochastic noise to obtain similar results with SR.The scope of the research has been extended from typical bistable systems to multi-stable systems in order to explore all types of logical operations.Meanwhile,the constructive role of noise, periodic and chaotic signals in information storage has also been widely investigated by implementing set-reset latch operation.[33-41]Our recent study has verified that the dynamical behaviors of the chaos-driven FitzHugh-Nagumo (FHN) neuron under the periodic forcemodulated input signals can be interpreted as the specific logic output,and the excitable two-state FHN neuron can operate as a logic gate in the optimal range of intensity of chaotic driving force.[42]

Temperature is known to be a pivotal disturbance of biological functionalities in living systems.From the perspective of biochemical reactions, temperature drastically affects enzyme activity,[43]thereby affecting enzyme-catalyzed rates[44]and even the metabolism level of the whole organisms.[45]From the standpoint of information processing and signal transmission,temperature exerts influence on signal propagation through axons by altering the neuroplasticity of the brain and nervous system.[46]Experimental observations show that the opening time of sodium ion channels of the myocardium is influenced by temperature.[47]Furthermore, low temperatures may cause conduction failure of the action potentials,although the action potentials cannot be faithfully conducted either at fever-like temperatures.[48]An optimal temperature exists for the propagation of action potentials.[49-51]In addition, the firing dynamic of the neurons is affected by temperature and the firing frequency is reduced at low temperature.Our recent studies have shown that the successful implementation of logical operation with the FHN neuron is dependent on firing behaviors of the FHN neuron.[42]Thus some interesting issues are naturally aroused: How does the temperature affect logical resonance in the HH neuron? Is there an optimal range of temperature where the HH neuron can work like a specific logic gate?

2.Model and scheme

The temperature-controlled HH neuron model describing the membrane potential of the giant squid axon is given by the following set of equations:[52]

HereVindicates the membrane potential,whilem,nandhindicate the gating probabilities of different ionic channels, respectively.The fixed parameters in equation(1)are presented in Table 1.And the kinetic rates of ion channels are given by[52]

with

The above-mentioned equations (3)-(6) describe that the opening and closing rates of the ion channel at a high temperature are faster than that at a low temperature.The characterIin Eq.(1)stands for external stimuli given by[42]

wheres1ands2are two unrelated aperiodic 2-level square waves.They encode two independent binary logic input signals, respectively, according to the following encoding rule:for logic input 1,s1ands2take value 3.5, or 0 for logic input 0.Bsin(ωt)denotes periodic force with amplitudeBand angular frequencyω,which is used to modulate two input signals.As previously mentioned,[8,15,31]the resting and excited states of the HH neuron are interpreted as logic output 0 and 1, respectively.So the input-output associations for AND &OR logic gates are listed in Table 2.

Table 1.Parameters for the temperaturecontrolled Hodgkin-Huxley neuron model.

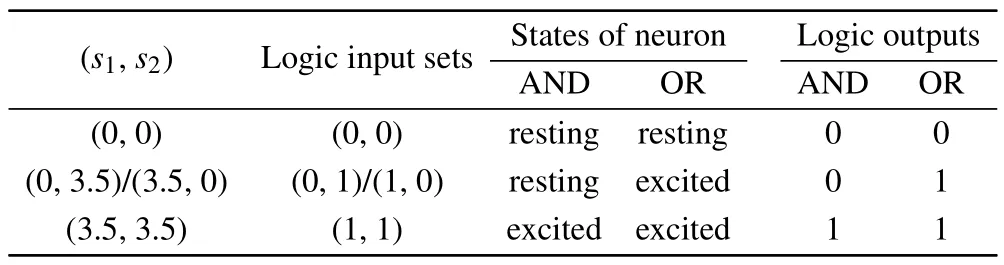
Table 2.The truth table for AND&OR logic operations.

The reliability of the logic gate is very important for logic operations.Here we use the success probabilityPto measure the reliability of the specific logic gate.Pis defined as the ratio of the number of successful runs(n)to the total number of runs (N), i.e.,P=n/N.In a run, for all possible logic input combinations, the logic output obtained is always correct according to the truth table(Table 2),then this run is regarded as a successful one.Because of the delay effect,the input signals1ands2are required to keep unchanged during the time interval (defined as 200 time units), and the unsuccessful logic operation can be tolerated if it occurs during the transient process (defined as the first 10% of this time interval).In addition,the total number of runsNis required to be big enough.In this study,Nis set to 1000.We use the Euler’ algorithm to obtain the dynamics of temperature-controlled HH neuron model,with a fixed time step ∆t=0.001 time units.The initial values are chosen randomly in the reasonable ranges.In fact,control runs with smaller ∆tor greaterNreveal no significant difference in results.

3.Results

As shown in Fig.1,s1ands2are two dependent aperiodic 2-level square waves(Figs.1(a)and 1(b)),and sum ofs1ands2is a aperiodic 3-level square wave (blue line) (Fig.1(c)).According to the encoding rule listed in Table 2,whens1+s2takes value 0 or 3.5, the state of the HH neuron for the AND logic gate is expected to be in the resting state(i.e., the logic output is 0); whens1+s2takes value 7, the state of the HH neuron is expected to be in the excited state(i.e.,the logic output is 1).For low temperature (such asT=6.3◦C), whens1+s2takes value 3.5,the HH neuron lies in the excited state(i.e., the logic output is 1) (Fig.1(c)).In this case, the right AND logic result cannot be obtained.For high temperatures(such asT=18◦C),the HH neuron is not evoked for all possible values ofs1+s2(Fig.1(e)).The desired AND logic result cannot be obtained either.However, for moderate temperature (such asT=10◦C), the consistent AND logic output is always available for all possible values ofs1+s2(i.e.,all possible logic input combinations) (Fig.1(d)).Similarly,appropriate temperature can yield consistent OR logic output(Fig.1(f)), while inappropriate temperature can lead to failure of OR logic operation(Fig.1(g)).Therefore,we conclude that there are optimal ranges of temperature in which the HH neuron operates like a reliable AND/OR logic gate.

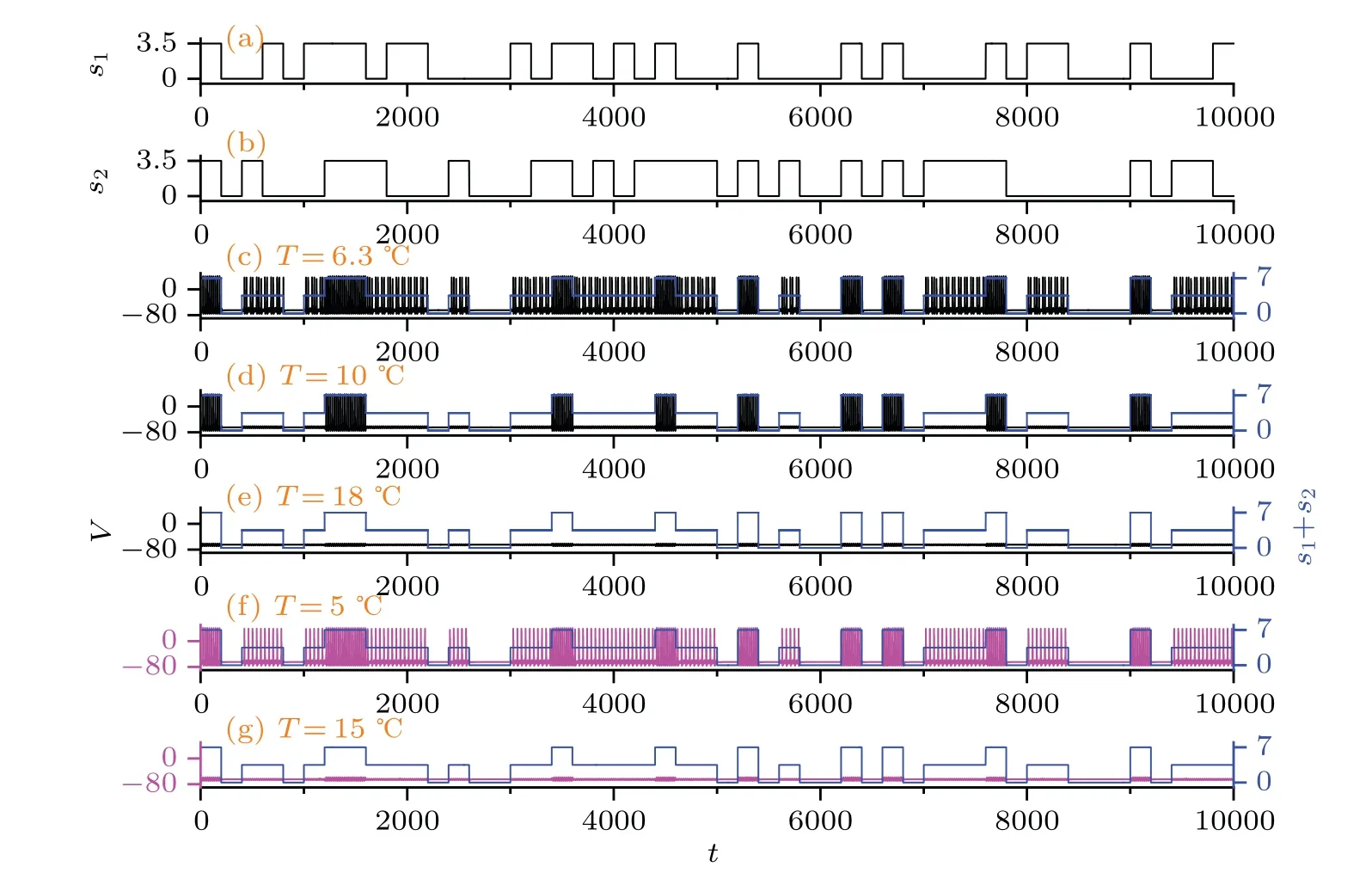
Fig.1.Sampled time series of input signals s1, s2, s1+s2, and membrane potential V of the HH neuron under representative temperatures.Appropriate temperatures can yield consistent(d)AND or(f)OR logic output for all possible logic input combinations. B=0.5,log10(ω)=-0.5.

In order to further obtain the optimal window of temperature, dependence of success probabilityP(AND) andP(OR)on temperatureTare plotted for different amplitudesBof periodic force (Fig.2).It is evident that there are optimal ranges of temperature in which the reliability of AND & OR logic gates can be maximized (Figs.2(a) and 2(b)).Namely,temperature-induced logical resonance phenomenon can occur in the HH neuron model.When frequency is fixed (such as log10(ω)=-0.5), with the increase of amplitudeB, the optimal window of temperature shifts toward higher temperature for the AND & OR logic gates (Figs.3(a) and 3(b)) and gradually broaden for the OR logic gate(Fig.3(b)).Moreover,the position and width of the optimal window of temperature are also affected by the frequency (Figs.4 and 5) when the amplitude is fixed.

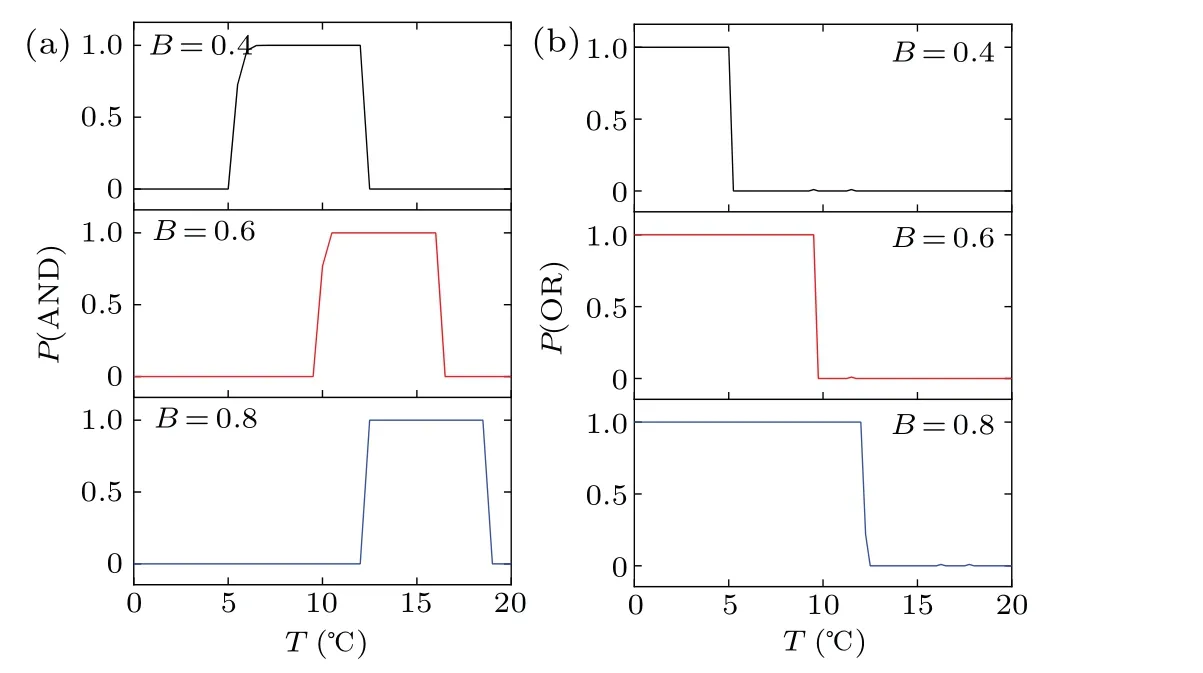
Fig.2.Dependence of (a) P(AND) and (b) P(OR) on temperature T for different amplitudes B.There are the optimal ranges of temperature where success probabilities of obtaining AND&OR logic results are always equal to 1.In other words,temperature-induced logical resonance phenomenon occurs in the HH neuron model.log10(ω)=-0.5.

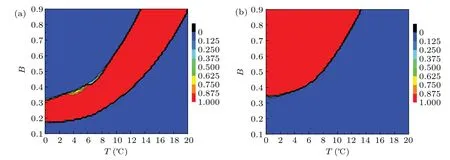
Fig.3.Contour plots of success probability (a) P(AND) and (b) P(OR) in B-T plane.The red region indicates the occurrence of logical resonance.log10(ω)=-0.5.

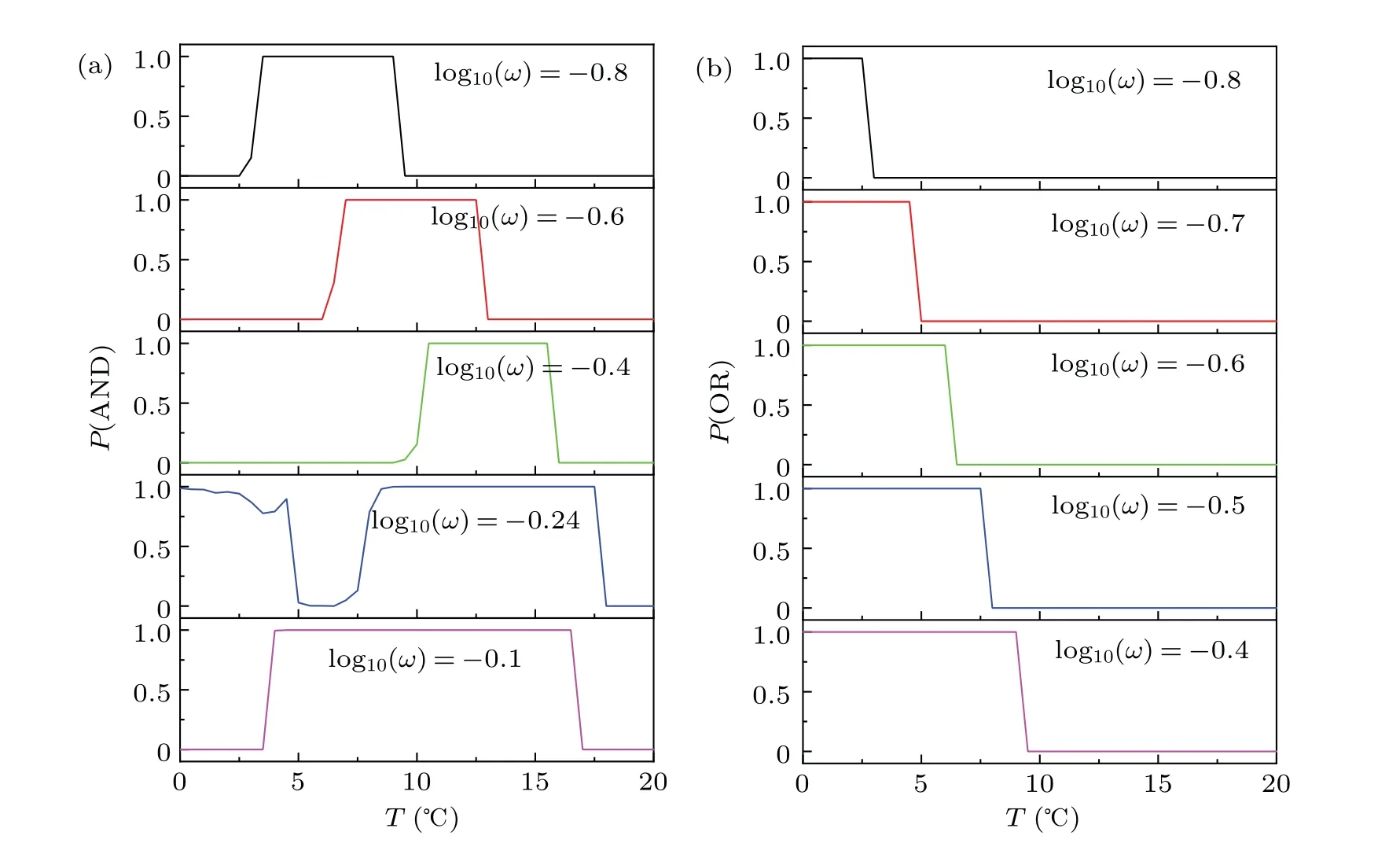
Fig.4.Dependence of (a) P(AND) and (b) P(OR) on temperature T for different frequencies log10(ω).There are the optimal ranges of temperature where success probabilities of obtaining AND & OR logic results are always equal to 1.In other words, temperature-induced logical resonance phenomenon occurs in the HH neuron model. B=0.5.

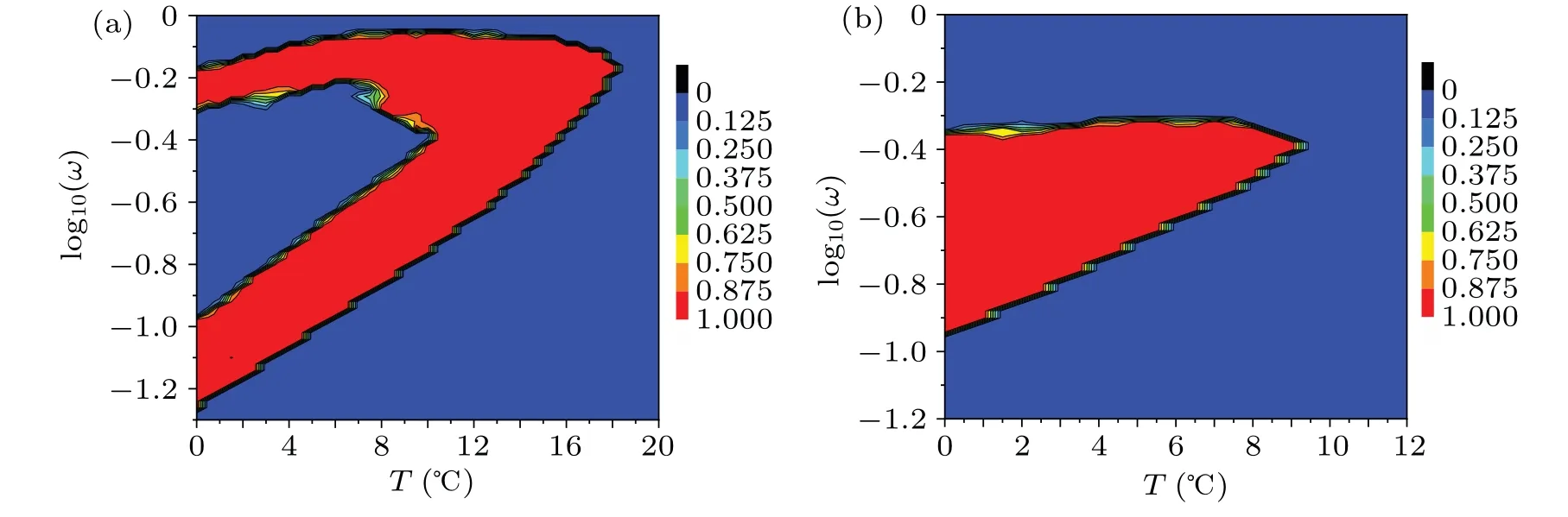
Fig.5.Contour plots of success probability P in log10(ω)-T plane.The red region indicates the occurrence of logical resonance. B=0.5.

Logical resonance can also be obtained in the HH neuron by altering the amplitude or frequency of periodic forceBsin(ωt)if the temperature is appropriate(Figs.3 and 5).Furthermore,the temperature can induce transition of logical resonance (Fig.5(a)).That is to say, the temperature-controlled transition of logical resonance can occur in the HH neuron.For example, the temperature-controlled transition of logical resonance from double to single can be observed clearly with the increase of temperature(Fig.6).

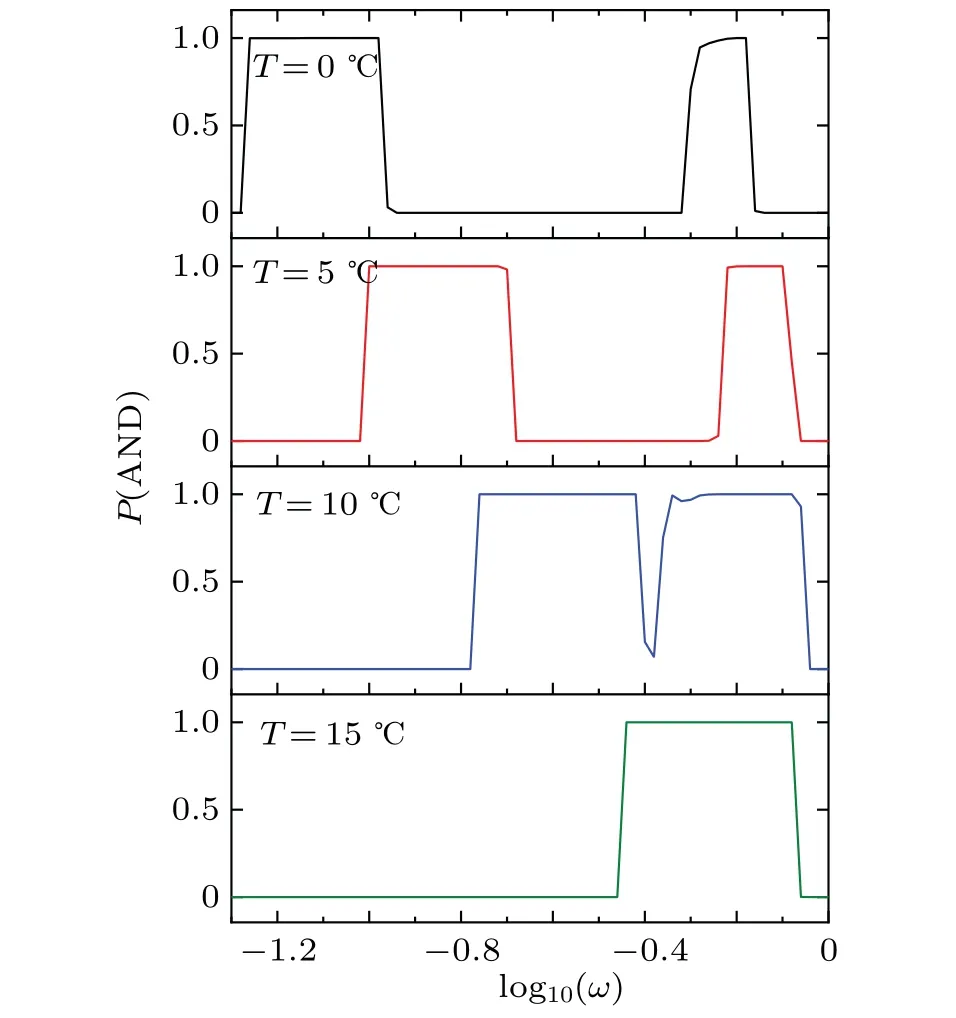
Fig.6.Dependence of P on frequency log10(ω)for different temperatures T for AND logical operation.Clearly,the curves of P versus log10(ω)show resonant behaviors,which indicates the occurrence of logical resonance induced by regulating frequency of periodic force.In addition, from top to bottom,temperature-controlled transition of logical resonance (double-to-single) can be observed clearly with increasing temperature.

Finally,the potential mechanism for temperature-induced logical resonance is given based on phase portrait of the forced temperature-sensitive HH neuron model.Temperature alters the excitability of temperature-sensitive neurons.As illustrated in Fig.7,increasing temperature makes it more difficult for neurons to enter a firing or excitable state.Under low temperature(such asT=6.3◦C),whens1+s2is 0(i.e.,logic input set is(0,0)),external stimuliI(including input signalss1,s2and modulating periodic forceBsin(ωt)) still has enough energy to evoke spikes(Fig.7(a)).So the logic output of the system is 1 in this case.In consequence, the AND logic operation becomes unreliable.But with high temperature (such asT=18◦C), even ifs1+s2is 7 (i.e., logic input set is (1,1)), external stimuliIhas no enough energy to evoke spikes(Fig.7(c))thereby the logic output of the system is always 0.In that case,reliable AND logical operation cannot be implemented.Under an appropriate temperature(Fig.7(b)),the responses of forced temperature-sensitive HH neurons to the input signalss1ands2could always be consistent with the logic input-output associations for specified logic gates.Moreover,the same mechanism can be used to interpret OR logical operation(Figs.7(d)-7(f)).

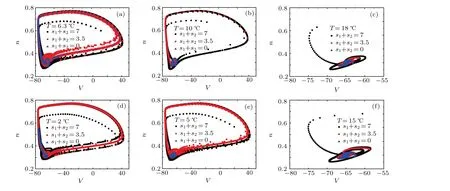
Fig.7.Phase portrait of the forced temperature-sensitive HH neuron model for(a)-(c)AND&(d)-(f)OR logic gates. B=0.5,log10(ω)=-0.5.

4.Conclusions

In this study we attempt to interpret the response of the Hodgkin-Huxley(HH)neuron to external input signals as the desired logic results according to a well-defined rule.We have investigated the role of temperature in the logical resonance of HH neurons.As an indicator of the reliability of the logic gate, the success probabilityPincreases with the increase of temperatureT, reaches the maximum in the optimal window ofT, and eventually decreases, which indicates the existence of temperature-induced logical resonance in the HH neuron.In addition,Palso displays resonant behavior as the frequency or amplitude of the modulating periodic signal increases.That is to say, periodic force-induced logical resonance can happen in the HH neuron.Interestingly, single and double logical resonances can be induced by altering frequency under the proper temperatures.Thus, the transition between single and double logical resonances can be controlled by regulating temperature.Taken together,there is temperature-induced logical resonance and temperature-controlled transition of logical resonance in the Hodgkin-Huxley neuron.These results provide important clues for constructing neuron-based energy-efficient new-fashioned logical devices.

Acknowledgement

This Project supported by the National Natural Science Foundation of China(Grant No.11804111).