Diverse soliton solutions and dynamical analysis of the discrete coupled mKdV equation with 4×4 Lax pair
Xue-Ke Liu(刘雪珂) and Xiao-Yong Wen(闻小永)
School of Applied Science,Beijing Information Science and Technology University,Beijing 100192,China
Keywords: discrete coupled mKdV equation, continuous limit, discrete generalized (r,N-r)-fold Darboux transformation,multi-soliton solutions,rational soliton solutions
1.Introduction
Solitons are a class of nonlinear localized waves with particle-like properties,[1]which have been brought to light in various physical areas, including nonlinear optics, plasma physics, electricity, quantum mechanics, opening up new applications in these fields.[2-5]The history of soliton can be traced back to 1834, the year in which John Scott Russell unexpectedly discovered the phenomenon of solitary wave in a canal.However, it was only with the proposal of the Korteweg-de Vries(KdV)equation from which soliton theory gained massive attention.The most notable feature of solitons is that they can keep the shapes and velocities unaltered while the solitary waves propagate forward.[2]Nonlinear partial differential equations(NPDEs)may model various physical phenomena in optics, biology, plasma, and other research fields.[6-8]However, for some events such as the motion of one-dimensional particles, the propagation of pulses in biological chains and transmission of electrical signals in nonlinear inductance-capacitance circuits,[1,8-11]the discrete nonlinear equations serve as more appropriate descriptions compared with NPDEs.The main motivation for studying the discrete nonlinear equation is that they can keep some characteristics of the original continuous equations unaltered.[12]In Ref.[13],the authors put forward and studied the initial value problem of the followingN-component discrete modified Korteweg-de Vries(mKdV)equation

Equation (3) can yield Eq.(2) by zero-curvature equationAn,t+AnBn-Bn+1An=0.WhenYn=0, Eq.(2) reduces to the single component discrete mKdV equation, whose solitonic interactions and conservation laws of the discrete mKdV equation have been studied in Ref.[16].This equation is also known as the so-called Volterra equation, which may be in connection with the spectrum of Langmuir wave in plasma physics.[1]In Ref.[15],the generalized symmetry and polynomial conserved densities of Eq.(2)have been obtained.Equation(2)can also be turned into the continuous coupled mKdV equation[15]

Some methods for obtaining the exact solutions of discrete integrable equations include the inverse scattering method,[20,21]Riemann-Hilbert method,[22,23]algebraic geometry method,[24]Darboux transformation(DT),[16,25,26]and so on.Among them, the DT is one of the available methods,whose basic idea is to keep the Lax pair of discrete equations covariant.Recently, the discrete generalized (r,N-r)-fold DT technique has been proposed and successfully applied to solve some continuous equations, (2+1)-dimensional equations and discrete equations.[27-29]Generally speaking, the discreteN-fold DT can only obtain solitons,while the discrete generalized(r,N-r)-fold DT can obtain more types of exact solutions, including soliton solutions, rational, semi-rational and their mixed interaction solutions.At present, while the discrete generalized(r,N-r)-fold DT has been primarily utilized for addressing the discrete integrable equations related to 2×2 Lax pair,[11,16,30-32]the research on discrete equations pertaining to 4×4 Lax pair is still rare.[33,34]Therefore, it is significant to extend this method from 2×2 Lax pair to 4×4 Lax pair.To our knowledge, the generalized symmetry and polynomial conserved densities of Eq.(2)have been obtained,whereas there is no relevant research on the higher-order exact solutions like multi-soliton,higher-order semi-rational soliton(SRS), higher-order rational soliton (RS) and mixed interaction soliton solution of Eq.(2).Therefore, in this study, our main interest is to consider multi-soliton and higher-order SRS solutions on the vanishing background, higher-order RS and mixed interaction soliton solutions on the non-vanishing background of Eq.(2) through the discrete generalized (r,N-r)-fold DT.Meanwhile, we perform numerical simulation and asymptotic analysis to analyze the dynamical properties and limit states of some exact solutions.
The rest contents of this paper contain three sections.In Section 2, the continuous limit is used to map Eq.(2) to the coupled KdV equation and a new nonlinear equation without dispersion term.In Section 3, we construct the discrete generalized (r,N-r)-fold DT for Eq.(2), from which the usual multi-soliton,SRS,RS and mixed interaction soliton solutions are given.Moreover,the asymptotic states and numerical simulations of some soliton and rational solutions are also discussed.In Section 4,we give our conclusions.
2.Continuous limit
Continuous limit is a powerful tool to connect the discrete and continuous equations.Due to the fact that the discrete single component mKdV equation can converge to the continuous KdV and mKdV equations under the continuous limit,[35]the discrete coupled mKdV equation(2)may also converge to the continuous coupled KdV and mKdV equations.In Ref.[15],Eq.(2)has been mapped to the coupled mKdV equation(4).In what follows,we will construct the new continuous conditions that make Eq.(2)correspond to two continuous equations.
(i) Equation (2) corresponds to the continuous coupled KdV equation[36,37]
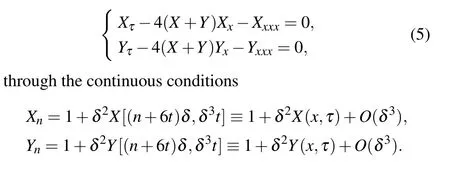
It should be noted that the coefficients of Eq.(5) are different from the coefficients of the coupled KdV equation in Refs.[36,37].In Ref.[36], when selecting special coefficients, Eq.(5) can be derived from a two-layer fluid system.In Ref.[37], the Lax pair of the coupled KdV equation with different coefficients has been constructed via the prolongation structure technique.WhenY=0, Eq.(5)is transformed into the KdV equation,which has been shown to describe the asymptotic development of shallow water waves[38]and ionacoustic waves.[39]
(ii)When taking the limit conditions
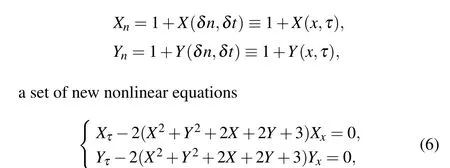
can be obtained.Certainly, Eq.(6) can also reduce to a new single component equation without dispersion term ifY=0.
Therefore, we can conclude that a discrete equation can correspond to different NPDEs under different continuous limits.Equation (6) is a new NPDE without dispersion term,which is worth further research.
3.Discrete generalized(r,N-r)-fold DT
In this section, we will build the discrete generalized(r,N-r)-fold DT for Eq.(2).To begin with, we presume thatΨn(λi) = (Ψ1,n(λi),Ψ2,n(λi),Ψ3,n(λi),Ψ4,n(λi))T(i=1, 2, 3,...,r)arerdifferent fundamental solutions of Eq.(3)based on the initial seed solutionsXnandYn.Then we consider the following gauge transformation:



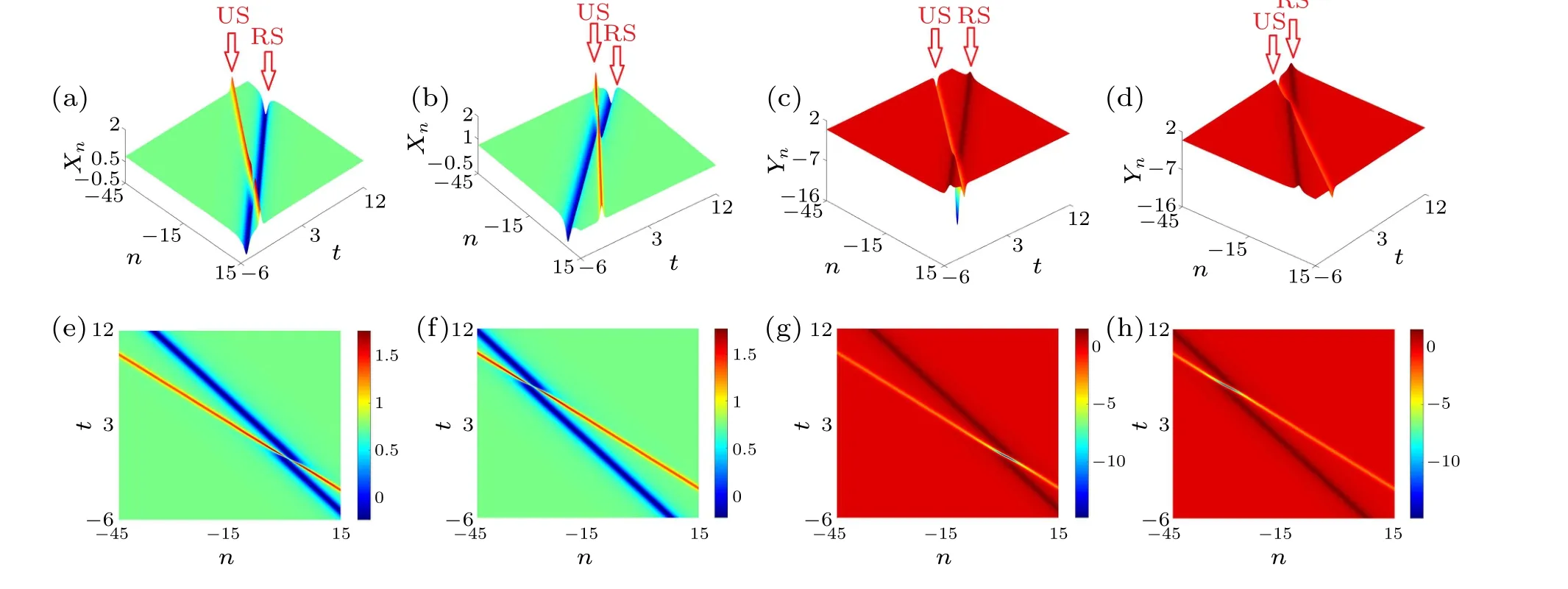
Remark 1 In the above theorem,ris the number of spectral parameterλi,Nis the order number of DT andN-ris the sum of the order number of the highest derivative of the Darboux matrixGnor the vector eigenfunctionΨn.TheN-fold DT can be derived from Theorem 1 by selectingNspectral parameters and without expandingΨninto Taylor series,from which we can obtain the soliton solutions on zero background.Whenr=1,Theorem 1 reduces to the(1,N-1)-fold DT,which can yield higher-order rational and semi-rational solutions on nonzero background.When 1 Based on the zero seed solutionsXn=Yn=0,the fundamental solution of Eq.(2)can be given by Figures 1(a) and 1(c) show the 3D structures of onesoliton solutions ~Xnand ~Yn, while Figs.1(b)and 1(d)display the 2D structures of one-soliton solutions ~Xnand ~Yn, respectively.In addition, in order to analyze the dynamical behaviors of one-soliton solutions,we conduct numerical simulation through the finite difference method,[40]as shown in Fig.2.Figures 2(a),2(e)and 2(b),2(f)are the exact and approximate one-soliton solutions without any noise.Figures 2(c),2(g)and 2(d),2(h)are the perturbed solutions with 2%and 5%noises,respectively.By the numerical simulation,the one-soliton solutions have small fluctuations in a short time when adding 2%noise.As the noise increases,the structures of one-soliton exhibit significant fluctuations. Table 1.Relations between the parameters and shapes of one-soliton solutions.BS:bright soliton;ABS:anti-bell-shaped soliton. Table 2.Physical properties of one-soliton solutions.Energy of ~Xn and~Yn are given by E~Xn=dn and E~Yn= Solitons Amplitude Velocity Wave number Width Primary phase Energy~Xn |(λ41-1)(C2C4-C1C3)|images/BZ_211_579_1225_604_1250.png(C21+C22)(C23+C24) - λ41-1 2λ21 2lnλ1 lnλ1+α (λ41-1)2(C2C4-C1C3)2 2λ21 lnλ1 2lnλ1 1 4λ41(C21+C22)(C23+C24)|lnλ1|~Yn |(λ41-1)(C1C4+C2C3)|images/BZ_211_579_1354_604_1379.png(C21+C22)(C23+C24) - λ41-1 2λ21 2lnλ1 lnλ1+α (λ41-1)2(C1C4+C2C3)2 2λ21 lnλ1 2lnλ1 1 4λ41(C21+C22)(C23+C24)|lnλ1| Fig.1.One-soliton solutions: [(a),(b)]the component ~Xn;[(c),(d)]the component~Yn. Fig.2.One-soliton solutions: [(a),(e)]exact solutions;[(b),(f)]perturbed solutions without noise;[(c),(g)]perturbed solutions with 2%noise;[(d),(h)]perturbed solutions with 5%noise. WhenN=r=2 and Taylor expansions are not performed on spectral parametersλ1andλ2,by choosingC1=C3=-C4=1,C2=1/2 and employing the generalized(2,0)-fold DT,the exact two-soliton solutions are arrived at Table 3.Physical properties of two-soliton solutions. Fig.4.Two-soliton solutions: [(a),(e)]exact solutions;[(b),(f)]perturbed solutions without noise;[(c),(g)]perturbed solutions with 2%noise;[(d),(h)]perturbed solutions with 5%noise. From Eqs.(14), (15) and Table 3, we can conclude that the amplitude and velocity of solitons keep unaltered before and after the collision,but their phases are changed.The twosoliton solutions with spectral parametersλ1=2 andλ2=1/3 are drawn in Fig.3.Figures 3(a), 3(c) and 3(b), 3(d) display the 3D and 2D structures of two-soliton solutions respectively.Figure 4 exhibits the numerical simulation of twosoliton.Specifically, Figs.4(a) and 4(e) are the explicit twosoliton solutions, Figs.4(b) and 4(f) are the perturbed solutions without noise,and Figs.4(c),4(g)and 4(d),4(h)are the solutions with 2% and 5% noises, respectively.From Fig.4,we know easily that the two-soliton solutions can only resist minor noise,but when the noise exceeds 5%,they will exhibit significant fluctuations. WhenN=r=3 and Taylor expansions are not performed on spectral parametersλ1,λ2andλ3, Theorem 1 degenerates into the (3,0)-fold DT, from which we can obtain the three-soliton solutions with the parametersC1=C3=-C4=1,C2=1/2.The structures of three-soliton solutions with spectral parametersλ1=2,λ2=1/3 andλ3=7/3 are displayed in Fig.5.Figures 5(a) and 5(c) display the 3D structures of three-soliton solutions ~Xnand ~Yn.Figures 5(b) and 5(d)show the 2D structures of ~Xnand~Yn,respectively. Fig.5.Three-soliton solutions: [(a),(b)]the component ~Xn;[(c),(d)]the component~Yn. 3.1.2.Higher-order SRS solutions When using the generalized (1,N-1)-fold DT and choosing the parametersC1=C3=-C4=1,C2=1/2, we can obtain some higher-order SRS solutions.Firstly, taking the spectral parameterλ1=2 and expandΨninto the Taylor series withλ=λ1+ε2atε=0: WhenN=2,we can also obtain the second-order SRS solutions by Eq.(8),whose structures are displayed in Fig.7.It should be noted that the second-order SRS solutions includes the exponential and polynomial function, which are different from the two-soliton solutions with only exponential function.From Fig.7,it is obvious that both parameterse0ande1have an impact on the position of the second-order SRS solutions interact. Fig.6.First-order SRS:[(a),(b)]e0=0,[(b),(d)]e0=5. Fig.7.Second-order SRS:[(a),(d)]e0=e1=0;[(b),(e)]e0=3, e1=0;[(c),(f)]e0=0, e1=2. Fig.8.Third-order SRS:[(a),(e)]e0=e1=e2=0;[(b),(f)]e0=2, e1=e2=0;[(c),(g)]e1=3, e0=e2=0;[(b),(f)]e2=5, e0=e1=0. WhenN=3, the structures of the third-order SRS solutions are shown in Fig.8.Similar to the second-order SRS solutions, the third-order SRS solutions also comprises three controlling parameters:e0,e1ande2.These parameters solely govern the position of these SRSs in interaction but they cannot be individually separated. In this subsection, we select the nonzero seed solutionsXn=a,Yn=band substitute them into Eq.(3) to obtain the following fundamental solution: If expandΨnatλ1/=2 into Taylor series, we can also derive the SRS on the non-vanishing background via the discrete generalized(1,N-1)-fold DT.In the following,we will apply the discrete generalized (1,N-1)-fold DT and utilize the above expansions to obtain higher-order RS solutions of Eq.(2). 3.2.1.First-order RS solutions WhenN=1 and employing the generalized (1,0)-fold DT,we can give the first-order RS solutions by Eq.(17),which can be expressed explicitly as Fig.9.First-order RS solutions with e0=0: [(a),(b)]the component ~Xn;[(c),(d)]the component~Yn. The structures of Eq.(20) are shown in Fig.9.Figures 9(a)and 9(c)are the 3D structures of ~Xnand ~Yn, respectively,and Figs.9(b)and 9(d)are the 2D structures of ~Xnand~Yn, respectively.Comparing Figs.2 and 9, there seems to be no difference in appearance between the usual soliton and RS,except for their different seed backgrounds.In fact,there is a notable contrast in the expressions of these two types of solutions.The usual soliton solutions usually contain exponential function or hyperbolic function, while the RS solutions only consist of rational expressions. Like the one-soliton solutions, we perform the numerical simulation on the first-order RS solutions, as shown in Fig.10.Figures 10(a) and 10(e) show the exact first-order RS solutions.Figures 10(b) and 10(f) are the perturbed solutions with no noise.Figures 10(c), 10(g) and 10(d), 10(h)exhibit the solutions with 2% and 10% noises, respectively.From Fig.10,it can be seen that the first-order RS has a small fluctuation when noise is not greater than 2%, whereas the structures of first-order RS may have visible fluctuations if the noise is greater than 2%,such as noise=10%(see Figs.10(d)and 10(h)).Therefore,we can conclude that the first-order RS can resist very small noise. Fig.10.First-order RS solutions with e0=0: [(a),(e)]exact solutions;[(b),(f)]perturbed solutions without noise;[(c),(g)]perturbed solutions with 2%noise;[(d),(h)]perturbed solutions with 10%noise. 3.2.2.Second-order RS solutions WhenN=2 and using the generalized(1,1)-fold DT,we can give the second-order RS solutions by The numerical simulations of solutions(21)are shown in Fig.12.Figures 12(a), 12(e) and 12(b), 12(f) exhibit the exact solutions and perturbed solutions without noises, respectively.They are almost the same.This indicates that our numerical algorithm is correct, in other words, the wave propagations of solutions (21) are stable in the absence of noise.Figures 12(c), 12(g) and Figures 12(d), 12(h) are the numerical structures when adding 2% and 4% noises, respectively.As seen in Fig.12,the structures of solutions(21)have minor fluctuation with the noise not more than 4% in the range oft ∈(-5, 5). Fig.11.Second-order RS solutions: [(a),(c)]e0=e1=0;[(b),(d)]e0=0, e1=2. Fig.12.Second-order RS solutions in Figs.11(a)and 11(c): [(a),(e)]exact solutions;[(b),(f)]perturbed solutions without noise;[(c),(g)]perturbed solutions with 2%noise;[(d),(h)]perturbed solutions with 4%noise. Fig.13.Third-order RS solutions: [(a),(d)]e0=e1=e2=0;[(b),(e)]e0=e2=0, e1=20;[(c),(f)]e0=e1=0, e2=50. 3.2.3.Third-order RS solutions WhenN=3 and using the generalized(1,2)-fold DT,we can obtain the third-order RS solutions, whose structures are shown in Fig.13. Figures 13(a) and 13(d) display the strong interaction of third-order RS solutions.In Figs.13(b) and 13(e), under the effect ofe1,the component ~Xnis shown as three almost parallel RSs in the ranges ofn ∈(-10, 10)andt ∈(-10, 10),where the anti-dark RS appears between two dark RSs.In Fig.13(e),due to the effect ofe1, the component ~Ynis also shown as three almost parallel RSs in the ranges ofn ∈(-10, 10)andt ∈(-10, 10),where the anti-bell shaped RS occurs between two bright RSs.However, they are actually not parallel, and within a certain range,there still exists interaction among three RSs.Figure 13(c) exhibits that the anti-dark RS lies on the right side of two dark RSs,while Fig.13(f)shows that the antibell shaped RS is located on the right side of two bright RSs.However, when the coordinate axis range is large enough,there still exist interactions among these RSs like the secondorder RS. WhenN=r=2 and using the generalized(2,0)-fold DT,we will obtain the mixed solutions of the usual soliton (US)and RS, which are also called the mixed hyperbolic-rational soliton solutions.At this point, we need to use two spectral parametersλ1andλ2.Forλ1, we choose the corresponding parameters asM1=M2=1,M3=-M4=1/ε,a=3/4,λ1=2, while forλ2, we choose the corresponding parameters asM1=M3=-M4=1,M2=1/2,a=3/4,λ2=3.If making Taylor expansion for Eq.(19)atλ=λ1,and without Taylor expansion atλ=λ2, from Eq.(8) we can obtain the mixed hyperbolic-rational solutions as respectively.The structures of solutions(23)are shown in Fig.14. Fig.14.Mixed interaction solutions of US and RS:[(a),(c),(e),(g)]e0=0;[(b),(d),(f),(h)]e0=2. Under the effect ofe0, the position of the first-order RS has shifted, while the US keeps the position unchanged, that is to say,the parametere0can change the interaction position of the US and RS, so we can control the occurrence of the interaction position by changing the parameter. In theory,the discrete generalized(r,N-r)-fold DT can be extended to give more higher-order mixed interaction solutions among US,SRS and RS,but due to the complexity of actual calculations,further study is needed. The discrete coupled mKdV equation (2) with fourthorder Lax pair has been considered systematically,which may describe the motion of shallow water waves, the optical soliton propagation in cubic nonlinear media and the Alfven wave in a cold collision-free plasma.The main innovative results of the present study are as follows: (i) Equation (2) has been mapped to the continuous coupled KdV equation and a new nonlinear equation without dispersion term under the continuous limits. (ii) The discrete generalized (r,N-r)-fold DT of Eq.(2)has been first established, from which diverse exact solutions including the usual multi-soliton, higherorder SRS,higher-order RS and their mixed hyperbolicrational interaction soliton solutions have been given explicitly. (iii) The asymptotic behaviors and related physical quantities of some US and RS solutions have been studied in details. (iv) The dynamical behaviors of some exact soliton solutions are investigated via numerical simulations. We hope the results given in this paper can provide assistance in understanding more physical phenomena in the field of shallow water wave,optics and plasma. Acknowledgments We would like to express our sincere thanks to other members of our discussion group for their valuable comments. Project supported by the National Natural Science Foundation of China (Grant No.12071042) and Beijing Natural Science Foundation(Grant No.1202006).3.1.Multi-soliton and higher-order SRS solutions on the vanishing background














3.2.Higher-order RS solutions on the non-vanishing background










3.3.Mixed hyperbolic-rational soliton solutions on nonvanishing background
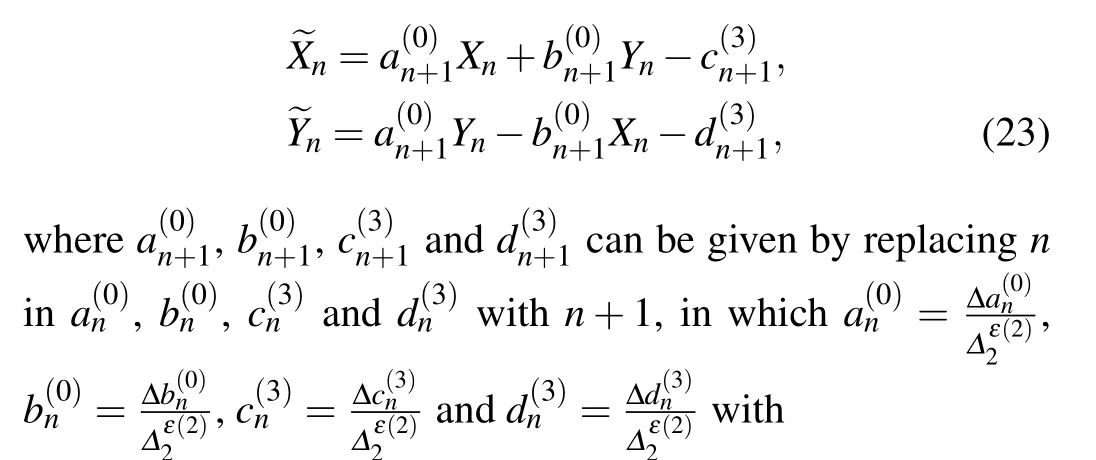

4.Conclusions
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Multi-channel generation of vortex beams with controllable polarization states and orbital angular momentum
- Calibration of quantitative rescattering model for simulating vortex high-order harmonic generation driven by Laguerre-Gaussian beam with nonzero orbital angular momentum
- Materials and device engineering to achieve high-performance quantum dots light emitting diodes for display applications
- From breather solutions to lump solutions:A construction method for the Zakharov equation
- Complete population transfer between next-adjacent energy levels of a transmon qudit

