Mixed-field effect at the hyperfine level of 127I79Br in its rovibronic ground state: Toward field manipulation of cold molecules

Zhengbin Bao(包正斌), Defu Wang(王得富), Xuping Shao(邵旭萍),

Yunxia Huang(黄云霞), and Xiaohua Yang(杨晓华)‡

School of Science,Nantong University,Nantong 226019,China

Keywords: hyperfine structure,mixed Zeeman and Stark effect,evaporative cooling,IBr molecule

1.Introduction

The development of cold molecular physics[1-5]in recent years enables the experimental precise investigation of the molecular hyperfine structure together with its field effect.In return,the well-determined molecular hyperfine structure and its field effect will undoubtedly help to further cool cold(mK)molecules into the ultracold(µK)regime via laser/microwave and magnetic/electric field control.Therefore, the field effect of the molecular hyperfine structure is essential in cold physics.

Polar (heteroatomic) bi-alkali molecules[6-11]are the most intensively studied species, which are produced via the laser-cooled atomic association method, and cold KRb molecules have been cooled to the Fermi degeneracy regime.[6]However, polar alkali molecules suffer from the chemical reaction, which shortens the lifetime of the cold molecules, resulting in limiting applications of cold polar alkali molecules, even though an applied electric field can partly suppress such chemical reactions.[12]Contrarily,heterohalogen diatomic molecules are chemically stable and will probably have wider applications in the field of cold physics.In addition,they would probably be Stark decelerated into the equivalent temperature of 1 mK by employing the near-reddetune laser assisted Stark deceleration scheme.[13-15]

The manipulation of cold molecules via mixed magnetic and electric fields offers three degrees of freedom to tune,two magnitudes of the two fields,and the angle between them,and thus, the mixed field manipulation should be more powerful.The pure Zeeman or Stark effect of the IBr molecule at the hyperfine level has been studied previously.[16]The mixed-field effect is studied in the present work.The rovibronic ground state of the IBr molecule is of1Σ symmetry, so the state has neither a Zeeman nor Stark effect at the rotational level,while it has both Zeeman and Stark effects at the hyperfine level.The field effect at the hyperfine level is about one-thousandth(10-3) weaker[17]than that at the rotational level; therefore,cold polar halogen molecules can be finely controlled by applied fields.

2.Theory

The hyperfine state of diatomic molecules can be represented on the basis of either total angular momentum and nuclear spins coupled or uncoupled.In the coupled basis, the molecular total angular moment excluding nuclear spinJfirst couples with the larger nuclear spinI1to form the intermediate momentG, thenGcouples with the smaller nuclear spinI2to form total angular momentF,andMFis the projection quantum number ofFalong a laboratory frameZ-axis; thus,the state is represented as|JI1GI2FMF〉.The image of the physics of the coupled basis is much clearer and the nuclear spin interaction is nearly treated as a perturbation.However,a strong applied external field may cause decoupling of the angular momenta, which may result in larger errors.In the uncoupled basis, the state is represented as|JMJI1M1I2M2〉,

whereMJ,M1,andM2are projection quantum numbers ofJ,I1, andI2, respectively.However,MJ,M1, andM2are not good quantum numbers in the weak field limit.In the present work,we compute the mixed field effect in the uncoupled basis because of the simple form of the program and label the quantum states in the coupled one due to its clear image of physics,whereG=MJ+M1andMF=MJ+M1+M2.

When we study the hyperfine state of the rovibronic ground state, the Hamiltonian of electronic and vibrational terms is set to be 0.The rotational term of a diatomic molecule is

whereB0is the rotational constant andD0is its centrifugal distortion constant.

The hyperfine structure consists of two parts.The nuclear quadrupole interaction with the gradient of the electric field at the nuclei caused by the surrounding electrons is[18,19]

whereeQqis the nuclear quadrupole constant, andkdenotes the two atoms forming the molecule.And the nuclear spin interaction with the molecular rotational magnetic field is

whereCkis the nuclear spin-rotation coupling constant.The nuclear spin-spin interaction is much weaker[16,20,21]and thus neglected.

The Hamiltonian matrices are, on the uncoupled basis,expressed as[22]

wherepis used to label the space-fixed components,()is the Wigner 3-jsymbol,andC2for IBr is too small to be neglected.

The Stark effect describes the interaction of the molecular electric dipole(µ)with the applied electric field(E)along the laboratoryZ-axis,

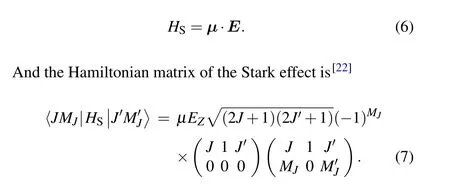
The Zeeman effect describes the interaction of the molecular magnetic dipole interaction with the applied magnetic field along the laboratoryZ-axis

wheregrandgkare the rotational and nuclear Land´eg-factor,respectively,µNis the nuclear magneton,andσkis the shielding coefficient of the atomic electrons to the nuclear spin.The Hamiltonian is diagonal in the uncoupled basis and is expressed as[23]

When the electric field is parallel to the magnetic fields, the mixed-field effect of the hyperfine structure is merely the sum of the two individual field effects.However,when the included angle between the electric field and the magnetic field isβ,the anisotropy Stark effect in the new coordinate(Z′-axis)should be rotated to the magnetic-field-fixed coordinate(Z-axis)and is rewritten as[24]

3.Results and discussion

We study the mixed electric and magnetic field effect of the hyperfine levels in the rovibronic ground state of IBr under the condition of the magnetic field ranging from 0 to 1000 G and the electric field ranging from 0 to 1000 V·cm-1.The molecular constants of IBr adopted in the present work are listed in Table 1 of Ref.[16].The computation program is modified based on that of Ref.[26].

Figure 1 plots the mixed electric and magnetic fields effect of the hyperfine levels in the rovibronic ground state of IBr varying with the electric field ranging from 0 to 1000 V·cm-1at a parallel fixed magnetic field of 1000 G.The Stark sublevels with oppositeMFare degenerate at a pure electric field.However, they become nondegenerate at mixed electric and magnetic fields,and thus,the hyperfine levels of the rovibronic ground state of IBr split into 24 sublevels,as shown in Fig.1.The sublevels are complicated and congested, and they cross or avoidcross each other.To show such complex crossing or avoid-crossing phenomenon clearly, the states are plotted in individual figures as follows.Note that the energy of the rovibronic ground state (neglecting the hyperfine structure) is set to be 0.

Fig.1.The hyperfine levels of the rovibronic ground state of IBr (X1Σ,v=0, J =0) varying with the applied electric field at a parallel fixed magnetic field of 1000 G.The energy of the rovibronic ground state(neglecting the hyperfine splitting)is set to be 0.

Figure 2 plots the mixed-field effect of the|F,MF〉 =|4,MF〉 sublevels varying with the magnetic field at a fixed electric field (as labeled) and at different angles ofβ(as labeled) of the two fields.Figure 2(a) shows that, besides those level direct crossings,the|4,-2〉(black)sublevel avoids crossing with the|4,-3〉(red)at the magnetic field of around 750 G.The avoid-crossing behavior is caused by the perturbation due to that, the applied magnetic field couples those sublevels with the same odd/even parity while the electric field couples those opposite parity ones.The avoid-crossing is rare and can only be observed at relatively large electric and magnetic fields when the two fields are parallel, as shown in Fig.2(a).If we rotate the angle between the two fields,however, the avoid-crossing changes significantly to the applied magnetic field, as shown in Figs.2(b)-2(d).Therefore, it is possible to bring sublevels of the opposite parity into degeneracy by either varying the applied electric and/or magnetic fields or rotating the angleβbetween them.Figure 2(d)shows the mixed-field effect varying with the magnetic field ranging from 0 to 1000 G at the electric field of 1000 V·cm-1and the 30◦angle of the two fields, and figures 2(e) and 2(f) show the details of the shadowed part in Fig.2(d).The|4, -4.〉sublevel does cross with the|4,2〉 (no perturbation happens),while the|4,-3〉avoid-crosses with the|4,-4〉(perturbation takes place) around the magnetic field of 540 G, as shown in Fig.2(e).Figures 2(b) and 2(c) show such mixed-field effect at 45◦and 90◦angles of the two fields, respectively.It can be concluded that the angle between the two fields does not change the pattern so much but changes the crossing and avoid-crossing points along the magnetic axis.For example,the above mentioned avoid-crossing point of the|4,-3〉 and|4,-4〉sublevels varies with the angle: around 540 G at 30◦,around 610 G at 45◦,and around 560 G at 60◦(not plotted in Fig.2).Additionally,the perturbation strength decreases with the increasing of the angle, which can be deduced from the separation of the two perturbed sublevels at the avoid-crossing point,and the perturbation nearly vanishes at 90◦as shown in Fig.2(c).Hence,the molecular mixed-field effect can be tuned by varying the strength of the applied two fields and/or rotating the angle between them,that is,three degrees of freedom can be utilized to tune for applications.

As shown in Fig.2(d), the|4,-3〉 (red) sublevel Feshbach likely resonates with the applied magnetic field at a fixed electric field whenβ=30◦due to perturbations.It is weak-field seeking in the weak magnetic field regime, but it transits into strong-field seeking around the magnetic field of 315 G due to its perturbation with the|4,-2〉 (black) until it re-transits into weak-field seeking around 540 G due to its perturbation with the|4,-4〉 (green), and finally such transitions may happen repeatedly due to its perturbations with the|4,-2〉 and other possible sublevels.Therefore, by applying an assisted DC electric field at a certain angleβand tuning the magnetic field adiabatically, the molecules are possibly converted between the magnetic weak-field-seeking state and the strong-field-seeking state.This corresponds to changing the orientation of the molecular magnetic moment with respect to the magnetic field axis.[27]Such reorientation may modify the mechanisms of inelastic scattering and chemical reactions at low temperatures and result in enhancement or suppression of collision rates.[28-31]This Feshbach-like resonance may also have other potential applications.[32,33]

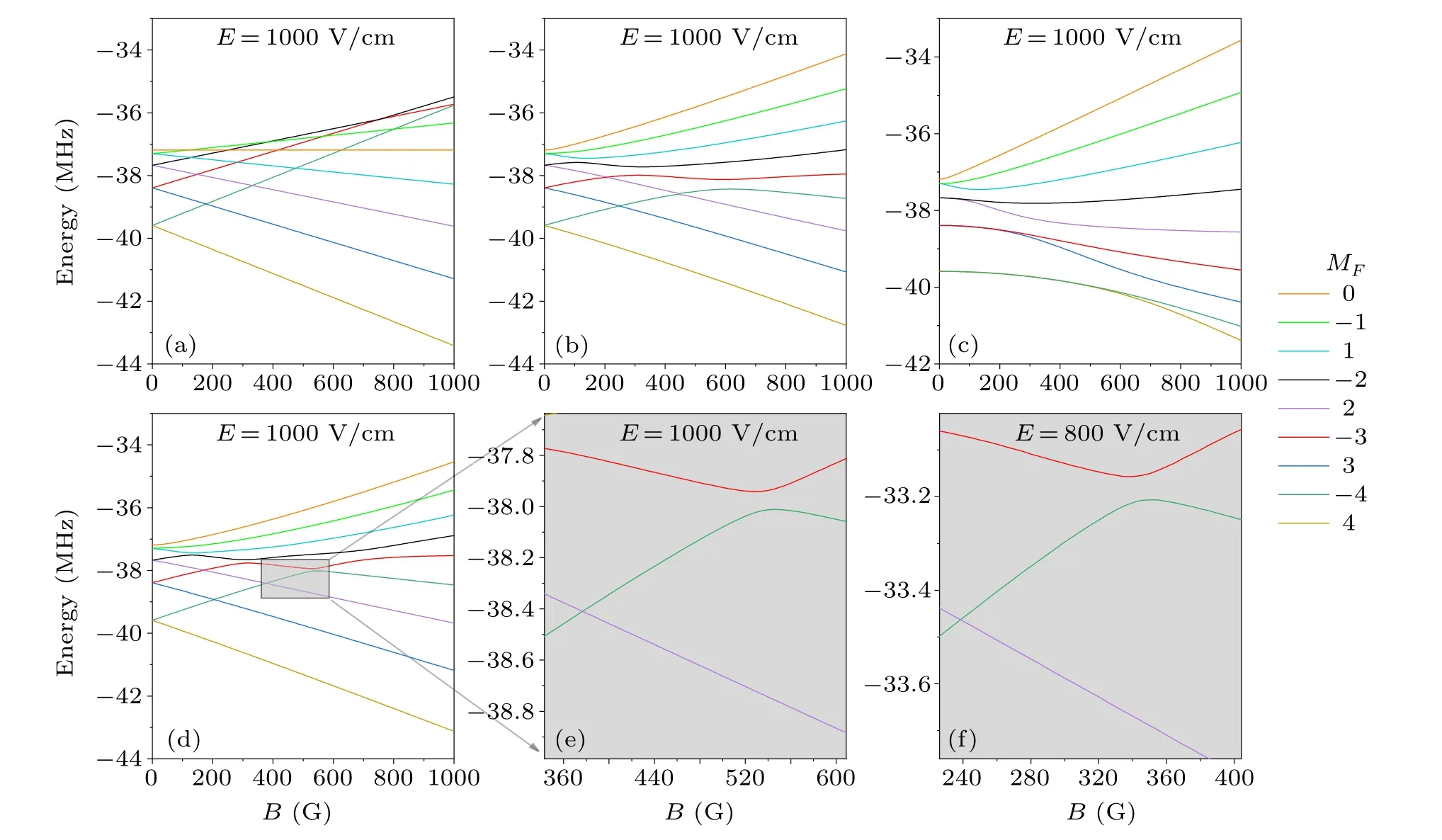
Fig.2.The|F =4,MF〉hyperfine sublevels of the rovibronic ground state of IBr varying with the applied magnetic field and fixed electric field at different angles.Panel (a) plots those at the angle between the applied magnetic field and electric field β =0◦at the fixed electric field of E=1000 V·cm-1;(b)β =45◦,E=1000 V·cm-1;(c)β =90◦,E=1000 V·cm-1;(d)β =30◦,E=1000 V·cm-1.Panel(e)shows the insights of the shadowed part of(d);and(f)is similar to(e)only the fixed electric field decreased to be 800 V·cm-1.

Another potential application is to trap cold molecules in an electric-field-assisted anti-Helmholtz magnetic trap and implement evaporative cooling by tuning the electric field strength, as illustrated in Fig.3.Molecules may be prepared in the|4,-4〉(green in Fig.2)sublevel[16,34]and be trapped in such trap.As shown in Figs.2(e)and 2(f),the avoid-crossing point may be tuned along the magnetic axis by varying the magnitude of the applied electric field at a 30◦angle about the magnetic field.The avoid-crossing point changes from 540 G to 345 G when the electric field decreases from 1000 V·cm-1to 800 V·cm-1, resulting in the depth of the trap decreasing accordingly.Therefore, the electric field acts as a knife to cut the wall of the trap and molecular evaporative cooling can be achieved in such a trap.Furthermore, the depth of the trap can be rapidly tuned to match the re-thermalization time (typically at the order of several milliseconds) via tuning the strength of the assisted electric field, but the depth of a pure anti-Helmholtz magnetic trap can hardly be tuned so rapidly.In addition, if we evaporatively cool cold molecules by lowering the magnetic field strength in a pure magnetic field trap, the trap will become incompact, and thus, results in a lower density of the achieved cold molecules.The present proposed electric-field-assisted magnetic trap differs from that of Ref.[35], in which the electric field firstly helped load the slowed molecules into the magnetic trap,then provided a perturbation at a fixed applied electric field, and finally, another microwave field was utilized to act as the knife to implement the evaporative cooling.As shown in Fig.3, the assisted electric field of 1100 V·cm-1, 900 V·cm-1, 700 V·cm-1,500 V·cm-1, and 300 V·cm-1corresponds to the trap depth of about 92 µK, 61 µK, 37 µK, 19 µK, and 7 µK respectively, when we trap IBr molecules in the|4,-4〉 sublevel in their rovibronic ground state with the 30◦angle between the two fields.Consequently,IBr molecules might be cooled from 100µK into the severalµK regime via evaporative cooling in such electric-field-assisted anti-Helmholtz magnetic trap.For favorable molecules, it might be employed to cool molecules from several mK into the sub-µK regime.

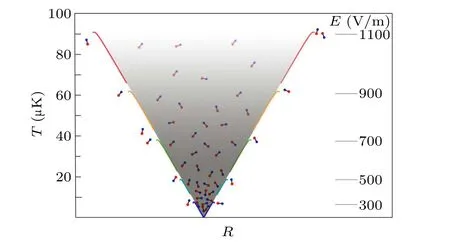
Fig.3.The schematic diagram of an electric-field-assisted anti-Helmholtz magnetic trap for cold molecular evaporative cooling.The electric field acts as a knife to cut the wall of the magnetic trap and thus changes the depth of the trap.Therefore, such molecular cooling can be realized by decreasing the electric field.As to the |F =4, MF =-4〉 level of the|J =0, v=0〉 state in the X1Σ of IBr, the trap depths are about 92 µK,61 µK, 37 µK, 19 µK, and 7 µK at the electric fields of 1100 V·cm-1,900 V·cm-1,700 V·cm-1,500 V·cm-1,and 300 V·cm-1,respectively.

Fig.4.The |F =1, MF〉 hyperfine sublevels of the rovibronic ground state of IBr varying with the magnetic field and a fixed electric field of E=1000 V·cm-1 at different angles of the two fields.(a)β =0,(b)β =30◦,(c)β =45◦,(d)β =60◦,(e)β =75◦,and(f)β =90◦.

Fig.5.The|F =2,MF〉and|F =3,MF〉hyperfine sublevels of the rovibronic ground state of IBr varying with the magnetic field and a fixed electric field of E=1000 V·cm-1 at different angles of the two fields.(a)β =0,(b)β =30◦,(c)β =45◦,(d)β =90◦.

Figure 4 plots the|1,MF〉sublevels varying with the magnetic field ranging from 0 to 1000 G at a fixed electric field of 1000 V·cm-1at differentβangles.The|1,0〉 sublevel is normally diamagnetic and the|1,±1〉 sublevels are linearly paramagnetic but insensitive to the magnetic field for the|dE/dB|< 694 Hz·G-1when the two fields are parallel as shown in Fig.4(a).When the angle between the two fields is rotated,as shown in Figs.4(b)-4(f),the|1,0〉sublevel becomes slightly nonlinearly paramagnetic, and the|1,±1〉sublevels become nonlinearly paramagnetic and more insensitive due to perturbation.Such behavior of the hyperfine states of theF=1 sublevels of the rovibronic ground state IBr molecule in the mixed electric and magnetic fields might have some potential applications in cold molecular manipulations and collisions.

Figure 5 plots the|2,MF〉 and|3,MF〉 sublevels varying with the magnetic field ranging from 0 to 1000 G at a fixed electric field of 1000 V·cm-1at differentβangles.The behaviors are similar to those of the|4,MF〉 described above.If rovibronic ground state IBr molecules are trapped in the|3,-3〉 (red) sublevel in the above proposed electric-fieldassisted anti-Helmholtz magnetic trap,the trap depth is a little bit shallower than that in the|4,-4〉.Figure 6 plots the mixed field effect varying with the angle ranging from 0◦to 90◦at both a fixed magnetic field of 1000 G and an electric field of 1000 V·cm-1, and it is symmetrical about the 90◦axis.It clearly shows that the perturbation can be tuned by only rotating the angles while keeping the fields unchanged.

As described in Section 2,the above results are obtained on the uncoupled basis, which may cause some errors in the weak field region.When the field shift of the sublevel is much less than the hyperfine splitting, it can be treated in the weak field(J-Icoupled)limit.When the field shift of the sublevel,however, is comparable with, and even larger than, the hyperfine splitting,the weak field limit does not work anymore.Therefore,to check the validity of our results,we compare the pure Zeeman or Stark effect obtained on the coupled and uncoupled basis.We found that the errors of the two methods are about 2%in our computed-field range,and a 200 G magnetic or 350 V·cm-1electric field begins to cause the decoupling ofJ-I.The error only shifts the avoid-crossing a little,and thus,it does not affect the applications discussed above.

Fig.6.The hyperfine sublevels of the rovibronic ground state of IBr varying with the angle of the magnetic and electric fields at fixed fields of B=1000 G and E =1000 V·cm-1.The behavior of the sublevels is symmetric about the 90◦-axis.

4.Conclusion

The mixed electric and magnetic fields effect of IBr at the hyperfine level in its rovibronic ground state is computed on the basis of the uncoupled basis of|JMJI1M1I2M2〉 while the sublevels are labeled at the coupled basis of|JI1GI2FMF〉,and the computer program is modified based on that of Ref.[26].The perturbations are insensitive to the applied magnetic field and only one perturbation is observed at relatively large fields when the two fields are parallel.However, the perturbations increase significantly and the Feshbach-like resonance phenomenon is observed when the angle of the two fields is tuned off-parallel.The molecular behavior at the hyperfine level in the mixed electric and magnetic fields can be utilized to control cold molecular collision and chemical reactions, to enhance or suppress the collision and reaction rates.Such behavior may also be utilized to manipulate cold molecules and even to further cool molecules from sub-mK into the µK regime by an evaporative cooling method in an electric-field-assisted anti-Helmholtz magnetic trap.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant No.12004199).