基于李雅普诺夫指数的混沌行为分析

安鸿宇 王云翔 周迪克

摘 要：文章探讨了在新冠肺炎疫情前后，云南板块指数系统动态特性的变化，并且通过计算混沌度量化云南板块指数系统的混沌性质。结果显示，新冠肺炎疫情前后，云南板块指数系统的混沌度发生了显著变化。不仅最大李雅普诺夫指数增加，极差也呈上升趋势，这表明系统的动态性和不稳定性有所增强，整体上系统的混沌度有所提高，反映了系统在特殊时期冲击下的复杂响应。这一研究不仅有助于深入理解云南板块市场的行为特征，还为金融市场风险调控提供了新的视角和方法。此结果为构建混沌时间序列模型和探索系统的非线性特性提供了支持，有助于更好地应对金融市场的变化与挑战。

关键词：混沌时间序列；李雅普诺夫指数；混沌度；云南板块

中图分类号：F830.9文献标识码：A文章编号：1005-6432（2023）36-0042-04

DOI：10.13939/j.cnki.zgsc.2023.36.042

1 引言

在新冠肺炎疫情的背景下，云南板块指数凸显出其作为评估云南上市企业表现的重要尺度。这一指数不仅展现了云南企业在市场上的价值和引导作用，更在特殊时期彰显了其特殊意义。在这充满不确定性的大背景下，云南板块指数突显了其代表云南上市企业的关键地位。

然而，仅仅基于线性时间序列来研究股指波动性，难以充分考量系统本身的不规则性和复杂性[1]。为了更全面地揭示这些方面，提出了利用混沌系统的混沌度来解释云南板块指数系统的不规则性和复杂性。

2 混沌检验方法

现有的研究文献在研究股票市场中是否存在非线性和混沌行为所获得的结果主要取决于每项研究中使用的数据和方法。在检验方法上，现有文献中存在大量检验方法来检验金融市场的混沌信号，如White 检验、Teraesvirta 检验、Keenan 检验、Tsay 检验、Engle LM 检验、BDS 检验、李雅普诺夫指数和 0-1 检验。从技术上讲，李雅普诺夫指数被认为是唯一明确设计用于检验混沌信号，并测量系统信息丢失速率的一种方法，学者对李雅普诺夫指数检验的研究也是较为丰富的[2-3]。相比于传统的李雅普诺夫指数，也有学者用李雅普诺夫指数的衍生方法做过混沌信号检验[4]。

可以看出现有文献主要集中在对各国大盘或特定行业的金融市场进行混沌信号研究。少数文献关注了地方板块的金融混沌信号，其中以云南板块为例。云南板块作为一个代表性地方性市场，在全球经济变动和新冠肺炎疫情冲击下的混沌信号研究相对较少。因此，对于地方性市场的金融混沌信号研究具有重要意义。

文章旨在填补这一研究空白，将焦点聚焦在云南板块的金融混沌信号上。为了深入了解云南板块市场的波动性和复杂性，采用李雅普诺夫指数来进行混沌信号检验。

3 相空间重构

相空间重构可以将云南板块指数转化为一个多维空间，帮助更好地理解云南板块系统的动态行为。相空间重构技术有两个关键参数：嵌入维数 m和延迟时间 τ。其核心思想是通过观测值构建出一组m维向量：

y（t）=［xt，xt+τ，xt+2τ，…，xt+（m-1）τ］∈Rm

按照 Takens 定理就可以恢复其动力学特性。因此需要寻找一个合适的嵌入维数 m，使得 m≥2d+1（d是動力系统维数），以及一个延迟时间使得原系统经过时间延迟后可以作为独立的坐标来使用。

本研究所选用的数据范围为自 2016 年 1 月 19 日至 2023 年 7 月 31 日，采集自东方财富网的云南板块指数的日交易数据。针对新冠肺炎疫情这一时间节点，将数据序列分割成两个子序列：其一为 2016 年 1 月 19 日至 2019 年 11 月 29 日，即特殊时期前；其二为 2019 年 12 月 2 日至 2023 年 7 月 31 日，即特殊时期后。

3.1 虚假临近点法计算嵌入维数

将一维空间的云南板块指数序列逐渐恢复到高维空间中，一维空间上有的时候相邻的两点也会被分离，这两个在一维空间相邻的点也就是虚假邻近点。虚假邻近点法的核心就是随着嵌入维数的增大，混沌运动的轨道会被打开，伪邻近点就会被逐渐剔除，从而整个混沌运动的轨迹得到恢复。对于 m维相空间的向量 y（t）存在 yNN（t）使得有一个欧几里德距离的最邻近点距离是：

Rm（t）=︳︳y（t）-yNN（t）︳︳

然后增加空间的维数为 m+1， 新的欧几里德距离则变为 Rm+1（t）。令

ρ（t，m）=︳︳y（t+mτ）-yNN（t+mτ）︳︳Rm（t）

如果

ρ（t，m）＞Rτ（Rτ∈［10，50］）

那么 yNN（t）就是 y（t）的虚假邻近点。对于云南板块指数序列，计算中从嵌入维数的最小值 2 开始，计算虚假邻近点的比例，然后逐渐增加维数直到虚假邻近点的比例小于 5% 或者虚假邻近点数量不再随着维数的增加而减少时，可以认为混沌吸引子已经完全打开，此时的维数就是嵌入维数。

特殊时期前后的云南板块指数的嵌入维数从 2 开始增加到 3 为一个顶峰，此时的维数为最佳嵌入维数3。

3.2 自相关系数法计算延迟时间

自相关系数可以用以下公式表示：

r（τ）=∑nt=τ+1（xt-x—）（xt-1-x—）∑nt=1（xt-x—）2

其中，r（τ）是延迟时间为 τ 时的自相关系数；x—是时间序列数据的平均值；n是时间序列数据的总长度。

通过计算可得，新冠肺炎疫情前延迟时间 τ为 2，特殊时期后延迟时间τ为 1。

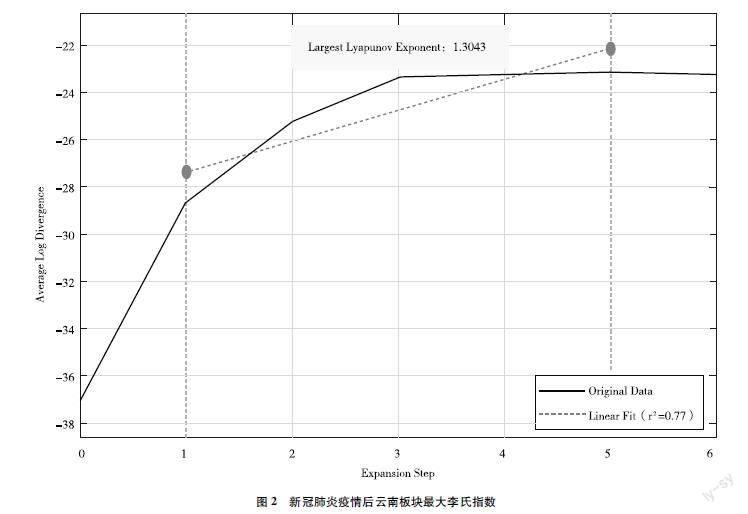
4 最大李雅普诺夫指数

最大李雅普诺夫指数是用于衡量动态系统的混沌特性的一个关键指标。它通过测量在相空间中相邻轨迹的指数分离率来判断系统是否呈现出混沌行为。令最大李雅普诺夫指数为 λ，且

λ=limΔt→∞limΔx（0）→01ΔtlnΔx（Δt）Δx（0）

当 Δt趋近于无穷大时，表示系统在相空间中的轨迹已经发生了足够的演化。Δx（0）是初始状态下的微小差异，它在相空间中定义了轨迹之间的初始距离。Δx（Δt）是时间间隔Δt后，初始状态下微小差异的演化距离。

由结果可知，特殊时期前后的云南板块指数的最大李雅普诺夫指数均大于 0。结果还表明，在特殊时期之前和之后，云南板块的李雅普诺夫指数均呈现出大于 0 的趋势，说明随着时间推移，云南板块按指数形式分离。表明云南板块指数系统的高度敏感性和不可预测性。特殊时期可能对经济、社會以及其他影响因素造成剧烈的影响，导致系统中微小变化的非线性扩散，进而引发了混沌行为。

5 混沌度

设向量：

α=（λ，d，g）

表示云南板块系统的混沌度向量，其中， λ为该系统的最大李雅普诺夫指数，d为系统的几何结构的关联维数，g为极差。

通过 G-P 算法估计动态系统的关联维，对于每一对嵌入向量Xi和Xj计算它们之间的欧氏距离dij：

dij=∑mk=1（x（i+（k-1）τ）-x（j+（k-1）τ））2

对于给定的半径 ，计算出在该半径范围内与每个点Xi关联的点的数量Ni（），然后计算处所有点的平均关联数〈N（）〉，即在给定半径下的平均关联数。

最终，通过计算对数关联数和对数半径之间的斜率来估计关联维d：

d=lim→0ln〈N（）〉ln

α向量可以作为对云南板块指数系统的一个综合度量。对于不同的序列，可能会有不同的向量 α。在特殊时期前，云南板块指数系统的混沌度为：

α（0.3123，4.4314，0.1326）

特殊时期后，云南板块指数系统的混沌度为：

α′（1.3054，2.8506，0.1400）

除了关联维数外，最大李雅普诺夫指数和极差都呈现出增加的趋势。最大李雅普诺夫指数从 0.3123 增加到 1.3054，极差从 0.1326 增加到 0.1400。这种变化暗示了系统动态的混沌特性在特殊时期得到了增强。最大李雅普诺夫指数的增加意味着微小初始差异在时间演化中扩散更快，而极差的增加可能反映了系统状态的不稳定性增加。虽然关联维数在这个情况下保持不变，但在考虑最大李雅普诺夫指数和极差的增加时，整体上系统的混沌度有所提高。

6 结论

研究表明，特殊时期后，云南板块指数的混沌度明显增加，表明在特殊时期影响下，云南板块的市场表现出更为复杂和不确定的动态行为。混沌度的增加意味着市场中的变动更加不可预测，波动性增强，投资者难以准确预测市场走势。

在特殊时期前，云南板块指数可能表现出较为稳定的市场趋势。2019年12月后市场出现剧烈波动使市场变得更加复杂。

总之，云南板块指数在特殊时期前后混沌度的增加表明了市场中更为复杂和不可预测的动态行为。这种趋势提醒着投资者在不确定时期更加谨慎，需要采取适当的风险管理策略来应对市场的波动性增加。

参考文献：

[1] BAHAR A， ERDAL B， THABET A. Fractional economic models based on market equilibrium in the frame of different type kernels[J].Chaos， solitons & fractals，2020（130）.

[2] AMOS C， ANDREA L，CHALKER J T. Spectral Lyapunov exponents in chaotic and localized many-body quantum systems[J].Physical review research， 2021，3（2）.

[3] NDOLANE S. Analysis of a fractional-order chaotic system in the context of the Caputo fractional derivative via bifurcation and lyapunov exponents[J].Journal of King Saud University-Science，2021， 33（1）.

[4] YANG Z Y， JIAO P P， YUN X，et al. Kalman filtering short-term traffic flow prediction model based on phase space reconstruction[J].Journal of Beijing Institute of Civil Engineering & Architecture， 2021，37（4）.