基于XGBoost的多重加权谱比降噪方法

韩复兴,宋炳宣,陈雨贝,吴林骏,黄梦婷,潘延杰

吉林大学地球探测科学与技术学院,长春 130026

0 引言

微动H/V谱比方法(又称HVSR(horizontal to vertical spectral ratio)方法)是一种快速、经济的非侵入探测方法,它在城市地球物理勘探中发挥重要作用。1989年日本学者Nakamura[1]率先提出用同一地表测点地脉动水平分量与竖向分量的傅里叶幅值谱比值,即H/V谱比,来估计场地的共振频率和放大因子。H/V谱比法认为H/V谱比曲线的峰值频率对应于场地剪切波的共振频率,通过该频率可以获得场地的放大系数和沉积层厚度,进而推测地下地层构造。

微动H/V谱比方法对于划分土石分界面、检索剪切波阻抗变化等信息实际应用效果好,且具有便捷高效、勘探周期短的优点。与野外地球物理勘探相比,城市地球物理探测一方面精度要求高,另一方面需要考虑城市复杂的噪声和人文环境[2-3]。微动H/V谱比方法作为以非地震引起的微弱震动为观测对象的非侵入探测方法,契合以上两方面特点,故在城市地球物理勘探中应用较多。但城市中震动干扰因素众多,如车辆震动噪声、施工噪声等,采集的一手谱比数据用于谱比计算效果较差;因此需要对原始的三分量数据进行信噪分析,获得精细化处理后的优质谱比曲线。

H/V谱比法的数据精细化处理环节可在时域和频域上分别或结合进行。文献资料表明,目前国内外基于时域识别瞬态干扰信号多采用长短时窗平均振幅比(short time average/long time average, STA/LTA)方法[4],如:2018年Setiawan等[5]在南澳大利亚州阿德莱德市进行了环境噪声测量,在此基础上通过STA/LTA方法排除瞬态干扰,选择环境噪声中最稳定的部分,并运用H/V谱比法研究地震场地划分;张若晗等[6]选用微动H/V谱比法对济南中心城区的土石分界面展开研究,在计算每个时窗的H/V谱比之前先采用反触发STA/LTA方法剔除瞬态干扰;在SESAME(site effects assessment using ambient excitations)团队的H/V谱比技术实施指南中[7],该算法也被推荐用于时窗选择。

同样是基于时间域,2016年D’Alessandro等[8]提出通过层次聚类算法实现时窗的自动选择。该算法通过提取HVSR曲线的自洽聚类来对数据进行处理,消除了STA/LTA方法中阈值和时窗长度选取的主观因素影响,提高了数据分析的客观性。

近年,基于频域的降噪算法也逐渐得到研究者的关注。Cox等[9]提出了一种基于频域的拒绝算法,在进行计算时,该方法可有效剔除峰值频率与峰值频率均值相差过大的时间窗口,对数据进行降噪。Dal等[10]同样通过谱比曲线峰值提出了对多峰谱比曲线进行降噪的频域方法。

此外,2015年Liu等[11]结合希尔伯特-黄变换适合处理非平稳信号的特点,提出采用希尔伯特-黄变换来对微动数据进行分析。该方法通过经验模态分解,将原始信号分解为固有模态函数,并将频率最高的固有模态函数去除,剩余部分作为微动信号的有效部分进行希尔伯特-黄变换以实现对原始信号的去噪处理。

除了自动降噪算法,还有一些人工方法被用于降噪,例如:根据数据使用带通滤波器,使用0.5～20.0 Hz的带通滤波器对福州地区进行微动探测[12];或对图谱进行目视检查,手动删除受局部干扰影响的部分[13]。

上述方法在实际运用过程中均存在面对高噪声数据信号提取困难、受主观因素影响大、参数调整困难等问题。对此,本文提出一种基于XGBoost(extreme gradient boosting)的多重加权谱比方法对谱比曲线进行预处理操作,从而实现较高噪声下的微动信号提取。本方法在训练集建立后,只需将原始数据读入软件即可自动完成信号提取,在提取过程中无需调参,降低了微动数据信号提取的工作量,实现了微动信号噪声压制的智能化。

1 算法技术路线

1.1 多重加权谱比算法

微动数据可用时间序列X(H1,H2,V)表示(H1、H2为水平分量,V为垂直分量)。在数据处理过程中,X应由X′(f,I,H/V)代替(f为样本点频率,I为样本点傅里叶频谱幅值,H/V为水平分量与垂直分量的傅里叶幅值比)。显然,仅从X′的3个维度(f,I,H/V)难以直接判断该采样点是否为噪声,故应对X′进行升维,在更高维空间中寻找噪点与信号的特征。

1.1.1 幅值加权谱比

幅值加权谱比可表示为

(1)

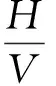
由原始谱比数据(图1a)与幅值加权的谱比数据(图1b)对比可见,具备稳定信号且谱比值较大的数据位于幅值加权谱比曲线的顶端。

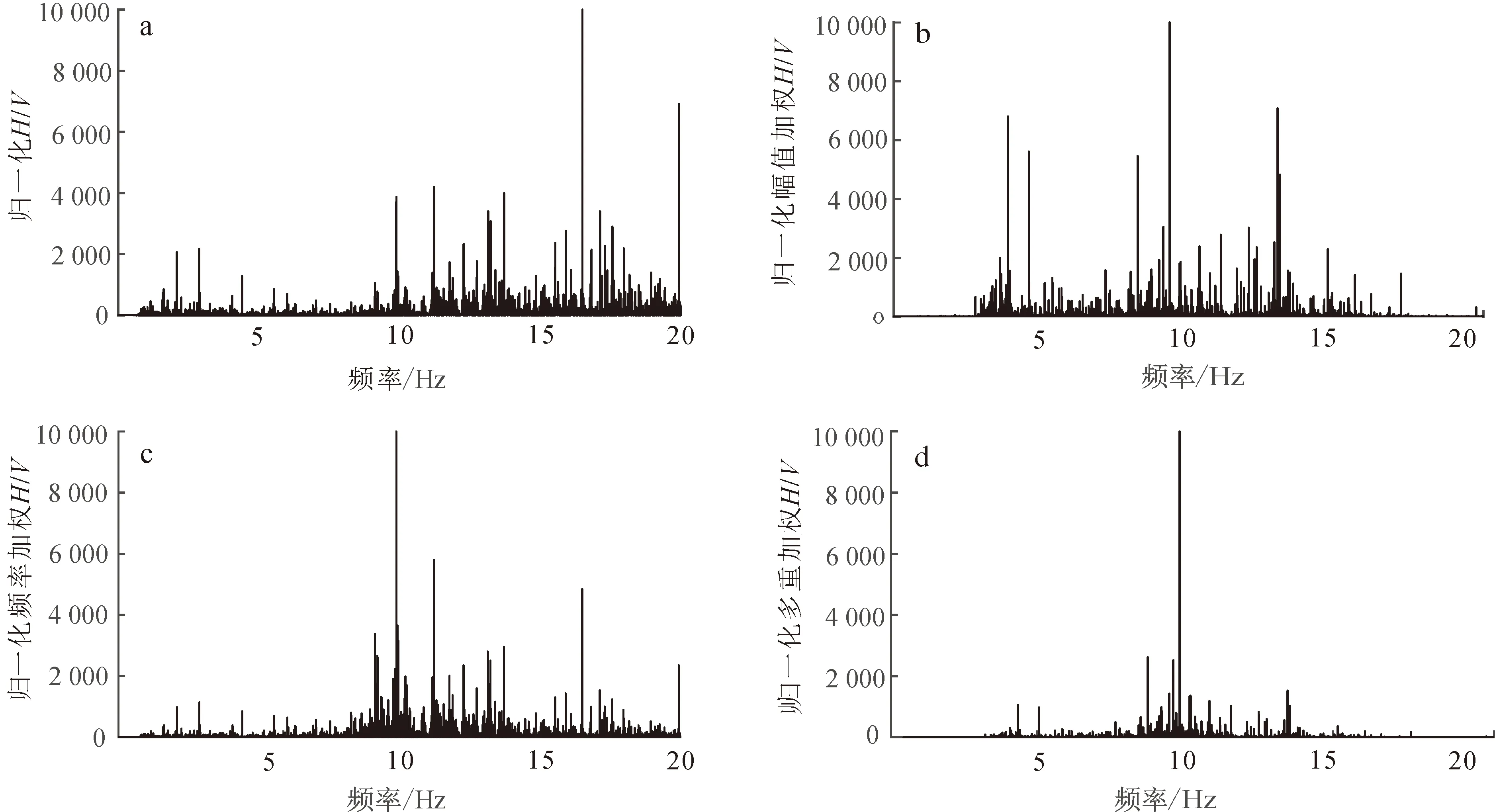
a. 原始谱比数据;b. 幅值加权谱比;c. 频率加权谱比;d. 多重加权谱比。

由地脉波稳定、长周期的特点可知,加权谱比应当筛选出幅值稳、谱比接近峰值的采样点。故引入经验常数λ,一方面改造了极点,使程序简单,另一方面符合加权谱比的意义。加权谱比是幅值赋权下的H/V,采样点的加权谱比值应由幅值与H/V值共同决定,加权后二者对加权谱比的数值影响相当。

1.1.2 频率加权谱比

常见H/V谱比曲线有个明显的峰值频率,单台数据无法区分微动是由体波还是面波组成,很难判断H/V峰值是由体波中的剪切波在松散沉积层的共振引起,还是由瑞利面波的极化作用或勒夫波的震相引起。通过Sylvette等[14]的模拟实验发现,微动H/V谱比曲线峰值频率与波场组成关系不大,而与松散沉积层的共振频率相吻合,峰值频率接近或等于松散沉积层的共振频率。从场地效应的传递函数出发,可推导出H/V谱比曲线峰值频率与松散覆盖层的平均剪切波速和厚度的关系如下:

(2)

式中:f0为H/V谱比曲线峰值频率;vS为覆盖层平均剪切波速;Dov为松散覆盖层厚度,可由测井等工程资料直接获得。H/V谱比曲线关注峰值频率,故给出频率加权谱比:

(3)

如图1c所示,在频率加权谱比曲线中,兼具信号位于峰值信号附近且谱比值较大的数据处于加权谱比曲线的顶端。

1.1.3 多重加权谱比

由式(1)(3),可定义多重加权谱比:

(4)

如图1d所示,在多重加权谱比曲线中,兼具信号稳定、位于峰值信号附近且谱比值较大的数据处于加权谱比曲线的顶端。

由式(1)(3)(4)可对X′进行升维,得到

由地脉波稳定的特点与HVSR对峰值频率的需要,可得信号点均位于X″中多重加权谱比曲线的顶端,故经升维后的X″可在此高维空间中将信号与噪声较好地分离。

1.2 XGBoost算法

(5)

XGBoost旨在通过迭代方式集成弱分类器以形成预测精度和鲁棒性更高的模型。每一次迭代都是在前一步的基础上增加一棵树,而新增的树视为拟合上次预测的残差。迭代过程为:

(6)

目标函数是研究一切机器学习问题的出发点,求解目标函数最低数值即为求解机器学习问题解。XGBoost的目标函数由损失函数和正则项两部分组成。正则项用于控制模型的复杂度,模型的预测精度由偏差和方差共同决定。由于本研究面向成分复杂、易出现极端数值的微动数据,故需要利用正则项防止模型过拟合:

(7)

式中:T为节点数量;ωj为叶子节点j的分数;γ和ε均为系数。

综上,XGBoost的目标函数为

(8)

XGBoost采用增量训练的方式进行迭代,以最大化减小目标函数值。在t轮迭代之后,目标函数更新为

(9)

为了使损失函数梯度收敛更快、更准确,XGBoost利用泰勒展开式对所有二阶可导的损失函数做近似替换,目标函数近似为

(10)

将每个数据的损失函数叠加,去掉无关项,得到

(11)

(12)

上述ωj相互独立,当新增树的结构已知时,可以求得叶节点对应的最优权重和最优目标函数:

(13)

(14)

在实际运用中,只需保存训练好的XGBoost模型,并将待预测数据输入使用即可。

1.3 训练集建立

幅值在幅值均值附近的信号符合地脉波稳定的特征,实际应用效果显示,对干扰较大的数据,幅值中位数对幅值均值的衡量效果优于幅值算术平均值的衡量效果;因此,将傅里叶频谱幅值位于幅值中位数邻域的信号标注为关注信号。频率方面,用地层已知的HVSR曲线进行训练集建立,将f0邻域内的数据标注为关注信号,对基频进行重点提取。对地层未知的曲线可选取关注的频率窗口,如本文采取频率位于0.05～20.00 Hz之间的信号为有效信号,实现关注窗口的重点提取。综合上述,幅值与频率的选取可建立训练集。

1.4 算法适用范围分析

显然,本算法流程中多重加权谱比算法的建立效果决定了本算法的适用范围。对于受低频高振幅噪声污染严重的微动数据,如图2所示,有效信号幅值远小于干扰数据幅值,加权谱比算法建立效果较差,难以提取有效信息。

a. 南北方向;b. 东西方向;c. 垂直方向。

2 实测微动数据信号提取分析

为了检验基于XGBoost的多重加权谱比降噪方法的有效性,本文应用该方法与STA/LTA方法分别对吉林大学朝阳校区的微动谱比数据进行处理。朝阳校区临近文化广场,有多种文娱活动在此开展,噪声复杂,干扰较大。图3为三分量微动仪记录的原始数据,可见前72 s内信号幅值巨大,72 s后信号幅值难以辨认。图4为较大干扰事件的局部数据放大图,可见前72 s干扰严重。

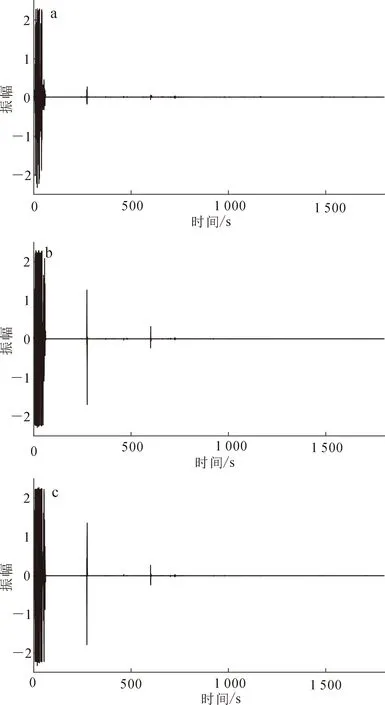
a. 南北方向;b. 东西方向;c. 垂直方向。

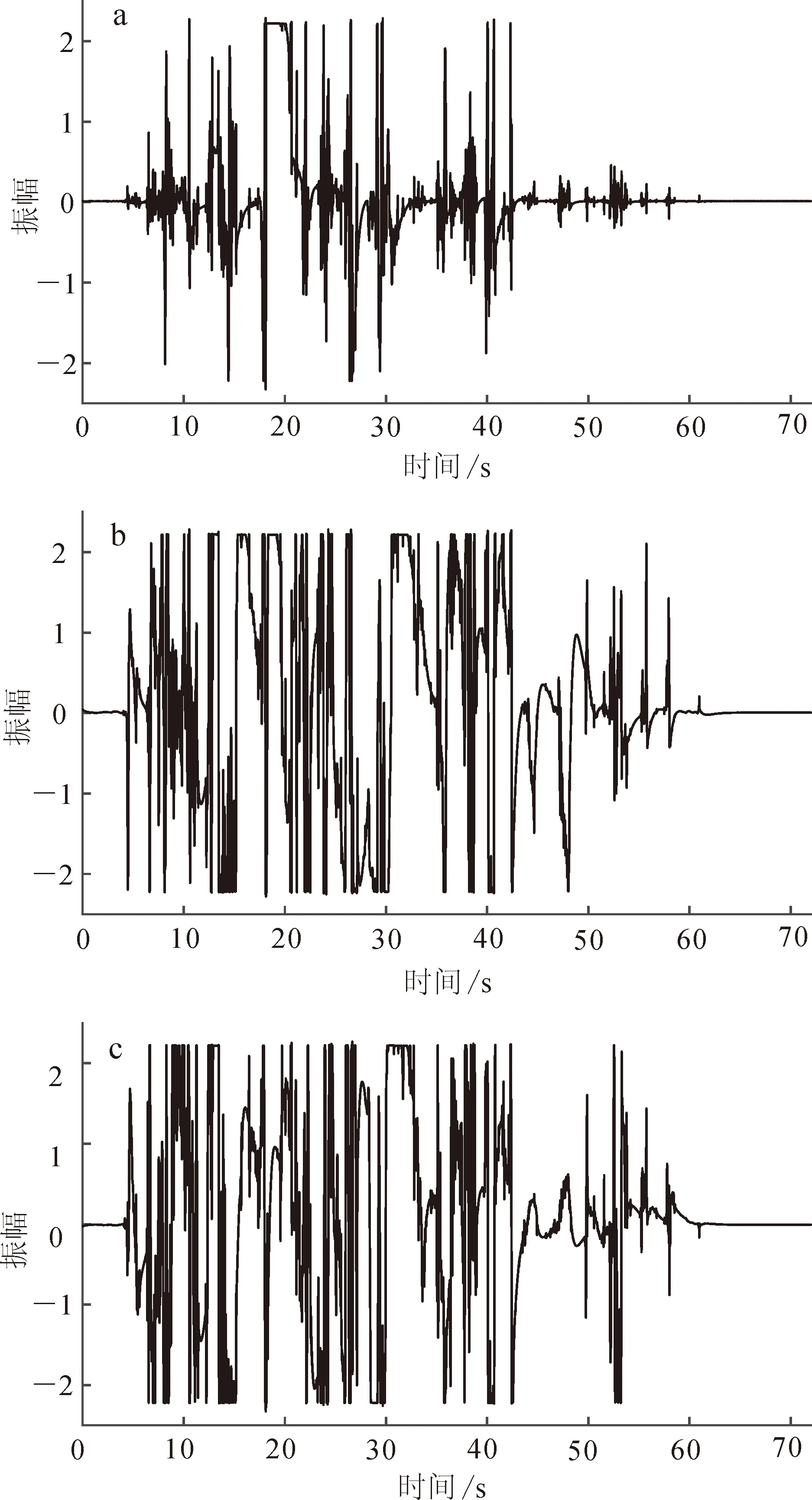
a. 南北方向;b. 东西方向;c. 垂直方向。

图5为STA/LTA方法筛选后的时间序列数据,可见前72 s存在的大振幅干扰事件并没有被去除,这是STA/LTA方法固有缺陷所导致的。在STA/LTA方法中,阈值的设定和时窗的选取具有主观性且对降噪效果的影响较大。阈值和时窗主要基于统计规律来确定,当高振幅噪声持续时间较长、超过长时窗所截时段,且阈值选择较高时,该噪声难以被去除。而时窗选择过长,阈值选择较低,可能导致有效信息不足。在该组数据的处理中,前72 s内的噪声持续时间长、振幅大,故STA/LTA方法难以去除,且过滤了较多有效信息,导致谱比曲线峰值不清晰。

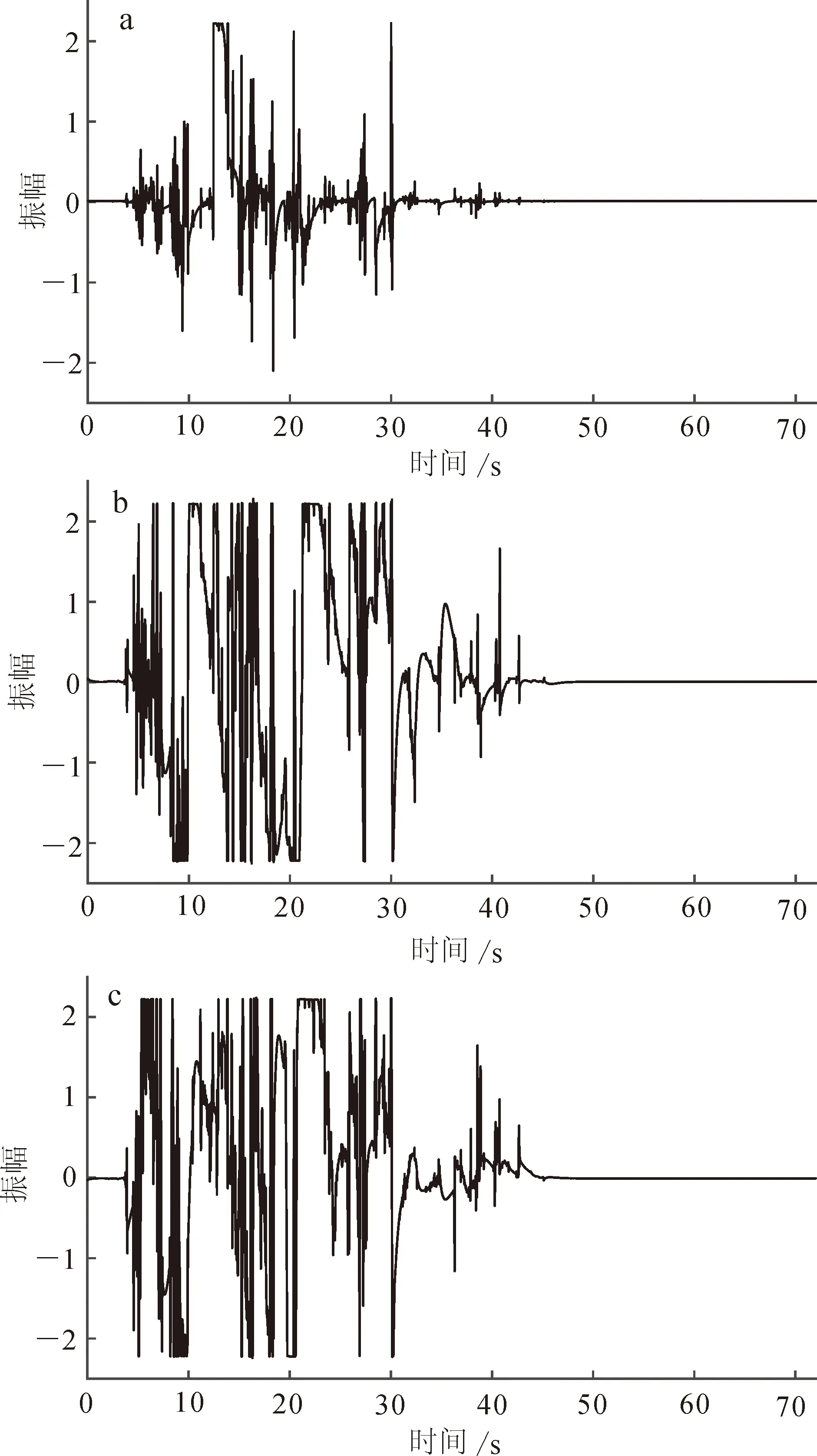
a. 南北方向;b. 东西方向;c. 垂直方向。

分别对该信号利用STA/LTA方法与本文方法进行信号提取,图6为两种方法提取结果的谱比曲线。可见本文方法基频峰值与高频的谱比峰值均得到有效提取,SLA/LTA方法难以识别曲线峰值。在面对较复杂环境时,STA/LTA方法难以识别微动信号中的有效数据,导致谱比曲线峰值无法识别,本文方法可清晰识别谱比曲线峰值。

图6 STA/LTA方法(a)与多重加权降噪方法(b)谱比曲线对比

在智能化程度方面,相较于STA/LTA方法需要依靠经验判断时窗与阈值,本文方法在模型训练结束后,无需调整任何参数即可实现信号提取,实现信号提取智能化,增加提取结果客观程度,减少因调参产生的主观性和不确定性。

在算法效率方面,使用平台为AMD RyzenTM7 5800H 3.2 GHz。由于本算法的计算时长主要取决于使用模型大小,以16 GB模型为例,本文方法用时728 s,STA/LTA方法用时28 s。虽然用时大幅上升,但STA/LTA方法无法处理上文中的高噪声微动数据,且本文方法使用时无需调参,更为智能化。

3 结论

1)本文针对复杂环境下高噪声微动数据的降噪需求,提出了基于XGBoost的多重加权谱比降噪方法。

2)对高噪声的实际数据应用显示,本文方法信号提取的准度优于STA/LTA方法。同时,本文方法在模型训练完毕后无需调整参数,在智能化程度上也优于传统STA/LTA方法。但本文方法训练模型较大,耗时较长,在干扰信号振幅大于微动数据振幅时方法失效。

针对本文方法的缺陷,未来将重点研究干扰信号振幅大于微动数据振幅的强干扰数据信号提取,并加入并行算法,使现有方法运行效率更高。