干砂小应变动力学参数的弯曲元试验

刘红帅,宋东松,张东涛,李延冰

1.河北大学岩土工程研究所,河北 保定 071002

2.河北极致地震预防服务有限公司,河北 保定 071027

0 引言

在岩土工程实践中,土体的小应变动力特性对分析土方支护结构、预测地基变形以及由于振动引起的地面地震响应等问题起到重要的作用。目前,土体的小应变动力参数通常采用弯曲元或共振柱获得。弯曲元技术的原理简明、易于操作,已被广泛安装在室内试验设备(共振柱、动三轴)中进行土体的小应变动力参数测量研究,并取得了大量研究成果[1-6]。

弯曲元主要通过测试P波(压缩波)和S波(剪切波)在土体介质中的传播时间,确定土体的剪切波波速vS和压缩波波速vP:

(1)

式中:vS或P为剪切波波速或压缩波波速,m/s;Ltt为波传播距离,m;Δt为波的传播时间,s。

然后基于波动理论计算出相应的剪切模量G0和侧限模量M0:

(2)

式中,ρ为土体密度,g/cm3。

最后根据各动参数与泊松比μ之间的关系可以相互转换:

(3)

式中:E0为杨氏模量,MPa;K0为体积模量,MPa。

然而在使用弯曲元测试时,波形、频率、峰值和试样的尺寸[7-13]对波在土体中传播时间的确定会造成一定的影响,尤其对S波传播时间的确定更为明显。现有的研究中主要从输入波的频率方面来研究其对输出信号传播时间确定的影响[10-13],结果表明输出波频率对S波有明显的影响,随频率的增大确定的传播时间越来越小。但从输入波峰值、输入波形对传播时间的影响研究较少,因此研究它们对M0、G0和μ的影响具有一定的意义。

弯曲元中传播时间的确定还存在另外一个问题,即到目前为止也没有给出统一的数据处理方法用于确定波的传播时间。目前对波的传播时间的确定主要分为时域法和频域法两类。其中,时域法包括初达波法和峰值法,频域法包括互相关法和交互功率法。多数研究者对上述方法确定的结果有不同的见解:Viggiani等[1]认为,频域互相关法和交互功率法能给出较准确的结果,而时域初达波法由于受到近场效应的影响会高估剪切模量14%以上;Greening等[10]认为,时域初达波法跟频域法相比严重高估了剪切模量,程度可达1倍以上;但Leong等[11,13-15]则认为,时域初达波法能比较可靠地确定S波传播时间;Yamashita等[16]综合分析了弯曲元国际平行试验的信号,认为时域初达波法的结果离散性总体上比时域波值法和频域法小,且更加接近参考值;Youn等[8,17-18]将弯曲元与共振柱试验进行对比,更有助于弯曲元剪切波传播时间的准确确定。

根据以上的研究可以看出,研究者大多仅从输入波的频率方面来研究其对输出信号传播时间确定的影响,而对输入波峰值、输入波形对输出信号的影响研究较少。基于此,本文利用弯曲元对干燥福建标准砂进行P波和S波测试,分析P波和S波在干燥福建标准砂中的传播特性,研究输入频率、输入波峰值、输入波形对输出信号的影响,并对不同信号分析方法确定的结果进行对比。最后在对土体相对密度和围压对M0、G0和μ的影响研究基础上,根据现有的Hardin模型[19],给出考虑围压和孔隙比耦合作用下的M0、G0和μ的三维模型公式,以期为实际工程中对M0、G0和μ的估算提供一定的参考。

1 试验设备及方案

1.1 试验设备

本次试验采用的是西安康拓力公司生产的弯曲元测试系统,如图1所示。弯曲元安装在动三轴仪器上,弯曲元的宽为11 mm,厚为1.2 mm,插入土的深度为3 mm,通过在控制软件中的选择,能方便地进行P波和S波的测试。经标定弯曲-伸展元(将发射端和接收端直接接触),该测试设备的系统延时为0.036 ms。

图1 弯曲元动三轴测试系统示意图

1.2 试验方案

试验采用粒径为0.10～0.25 mm的福建标准砂作为研究材料,福建标准砂的颗粒级配如图2所示。福建标准砂的物理性质在实验室中测定,如表1所示。

表1 试样基本物性性质

图2 福建标准砂颗粒级配

试样采用直径d=50 mm、高H=100 mm的干砂样。采用干砂装样法装样,共分5层均匀制样,严格控制每层厚度为20 mm,装完砂样后用游标卡尺测出试样的初试高度和直径,测量试样上、中、下3个位置的直径(d1、d2、d3),最后取1/4(d1+2d2+d3)作为试样初始直径。试验采用3种不同的相对密度(Dr=30%、50%、70%)和6种不同的有效围压(σ3=50、100、300、500、700和900 kPa)进行试验,具体试验方案见表2。

表2 试验方案

2 S波、P波传播时间的影响因素分析

2.1 频率影响

图3给出了有效围压为50 kPa、相对密度为70%时,不同输入频率下S波和P波的输出信号特征。从图3可以看出,采用初达波法确定剪切波的传播时间受频率的影响较为明显,随频率的增大剪切波的传播时间在逐渐减小;但压缩波的传播时间基本上不随频率的改变而改变,这一结论与董全杨等[2,6,8,13]研究的结论相符。

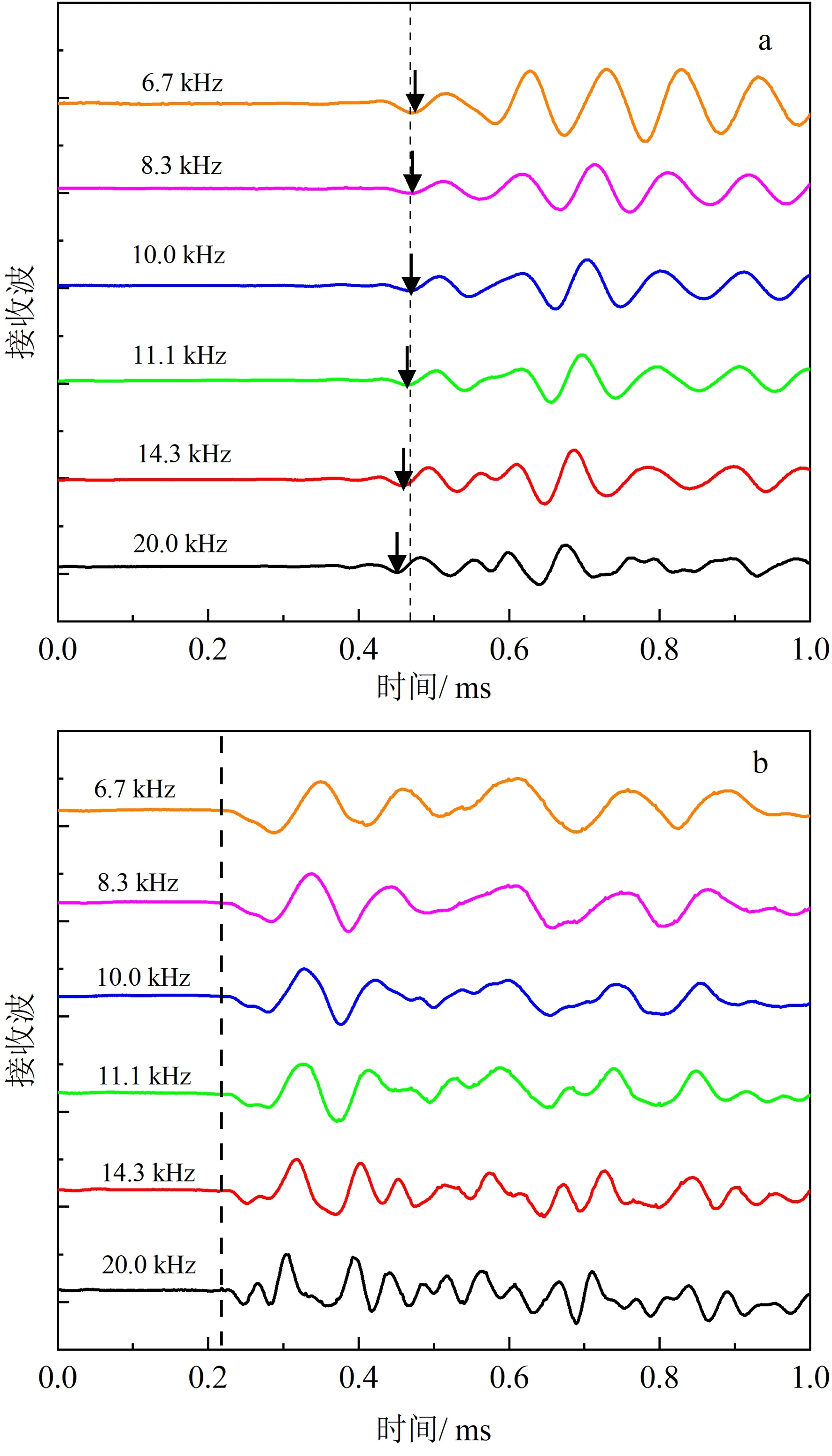
a. 不同激发频率下干砂试样中S波信号;b. 不同激发频率下干砂试样中P波信号。

2.2 传播时间确定方法的影响

本文对初达波法、峰值法和互相关法3种不同方法确定的S波的传播时间进行分析,3种方法确定S波传播时间的示意图如图4所示。图4中S1、S2为初达波法可能的到达点;P0为峰值法的起跳点,P1、P2为峰值法可能的到达点;C1、C2为互相关法可能的到达点。互相关法是由Viggiani等[1]提出的,其是通过分析激发信号与接收信号之间的相关程度来确定信号的传播时间。

图4 不同方法确定S波传播时间的特征点

图5给出了采用3种方法确定的剪切模量结果,由于本文没有在共振柱测试系统中进行弯曲元试验,为能较准确地判别3种方法采用哪个到达点确定的结果更为可靠,参考已有文献[20](σ3=50 kPa、Dr=70%、粒径为0.5～1.0 mm的福建标准砂)中与本文工况基本一致的共振柱结果。从图5可以看出:3种方法采用第一个到达点确定的结果(图5实线)与共振柱结果较为接近,而采用第二个到达点确定的结果(图5虚线)严重偏小。故下面仅针对3种方法采用第一个到达点确定的结果进行分析。初达波法和峰值法确定的G0受频率的影响较为明显,随频率的增大G0也在逐渐增大,且初达波法确定的G0均高于峰值法确定的G0;而互相关法确定的G0仅在频率小于8.3 kHz时稍大,在8.3～20.0 kHz之间时G0基本一致,且小于共振柱结果。当频率在8.3～11.1 kHz之间时,3种方法确定的G0差异性较小,且初达波法确定的G0最接近共振柱结果。以上结果表明,初达波法确定的结果相对合理,另外2种方法确定的结果基本均小于共振柱结果。为保证结果的一致性,下面的分析取S0-S1对应结果作为试样的结果。

图5 不同确定方法确定的剪切模量

2.3 输入波峰值的影响

图6给出了不同输入波峰值下输出信号图。从图6中可以看出,不论是对剪切波还是压缩波传播时间的确定,输入波峰值的大小均对判别的结果没有影响。但当输入波峰值过大时,会在峰值处出现一段小的平台段(如图6中输入波峰值为12 V时),当采用峰值法确定波传播时间时,会对峰值起跳点P0的确定产生明显影响。因此,在进行弯曲元试验时尽量控制输入波的峰值不要过大。

a. 剪切波;b. 压缩波。

2.4 输入波形的影响

图7给出了3种不同输入波形下S波和P波典型输出信号的结果。从图7可以看出:尽管3种输入波的波形差别明显,且3种输入波的传播时间有明显的差别,但输出波的波形基本类似,没有明显的差别。如图8所示,给出了3种不同输入波下确定的G0、M0和μ。从图8可以看出:输入波为雷克子波确定的G0和M0最小,输入波为三角波确定的G0和M0位于中间,输入波为正弦波确定的G0和M0最大。随着有效围压的增大,3种波形确定的G0和M0的差值也在逐渐增大。输入波为正弦波和三角波确定的μ差异性较小,其中正弦波确定的μ稍大于三角波,雷克子波确定的μ小于另外2种波形;随有效围压的增大3种波形确定的μ的差值变化不明显。

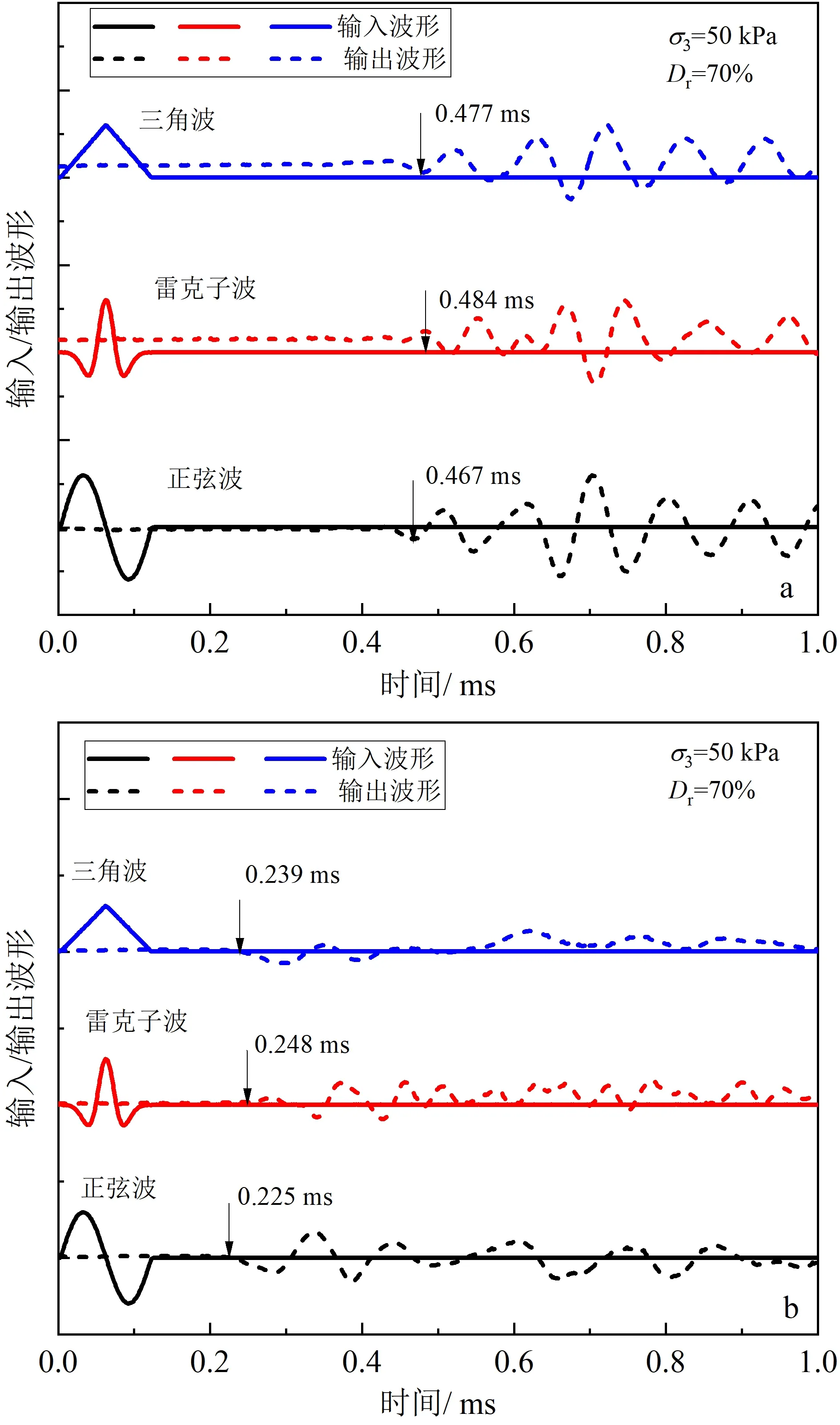
a. 剪切波;b. 压缩波。

a. 剪切模量;b. 侧线模量;c. 泊松比。

3 结果分析

3.1 剪切模量和侧线模量

为定量分析围压、孔隙比与剪切模量和侧线模量的关系,采用Hardin模型[19]对其进行分析

(4)

式中:A、B为拟合参数;F(e)为孔隙比函数,e为土样固结完成后的孔隙比,本文采用F(e)=ex的形式进行拟合。

现有大多研究均采用式(4)单独对围压或孔隙比进行拟合,用于分析围压或孔隙比对G0和M0的影响,而关于孔隙比、围压耦合作用下对G0和M0的影响研究则相对较少。故对本文采用式(4)对试验数据进行拟合,得到了G0和M0随孔隙比和围压耦合作用下的曲面图,如图9所示。从图9可以看出:G0和M0试验数据与拟合曲面有非常高的吻合性,能够较好地显示出围压和孔隙比对G0和M0的影响,G0和M0均随围压的增大呈指数形式增大;而随孔隙比的增大呈指数形式衰减,符合已有的结论[12-13]。从图9还可以看出:G0围压拟合参数0.574大于M0围压拟合参数0.390,表明G0比M0受围压的影响更敏感,随着围压的增加,G0比M0增加得更快;G0孔隙比拟合参数-2.520的绝对值大于M0孔隙比拟合参数-1.720的绝对值,也表明G0比M0受孔隙比的影响更敏感,随着孔隙比的增加,G0比M0衰减得更快。从G0和M0的三维结果图中也可以清晰地看到:G0的拟合曲面呈金字塔型分层,受围压和孔隙比的影响更大,而M0的拟合曲面的分层较为均匀,受围压和孔隙比的影响比G0的小。

a. 剪切模量与围压和孔隙比的关系;b. 侧线模量与围压和孔隙比的关系。

3.2 泊松比

在动三轴试验中,把土体的动弹性模量和动轴向应变换算动剪切模量和动剪应变的过程中,动泊松比是一个重要参数,因此其取值的合理性对换算的动剪切模量和动剪应变结果有重要的影响。现有研究[4-5,13]表明,泊松比与侧线模量和剪切模量有相同的性质,也随孔隙比的增大呈指数形式增大,随围压和剪切模量的增大呈指数形式衰减。故文中也采用式(4)对泊松比试验数据进行拟合,用于分析孔隙比和围压耦合作用下μ的变化规律,如图10所示。从图10可以看出:拟合曲面与试验值之间吻合较好,说明采用公式(4)预测μ在孔隙比和围压耦合作用下变化是合理的;μ的围压拟合参数是-0.180,小于0,表明μ随围压的增大呈现指数形式的衰减;μ的孔隙比拟合参数是0.690,大于0,表明μ随着孔隙比的增大呈指数形式增大,与前人[4-5,13]结果一致。

图10 泊松比与围压和孔隙比的关系

图11给出了泊松比随剪切模量的变化曲线图。从图11可以看出:μ随G0也呈指数形式的衰减;与μ的围压拟合参数-0.180相比,μ的剪切模量拟合参数-0.349更小,表明μ受G0的影响比围压更明显。

图11 泊松比与剪切模量的关系

3.3 与现有成果对比

本文与前人的弯曲元试验结果进行了对比。表3给出了孙奇等[12]和Gu等[13]试验所用福建标准砂的基本物理指标。为消除孔隙比对结果的影响,对本文的试验结果和现有的成果[12-13]进行孔隙比均一化处理(除以孔隙比F(e)=ex),图12给出了本文试验与现有成果的剪切模量和侧线模量。从图12可以看出:不同类型的砂土的G0和M0随围压的变化均表现出一致的规律性,即随围压的增大而呈现出指数形式的增大,且G0随围压增大的增长速度比M0快;不仅3种不同类型的砂土,即使是同一类型的砂土测得的M0和G0结果也有明显的差异性;这可能是由于粒径大小、颗粒级配、砂土类型等因素的影响。值得说明的是,与孙奇等[12-13]对福建标准砂测得的G0和M0结果相比,本文的试验结果位于中间部分,孙奇等[12]的试验结果较大,大体上分为上外包络线,而Gu等[13]的试验结果较小,大体上分为下外包络线。结合图2和表3中福建标准砂的基本物性指标结果可以看出,造成这种现象原因可能是由于试验选用砂土的颗粒级配不同造成的。

表3 文献中福建标准砂土试样基本物性性质

a. 剪切模量;b. 侧线模量。

4 结论

1)S波受输入频率的影响较为明显,P波基本不受频率的影响。

2)不论是对剪切波还是压缩波时延的确定,输入波峰值的大小均对判别的结果没有影响。但当输出波峰值过大时,会在峰值处出现一段小的平台段。

3)当输入波形不同时,会对测试的侧线模量、剪切模量以及泊松比产生显著的影响。

4)侧线模量、剪切模量、泊松比均随有效围压和孔隙比的增大呈指数形式变化,并根据Hardin提出的小应变模量预测模型,拟合出了考虑围压和孔隙比耦合作用下的三维模型公式,可为实际工程中对M0、G0和μ的估算提供一定参考。