热变形对饱和黏性土渗透系数的影响

王福刚, 杨国华, 程 辉, 管小桐, 袁益龙

1.地下水资源和环境教育部重点实验室(吉林大学),长春 130021

2.吉林省水资源与水环境重点实验室,长春 130021

0 引言

渗透系数是水文地质、油气开采、地热资源等多领域渗流研究的重要参数。水文地质渗透系数与土壤颗粒的粒径分布有关,并受到流体性质、土壤矿物、温度、固结压力等条件的影响[1-3]。已有研究[4-5]表明,渗透系数变化与温度变化呈正相关,温度是影响渗透系数的重要因素。

温度变化可以引起流体密度和黏度变化,进而改变渗透系数。在不考虑温度效应对介质渗透率或土体微观结构影响的条件下,可以通过流体黏度与温度的关系预测温度对渗透系数的影响[4,6-10]。然而,温度的变化不仅会影响孔隙中流体的性质,还会影响土体的微观结构,进而影响土体的渗透性[11-14]。只考虑温度与流体性质的关系对渗透系数的影响,从理论上来说是不够严谨的,会造成实验中实测值与计算值不一致[5,15-18]。

目前,关于温度对土体结构影响的研究主要关注于黏性土的热变形效应,因为与粗颗粒土相比,细颗粒土更易受到温度变化的影响[15,19-21]。温度循环变化会引起土体的体积变化,并随着循环次数增加,出现不可逆的体积变形[13,22]。

一些研究[11,23]表明,冻融过程中温度变化会引起土体结构变化,导致孔隙率和渗透率发生变化。部分学者对20～80 ℃的温度变化引起土体结构变化进而改变土渗透性进行了相关研究[9-10]。如:Chen等[24]通过核磁共振测试研究了温度变化引起土体微观结构变化对黏土渗透性的影响,发现在无约束边界条件下加热会产生较大尺寸的孔隙并削弱微观结构,80 ℃时渗透系数是23 ℃时渗透系数的4.23倍,并提出了考虑土体应变的渗透系数演化模型;Joshaghani等[11]通过不同应力约束条件下温控实验探索了20～80 ℃温度变化对高岭土和渥太华砂渗透性及孔隙率的影响,发现渗透系数随温度升高而增加,孔隙比随着温度升高而降低。

在长期研究中,学者们考虑流体性质和介质特征构建了不同形式的渗透系数计算模型[25-33]。其中比较经典的模型包括Darcy模型[30]和应用广泛的Kozeny-Carman(K-C)模型[31]等。此外,许多学者基于K-C模型提出了各类改进模型,其中Ren等[25]提出的K-C修正模型(REN model)计算精度相对较高。

综上,温度变化引起土体形变诱导土体渗透性演化方面的研究存在以下不足:1)尽管部分学者研究了20～80 ℃温度变化对土体结构以及渗透性的影响,并提出考虑孔隙率变化的渗透系数计算模型,但模型用于黏性土低速渗流情况的渗透系数计算时,普遍存在误差偏大的问题。且模型对变温过程中水土膨胀/收缩、吸附水转换等机制表征不足。2)寒冷地区浅层地下水温度通常低于20 ℃[34-35],现有研究大多在20 ℃以上的温度条件下进行,在0～20 ℃温度范围的黏性土渗透系数实验研究与模型研究方面存在明显不足。

鉴于以上问题,本次研究通过控温实验探究5～30 ℃温度变化对黏性土渗透性影响机理,并同时考虑温度变化诱导的流体性质和土体变形对渗透系数的影响,进一步修正K-C模型,以提高模型的应用范围和精度。

1 实验材料和方法

实验采用的黏性土为中国长白山地区的白浆土[34,36],其位于吉林省东南部长白山地区的靖宇县和抚松县,地理坐标为126°30′E—127°49′E,41°42′N—42°49′N,土的风干密度约为1.45 g/cm3。土的基本参数见表1。

表1 土的基本参数

实验采用变温低渗孔隙介质渗透实验装置,装置的可控制温度范围为-20～60 ℃。土体变形利用夹持器(图1a)顶部的位移表(量程为0～10 mm,分度值为0.01 mm)进行监测。当温度变化时,夹持器内部土体产生膨胀/收缩,但由于侧面受限仅产生轴向变形,因此本次实验通过监测夹持器顶部位移表的变化量进而确定土体的轴向变形量,然后计算变形量与初始土样高度之比,进而得到应变。

图1 土样夹持器(a)与实验土样(b)

实验土样(图1b)制备是将野外采集的土壤过筛后烘干,使用专用土样压模机压实制成。试样高度为20 mm,直径为61.8 mm。试样制备完毕后,放入渗透实验夹持器,抽真空后使用纯水进行饱和。饱和完成后,进行定水头渗流实验。本次实验根据前期大量预实验,水力梯度设置为5。该水力梯度既能保证渗流过程不破坏试样内部结构,又能保证渗流时间不会过长。

本次实验的温度条件依据北方寒区可能的温度区间设定为30→5→30 ℃,具体为30、25、20、15、10、5、10、15、20、25、30 ℃。根据前期大量预实验,该温度步长既能保证监测时间不会过长,又能表征实验结果的规律性。

实验测定的渗透系数计算公式为

(1)

式中:T为温度(℃);KT为试样的等效渗透系数(cm/s),是一个依赖于温度的参数;Q为不同温度下的流量(cm3/s);L为渗透路径,即样品高度(cm);A为试样的截面面积(cm2);Δh为试样两端的水头差(cm)。由渗透系数求取渗透率的计算公式为

(2)

式中:kT为对应温度下的等效渗透率(m2);ρT为对应温度下流体的密度(kg/m3);g为重力加速度(m/s2);μT为对应温度下水的动力黏度(Pa·s)。

2 实验结果

实验测定的渗透系数、渗透率和介质的轴向应变如图2所示。由图2可见:温度从30 ℃降至5 ℃时,渗透系数逐渐降低,最大下降76.7%;温度从5 ℃升至30 ℃时,渗透系数逐渐增大,30 ℃的渗透系数是5 ℃的3.25倍。可见温度对渗透系数影响是显著的。

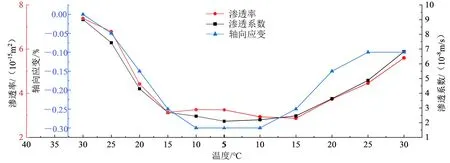
图2 渗透系数、渗透率和轴向应变随温度变化

渗透率是表征介质本身固有属性的一个参数。如果渗透率不随温度发生变化,表明介质结构不受温度影响。由于渗透系数是由流体和介质性质共同决定的参数,为了探究温度变化过程中介质结构变化对渗透系数的影响,本文计算了不同温度下的渗透率(图2)。由图2可见,无论是升温还是降温过程,温度对渗透率的影响是一个非线性过程,不同区间影响程度不一。当温度在5～15 ℃区间内,渗透率基本保持不变;温度在15～30 ℃区间,渗透率呈现明显的温度效应,这说明了在此温度区间,温度对介质的结构影响不可忽略。这与张瑜婷[17]研究0～40 ℃温度变化对黄土渗透率影响的结果相似。

由图2和3可见,温度变化过程中,黏性土发生轴向变形,位移表发生偏转。降温阶段,当温度从30 ℃下降,土样逐渐收缩,位移表下部探针下移,下降至10 ℃时,位移表的变化量达到最大值0.06 mm,轴向应变为-0.30%(图2);升温阶段,当温度从5 ℃上升,土样逐渐膨胀,位移表下部探针上移,上升至25 ℃时,位移表的变化量达到最大值0.04 mm,轴向应变从-0.3%变化到-0.1%,上升了0.2%(图2)。从降温到升温过程,通过观察位移表发现,指针最终不能回到初始值(图3),存在约0.02 mm的位移量,此时认为土体发生塑性变形,导致形变不能完全恢复。由以上实验结果分析可见,变温过程中渗透系数的计算需要同时考虑流体和介质变形的影响。

图3 实验前(a、b)后(c、d)位移表和土样变化

3 渗透系数修正模型构建

3.1 现有渗透系数模型

由经典的渗透系数计算模型(K-C模型)可见,渗透系数是介质特征、孔隙流体密度和黏度的函数。

(3)

式中:K为渗透系数(m/s);CF为多孔介质空间形状常数,无量纲;Ss为质量比表面积(m2/kg);ρm为土颗粒密度(kg/m3);e为孔隙比,无量纲。

Ren等[25]通过理论分析引入一个与孔隙比相关的参数m对K-C模型进行修正,相比其他修正方程精度较高,参数意义明确且易获取。

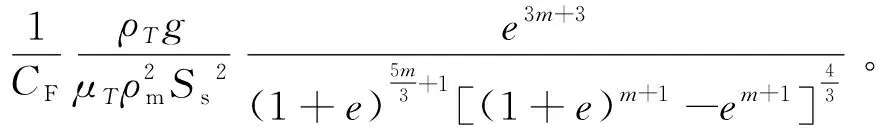
(4)

式中,m为与介质类型相关的参数,无量纲,取值范围为0～2[25]。

当只考虑温度对流体性质的影响时,不同温度下的渗透系数可以通过已知温度条件下的渗透系数进行计算,计算公式为

(5)

式中:KT0为温度为T0时的渗透系数(m/s);μT0为温度为T0时水的动力黏度(Pa·s);ρT0为温度为T0时水的密度(kg/m3);Kt为温度为T时的计算渗透系数(m/s)。

3.2 渗透系数模型的改进

现有模型在计算变温条件下黏性土的渗透系数时,大部分认为孔隙率不变,然而本研究的实验结果表明,温度变化不仅会影响水的黏度和密度,还会使土体发生变形,继而影响土的渗透性。因此,计算变温下黏性土的渗透系数需要考虑介质变形受温度的影响,进而对现有模型进行改进。改进思路为:分析土体形变、孔隙体积和水土膨胀(收缩)之间的理论关系,构建温变诱导的应变、温度和孔隙比的理论关系式,将随温度变化的孔隙比引入K-C模型的修正模型(REN模型)。

Mitchell[1]总结的水土热膨胀、排水(吸水)和体积变化之间的关系式为

(ΔVdr)ΔT=αwVwΔT+αsVsΔT-(ΔVm)ΔT。

(6)

式中:(ΔVdr)ΔT为试样排水体积变化量(cm3);(ΔVm)ΔT为试样的体积变化量(cm3);αw和αs分别是水和土壤颗粒的热膨胀系数(℃-1);Vw和Vs分别是初始温度下孔隙水体积(cm3)和土壤颗粒体积(cm3);ΔT为温度变化量(℃)。由于本次实验的试样可以发生轴向膨胀和收缩,因此可以认为本次实验为不排水条件,此时方程(6)可变换为方程(7)。

(ΔVm)ΔT=αwVwΔT+αsVsΔT。

(7)

对于饱和黏性土,孔隙体积由自由水和结合水完全充满,孔隙体积变化由自由水和结合水共同膨胀(收缩)构成,假设结合水热膨胀系数为αb(℃-1),则有

(ΔVm)ΔT=αwVf,TΔT+αbVb,TΔT+αsVsΔT。

(8)

式中:Vb,T为受温度影响的结合水体积(cm3);Vf,T为受温度影响的自由水体积(cm3)。

本研究先计算结合水受温度影响向自由水的转化量,再根据变化后的自由水体积计算膨胀(收缩)。当温度变化为ΔT(℃)时,结合水相对自由水的变化率为β(无量纲)由下式计算:

(9)

式中:ΔVb为结合水变化量(cm3);Vf为初始自由水体积(cm3)。

根据应变的定义式,可得到体积热变形与应变的关系:

(10)

式中:V为初始土的总体积(cm3);ε为应变,无量纲。自由水转化为结合水后,其性质发生变化,小水力梯度下不流动[36-37]。本研究中将结合水近似看作固体的一部分,方程(10)带入方程(8)简化得到:

ε=αwΔTn0(1-β)+αsΔT(1-n0)。

(11)

式中:n0为初始孔隙度,无量纲。依据方程(11)和实测应变进行拟合可以估计参数β。

温度变化时,孔隙度和孔隙比表达式如下:

(12)

(13)

式中:nT为温度T时的孔隙度;eT为温度T时的孔隙比;Vs,T为温度T时的固体颗粒体积(cm3);Vv,T为温度T时的孔隙体积(cm3)。联合方程(11)(12)和(13)并进行简化,得到孔隙比与温度和应变的关系式:

(14)

由于黏土矿物为多层堆叠结构,易形成大量微孔,从而导致内比表面积大于外比表面积,但可流动水,往往是沿着外比表面积通过大孔流动[26];因此模型在计算时,质量比表面积可替换为外比表面积[26],其表达式如(15)所示。

Sex=Ss/N。

(15)

式中:Sex为外比表面积(m2/kg);N为每个颗粒的平均堆叠单位层数,可以从几层到数百层不等,如,钠蒙脱石的N值为10～350,膨润土的N值为10～100[39]。

将方程(14)带入方程(4),并联合方程(15),得到改进的渗透系数计算模型:

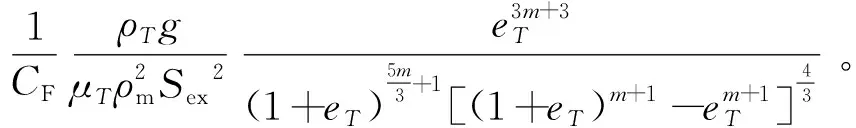
(16)

3.3 改进模型应用效果

根据实验结果,对改进的模型(式(16))以及当前可用于变温条件的渗透系数计算模型(表2)进行应用效果对比分析,进而验证改进模型的精度。

表2 渗透系数计算模型

表2中各模型的参数有明确物理意义。表3为表2所列模型的参数表,表3的参数获取方法如下:CF为介质结构相关的参数,通常视为一个经验常数,一般取值为0.2[31];m的取值与土壤性质有关,一般为0～2[25],本研究根据土壤类型,m值为0;水和土的热膨胀系数是参考现有文献给出的平均值[20,24];n0根据饱和实验得到;β可以根据方程(11)与应变率拟合得到。

表3 模型参数表

本文对比了不同模型渗透系数计算值与实测值之间的差异,一方面验证改进模型的适用性和有效性,另一方面分析介质的形变对渗透系数影响的程度。结果见图4。

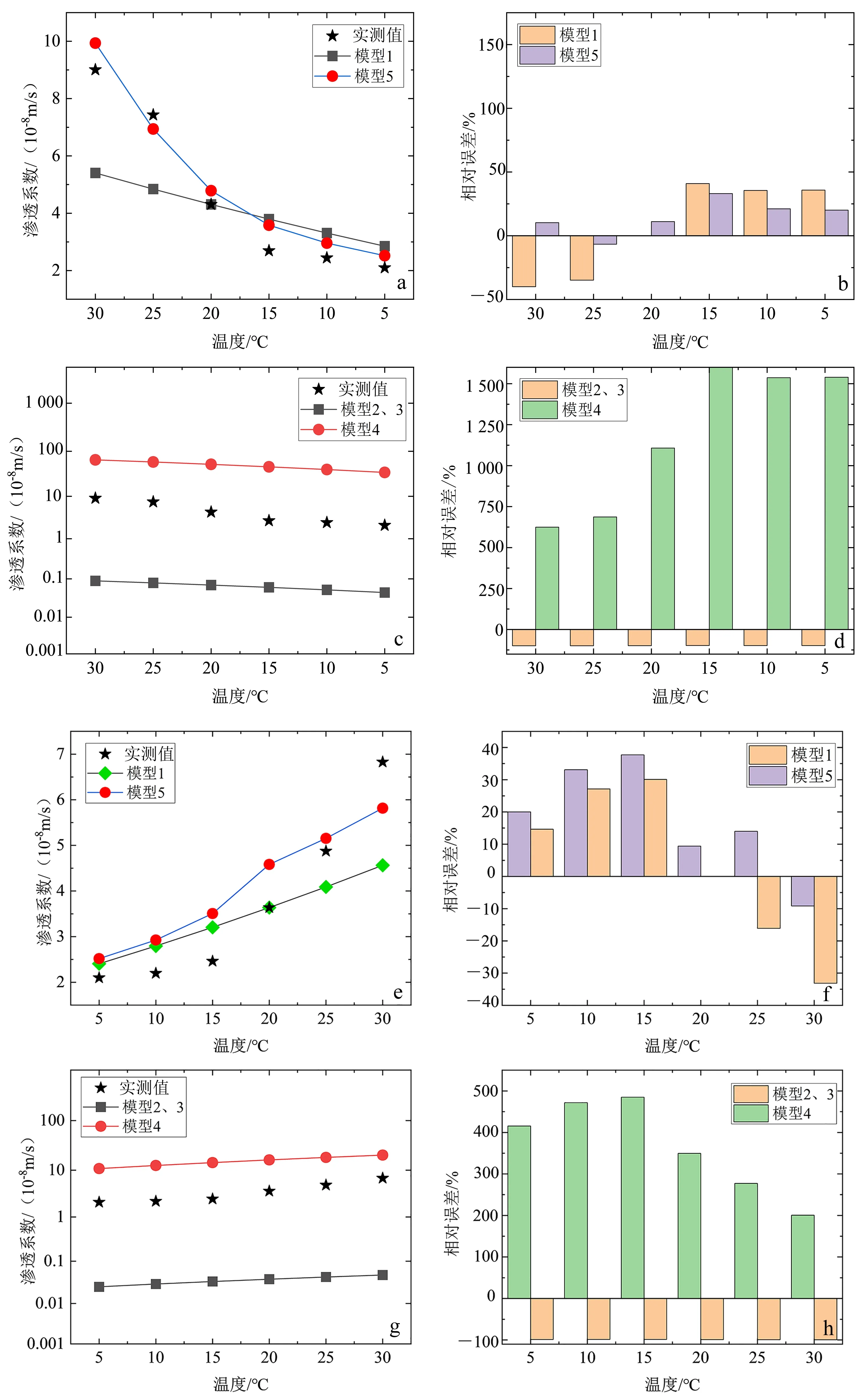
图4 降温阶段(a—d)和升温阶段(e—h)不同模型计算值与实测值对比

由于模型1、5和模型2、3、4的渗透系数计算值相差1～2个数量级,因此其计算结果分开显示。模型1和模型5在5～20 ℃范围,不论升温还是降温阶段,二者计算结果的平均相对误差接近(图4a、e);在大于20 ℃时,由于温变效应影响,二者相对误差随着温度增大逐渐增大,模型1不考虑介质结构的温变效应,最大相对误差可达40%,而考虑温变效应的模型5,平均相对误差小于20%(图4b、f)。由图4c、4g可见:模型2与模型3不论升温阶段还是降温阶段,渗透系数均远低于实测值,相差约2个数量级;模型4的渗透系数大于实测值,相差1～2个数量级。

以上进一步证明考虑介质的温度效应(孔隙比随温度变化)对渗透系数的影响是必要的。

由图4可见,不同模型中渗透系数与温度呈正相关。由流体密度和黏度的温度效应可知,温度升高,流体密度和黏度减小,流体的流动性增强,因此渗透系数与温度之间呈正相关关系。

根据图4a和4e中的模型1和模型5的不同温度区间渗透系数的对比可见:温度在5～20 ℃区间时,二者渗透系数计算值接近,这是由于模型1仅考虑流体性质,模型5同时考虑流体和介质性质;由此可推论出,5～20 ℃温度范围内渗透系数温度效应的主控因素是流体性质的变化(黏度),此温度区间介质形变对渗透系数影响较小,其对渗透系数变化的贡献率低于10%。在20～30 ℃区间,模型1计算相对误差随温度逐渐增大,而模型5计算相对误差较小;由此可推断,20～30 ℃温度范围介质形变引起渗透系数的变化不可忽略,温度引起介质形变诱导的渗透系数变化贡献率增大,经计算在此温度范围其对渗透系数变化的贡献率最大超过40%。因此,对于低渗黏性土,当温度大于20 ℃时,温度引起的介质形变效应对渗透系数的影响应该给予足够的重视。

4 结论与建议

1)温度对饱和黏性土的渗透系数影响显著,二者呈正相关。通过本文改进的渗透系数模型(模型5)分析可见,温度在5～20 ℃区间时,渗透系数变化的主控因素是流体黏度,此温度区间介质形变对渗透系数影响较小,其对渗透系数变化的贡献率低于10%;温度在20～30 ℃区间,温度变化引起介质形变诱导的渗透系数变化贡献率增大,对渗透系数影响的贡献率最大超过40%。

2)本文所列举的K-C模型(模型2)及其修正模型(模型3、4),其计算值与实测值之间相差1～2个数量级;仅考虑流体性质随温度变化的Darcy模型(模型1),计算误差最大可达40%;而本次改进的渗透系数计算模型(模型5),计算平均误差小于20%。

3)本研究的主要认识是基于小水力梯度黏质粉砂介质的变温渗流实验得到,对于纯黏土以及大水力梯度下渗透系数计算的可靠性尚需进一步研究。