栓接装配式钢-混凝土组合梁及其抗剪键的力学性能研究

陈庆伟, 王文洋*, 王志鹏, 潘晨, 肖宜凯

(1.国网山东省电力公司经济技术研究院, 济南 250021; 2.太原理工大学土木工程学院, 太原 030024)

钢-混凝土组合梁由剪力连接件紧密连接上部混凝土翼板与下部钢梁构成,其综合了混凝土结构和钢结构的优点,在桥梁工程及高层、大跨度的建筑中得到了广泛应用[1-2]。栓钉连接件因性能良好,施工技术成熟且成本较低,是应用广泛的剪力连接件[3]。随着装配式建筑的大力推广,传统钢-混凝土组合梁难以装配、拆卸的问题逐渐显露。使用高强螺栓代替传统栓钉,不仅可以实现混凝土板的预制装配、避免钢材焊接缺陷、扩大钢种选择范围,还可以使得剪力连接件的更换成为可能[4]。

目前,已有一些学者对组合梁中高强螺栓的力学性能开展了研究。Kwon等[5-6]对组合梁中内置双螺母螺栓、高强摩擦型螺栓、黏合剂锚固螺栓3种不同的螺栓进行了静力和疲劳性能研究,发现3种类型螺栓的抗剪承载力大致为其抗拉强度的一半,且螺栓连接件的抗疲劳强度明显高于栓钉连接件。杜浩等[7]通过24个推出试验发现螺栓周围混凝土受压破坏和螺栓栓杆剪断破坏两种典型破坏模式,并给出不同破坏模式下钢-混凝土组合梁螺栓连接件的受剪承载力的计算方法。Liu等[8]对高强螺栓连接钢-预制混凝土组合结构进行了推出试验,提出了摩擦型高强螺栓连接件的抗剪承载力计算公式和剪力-滑移本构关系。刘中良等[9]对预制装配式高强螺栓抗剪连接件的抗剪性能进行了研究,并与现浇混凝土板推出试件的破坏模式和受力性能进行对比,结果表明螺栓直径,孔径比等对螺栓极限承载有一定影响,并提出了由抗拉强度和截面面积控制的抗剪承载力计算公式。Hosseini等[10]评估了螺栓连接和传统剪力连接件的静态强度和延性,将螺栓剪力连接件的疲劳强度与栓钉进行了比较,并讨论了不同剪力连接件在静态和疲劳载荷作用下的破坏模式。何余良等[11]进行了10个混杂纤维混凝土的推出试件,通过分析纤维、螺栓直径、螺栓孔径比等不同参数来研究螺栓连接件的抗剪性能。蔡莉莉等[12]进行了装配式剪力群钉推出破坏试验,研究了装配式剪力群钉的变形、滑移、裂缝发展以及栓钉破坏等典型破坏特征,并结合数值方法分析了栓钉与混凝土的相互作用关系。Ataei等[13]通过12个推出试验,研究了螺栓尺寸、混凝土强度、螺栓强度以及预制混凝土板螺栓孔和螺栓之间间隙量等参数对螺栓连接件抗剪承载力的影响。结果表明混凝土压碎、钢梁翼缘变形和剪力连接件的断裂为试件失效后的主要破坏损伤形式。

综上所述,前人研究多集中在推出试验得到的螺栓抗剪连接性能,对栓接组合梁的研究较少,分析尚不充分。鉴于此,选用摩擦型高强螺栓作为组合梁的剪力连接件,基于ABAQUS有限元软件建立数值模型,在验证试验结果的基础上,对螺栓抗剪性能和组合梁抗弯性能开展参数化分析,为今后的试验研究及工程应用提供参考。

1 推出试验数值模型

1.1 模型尺寸、单元与网格

参考文献[4]对6组推出试件进行的静力试验,试件尺寸如图1[4]所示。试件由一个H250 mm(高度)×250 mm(宽度)×9 mm(腹板厚度)×14 mm(翼板厚度)型钢梁和2块460 mm(长)×400 mm(宽)×120 mm(高)的预制混凝土板组成,钢梁和混凝土板预留螺栓孔,混凝土板通过两个高强螺栓与钢梁相连接。

图1 推出模型尺寸[4]Fig.1 Details of push-out specimen[4]

按照试验模型建立数值模型,组成构件包括混凝土板、钢梁、高强螺栓、垫圈,钢筋和刚性底板。考虑到推出试验的对称性,利用ABAQUS软件建立1/4数值模型。其中混凝土板、钢梁、螺栓、垫片均采用8节点三维实体线性减缩积分单元(C3D8R),钢筋采用2节点三维桁架单元(T3D2)。钢梁的尺寸划分为三级,全局网格尺寸为10 mm,螺栓孔周边局部区域尺寸为6 mm,螺栓孔最内侧沿周向尺寸为4 mm;垫圈、钢筋和刚性底板采用全局布种的方式,网格尺寸分别为4、20、50 mm;混凝土板网格的全局尺寸为5 mm,螺栓孔最内侧沿周向尺寸为2.5 mm;螺栓采用全局布种,网格尺寸为2.5 mm。模型网格如图2(a)所示。

1.2 接触、约束与边界条件

装配过程中钢梁-混凝土板、垫片-混凝土板、垫片-螺栓、混凝土板-刚性底板等接触约束均采用“表面-表面”相互作用,在其法线方向和切线方向分别使用“硬”接触和“罚”函数接触,钢-混凝土界面的摩擦系数取为0.45[14],钢-钢界面的摩擦系数取Lee等[15]所建议的0.5。在忽略滑移和黏结的情况下,钢筋和混凝土板之间应用了嵌入约束。

为匹配试验条件,在刚性底板底面中心施加固定约束。对1/4模型施加边界条件,分别对面1设置x、z向对称边界条件,面2设置z向对称边界条件,面3设置固定边界条件,钢筋和混凝土板之间设置“嵌固”约束。钢梁顶面进行“耦合”约束至参考点,如图2(b)中所示。

1.3 荷载步与失效准则

数值分析采用隐式静态分析,Newton-Raphson法逐级迭代位移控制荷载,分析步骤如下。

步骤1通过螺栓荷载(Bolt Load)选项将预紧力施加到螺栓上。

步骤2通过与钢梁顶部“耦合”的参考点施加竖直向下的位移荷载,同时将螺栓设置为固定在当前长度,以模拟持续不变预紧力。

与试验破坏模式相似,混凝土损伤和应变达到极限值表征混凝土板开裂,螺栓全截面进入塑性表征螺栓断裂,均可判断模型失效。

1.4 材料本构关系

1.4.1 混凝土

混凝土采用ABAQUS材料模型库中的塑性损伤(concrete damaged plasticity, CDP)模型。基于Hognestad模型,普通混凝土的压缩应力-应变曲线可以简化为三部分。弹性阶段和非线性阶段根据式(1)、式(2)计算。考虑到三轴应力状态,下降阶段被简化为直线,如图3(a)所示。

Ec为混凝土弹性模量;f′c为抗压极限强度的0.85倍;εco为混凝土压缩应力-应变曲线图中峰值应变,取值为0.002;εcu为混凝土压缩应力-应变曲线图中极限应变,取值为0.01;ft为抗拉极限强度;εto为混凝土拉伸应力-应变曲线图中峰值应变;εtu为混凝土拉伸应力-应变曲线图中极限应变

(1)

Ec=12.4×103+460f′c

(2)

式中:f′c抗压极限强度的0.85倍;εco为峰值应变,取值为0.002;σc为压缩应力;εc为压缩应变。

混凝土的抗拉极限强度取抗压极限强度的0.1倍,拉伸应力-应变曲线简化两段式,如图3(b)所示。材料强度如表1所示。

表1 混凝土材料强度Table 1 Concrete material strength

1.4.2 钢材

钢梁和钢筋均采用ABAQUS中的弹塑性本构模型,结合Prandtl-Reuess塑性流动准则进行模拟,如图4(a)所示,其中,钢梁与钢筋弹性模量Es=200 GPa,钢梁与钢筋屈服应变εst=0.02,钢梁与钢筋极限应变εsu=0.25,泊松比为0.3。

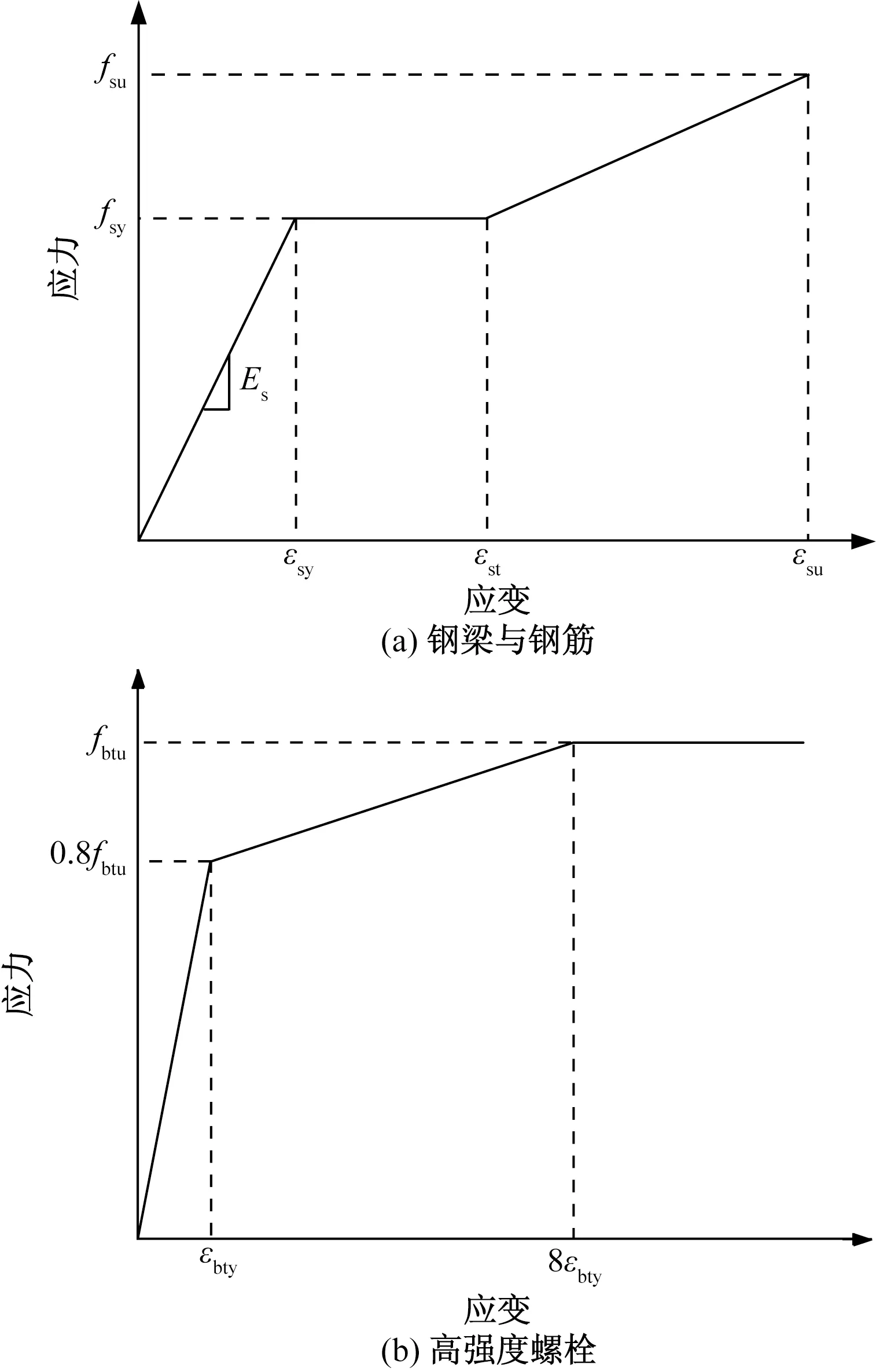
Es为钢筋与钢梁弹性模量;εsy为钢梁与钢筋屈服应变,εst为钢梁与钢筋屈服应变;εsu为钢梁与钢筋极限应变;fbtu为螺栓的极限承载力;0.8fbtu为高强度螺栓屈服应力;εbty为高强度螺栓屈服应变;8εbty为高强度螺栓极限应变

高强螺栓采用三折线本构关系[16],如图4(b)所示,螺栓的断裂应变为0.15[17]。材料强度如表2所示。

表2 钢材材料强度Table 2 Steel material strength

1.5 模型验证

将本文模型计算的荷载-滑移曲线与文献[14]试验得到的荷载-滑移曲线进行对比,如图5所示。可以看出,本文方法能够合理预测钢-混凝土组合结构中高强螺栓连接件的荷载-滑移性能,特别是对抗滑移荷载、峰值荷载、峰值荷载对应的极限滑移值以及承压阶段剪切刚度的预测较为准确。图6为试件破坏形态对比。

s为钢梁与混凝土板界面的相对滑移;V为高强螺栓抗剪承载力

图6 试件破坏形态对比Fig.6 Comparison of failure mode

2 螺栓连接件抗剪性能参数分析

2.1 高强螺栓预拉力

为了分析高强螺栓预拉力(T)的影响,以M20-8.8级高强螺栓为例,保持其余参数与上述模型一致,对模型施加25、50、75、100、125 kN预拉力。所得荷载-滑移曲线如图7所示,预拉力对滑移荷载、极限荷载、极限滑移和承压抗剪刚度的影响如图8所示,其中,滑移荷载(Vs)为钢-混凝土克服摩擦时的荷载,极限抗剪承载力(Vu)为承压阶段的最大承载力,极限滑移(Su)为极限荷载所对应的滑移,承压阶段抗剪刚度(Ks)为荷载-滑移曲线上0.7Vu与承压阶段起始点的割线斜率。

s为钢梁与混凝土板界面的相对滑移;V为高强螺栓抗剪承载力

图8 不同预拉力的螺栓力学性能Fig.8 Bolt mechanical properties with different pretensile

从图8可以看出,随着初始预拉力增大,高强螺栓连接件的摩擦阶段增长,滑移荷载随预拉力呈线性增长,这是由于预拉力使钢-混凝土界面的最大静摩擦力提高。值得注意的是,预拉力对承压阶段力学应能也有一定影响。与25 kN预拉力相比,125 kN预拉力时的螺栓极限承载力受影响较小,仅提高了5.5%,这是因为螺栓破坏时收到剪切和拉伸共同作用,而破坏时的拉应力远超初始预拉力,则不同预拉力的螺栓在破坏时应力状态是相近的;极限滑移和承压抗剪刚度所受影响较大,分别增加了14.6%和20.3%,这得益于摩擦阶段的延长,延缓了螺栓进入非线性承压阶段进程,螺栓在剪切变形较小的情况下进入了破坏软化阶段,拉应变分量得到充分发展。因此,在实际工程中应尽量按照规范足额施加螺栓预拉力。

2.2 混凝土板孔径的影响

以M20-8.8级高强螺栓和125 kN预拉力的模型为例,将混凝土板孔径D分别改变为24、25、26 mm 3种,结果如图9、图10所示。

s为钢梁与混凝土板界面的相对滑移;V为高强螺栓抗剪承载力

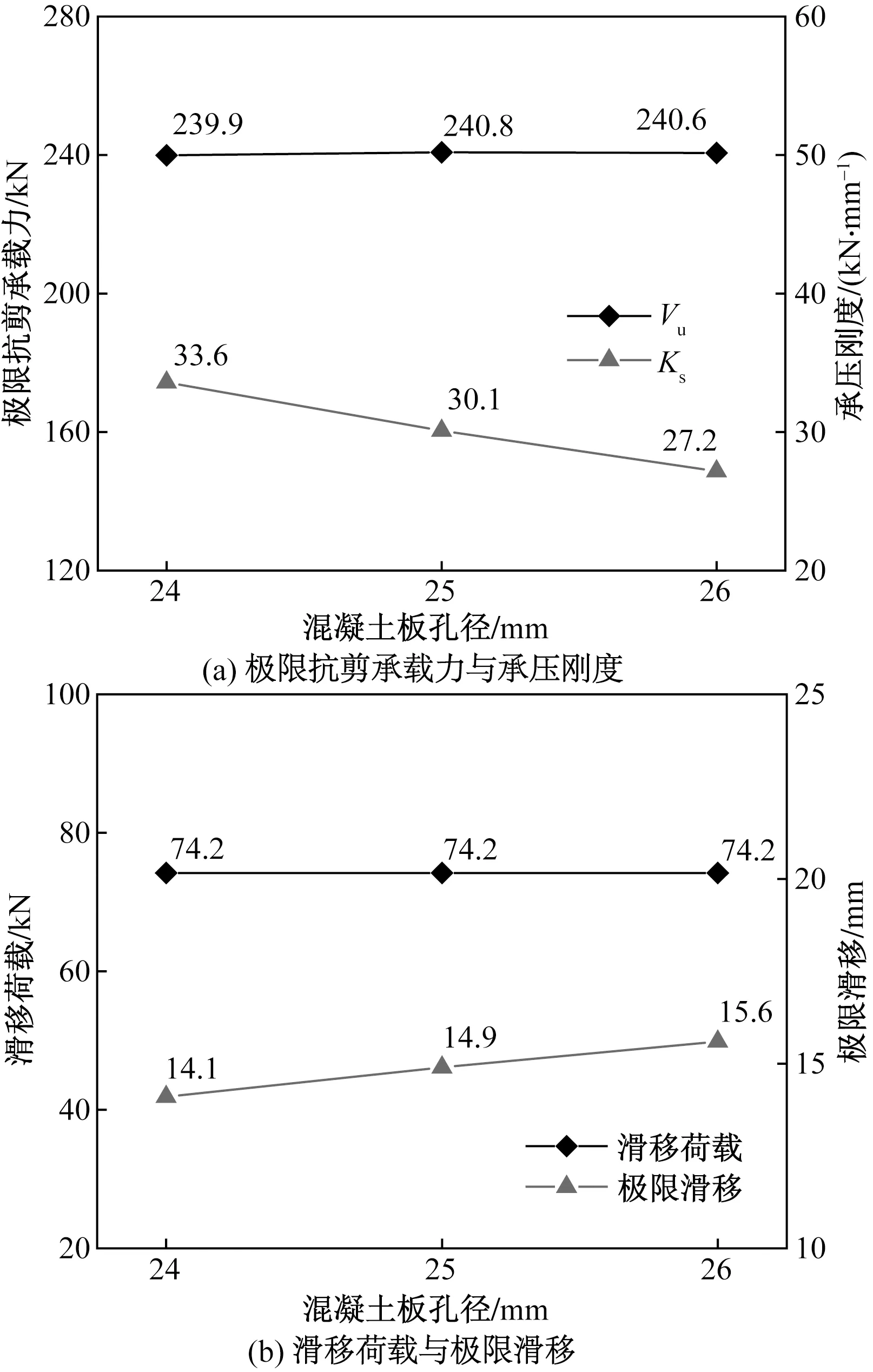
图10 不同混凝土孔径的螺栓力学性能Fig.10 Bolt mechanical properties with different concrete apertures

从图10可以看出,混凝土板孔径的增大对高强螺栓的滑移荷载和极限承载力几乎无影响,而极限滑移的增长值也几乎等于孔径的增大量。当混凝土板孔径从24 mm增加到26 mm时,高强螺栓承压抗剪刚度减小了19.1%,这是由于较大的孔径使得混凝土孔壁与螺栓杆实际接触面积减少,更容易造成混凝土承压变形。因此,从刚度和滑移量的角度考虑,实际工程应提高制孔精度,减小孔径,必要时用灌浆料填充。

2.3 混凝土强度的影响

以M20-8.8级高强螺栓、125 kN预拉力的模型为例,取C30、C40、C50、C60混凝土强度,分析混凝土强度对连接件力学性能的影响。图11、图12为不同混凝土强度下的荷载-滑移曲线及其影响规律。

图12 不同混凝土强度下的力学性能Fig.12 Bolt mechanical properties with different concrete strength diameters

从图11可以看出,不同混凝土强度的荷载-滑移曲线在摩擦阶段和滑移阶段基本重合,在进入承压阶段后产生了明显区别。当混凝土强度从C30提高到C60时,螺栓连接件的极限承载力、极限滑移和承压抗剪刚度都明显提高。其中极限承载力提高了29.3%,极限滑移提高了近一倍,承压抗剪刚度也略有增加,提高了11.2%。这是由于混凝土强度较低时,螺栓孔周围的混凝土容易发生局部压碎破坏,无法在剪切面给螺栓提供可靠支撑,导致螺栓的强度和延性无法完全发挥。因此,在实际工程中,应当适当提高混凝土强度以充分发挥高强螺栓连接件的承载能力。

2.4 螺栓抗拉强度

为了分析螺栓抗拉强度fu对高强螺栓连接件力学性能的影响,以M20、125 kN预拉力的高强螺栓为例,选用抗拉强度分别为800、900、1 000、1 200 MPa,图13、图14为不同抗拉强度螺栓的分析结果。

s为钢梁与混凝土板界面的相对滑移;V为高强螺栓抗剪承载力

图14 不同抗拉强度的螺栓力学性能Fig.14 Bolt mechanical properties with different bolt strength strength

若预拉力相同,则螺栓强度等级的提高对摩擦阶段与滑移阶段的力学性能基本无影响,但承压阶段和破坏阶段的承压抗剪刚度、极限承载力和极限滑移均有明显提高。其中,承压抗剪刚度提高了11.1%,极限承载力提高了36.1%,极限滑移提高了27.5%。因此,若不改变预拉力,且工程设计仅利用摩擦阶段,则无需提高螺栓强度等级;若按承压型高强螺栓设计,利用承压阶段强度,则可使用更高强度的螺栓。

3 简支组合梁数值模拟及参数分析

3.1 数值模型

推出试验能较好地反映连接件的抗剪性能,但无法体现组合梁的整体受弯性能。因此,用上述相同的建模方法建立了简支组合梁的数值模型,根据图15所示的钢-混凝土组合梁尺寸简图建立模型。模型全长5 300 mm,计算跨度为5 000 mm,其中纯弯段1 150 mm,剪跨段2 700 mm。钢梁采用HW300 mm(腹板宽度)×200 mm(翼板宽度)×8 mm(腹板厚度)×12 mm(翼板厚度)截面,屈服强度355 MPa,混凝土板厚度为100 mm,混凝土强度为C40。分析采用10.9级高强螺栓作为抗剪连接件,螺栓双排布置,螺栓横向间距为100 mm。混凝土预留螺栓孔直径比螺栓直径大4 mm,钢梁上翼缘预留螺栓孔直径比螺栓直径大2 mm。

图15 钢-混凝土组合梁尺寸Fig.15 Details of Steel-concrete composite beam dimensions

由于构件本身和加载条件具有对称性,为节省计算成本、提升分析效率,对组合梁模型的建立进行适当的简化,仅建立1/4组合梁模型。对称面1限制x方向的平动和绕y、z轴的旋转;对称面2限制z方向的平动和绕x、y轴的旋转;对支座处限制x、y方向的平动和绕y、z轴的旋转。模型的网格及接触条件与推出模型一致,如图16所示。

图16 组合梁模型边界条件Fig.16 Boundary conditions of compsite beam model

数值模拟均采用隐式分析,分为两个分析步进行:①通过对螺栓施加螺栓荷载(BOLT LOAD),将预紧力施加到螺栓上;②将集中荷载施加在1/3跨处的参考点上,并通过耦合作用将荷载传递至混凝土板,同时将螺栓荷载第2个分析步中的荷载方法选择为固定在当前长度。

为在ABAQUS中准确得到组合梁的计算结果,需要确定组合梁的破坏时刻。由于现行规范的对组合梁的设计采用塑性设计,因此将钢梁跨中全截面进入屈服应力作为组合梁破坏的依据。

3.2 参数分析

3.2.1 螺栓预紧力

在以螺栓预紧力为设计参数进行建模与参数化分析时,除螺栓预紧力外,其余参数保持不变,。分别建立螺栓预紧力为90、110、130、150、170 kN的5个组合梁模型进行参数分析,荷载-位移曲线及荷载-滑移曲线如图17所示。

由图17可知,当螺栓预紧力从90 kN变化到170 kN时,试件的极限承载力和极限滑移最大仅增加了约1.9%,变化幅度几乎可以忽略。而初始抗弯刚度分别增加了5.2%、6.6%、7.6%、8.8%,滑移荷载分别明显增加了19.9%、39.8%、59.6%、75.9%,极限滑移分别减少了2.2%、3.7%、9.2%、7.3%,这表明更大的螺栓预紧力使钢-混凝土界面最大静摩擦力增大,延缓纵向滑移发展过程,增强组合作用,表现出更好的刚度。值得注意的是,当预紧力为170 kN时,极限滑移较150 kN时增大,这是由于提高螺栓预紧力时会导致螺栓孔附近混凝土局部压力增加,进而导致混凝土产生局部损伤。因此在实际工程中,对刚度有要求的组合梁可以通过增加螺栓预紧力来达到设计目标,但螺栓预紧力上限值应根据混凝土标号进行合理设置,不可过大。

3.2.2 混凝土强度

保持剪力连接程度为100%不变,螺栓直径均为M20,选取4种常见混凝土强度,分别建立混凝土强度为C30、C40、C50、C60的5个组合梁模型进行参数分析,所得结果如图18所示。

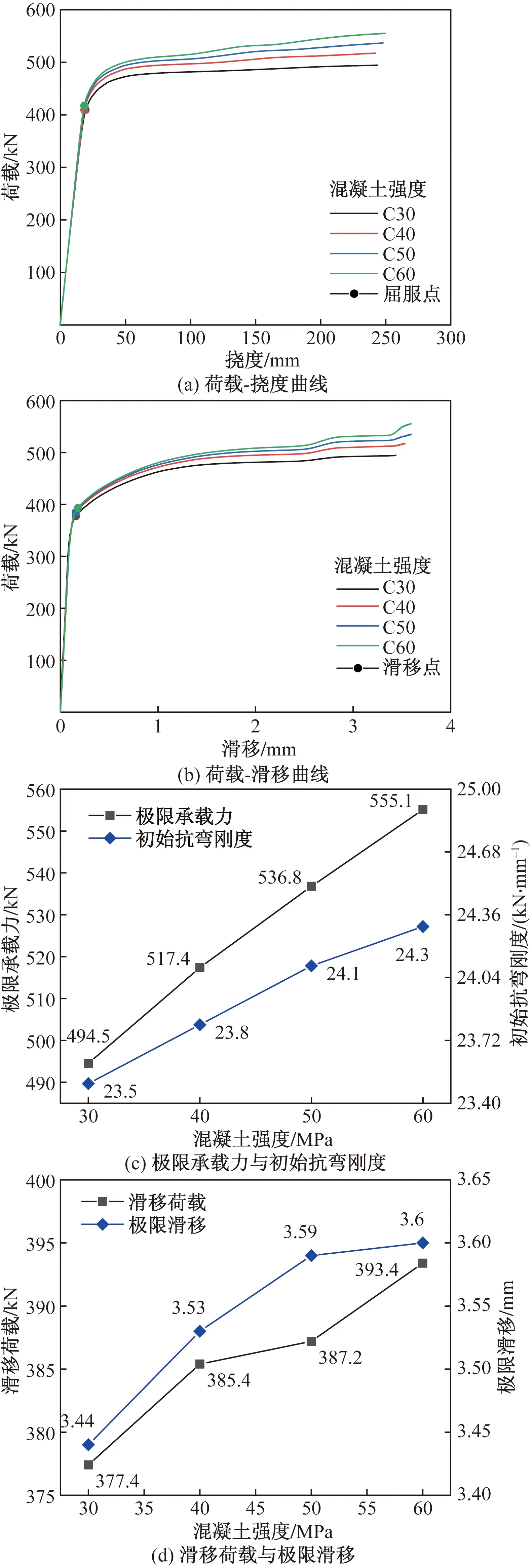
图18 不同混凝土强度的组合梁力学性能Fig.18 Mechanical properties of composite beas with different concrete strength

由图18可知,当混凝土强度从C30增大至C60时,组合梁的极限承载力分别增加了4.6%、8.7%、12.3%,但增长幅度逐渐较小;得益于混凝土本身的弹性模量增加,组合梁的初始抗弯刚度有少许提升,分别增加了1.4%、2.4%、3.5%。随着混凝土强度增大,组合梁滑移荷载分别提高了2.1%、2.6%、4.3%,这是因为较大的混凝土强度提高了组合界面的中性轴高度,则相同外荷载下钢-混凝土界面的纵向剪力减小。

3.2.3 螺栓等级

在以螺栓等级为设计参数进行参数化分析时,通过改变螺栓个数的方法保证剪力连接程度为100%,分别以8.8级、9.8级、10.9级、12.9级4种类型的螺栓建立组合梁模型,螺栓直径均为M20。所得结果如图19所示。

以“100%-9.8”为例,表示保证剪力连接程度为100%,以9.8级螺栓建立的组合梁模型

由图19可知,当螺栓等级从8.8级变化到12.9级时,试件的极限承载力略有下降,最大降幅为0.7%,初始抗弯刚度最大降低2.6%,这是因为保证直径与抗剪连接程度不变的情况下,增大螺栓等级导致螺栓个数减少,刚度分布更加不均匀,但该影响较为微小。组合梁的极限挠度分别增加了2.2%、11.2%、16.2%,极限滑移分别增加了18.6%、20.2%、29.2%。螺栓等级和滑移荷载呈负相关,随着螺栓等级增大,克服摩擦所需的荷载分别降低了5.0%、17.5%、24.1%,这是因为螺栓等级越高,其排列间距越大,根据圣维南原理可知摩擦力主要存在于螺栓周围,则摩擦力分布不均导致滑移荷载降低。在实际工程中,对滑移不敏感的结构可以采用增大螺栓等级的方法提高施工效率,但对滑移要求较高的结构则应选择低等级螺栓来保证抗剪刚度在钢-混凝土界面上的近似均匀离散。

4 结论

以螺栓连接的钢-混凝土组合梁为研究对象,采用有限元数值分析方法,在对已有试验验证的基础上对钢-混凝土组合梁的静力性能及高强螺栓的力学性能展开研究,得到以下结论。

(1)所建立的数值模型与推出试验吻合良好,钢-混凝土连接的破坏模式均为高强螺栓剪断,高强螺栓受力过程分为4个阶段:滑移前的正常使用阶段(包括摩擦传力阶段和滑移阶段)、承压阶段和破坏阶段。

(2)螺栓预拉力、混凝土强度的增大有利于提高螺栓极限承载力和承压抗剪刚度,其中混凝土强度对承载力的影响较大,螺栓预拉力对承压抗剪刚度较大。混凝土孔隙对螺栓承载力几乎无影响,但显著影响螺栓刚度。在工程中提高混凝土强度不仅提高螺栓的性能,还可保证预紧力的足额施加。

(3)在栓接组合梁中,提高螺栓预紧力可增大钢-混凝土界面的摩擦力,而更高的混凝土强度可以使组合截面的中性轴上移,这都增强了钢和混凝土部件的组合作用,进而提高抗弯刚度、降低截面滑移。相反,在保证抗剪连接程度不变的情况下,提高螺栓等级导致界面刚度分布不均,不利于滑移控制。