基于旗鱼优化算法的电力系统动态经济调度方法研究

李国全,李玲玲

(1. 开滦能源化工股份有限公司,河北 唐山 063018;2. 河北工业大学,天津 300401 )

0 引言

过去几十年,电力系统已经发生了巨大变化,包括可再生能源的迅速增长、分布式发电资源的广泛部署、智能电网技术的快速发展等[1,2]。这些变化为电力系统的运行和管理带来了新的机遇和挑战。传统的电力系统调度方法可能无法有效应对这些挑战,相比于静态经济调度,动态经济调度能够充分调整电力系统中的用电单位、提升资源利用率、降低电力系统运行成本,是提高电力系统经济效益和环境效益的关键技术,其运行和管理直接关系到能源效率、可持续性、经济性和供电可靠性等重要问题。因此,对电力系统的动态经济调度方法进行深入研究,对于解决当前和未来电力行业面临的诸多挑战至关重要。

动态经济调度方法旨在实现电力系统的最优运行,以降低成本、提高能源效率、减少碳排放,并确保供电的可靠性。这涉及复杂的决策问题,需要综合考虑各种因素,如电力市场条件、负荷需求、发电资源可用性、电力网络的稳定性等。

当前,针对不同类型的电力系统经济调度问题,电力行业学者通常使用智能算法或者改进算法[3～5]来提高求解电力系统经济调度问题的速度和解的质量。文献[6]在传统DED模型的基础上,根据机组运行最小平均煤耗成本,建立了考虑机组最优排序的电力系统动态经济调度模型(UOS-DED),进一步降低电力系统动态经济调度成本。文献[7]针对含风电场电力系统动态经济调度问题提出一种基于镜像变换和动态坐标变换的状态转移算法,并使用一种新型的处理约束的修复方法配合罚函数对约束条件进行处理。文献[8]提出基于生成对抗模仿学习的动态经济调度模型,解决调度部门如何安排适应新能源出力不确定性的调度问题。文献[9]提出了一种日前市场考虑需求响应的低碳动态两阶段优化调度方法,并以改进的IEEE 14节点为例对系统碳排放量和总运行成本进行计算分析,验证了该方法可行性和合理性。

为进一步完善电力系统经济调度问题的研究。本文首先建立了动态经济调度的数学模型,确定了在考虑风电情况下,动态经济调度的约束条件和最终目标函数。然后,研究了旗鱼算法的原理,在考虑风电的情况下,利用旗鱼算法对5台火电机组的测试系统进行了动态经济调度。证明了基于旗鱼算法的动态经济调度不仅符合各种约束,而且有着更低的燃料成本和污染排放,表明旗鱼算法能有效处理动态经济调度问题。

本文旨在探讨动态经济调度方法的最新研究进展,分析其在电力系统优化中的应用,为电力系统的可持续发展和创新提供有力支持。电力系统动态经济调度方法的研究有助于实现清洁、可持续和高效的电力供应。

1 电力系统动态经济调度模型

1.1 目标函数

动态经济调度的主要目标是在考虑不同约束的情况下追求燃料成本和污染排放的最小化。本研究利用系数w将多目标函数转化为单目标函数,在考虑风电的情况下,目标函数见式(1)。

FE=wFue+H(1-w)Emm

(1)

式中,FE为待优化函数;Fue为燃料成本函数;Emm为污染物排放总量;H为w=0时的价格惩罚因子[10]。

w的值是影响目标函数对燃料成本和污染排放量的重点。w值越接近1,目标函数越关注燃料成本;w值越接近0,则目标函数越关注污染物排放量。当w=1时,问题转化为动态经济调度问题[11];当w=0时,则问题转化为动态排放调度问题。

1.1.1 燃料成本函数

考虑阀点效应[12]的DED问题的燃料成本函数为二次函数和正弦函数之和,见式(2)。

(2)

式中,f1为单个调度周期的燃料成本;T为24个调度周期;N为火电机组个数。νi、ηi、γi、θi和ρi为机组i的燃料成本系数,Pi,t为第t个调度周期内机组i的输出功率。

1.1.2 污染排放函数

污染物包括SOx、NOx等。本研究采用污染气体综合模型[13],函数见式(3)。

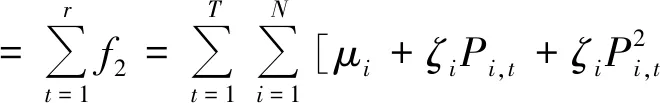
+φiexp(χiPi,t)]

(3)

式中,f2为系统单个调度周期内的污染物排放量;μi、ζi、ζi、φi和χi为机组i的污染物排放系数。

1.2 约束条件

1.2.1 功率平衡约束

功率平衡约束[14]见式(4)。

(4)

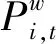
(5)

式中,Lij、Li0、L00为网络损耗系数。

1.2.2 机组输出功率约束

机组输出功率约束[16]见式(6)。

(6)

式中,Pi,min和Pi,max分别为机组i的最小、最大输出功率。

1.2.3 斜坡率约束

斜坡率约束见式(7)。

(7)

式中,PURi和PDRi为相邻周期间机组i上行调节功率和下行调节功率的最大值和最小值。

1.3 动态经济调度综合模型

将式(1)到式(7)相结合,得到动态经济调度问题的总体目标函数如式(8)所示:

(8)

式中,A为功率平衡约束;B为机组输出功率约束;C为斜坡率约束。

1.4 折中方案的选择

对于动态经济调度问题,通过建立隶属度函数来评价不同目标下获得结果的满意度。将式(8)中的系数w从0增加到1,步长区间为0.05。每个增量中得到的结果被保留,形成一个帕累托解集[17]。折中解由隶属度函数决定。具体步骤如下:

(1) 计算帕累托解集中各解的满意度,见式(9)。

(9)

式中,δk,l为第l个解对第k个目标的满意度;fkmax和fkmin表示帕累托解集中第k个目标的上下限。

(2) 计算每个解决方案的总体满意度:

(10)

式中,n是目标数。由于本研究考虑了燃料成本和污染物排放两个目标,所以n被设置为2。J是帕累托解集中的解的个数。

(3) 最终,选择δl最大的方案作为折中方案。

2 旗鱼算法的原理

2.1 旗鱼的位置更新

旗鱼算法(The Sailfish Optimizer, SFO)的主要灵感来自于旗鱼群体狩猎的攻击交替策略。并在此基础上建立了一种优化算法[18]。

SFO算法参考了旗鱼在群体狩猎时的交替攻击策略,每个旗鱼个体代表一个候选解,旗鱼的位置更新用式(11)表示。

(11)

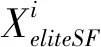
λi=2*rand(0,1)*PD-PD

(12)

(13)

式中,NSF,NS分别代表旗鱼和沙丁鱼的数量。

2.2 沙丁鱼的位置更新

每条沙丁鱼都必须根据旗鱼当前的最佳位置和每次迭代时的攻击能力更新自己的位置。算法中,沙丁鱼的位置更新见式(14)。

(14)

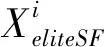
AP=A*(1-2*Itr*e)

(15)

式中,参数A,e控制控制攻击力度的变换,使A线性变换到0。

部分位置的范围定义见式(16)、(17)。

α=NS*AP

(16)

β=di*AP

(17)

式中,参数α是要更新沙丁鱼的数量;β是要更新的维度数量。

2.3 综合考虑旗鱼和沙丁鱼的位置

在捕猎的最后阶段,受伤的沙丁鱼从鱼群中挣脱出来,很快就会被捕获。在该算法中,假设沙丁鱼的位置优于旗鱼,则在这种情况下,旗鱼的位置会与被捕食的沙丁鱼的最新位置替代,从而增加捕食新猎物的机会,见式(18)。

(18)

算法流程如下:

Step1.初始化种群和参数。

Step2.计算旗鱼和沙丁鱼的适应度值,并标记其最优值和位置。

Step3.更新旗鱼,沙丁鱼位置,计算α , β的值。如果攻击力度小于0.5,则更新部分沙丁鱼位置。否则,全部更新沙丁鱼位置。

Step4.沙丁鱼,旗鱼位置替换。

Step5.计算所有适应度值,并更新最优值和位置。

Step6.判断是否满足终止条件,若满足则算法输出结果,否则重复Step2～Step6;

算法流程图如图1所示:

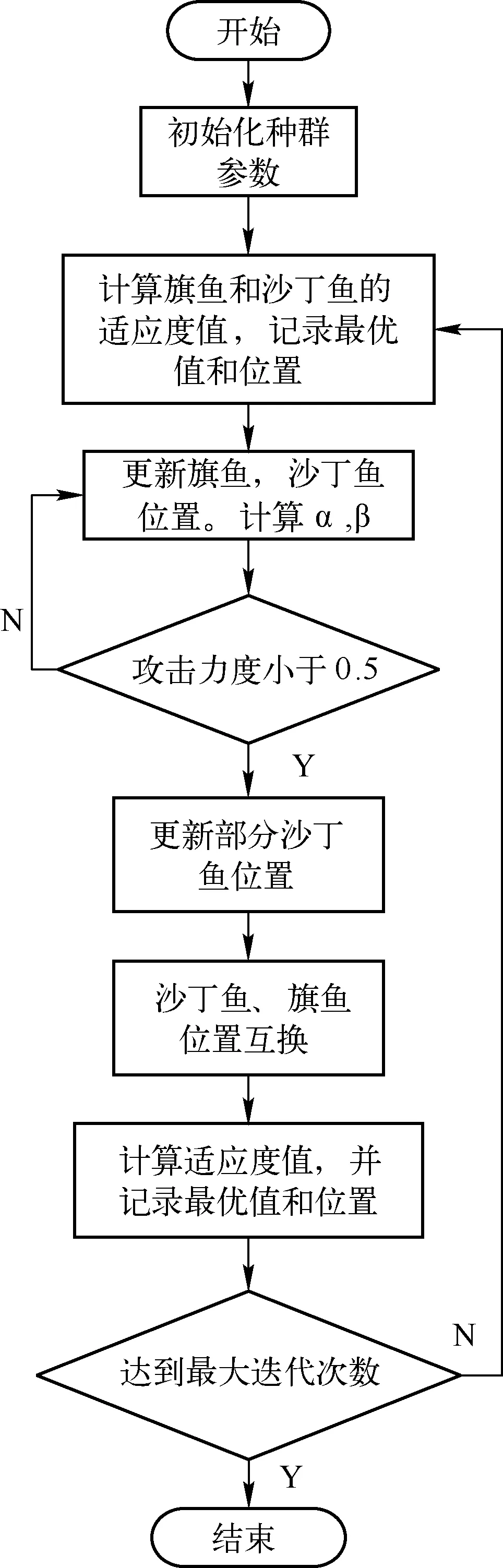
图1 旗鱼算法流程图

3 基于旗鱼算法的动态经济调度

3.1 动态经济调度初始参数

本文将旗鱼算法应用于一个五台火电机组问题以验证其性能。在整体系统考虑风电的情况下[19],每个测试火电机组系统还需要考虑了传输损耗和坡度速率约束[20-22]。程序将在相应的测试系统中独立运行50次,并通过分析参数,将其与PSO算法、进化算法(EP)进行对比来验证SFO的性能。

初试数据设置如下:

旗鱼算法参数的最大迭代次数设置为1000,搜索代理设置为100。机组数据设置见表1,燃料费用系数见表2,污染系统排放量系数见表3;整体测试系统的负荷曲线如图2所示。

表1 机组数据

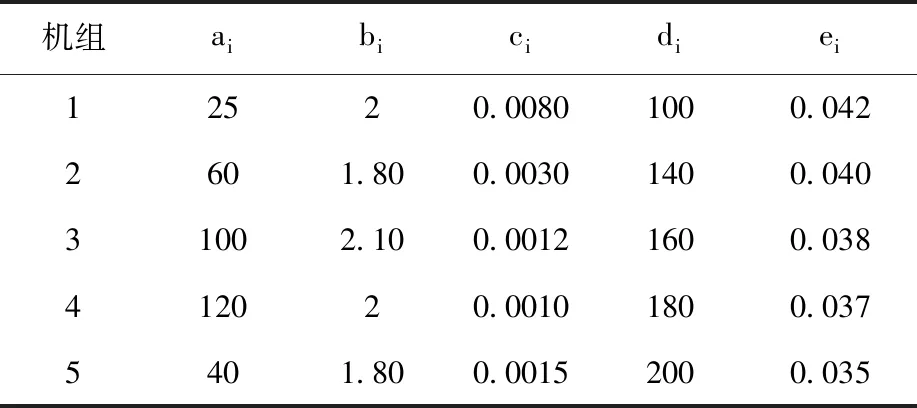
表2 燃料费用系数

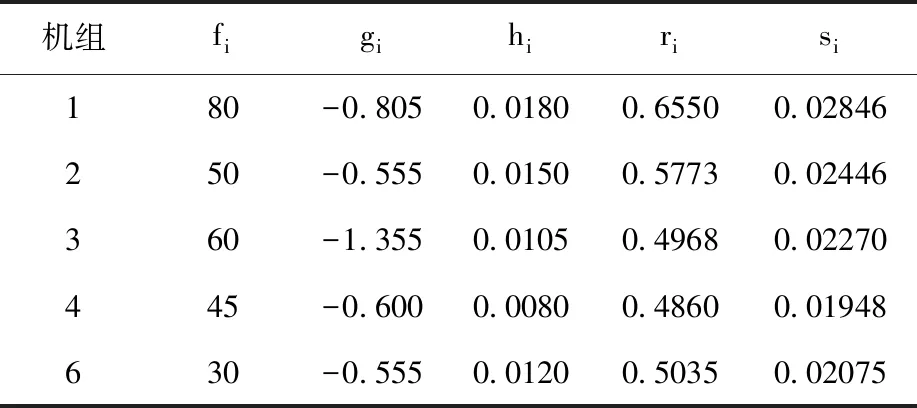
表3 污染系统排放量系数

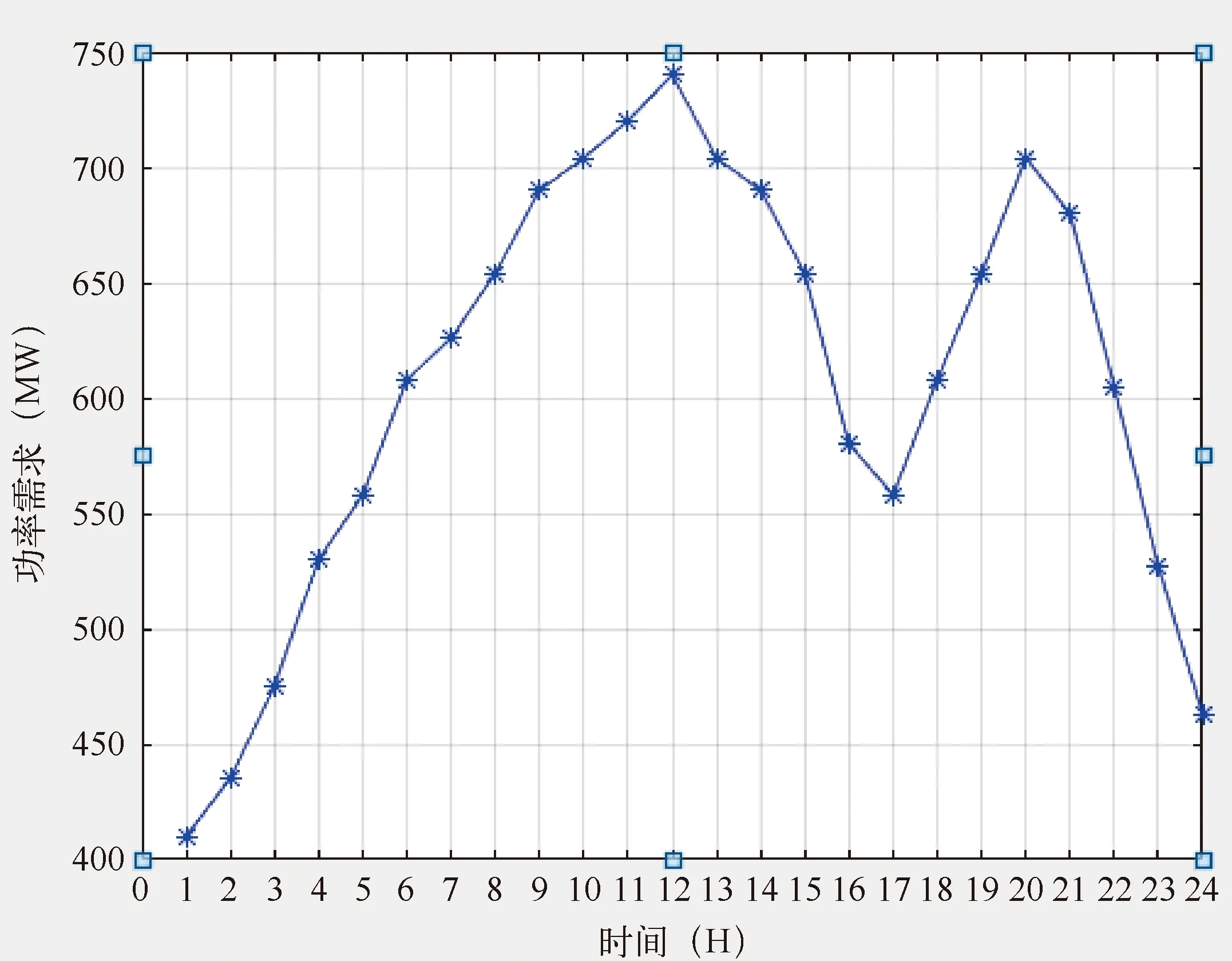
图2 测试系统负荷曲线

3.2 动态经济调度结果分析

将以上数据代入基于旗鱼算法的动态经济调度程序,在考虑风电的情况下运行50次,污染排放与燃料成本见表4。

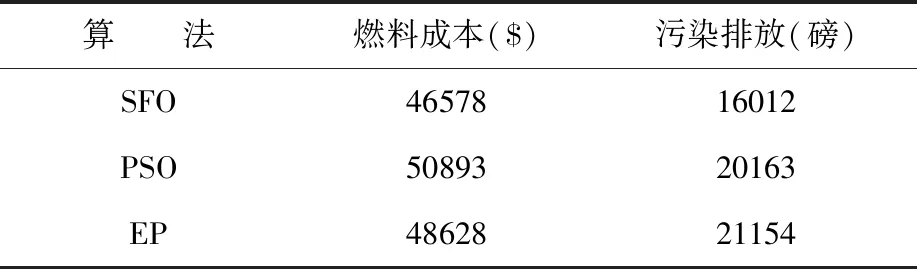
表4 考虑风电情况下污染排放与燃料成本

同时,表4将旗鱼算法的燃料成本与污染排放与PSO算法、EP算法进行对比,不难看出,基于旗鱼算法的动态经济调度得到的燃料成本分别是基于粒子群算法(PSO)的动态经济调度和基于进化算法的动态经济调度的91.52%和95.78%,其污染排放量也分别为后两者的79.41%和75.69%。通过以上分析,表明对于5台火电机组测试系统,应用旗鱼算法有燃料成本、低污染、排放少等优点,运用旗鱼算法进行动态经济调度,可以提高电力系统的经济性和环保性,有利于能源系统可持续发展。

图3为旗鱼算法在求最优解时的收敛曲线,该曲线表明SFO算法在迭代到第683代后产生最优值,这说明旗鱼算法能在迭代周期内很快找到最优解,也证明了旗鱼算法的全局搜索能力和收敛特性。

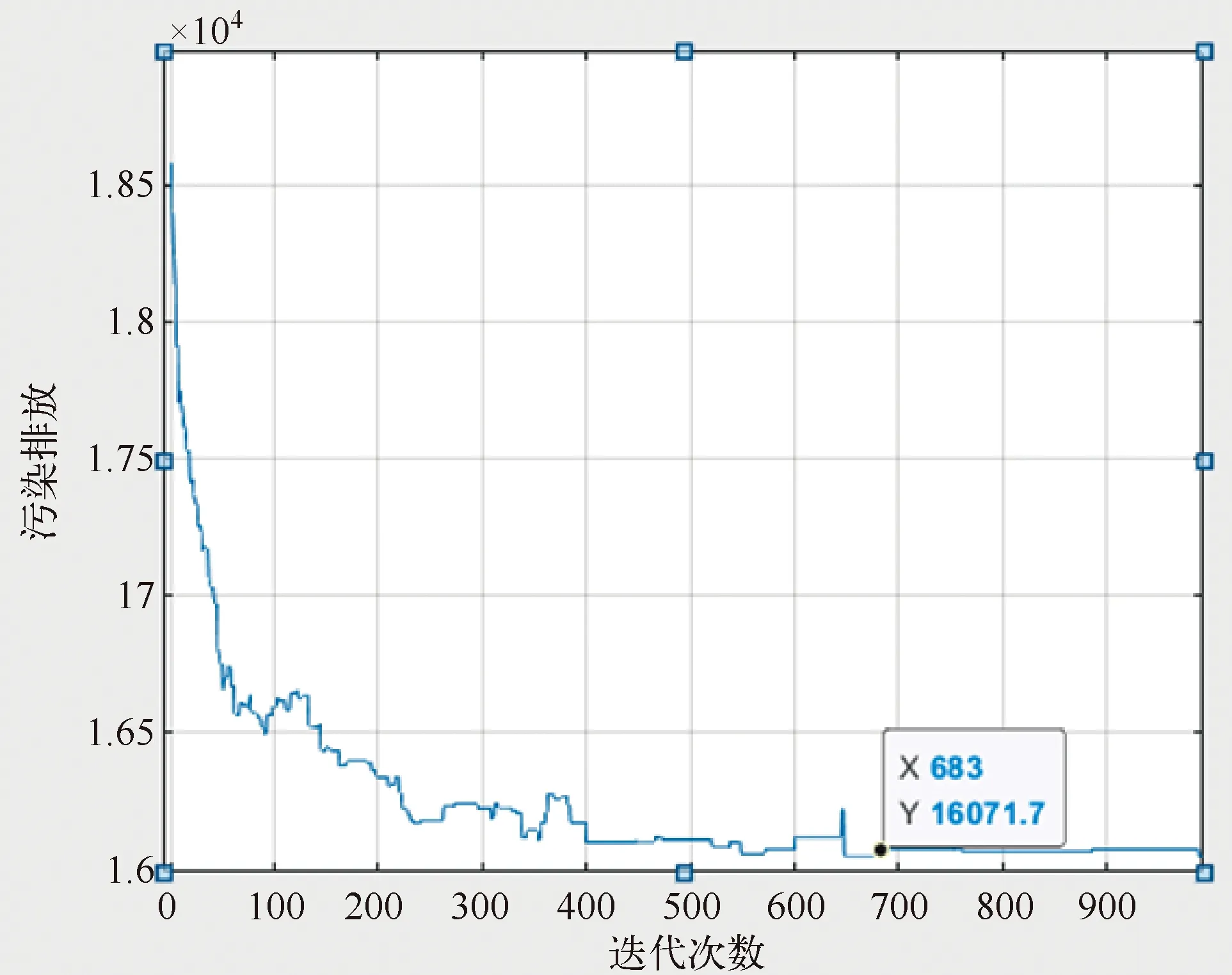
图3 求解测试系统时SFO算法迭代曲线

表5显示了基于旗鱼算法的动态经济调度在求得折中解时,每个调度周期内各机组的详细输出功率及网损等参数。给出了旗鱼算法在考虑风电情况下求解5台火电机组系统时的折中解,通过理论分析,不难发现,各周期内所有机组的输出功率均满足机组输出功率约束。而且,机组各调度周期之间的输出功率也满足了斜坡率约束。同时,表5也显示,各机组的总输出功率之和等于负载需求和网络损耗的总和,这表明基于旗鱼算法的动态经济调度完全符合功率平衡约束。此外,1、2、3号机组的输出功率相对稳定,但用于调峰 4、5号机组的输出功率变化较大。

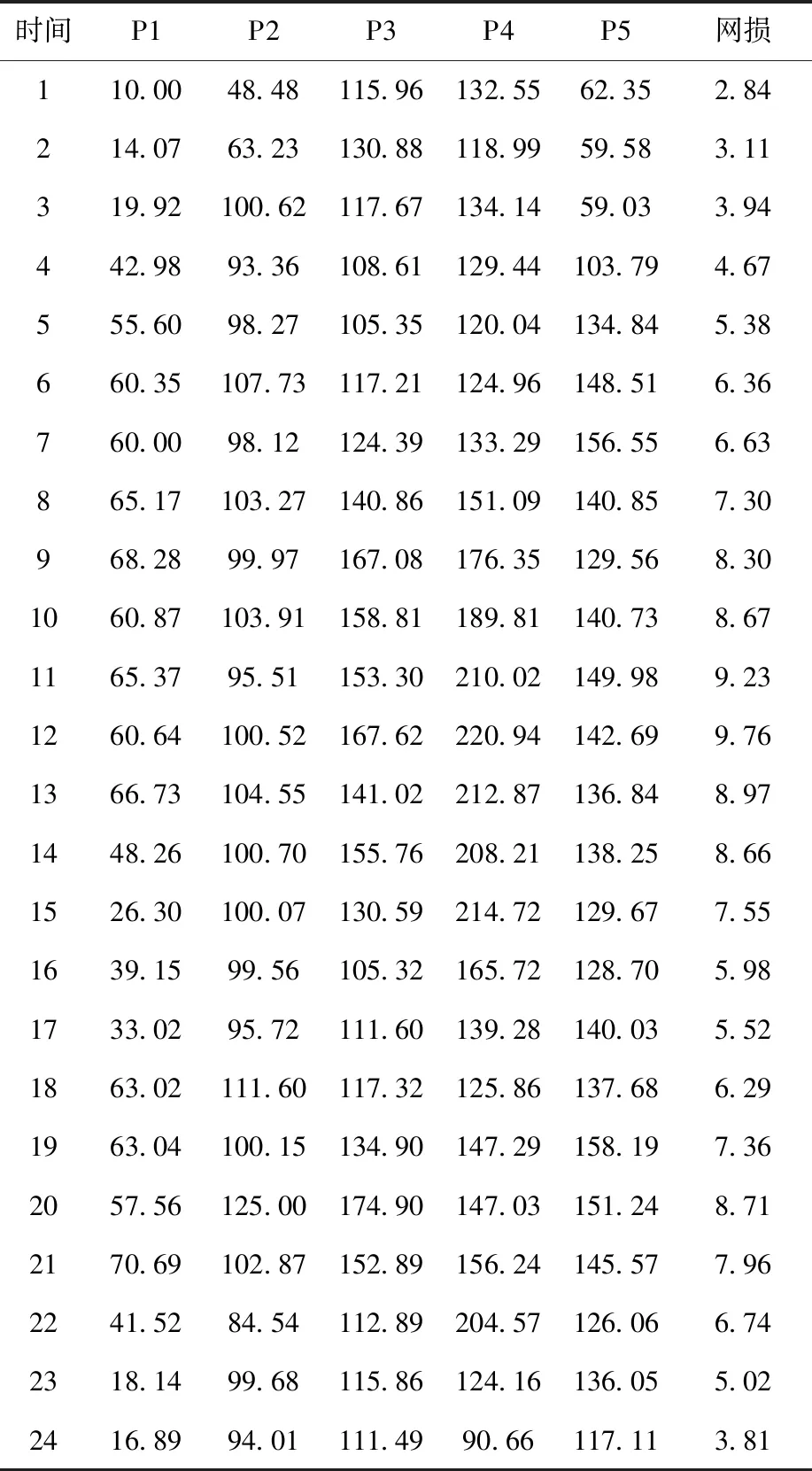
表5 SFO求5台火力发电机组时的小时输出功率、网损 MW

4 结论

(1) 为了进一步证明SFO的有效性,将其应用于一个包含五台机组和双风电的测试系统中。通过实验仿真和深入分析,SFO成功地合理分配了发电机的运行,降低了燃料成本,从而为整个电力系统带来了更大的经济效益。

(2) 研究结果表明,SFO是解决动态经济调度问题的有效工具,可以帮助降低电力系统的燃料成本和污染排放,从而提高电力行业的经济效益。然而,本文仅涵盖了一个特定的测试系统,即五台机组和双风电的情况。下阶段研究可以扩展到更复杂的电力系统,以更全面地评估SFO算法的性能。此外,对于约束条件的处理仍有优化空间,以提高算法的实用性和可扩展性。

(3) 本文未考虑电力系统中的不确定性因素,如天气变化和市场波动,这些因素可能对动态经济调度产生一定影响。下阶段研究可以考虑引入更多可再生能源,如太阳能和潮汐能,以推动电力系统向更清洁和可持续的方向发展。