基于量子遗传模糊推理系统的煤与瓦斯突出预测模型
郭金栋
(淮南职业技术学院 能源工程学院,安徽 淮南 232001)
0 引言
煤与瓦斯突出评价是矿井煤岩动力灾害防控工作的基础,准确预测煤与瓦斯突出及其危险程度已成为矿井安全生产亟待解决的重大问题。随着数据理论和人工智能的快速发展,基于数据驱动的机器学习方法及其应用取得了突破性成果,神经网络[1-2]、支持向量机[3-4]、极限学习机[5]等分类器广泛应用于煤与瓦斯突出灾害的分类识别与预测。神经网络具有较强的非线性映射能力和自学习能力,但其网络结构的确定较为困难,网络结构设计复杂时网络训练容易出现过拟合,网络结构简单又可能导致欠拟合而出现不收敛现象;BP网络采用梯度下降学习算法,容易陷入局部最优,这些问题都影响着BP网络的预测效果。支持向量机解决多分类问题时需要构造多个复合分类器,训练规模较大样本的计算成本较高,且SVM核函数和惩罚参数的合适取值较为困难。极限学习机的参数随机生成导致了结果的随机性,影响预测准确性。为了提高预测准确率和运行效率,不少研究者使用群智能仿生算法优化这些分类器的参数。文献[1]用遗传算法优化BP神经网络的权值和阈值;文献[2]将免疫算法中基于繁殖概率的抗体多样性保持机制引入量子遗传算法,以此对BP网络隐含层数和连接权值进行寻优;文献[3]将等距映射算法与优化加权向量机耦合算法相结合,建立了DDICS-WLS-SVM预测模型,预测精度有所提高;文献[5]提出自适应天牛须算法与极限学习机相结合的预测模型,模型的泛化能力和预测精度效果较好。由于煤与瓦斯突出形成机制的复杂性、机器学习算法本身的弊端以及样本数据特征空间分布的混叠性等问题,煤与瓦斯突出预测的可靠性和准确率并不高,因而非常有必要对煤与瓦斯突出智能预测模型进行深入研究。
自适应神经模糊推理系统(Adaptive Neuro-Fuzzy Inference System,ANFIS)是将神经网络与模糊推理结合在一起的混合系统,ANFIS的模糊推理不依赖于对象模型,系统具有良好的可解释性及强大的学习能力,可以很好地处理非线性问题。ANFIS采用反向传播算法与最小二乘法进行参数调整,学习算法对初始状态及参数非常敏感,在初始解较差或不合理情况下收敛较慢,而且很容易陷入局部极值。本文使用改进的实数编码量子遗传算法改善ANFIS的性能。经典量子遗传算法[2,6-9](Quantum Genetic Algorithm,QGA)用量子位编码表示染色体,量子染色体可以表达多个态的叠加,通过量子位的观测得到二进制编码的染色体,用量子旋转门更新种群,实现对目标问题的优化求解。在求解组合优化问题时,QGA相较传统遗传算法具有更强的全局寻优能力和更快的收敛速度,算法表现出更优良的性能,但QGA不适合求解连续空间数值优化问题[7-9]。为此,不少学者提出了实数编码量子遗传算法(Real-coded Quantum Genetic Algorithm,RQGA),并从理论上分析证明了RQGA算法具有全局收敛性[7-9]。文献[7]提出双链量子遗传算法,该算法利用目标函数的梯度信息计算量子旋转门的旋转角大小,通过构造量子位到实数的映射关系得到实数种群,量子位与实数的映射关系为缩放变化,解码精度不能得到保证,算法仍不可避免地会出现收敛慢和易陷入局部最优等问题。文献[8]通过量子位的观测得到实数编码的染色体,用量子旋转门更新染色体,算法通过模拟量子系统中态叠加性的强不确定性,使算法在迭代过程均有概率搜索整个解空间。RQGA算法可以有效避免经典QGA算法染色体编码转换的问题,减少寻优的计算复杂度,在连续函数的优化中表现出了较好的性能。然而在多峰连续函数的优化中仍然存在搜索速度慢,解的搜索精度相对低,保持种群多样性差,易陷入局部极值等问题。为改善RQGA算法的性能,不少研究者针对文献[7]提出了许多更新策略,但对文献[8]提出的RQGA算法的深入研究相对较少。针对煤与瓦斯突出具体工程问题,本文在文献[8]基础上,提出一种融合多种策略的改进实数编码量子遗传算法(Improved Real-coded Quantum Genetic Algorithm,IRQGA)。IRQGA采用拉丁超立方抽样方法初始化量子种群,加强个体在解空间的均匀化分布;用凸型递减函数对量子旋转门转角大小进行自适应动态调整,增强算法的适应性;借鉴秃鹰搜索算法[10]的阿基米德螺线空间搜索机制对量子染色体进行变异,加强个体与全局最优个体和种群均值之间的信息交流,以此提高寻优能力;用差分变异提升最差个体的进化能力,保持种群多样性;用高斯-柯西变异增强算法跳出局部搜索空间的能力。用量子位的概率幅对一阶Sugeno型模糊推理系统的前件参数和后件参数进行编码,通过IRQGA对模糊推理系统搜寻最优参数,对实例数据进行仿真实验,以平均绝对误差(MAE)均值、均方误差(MSE)均值、均方根误差(RMSE)均值和预测准确率作为评价指标,验证了IRQGA-ANFIS模型的可靠性和准确性,为煤与瓦斯突出预测提供了一种行之有效的方法。
1 煤与瓦斯突出ANFIS预测模型
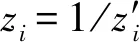
ANFIS结构共分为5层,如图1所示。系统的输入神经元由煤与瓦斯突出的影响因素变量zi(i=1,2,…,5)组成。第1层计算输入分量zi属于各语言变量值模糊集合的隶属度,实现各输入变量值的模糊化处理,本文选用高斯隶属度函数。第2层计算每条规则的触发强度。第3层计算归一化的规则强度。第4层计算每条规则的加权输出。第5层为煤与瓦斯突出危险程度输出。模糊推理系统由前件网络和后件网络两部分组成,系统规则库中的第k个模糊规则可用以下形式表示:

图1 自适应神经模糊推理系统结构示意图
(1)
其中,K为模糊规则总数;pk0,pki(i=1,2,…,5)为结论参数。
模糊规则的获取是ANFIS的关键,模糊规则数过多会导致系统结构复杂,网络易出现过拟合;规则数过少则系统逼近性能不佳。文献[11-12]提出从样本数据直接提取模糊规则的方法,该方法简单易用且无需了解对象内在机制,在一定程度上改善了模糊推理系统的准确性与可靠性。基于数据驱动的模糊规则提取步骤如下:
(1) 第一个输入的样本数据产生一条模糊规则,并定义相应的高斯隶属度函数。图1第一层高斯函数参数的确定方法:将训练样本数据的方差作为高斯函数的宽度,第一个输入样本数据作为模糊子集上的高斯函数的中心。
(2) 将训练样本数据依次进行模糊化,并计算第一条规则的触发强度,若样本数据产生的触发强度之和小于设定的覆盖率阈值,则产生一条新模糊规则,并按步骤(1)在图1第一层创建指定参数的隶属度函数。
(3) 遍历整个样本数据集后,按步骤(1)和(2)得到输入变量在论域上的模糊子集个数。
(4) 根据式(1)的线性表达形式,用最小二乘法求解后件网络参数的初始解。
(5) 用训练样本与测试样本的ANFIS预测性能进行规则筛选,确定最终的ANFIS模糊规则数,即可确定ANFIS网络结构。
用ANFIS预测煤与瓦斯突出的另一个关键问题是寻找最佳的前提参数集和结论参数集,本文采用改进的实数编码量子遗传算法进行寻优。
2 改进实数编码量子遗传算法
2.1 实数编码量子遗传算法
RQGA的量子染色体用量子位的概率幅表示,一条具有m位量子位的染色体编码可表示为
(2)
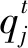
RQGA对染色体的每个量子位概率幅进行测量,以获得一组用二进制表示的确定解,文献[8]将这组确定解用于量子旋转门旋转角的判定,并按式(3)得到求解问题的实数编码染色体。
(3)
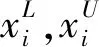
2.2 拉丁超立方抽样初始化种群

2.3 量子旋转角改进策略
量子旋转门的旋转角度通常在0.001π~0.05π范围内取固定值,若旋转角取值较大,量子个体以较快速度聚集,算法容易出现“早熟”现象;若角度较小又会使算法收敛速度太慢甚至出现不收敛情况。为最大程度发掘量子旋转门的寻优能力,本文用式(4)凸型递减函数对旋转角度进行自适应动态调整。
(4)
式中,θmin,θmax分别为0.001π和0.05π;T为最大迭代数。
2.4 阿基米德螺旋线空间搜索机制[10]
RQGA的量子旋转门是以全局最优个体为指导来更新染色体,导致迭代后期种群多样性变差,算法陷入局部极值。文献[7]使用量子非门实现染色体变异,但量子位的两个概率幅简单互换,并不能很好地解决早熟收敛和增加种群多样性。本文借鉴秃鹰搜索算法中秃鹰在俯冲捕获猎物阶段以阿基米德螺旋线方式加速飞向最优位置去捕获食物的策略对量子染色体进行变异,改进策略同时考虑了普通个体与全局最优个体和种群个体均值之间的信息交流。螺旋飞行轨迹采用极坐标数学模型表示,染色体按式(5)~式(12)进行变异更新。
(5)
(6)
(7)
(8)
xr(j)=r(j)×sinh(γ(j))
(9)
yr(j)=r(j)×cosh(γ(j))
(10)
r(j)=γ(j)
(11)
γ(j)=a×π×erand
(12)
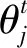
2.5 差分变异策略
差分变异是差分算法中借助种群个体间的差异来对个体进行扰动的操作。最差个体差分变异策略通过追踪种群内最佳个体和全局最优个体进行变异更新,这种变异操作兼顾种群最优个体附近解空间以外区域的搜索,使群体保持较好的多样性,增强勘探能力;进化后期,随着局部搜索能力的不断增强,算法能以更高的精度逼近全局最优解。量子染色体按式(13)进行差分变异。
(13)
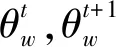
2.6 高斯-柯西变异策略
算法在迭代中后期种群多样性逐渐降低,种群容易被局部极值控制,出现无效搜索。高斯变异和柯西变异是群智能仿生算法常用的变异操作。一维标准柯西分布的概率密度函数与正态分布的密度函数接近,但柯西分布具有较高的两翼概率特性,其分布与水平轴接近时比较平缓,变化速度比高斯分布更慢,且在原点附近的峰值比高斯分布更小,因此高斯变异具有较强的局部发掘能力,而柯西变异具有较强的全局探索能力。为充分发掘种群当前最优个体和全局最优个体的信息,在算法迭代前期,用柯西变异进行大范围搜索,增强算法的全局搜索能力;在算法的中后期,利用高期变异进行局部开发。
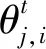
(14)
(15)
式中,η=t/T为变异系数;N(0,δ2)为满足高斯分布的随机数;C(0,δ2)为柯西分布生成的随机数,柯西分布随机变量生成函数为η=tan[(ξ-0.5)π]。
2.7 算法流程
输入:种群规模N、最大迭代次数T、量子染色体长度m,ANFIS待优化参数取值范围等。
输出:最优染色体及其适应度值。
(1) 用拉丁超立方采样方法初始化种群Q。
(2) 按文献[8]对种群实施一次测量得到实数编码染色体,将ANFIS输出的均方误差MSE作为目标函数,计算个体适应度,进行适应度评价,找到并记录最优适应度值和最优染色体。
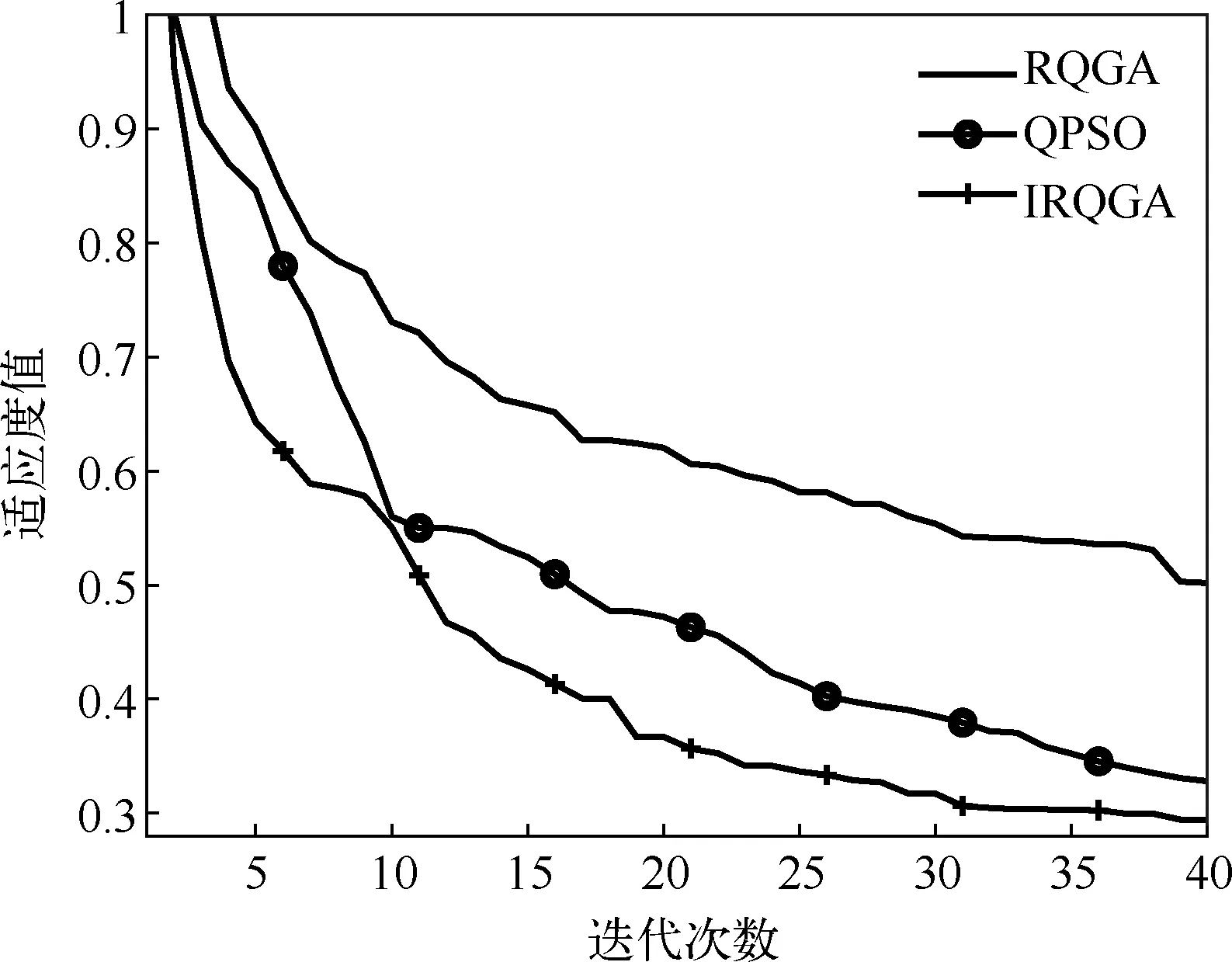
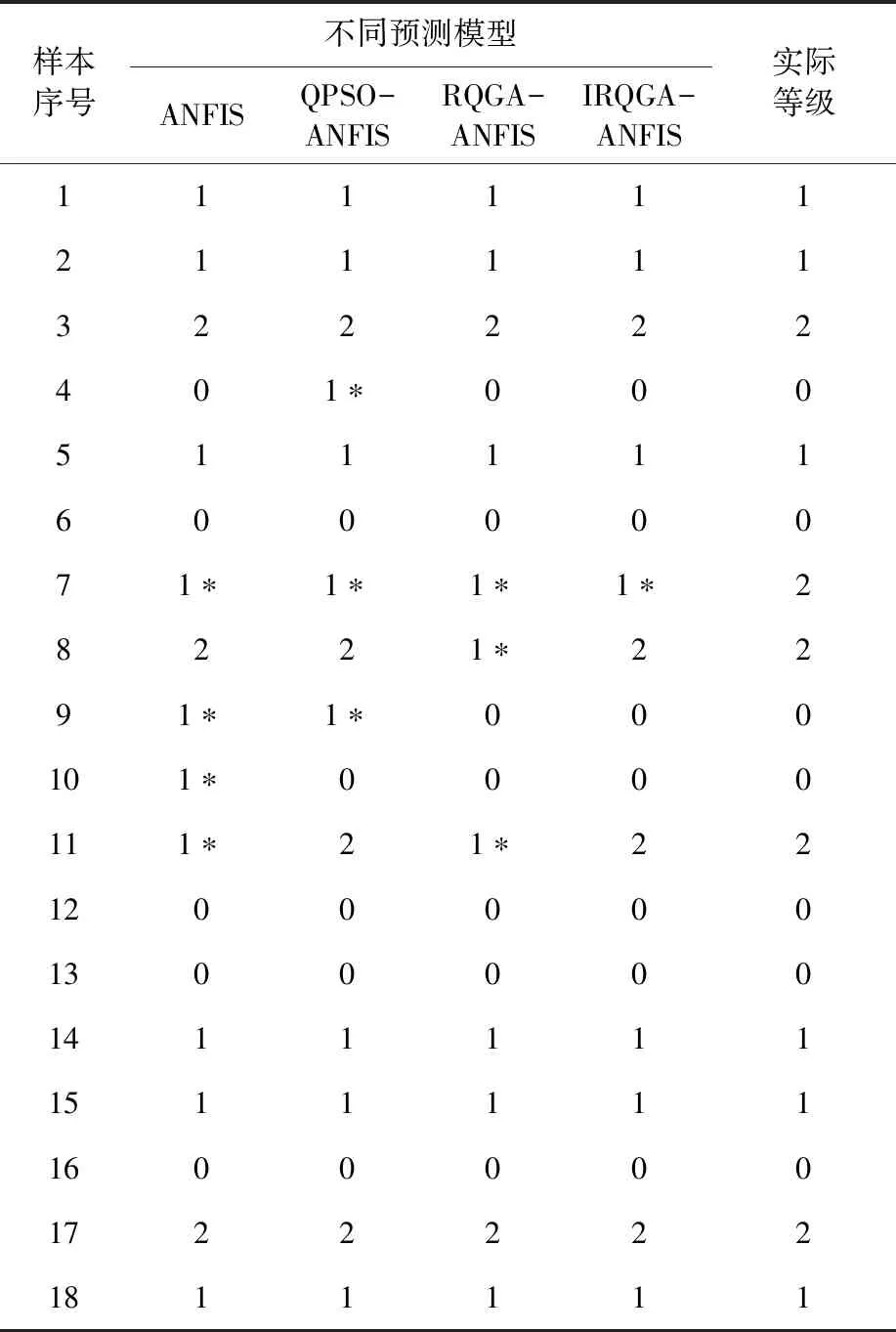
(3)while(t (4) 量子旋转门更新染色体。 (5) 用式(5)~式(12)对量子染色体进行变异更新,对更新后个体进行一次测量并计算个体适应度,若更新后的个体优于原个体,用新个体替换原个体,否则保留原个体。 (6) 用差分变异策略对种群最差个体执行变异操作,对更新后的个体进行一次测量并计算个体适应度,若更新后的个体优于原个体,用更新个体替换原个体,否则以0.5的概率对其部分维度进行均匀初始化变异,变异的维度均为随机选择的若干个维度。 (7) 若全局最优个体连续g代无变化,对种群最优个体实施高斯—柯西变异,若更新后的个体优于原个体,用更新个体替换原个体。 (8)t=t+1 (9) end while 为验证改进实数编码量子遗传算法优化自适应神经模糊推理系统(IRQGA- ANFIS)预测模型的可靠性和准确性,以淮南矿区煤与瓦斯突出事故的部分样本数据为研究对象,进行煤与瓦斯突出危险程度预测。 出于多分类识别和类间样本数量均衡考虑,根据煤岩体抛出的质量将煤与瓦斯突出强度划分为两类,即抛出煤岩体质量小于100t/次为一般突出,大于100t/次为严重突出。据此,将煤与瓦斯突出危险程度划分为三个等级,即无突出、一般突出、严重突出,对应ANFIS的三种输出结果,即‘0’表示无突出,‘1’表示一般突出、‘2’表示严重突出。 数据预处理后获得84组样本数据,数据来源于文献[4]。其中严重突出样本25个,一般突出29个,无突出样本30个,不同类别的样本基本均衡。从中抽取18个样本作为预测样本,预测数据见表1,表中Z1~Z5分别代表瓦斯含量(m3/t)、瓦斯压力(MPa)、孔隙率(%)、煤的坚固性系数和瓦斯放散初速度(mmHg)等输入变量。 表1 煤与瓦斯突出预测数据及危险程度 根据基于数据驱动的模糊规则提取方法,不同覆盖率阈值对应的模糊规则数及ANFIS预测性能对比见表2。从表2可知,ANFIS的模糊规则数为7条时,测试样本的识别准确率为77.78%,测试样本的MSE最小,此时训练样本的MSE和识别准确率相对较好,因此选取7条模糊规则。图1中第一层每个输入变量的论域上的模糊子集个数为7个,待优化的ANFIS网络参数的数量为112个。建模及仿真在MatlabR2016平台实现。 为了对比分析不同训练算法的优化性能,分别用量子粒子群(QPSO)、RQGA和IRQGA优化ANFIS网络参数。算法的最大迭代次数均设为40,种群规模设为20,用拉丁超立方采样方法初始化种群。IRQGA算法的控制螺旋运动轨迹a设为5,移动强度c1和c2均设为2。三种算法分别独立运行30次,30次训练的平均收敛曲线如图2所示。 图2 不同算法的平均收敛曲线 由图2可知,三种算法在迭代初期的收敛都比较迅速,IRQGA后期搜索到的最优个体的平均适应度值明显优于其他两种算法。IRQGA、QPSO和RQGA对ANFIS训练的平均适应度值分别为0.2944、0.3281和0.5018,IRQGA平均迭代12次后就能寻找到RQGA的目标值,说明融合多种进化策略的IRQGA算法有效地提升了基本RQGA的性能。30次独立运行中IRQGA搜索到的适应度值均低于QPSO的0.3281,且平均迭代26次就可搜索到0.3288。由此可知,高维函数优化中,IRQGA具有较强的寻优能力。 分别用ANFIS、QPSO-ANFIS、RQGA-ANFIS、IRQGA-ANFIS对预测样本进行煤与瓦斯突出危险识别,四种预测模型的平均正确预测率分别为77.22%、83.33%、83.33%和94.44%,预测结果见表3。IRQGA-ANFIS对无突出样本的准确预测率达100%。 表3 煤与瓦斯突出预测结果 为评估模型的泛化能力,用30次仿真得到的平均绝对误差(MAE)均值、均方误差(MSE)均值、均方根误差(RMSE)作为评价指标,实验结果见表4。 表4 不同模型预测效果对比 由表4可知,IRQGA-ANFIS在三个评价指标上均有更好的表现。相比QPSO-ANFIS和RQGA-ANFIS,所建模型的MAE均值分别降低了0.0245和0.1184,MSE均值分别降低了0.0162和0.1849,RMSE均值分别降低了0.0172和0.1721。综上可知,IRQGA-ANFIS模型具有较高的预测准确率和预测性能。 (1) 将秃鹰算法的阿基米德螺线空间搜索机制、高斯-柯西变异和差分变异策略引入基本量子遗传算法,提出改进的实数编码量子遗传算法IRQGA,仿真结果表明IRQGA在高维复杂问题优化中比实验对比算法QPSO和RQGA具有更好的优化性能。 (2) 采用基于数据驱动的模糊规则提取方法确定了ANFIS模糊规则数和网络初始参数,降低了ANFIS网络结构设计的复杂度。用改进实数编码量子遗传算法搜索模糊推理系统的最优前提参数和结论参数,提出了煤与瓦斯突出危险程度IRQGA-ANFIS预测模型。实例数据的仿真结果表明,IRQGA-ANFIS模型的MAE均值、MSE均值和RMSE均值都优于QPSO-ANFIS和RQGA-ANFIS模型,IRQGA-ANFIS模型的多分类识别准确率达到94.44%,IRQGA-ANFIS具有更好的非线性映射能力和预测效果,这对煤与瓦斯突出危险预测具有重要的现实意义,同时对其他领域的复杂评价系统也有很好的借鉴意义。3 实例应用

3.1 不同优化算法的性能比较
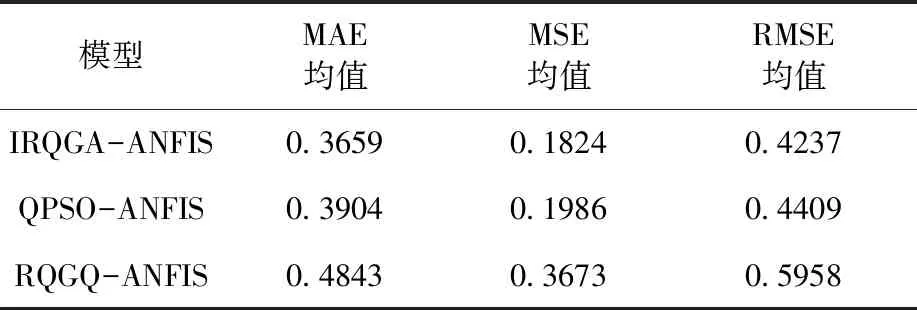
3.2 预测结果分析
4 结论

