基于ALNS算法的机场客舱清洁人员调度研究

林宇鹏，毛 宁，徐国宁，陈庆新，区乐颖

（1.广东工业大学机电工程学院，广州 510006；2.广东机场白云信息科技有限公司，广州 510470）

0 引言

全球货运量和客运量的持续增长给机场服务带来了很大的挑战。不断增长的客机数量也给客舱清洁人员的调度带来了巨大的压力，当前我国机场客舱清洁人员调度仍以人工调度为主，面临的挑战包括任务量大，约束条件复杂。

客舱清洁人员主要为飞机提供清洁服务，进出港航班均需要进行一定标准的客舱清洁服务。不同类型的航班所需的服务不同，大型飞机一般需要3～5组清洁人员，中小型航班一般需要2～3 组清洁人员。为保证清洁服务的质量以及公平性一般要求所有清洁人员到位后才能开始清洁任务[1]。因此，机场客舱清洁人员调度问题本质上是一个具有同步约束的人员路径规划问题（Manpower Routing Problem with Simultaneous Constraints,MRPSC），是经典的带时间窗的车辆路径规划问题的扩展[2]。MRPSC 的任务需要若干人员到同一个地理位置执行一组工作；同时每项任务都有1 个地点，1 个处理时间和1 个时间窗口，人员数量及技能需求。人员可以在不同的时间到达工作地点，但任务需在所有人员都到位后开始，即存在同步约束[3-4]。经典车辆路径规划问题及其扩展中，车辆路径是独立的，不受其他车辆的影响。然而，MRPSC 中的路线通常相互关联，某人员路径的改变可能使得其他人员的路径不合法。MRPSC 是具有多重同步约束的（Vehicle Routing Problem，VRP）的一种类型，其中可能或必须使用一个以上的车辆或资源来完成一项任务[5]。

MRPSC 在很多领域得到了应用。在港口服务领域，Li 等[6]研究了有时间窗和工作团队约束的人力配置问题，采用弧形流公式对该问题进行建模，设计了一种方法来估计所用人员的数量下限，并采用模拟退火算法进行求解。在移动医疗护理领域，通常需要多名工作人员共同服务一名病人，人员调度中同时需要考虑时间窗和人员同步约束[7]。类似地，在机场地面服务中，飞机停靠不同地点，不同职责的地勤人员被安排处理行李、飞机清洁和飞机维修检查等工作[8]。文献[9-11]分别使用自适应大规模领域搜索算法（Adaptive Large-scale Neighborhood Search，ALNS）[12]求解VRP 问题的不同标题，结果表明相对于其他算法，ALNS求解效率与质量更好。

本文以某大型国际枢纽机场为例，综合考虑服务时间窗约束，多需求同时服务等约束，设计出改进的自适应大规模邻域搜索算法求解此复杂而实际的客舱清洁人员调度问题。并通过数值实验和与Gurobi 优化求解器求解结果比较表明，本文设计的ALNS 在求解客舱清洁人员调度问题上，其求解结果稳定且优质。

1 问题描述与数学模型

机场客舱清洁人员调度问题可进行如下描述。给定一个有向图G=(V,A)，其中表示有向图的弧集，tij为经过弧(i,j)∈A的时间；为所有点集，0 点表示清洁人员的休息区，调度开始前所有清洁人员从休息区出发。每个清洁任务i∈N的资源需求为ri。

对于所有清洁任务i,i∈N，其任务服务时长为wi，计划开始服务时间窗为[ei,li]，清洁人员早于ei到达不能立即开始服务，晚于li到达开始计算延误时长，并会产生延误成本。对于清洁人员的休息区，s0= 0。设K为机场所有客舱清洁人员的集合。客舱清洁人员调度问题中涉及的成本分别为任务延误成本和资源转移成本。清洁任务i∈N的延误成本由延误时长与单位延误成本所得，对清洁人员k∈K的转移成本由转移时长与单位转移成本所得。

在上述问题描述的基础上，引入以下变量并构建问题的数学模型。

xijk：若xijk= 1，则表示清洁人员k执行从任务i到任务j的服务路线，否则xijk= 0。

si：清洁任务i的开始服务时间。

di：清洁任务i的延误时长。

目标（1）是最小化客舱清洁任务延误成本和清洁人员转移成本，α和β分别是延误时间和转移时间的成本系数。式（2）表示保证所有客舱清洁任务满足标准人力需求。式（3）表示清洁人员k 服务前后两清洁任务必须满足服务时间和转移时间约束，其中M为极大值。式（4）～（5）表示所有客舱清洁人员从休息区出发，并最终返回到休息区。式（6）是客舱清洁人员的流平衡约束，表示清洁人员服务完成任务i后必须从任务i出发前往下一个任务进行服务。式（7）表示客舱清洁任务的延误时长，如果si≥li，di=si-li，否则di= 0。式（8） ～（10）表示各变量的取值范围。

2 求解算法

2.1 算法架构

本文中的VRPMS 问题是VRP 问题的拓展，因此也是一个NP-hard 问题。通过使用商业求解器对该问题的数学模型进行求解可知，精确算法只能求解小规模数据，但实际应用中的调度规模往往比较大，为了应对实际中客舱清洁人员调度问题，本文设计了改进的ALNS算法。

ALNS 算法的基本流程如图1 所示。首先通过贪心算法构建问题的初始解s，并设置为当前解；然后在后续每一次迭代过程中，将q个任务随机选择一种移除算法从当前解中移除，接着将这q个任务随机选择一种修复算法修复到当前解中，进而得到一个新解s′；将退火机制引入到新解s′的判断中；最终迭代到指定次数后终止。

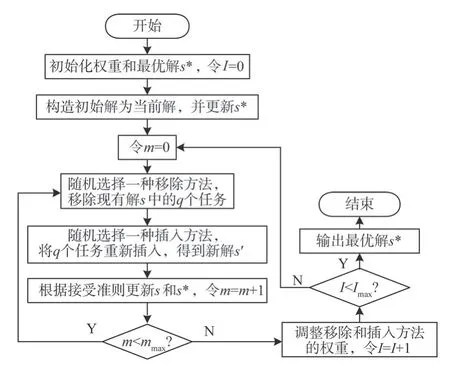
图1 ALNS算法流程

本文ALNS 算法的移除和修复算法权重的更新主要使用轮盘赌的方式进行选择，假设wi为第i中方法的权重，开始迭代时所有算法的初始权重为w0。修复算法和移除算法权重的更新方式相同，但两者的选择相互独立。迭代过程中，修复与移除算法权重的更新主要根据新解s′的表现进行打分。打分情况分为新的最优解、比当前解好、比当前解差但被接受了，得分为σ1,σ2,σ3。本文各方法的权重更新以50 次迭代为一周期，一个周期结束后对各种移除和修复算法进行评分调整。设wij表示算法i在第j段中的权重；πij表示算法i在第j段中的总得分、θij表示算法i在第j段中被选用的次数，则算法i在第j+ 1段的权重更新如式（11）所示。

式中：λ为影响因子，表明权重受新评分影响的程度。

2.2 初始解与时间更新机制

2.2.1 构建初始解

本文初始解的建立基于贪婪算法，客舱清洁人员调度模型中带有软时间窗约束，因此生成初始解时优先考虑插入位置的延误成本。初始解的主要构建步骤如下。

（1）定义D为未安排资源的清洁任务，令D=N。（2）当 ||D＞0 时，①随机选择一个任务i∈D，②计算任务i插入到各资源路径中的插入成本P(s)，③将任务i插入P(s)最小值对应的位置，令D=D-{}i，返回步骤2。

（3）输出初始解。

2.2.2 时间更新机制

由于多需求同时服务任务同时需要多个清洁人员继续服务，这使得清洁人员的路径通常是相互关联的。当此类任务的开始服务时间发生调整，将会影响该任务所涉及的资源路径，这些资源路径后续任务的开始服务时间理应跟着发生调整，这种影响存在传递性。ALNS 算法在对当前解进行插入或者移除过程中，需要对插入或移除任务后当前解中各任务节点的服务时间进行更新，并且需要更新当前路径的成本。

为了实现快速调整任务发生变化后各节点时间的变化，将一种“时间更新机制”引入到算法中。当有任务插入到现有解后，首先找到该任务的所有后续任务，假设为集合H，对集合H中的任务根据开始服务时间升序排列；然后，按照集合H的中任务顺序依次更新任务的开始服务时间。以图2 展示的插入例子为例，图2 （a）中3 各清洁人员的服务路径，其中线条表示路径，圆表示任务，方框表示清洁人员休息区，现有路径为A1:1 →3 →6,A2:2 →3 →5,A3:2 →4 →5。假设任务7插入到A2 路径中，如图2 （b）所示。首先获取任务7的所有后续任务集合H={3,5,6}，对集合H进行升序排列，按照任务开始服务时间顺序逐个进行服务时间更新。首先调整任务3，如图2 （c）所示，最后调整任务5 和6，如图2 （d）所示。

图2 服务时间调整例子

2.3 移除算法

本节分别介绍随机移除法、最坏路径移除法、Shaw移除法和最坏值移除法。它们的共同目的是从当前解中移除q个任务，并在移除后通过时间更新机制更新路径中每一个任务的服务时间。其中，引入参数p增加Shaw移除法和最坏值移除算法的随机性，以便扩大搜索范围、避免陷入局部最优。

2.3.1 随机移除法

随机移除法从当前解中随机选择q个任务，然后将这q个任务从解中移除。由于随机性较高，修复后质量不稳定，但是运算速度快。

2.3.2 最坏路径移除法

最坏路径移除法是从已有路径中选择成本最高的路径，移除该路径上所有任务。若移除的任务数少于q位，则再选择成本次高的路径进行移除。重复此过程知道移除总数不小于q位。

2.3.3 Shaw移除法

Shaw 移除法是由Shaw[13]在1997年提出，通过任务之间的共同属性计算不同任务的相似度，从当前路径中移除相似度较高的任务。实验表明，移除相似的任务可以帮助后续路径修复得到更优的解，而移除相似度较低的任务会得到较差或原来的结果。

本文任务间相似度的定义是通过任务的最早开始服务时间、服务时长以及相对距离同时引入φ、ω和τ作为三者的权重计算而得。具体的计算公式如式（11）所示。

图3 为Shaw 移除法的算法流程。首先在路径任务集合L中随机选择一个任务r，并将r放入移除任务集合D中；接着，在移除任务集合D中随机一个任务i，计算当前路径任务集合L中所有任务与任务i的相似度R(i,j)，然后根据公式选择一个相似度较高的任务移除路径，其中y是服从[0,1）均匀分布的随机数，p是增加算法随机性的参数。

2.3.4 最坏值移除法

最坏值移除法是将当前解中移除成本较高的任务移出当前路径。图4 为该方法的算法流程。计算所有任务从当前解移出后的成本减少量ci，然后根据选择一个移出成本较高的任务进行移出，其中y是服从[0,1）均匀分布的随机数，p是增加算法随机性的参数。

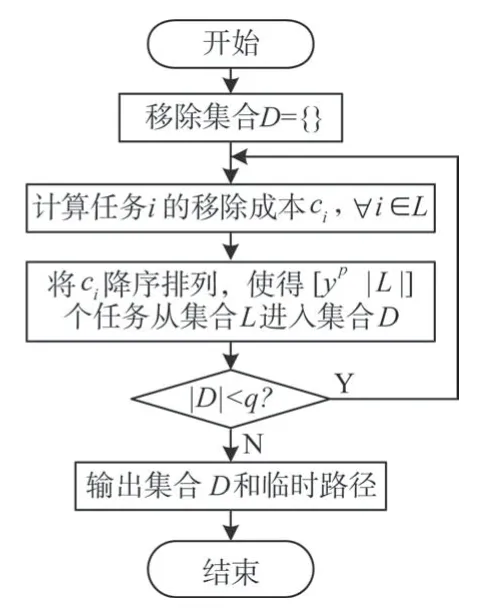
图4 最坏移除法的流程

2.4 修复算法

本节介绍的修复算法主要由贪婪修复法和后悔值修复法，按一定优先规则将已移除的任务重新插入到当前路径中并产生新解，每次插入过程中需要对任务进行时间调整。

2.4.1 贪婪修复法

贪婪修复法的具体步骤如图5 所示。首先计算在移出集合D中所有任务插入现有路径后总成本的增加量，Δg(i)为所有增量中的最小值，h(i)代表Δg(i)对应的最优位置。选择集合D所有任务中Δg(i)最小的值相应的任务r，将任务r的插入到h(r)对应的位置上。重复上述过程，直到所有任务都被重新插入为止。

图5 贪婪修复法的流程

2.4.2 后悔值修复法

后悔值修复法的具体步骤如图6 所示。该算法参考贪婪修复法计算每一位在移除集合D中的任务i插入到现有服务路径各位置后路径总成本的增加量。然后将各增量升序,第i位的值为Δgj(i)，h(i)代表Δg1(i)对应的最优位置。任务i插入到最优位置的后悔值计算公式为：

图6 后悔值修复法的流程

选择集合D所有任务中Δr(i)最小的值相应的任务r，将任务r的需求插入到h(r)对应的位置上。重复以上的步骤，直到所有移除集合D中的所有任务都重新插入到路径中。

2.5 接受新解和算法终止

产生新解s′后，还需对s′进行判断能否被接受。为了避免算法陷入局部最优，本文算法引入了退火机制。对于比当前解s差的新解s′，以一定的概率f接受s′。f的计算方法如式（14）所示。本算法采用最大迭代数作为算法的终止准则。

3 算法实验

本文的实验数据选取某大型机场的航班信息，对应的客舱清洁任务整理生成多种规模算例进行求解实验。并通过与Gurobi9.5 求解器的求解结果进行对比，验证了混合整数规划模型的正确性和ALNS 算的有效性与高效性。程序都在Windom 环境下，硬件环境包括AMD（R） Core （TM） 3700X CPU @ 3.60 GHz，16.00 GB 内存。Gurobi限定求解时间为3 600 s，ALNS限制最大迭代次数为3 000次。

3.1 算例说明和参数设置

算例数据来源于机场实际的客舱清洁人员调度背景，为了验证算法在不同规模下的有效性与高效性，分别设计小、中、大3 种规模。小规模的清洁人员数量Knum∈{15,20}，清洁任务数量Nnum∈{15,20,25} ；中规模清洁人员数量Knum∈{35,40} ， 清洁人员数量Nnum∈{40,45,50} ；大规模清洁人员数量Knum∈{45,50}，清洁人员数量Nnum∈{}80,100,120 。利用18 个算例对σ1,σ2,σ3,p,λ做参数测试，结合参考文献[14-16]，最终算法的参数设置如表1所示。

表1 参数设定

3.2 实验结果对比分析

本节将Gurobi求解结果与本文ALNS算法的求解结果进行对比分析。比较结果如表2 所示，其中“UB”和“LB”分别表示Gurobi结果的可行解和下界；“Time”为两者方法的求解时间；“Gap”通过可行解和下界计算得来；“Best”表示10次求解结果中的最优值，Avg表示10次求解结果的平均值，Time表示10次求解平均耗时；表中“精度”列表示ALNS相对于Gurobi的结果提升了程度；“—”表示Gurobi 未能在规定时间内找到可行解，“*”表示Gurobi找到最优解，加粗的结果表示两者中结果较好的一个。

表2 ALNS算法与Gurobi求解结果比较

由表2 可知，本文设计的所有18 个算例中，ALNS算法的求解结果大部分都优于或等于Gurobi的求解结果。对于小规模算例，Gurobi都能在1 s内找到最优解，同样的ALNS 也能在较短的时间内找到最优解，同时10 次求解平均结果与最优解也十分接近。对于中规模的6 个算例和大规模的6 个算例，Gurobi 均无法在3 600 s 内求得任一精确解，同时大规模算例中有3 个算例Gurobi 无法在规定时间内找到可行解。在中大规模的12 个算例中，Gurobi 仅有4 个算例的结果优于ALNS，同时ALNS 的算法的平均结果与Gurobi 可行解的精度相差在8%以内，其余8 个算例ALNS 的求解结果均优于Gurobi 求解结果。在运行效率上，Gurobi 对于中大规模的算例相对比较耗时，求解效率不高，ALNS 算法的求解时间虽然也会因规模的变大而增大，但总体求解时间相对较低。

综上所述，无论是有效性还是求解效率上，ALNS算法的结果更优。

4 结束语

本文描述了带任务服务时间窗和多需求同时服务的客舱清洁人员的调度问题，建立其混合整数规划数学模型，为求解该问题设计了一种结合贪婪算法生成初始解的自适应大规模领域搜索算法。结果表明，ALNS 算法能够得到该问题稳定且优质的调度方案，对实际的清洁人员调度有很强的指导意义。从与Gurobi 对比的实验结果可以看出，该算法的设计合理且高效，其求解结果无论是在效率和质量上均优于大型商业求解器，对日常的客舱清洁人员调度问题提供了新的解决方案。当前的研究主要集中在任务到达、任务服务时长静态的条件下，而在不确定性方面，可以继续开展在任务到达与作业时长随机条件下的客舱清洁人员调度方面的研究。