融合二维压缩感知和同步混沌流密码的医学图像加密算法*
叶柏君,林卓胜,吴小娜,邓景良,曾慧曲
(五邑大学智能制造学部,广东 江门 529020)
0 引言
如今,随着信息技术和成像技术的发展,医学影像普遍应用于病理学的诊断中,这其中包含有X 射线、磁共振成像、CT 成像、超声成像等。而在医学影像中包含着大量患者的隐私信息,因此对医学影像进行保护使其免受各种网络攻击,避免信息丢失和保证完整性尤显重要,其中最有效的办法就是对其实施加密。
混沌系统具有长期不可预测以及对初始条件高度敏感等特性,常应用于图像加密领域。Zhang 等[1]提出了一维压缩感知和混沌系统的医学图像加密算法,采用Chebyshev 混沌映射生成测量矩阵及Logistic 映射生成密钥流。为提高医学影像加密的鲁棒性,学者们主要从新混沌系统的构建以及加密方案的设计等方面开展研究。如Liu 等[2]所提出的双曲正弦混沌系统。Belazi 等[3]采用SHA-256 哈希函数与初始密钥一起用于产生混沌系统的密钥且结合DNA 编码。Yang 等[4]提出采用分数阶超混沌系统与DNA 编码相结合的图像加密方案。Mortajez等[5]则从明文图像中提取密钥,基于Logistic 混沌系统对图像像素进行排序并进行异或运算加密。Javan 等[6]研究两个超混沌系统的多从同步和一主系统同步以及循环同步的加密方式。Salman 等[7]对图像中包含敏感信息的区域采用二次映射进行选择性加密。
压缩感知在压缩图像时在一定程度上能够降低像素之间的相关性,因此许多研究者提出了将压缩感知和其他图像加密方式相结合的压缩-加密方式。与一维压缩感知相比,二维压缩感知是生成两个测量矩阵分别对图像的行和列分别进行测量压缩,大幅度提升了的压缩性能。Wang 等[8]提出一种由Tent-sine 映射生成测量矩阵,并通过Logistic-Sine映射、Logistic-Tent映射生成密钥流,结合拉丁方阵实现测量矩阵的加密。Deng等[9]使用Logistic映射生成测量矩阵,并通过离散分数随机变换对图像进行加密。Xu等[10]提出了一种基于2D-SLIM 和压缩感知的快速图像加密算法,有效降低了时间复杂度。Liu等[11]提出一种二维压缩感知和双随机相位编码的图像加密算法,由于双随机相位编码具有的光学实现和鲁棒性高等优点,保证了图像加密的安全性。Gan等[12]利用明文图像的信息熵和外部密钥生成混沌系统的初始值,并通过2D-LSCM和4D-忆阻混沌系统分别生成测量矩阵和伪随机序列,实现对明文图像的压缩感知和加密,可以抵御已知明文和选择明文攻击。在Chai等[13-14]及Hou[15]提出将二维压缩感知和嵌入技术相结合的视觉安全加密算法中,使用了均匀量化及Sigmoid量化以保证算法的加密性能及解密精度。
本文设计一种基于二维压缩感知和同步混沌流密码系统的图像压缩-加密算法。首先,迭代同步混沌流密码系统得到用于二维压缩感知的测量矩阵和用于加密的伪随机序列,然后分别从行和列两个方向对医学图像进行测量,再对测量后的图像进行量化及加密。而Tanh 函数与Sigmoid函数都为机器学习中常用的激活函数,均可将输入数据值映射到一定区间范围内,为此,本文对采用均匀量化、Tanh 函数量化和Sigmoid 函数量化三种量化方式对算法的性能影响进行比较。
1 基础知识
1.1 压缩感知
一维压缩感知的压缩采样过程可以描述为:
式中:Φ为观测矩阵;Ψ为稀疏基矩阵;Ω为稀疏系数;Θ为ΦΨ的乘积,为传感矩阵。
为了能够实现信号x的恢复,传感矩阵需要满足约束等距性条件(RIP):
式中:δk为等距常数。
稀疏信号可以通过如下最小化进行重建:
在二维压缩感知(2DCS)中,从两个方向上使用两个测量矩阵对信号进行采样。设图像X1的大小为N×N,则对X1的稀疏表示为:
式中:Ψ的大小为N×N。
对于2DCS的采样过程如下:
Φ1、Φ2分别对X1的行、列方向进行测量。为了实现从Y到X1的重建,需要解决以下的优化问题。
1.2 同步混沌流密码系统
混沌系统拥有对于初始状态的高度敏感性,基于其复杂的动力学行为,使得所生成的混沌序列难以分析与预测。本文所使用的六维离散混沌系统的动力学方程如式所示。
式中当参数设置为:a11=0.38,a12=-0.12,a13=0.28,a14=-0.12,a15=0.08,a16=-0.32,a21=-0.04,a22=0.06,a23=0.36,a24=-0.04,a25=0.16,a26=-0.24,a31=0.12,a32=-0.28,a33=0.42,a34=0.12,a35=0.12,a36=-0.28,a41=0.20,a42=-0.20,a43=0.20,a44=0.10,a45=0.20,a46=-0.20,a51=0.08,a52=-0.32,a53=0.28,a54=-0.12,a55=0.38,a56=-0.12,a61=0.16,a62=-0.24,a63=0.36,a64=-0.04,a65=-0.04,a66=0.06,ε1=1′107,ε2=2′107,ε3=3′107,σ1=4 000,σ2=5 000,σ3=6 000 时,其混沌吸引子如图1所示,计算出的李雅普诺夫指数分别为λ1=11.427 9,λ2=11.373 5,λ3=10.658 3,λ4=10.658 3,λ5=3.895 4,λ6=3.886,表明系统处于超混沌状态。

图1 混沌吸引子相图
由混沌序列生成伪随机序列S的方式为:
式中:xi为混沌系统迭代生成的混沌序列。
加密运算的表达式为:
式中:p(k)为密文;m(k)为明文;S(e)为加密端用的伪随机序列。
解密运算的表达式为:
当解密运算和加密运算所用的伪随机序列相等时,即S(d)(k) =S(e)(k)时,=m(k)。
1.3 Tanh函数
Tanh 函数为双曲正切函数,由于其具有的双侧饱和性和0 均值特性,常作为机器学习的激活函数,Tanh 函数的映射空间为[-1,1],可以通过调整函数的振幅和斜率得到所需的输出区间值,其定义式如下:
式中:α、β为常数。
Tanh函数的逆函数为:
2 本文算法
2.1 算法框图
本文所提出的基于二维压缩感知和同步混沌流密码系统的加密及解密算法框图分别如图2~3所示。

图2 加密算法

图3 解密算法
2.2 图像加密
本文所提出的加密方案主要分为明文图像的小波变换、伪随机序列的生成、压缩感知测量、量化以及加密5个部分,具体步骤如下:
1)输入尺寸大小为M×N的医学图像I,确定明文图像所需要的压缩比CR;
2)对明文图像I进行二维离散小波变换得到同样大小的稀疏图像I1;
3)将6个初始值与42个参数代入加密端六维同步混沌流密码系统,根据式(6)迭代生成混沌序列。序列的长度设置为M×N×CR+ 256,并舍弃前256 个序列,得长度为M×N×CR的混沌序列x4、x5、x6;
4)将混沌序列x4、x5缩小109,按列重新排序得到大小分别为(M×CR)×N、M×(N×CR)的测量矩阵Φ1、Φ2;
5)利用所生成的测量矩阵根据式进行测量,得到测量后尺寸大小为(M×CR)×(N×CR)的图像I2;
6)利用式(8)对图像I2进行量化得到量化后的图像I3;
7) 取伪随机序列x6的前×M×N个值代入式(11)得到加密端伪随机序列S(e),对图像I3按式进行加密运算,最终得到密文图像C。
2.3 图像解密
解密算法为加密算法的逆过程,接收端到密文图像C,需要进行解密操作和恢复重建,其步骤简述如下:
1) 将6 个初始值与42 个参数代入解密端六维同步混沌流密码系统迭代生成长度为M×N×CR+ 256 的混沌序列,并舍弃前256 个序列,得到长度为M×N×CR的混沌序列x4、x5、x6;
2) 取混沌序列x6的前×M×N个值进行量化,得解密端伪随机序列S(d),根据式(10)对密文图像C进行解密运算,得到解密图像P1;
3)对图像P1进行逆量化,得逆量化后的图像P2;
4)利用ONSL0 恢复重建算法对图像P3进行重构,得到恢复的重建图像P3;
5)对图像P3进行离散小波逆变换,得到解密端的最终图像P4。
3 实验结果及对比
3.1 实验结果
当输入医学图像的尺寸大小为512 × 512,压缩比设置为0.5× 0.5,Tanh 量化函数的参数设置为α= 510、β= 0.012 5时,根据所提算法分别对CT、MRI、B超及X光等4种不同类型的医学图像进行加解密,结果如图4所示。可以看出,压缩加密后的图像尺寸大小仅为原图像的1 4,有效减少了图像的尺寸。且加密图像均为类雪花状,无法从中看出原医学图像的内容。恢复重建后的图像与原图像基本一致,说明了所提算法的有效性。
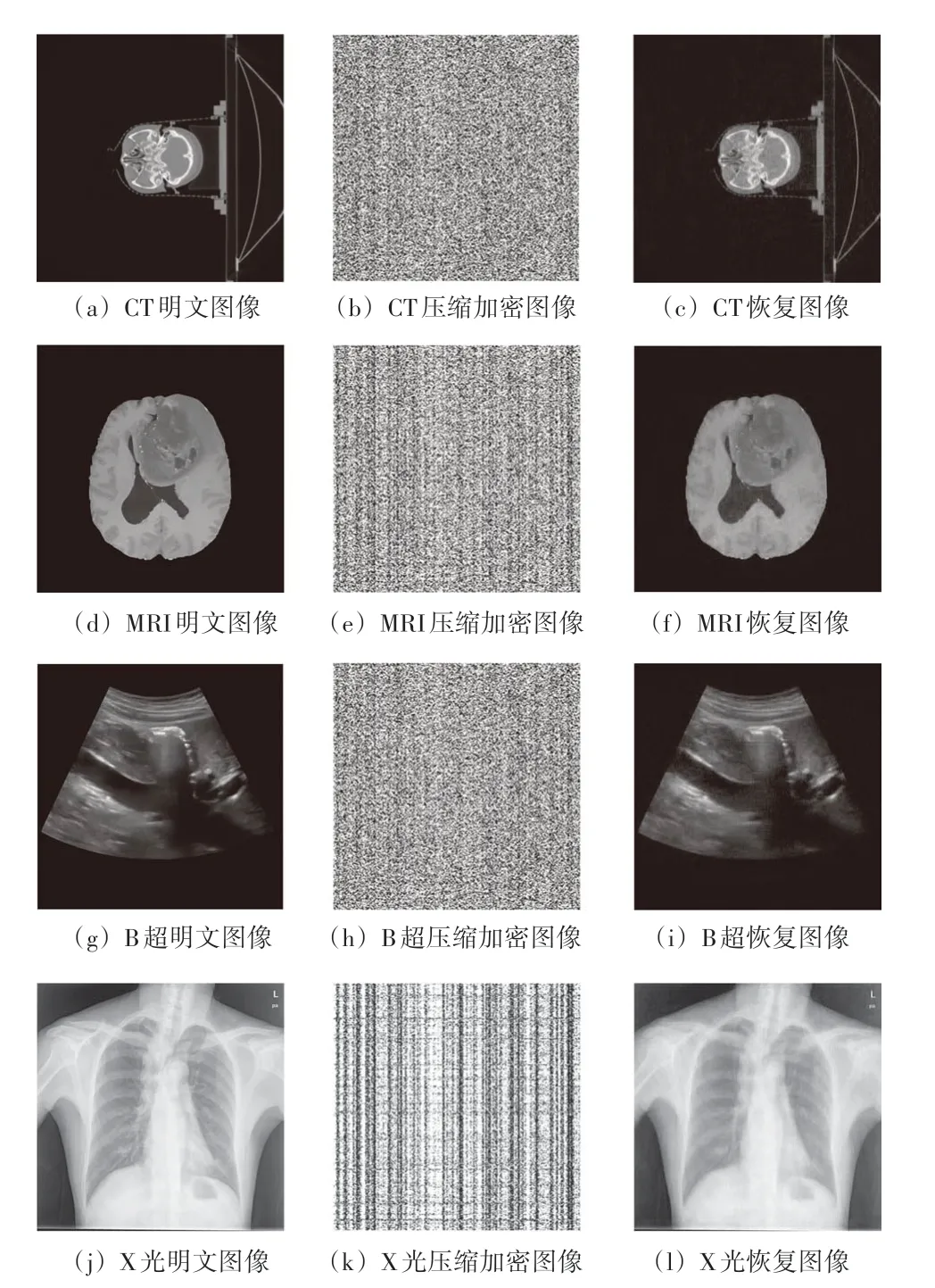
图4 实验结果
3.2 量化性能对比
为测试不同量化函数对本文所提算法的影响,分别使用均匀量化函数、Tanh 量化函数及Sigmoid 量化函数在不同压缩比下针对不同图片进行压缩加密和恢复重建,结果如图5 所示。图中的(a)、(b)、(c)分别对应实用均匀量化函数、Tanh 量化函数及Sigmoid 量化函数时重构图片的峰值信噪比(PSNR)变化曲线。

图5 不同量化方式不同压缩比下的PSNR值变化图
在图5(a)中由于均匀量化中的取整的误差会导致其PSNR 值在0.6 × 0.6 压缩比之后其值会进行回落;在图5(b)中,对于不同类型的医学图像,采用Tanh 量化函数时,随着压缩比的增大,PSNR 值稳步上升;而在图5(c)中X 光图像在压缩比为0.5 × 0.5 和0.7 ×0.7 时,PSNR 值会产生较大的波动,这是因为采用Sigmoid 量化后的图像,其左上角的一部分区域会计算得到复数。从对比结果可以看出,相较于均匀量化及Sigmoid 函数量化,采用Tanh 函数进行量化具有更稳定的PSNR 值。
3.3 密钥空间
假设计算机的计算精度为10-14,密钥为6 个初始值及 42 个 参 数 , 本 文 总 的 密 钥 空 间 为(1014)48= 10672≈22818,远远大于2100,因此本方案的密钥空间足以抵御穷举攻击。
3.4 直方图分析
图6的结果中可以看出4种医学明文图像的直方图是不均匀的;加密后,CT、MRI、B 超和X 光图像的密文图像是比较均匀的,而X 光这表明经所提算法加密后的医学图像具有良好的统计特性。
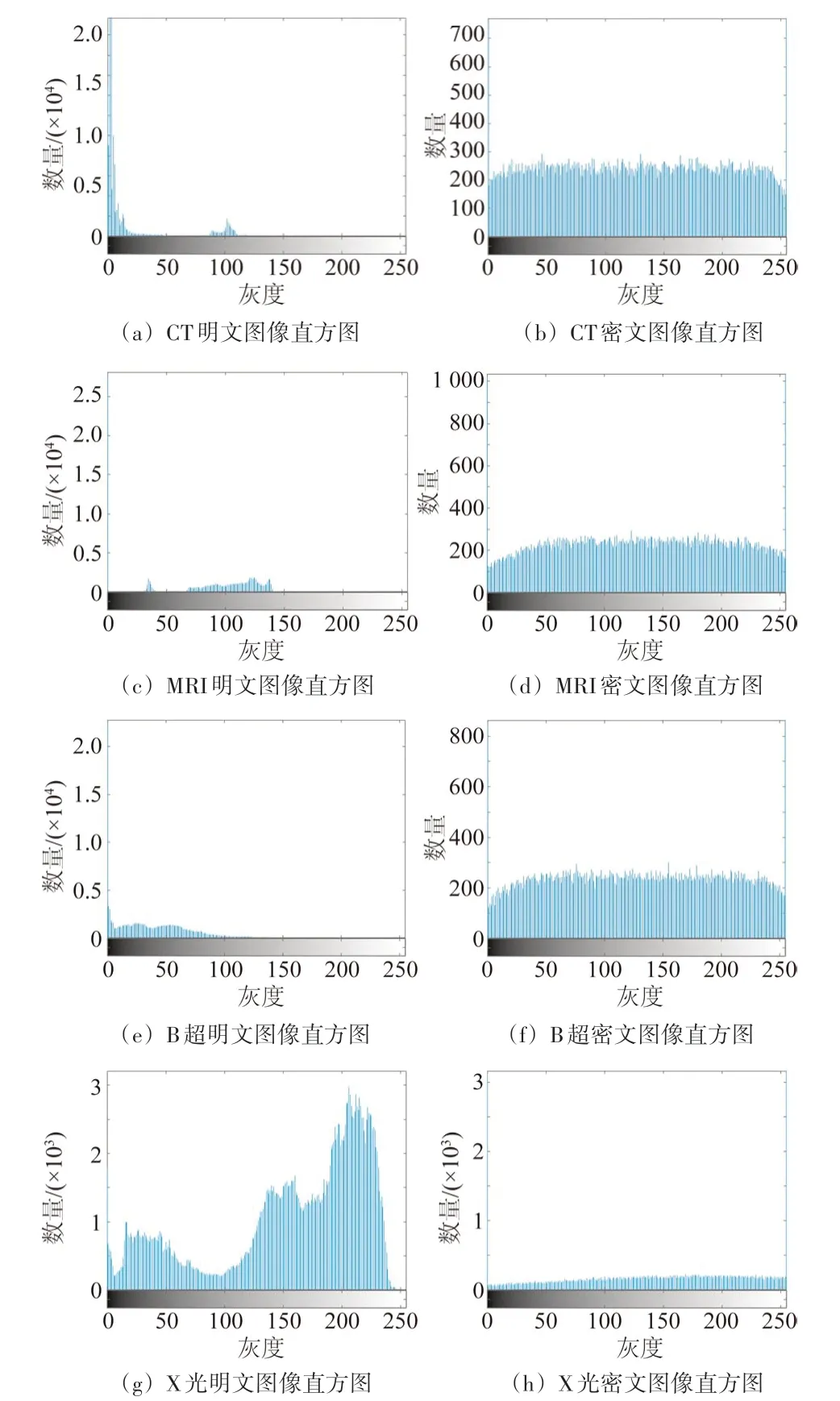
图6 明文图像、密文图像直方图
3.5 相关性分析
在明文图像和对应的密文图像中,我们随机选取10 000 对相邻像素,分别计算了其在水平、垂直、对角方向的相关性。本文算法对于不同图像,不同方向的相邻像素之间的相关性系数计算结果如表1 所示,结果表明本文所提算法可以有效地降低CT、MRI、、B 超和X 光图像的相关性系数。

表1 明文图像和密文图像的相邻像素间的相关系数
如表2 给出的CT 图像同其他论文的比较结果中,本文所提算法在相邻像素间的相关性上略高于其他文献,这主要是因为二维压缩感知使得加密后的图像尺寸变小而导致的。

表2 CT图像的相关性系数与其他文献比较
3.6 剪切攻击
抗剪切分析以CT 图像为测试图像,压缩比为0.5×0.5,量化函数的参数均为α= 510、β= 0.0125。
由图7~8 及表3 可知,当剪切量为5%时,图像还可以分辨,但剪切量为15%时,图像基本不能分辨,但是依然还是可以恢复部分信息,因此,本文加密算法在一定程度上可以有效抵御剪切攻击。

图7 不同剪切度下的密文图像和恢复图像

图8 不同剪切度下的密文图像和恢复图像
3.7 噪声攻击
抗噪声分析以CT 图像为测试图像,压缩比为0.5×0.5,量化函数的参数均为α= 510、β= 0.0125,分别添加不同标准差的高斯噪声和不同密度的椒盐噪声,结果如图9及表4所示。

表4 不同噪声强度下CT图像的明文图像与密文图像PSNR值

图9 不同噪声强度下CT图像的恢复图像
由结果可知,随着所添加高斯噪声和椒盐噪声的增加,恢复重建图像的PSNR 值也会随之下降,但从视觉上仍可分辨出图像的特征。与添加椒盐噪声相比,添加高斯噪声对恢复重建图像所带来的影响较小。因此,本文所提算法具有一定的抗噪声能力。
3.8 选择明文攻击
攻击者一般选择全黑图像或全白图像对图像加密算法实施攻击。根据本文所提算法,全黑图像及全白图像的相邻像素间的相关性系数(见表5)及实验结果图(见图10)可以发现,全黑图像加密后仍呈现类雪花状,而全白图像的加密效果则与X光图像的加密效果类似,即攻击者也无法直接根据密文图像获取明文图像的全部特征。因此,本文所提算法具有一定的在抵抗选择明文攻击能力。

表5 全黑和全白图像的相关性分析

图10 全黑及全白图像的明文图像、密文图形及密文直方图
4 结束语
本文提出一种基于二维压缩感知和同步混沌流密码系统的医学图像加密算法。从实验结果可以看出,所提算法对CT、MRI、B 超以及X 光图像可以表现出良好的保密效果。四种医学图像在不同压缩比下的量化对比结果表明,相较于均匀量化函数及Sigmoid量化函数所提算法采用Tanh 函数进行量化能使得恢复重建出的图像具有更稳定的PSNR 值。通过直方图分布和相邻像素相关性等统计分析,结果表明所提算法在一定程度上可以抵抗统计攻击;并且在抵抗裁剪攻击、噪声攻击和选择明文攻击等相关实验结果中,所提算法表现出较好的鲁棒性和安全性。因此,本文所提出算法在医学图像加密方面具有一定的实际应用价值。

