基于扩展卡尔曼滤波的动力电池SOC估算

潘正军，袁兴有，邓飞虎，岳 姗，徐 霞

基于扩展卡尔曼滤波的动力电池SOC估算

潘正军1，袁兴有1，邓飞虎1，岳 姗1，徐 霞2

（1.金肯职业技术学院，江苏 南京 211156；2.常州交通技师学院，江苏 常州 213147）

卡尔曼滤波（KF）是基于最小方差估计的一种最优估计方法，适用于线性系统，而车载动力电池在实际运行过程中具有较强的非线性特征。通过对卡尔曼滤波进行改进得到扩展卡尔曼滤波（EKF），可以较好地解决这一问题。文章以三元锂电池为研究对象，建立一阶RC等效电路模型作为电池的基础模型，在锂电池充放电的试验数据基础上，利用MATLAB进行拟合得到电压与电池荷电状态（SOC）的关系曲线OVC-SOC，利用最小二乘法进行参数辨识，再利用EKF算法对动力电池SOC进行实时估算。

动力电池；一阶RC；EKF；SOC估算

能源是支撑社会发展的重要基础，电动汽车由电池提供动力来源，具有零排放、节能环保与无污染等优点，传统燃油车逐渐被其取代。作为电动汽车的直接驱动能量来源的动力电池，其整体性能会影响到电动汽车的行驶里程，制动能量回收效率和动力特性等，进而影响到整车的可靠性及成本[1]。

为了保证电动汽车安全可靠地运行，需要一套优良的电池管理系统（Battery Management System, BMS）对电池进行状态监测、能量均衡和热管理。电池的状态检测参数主要包括电流、电压、温度、电池荷电状态（State Of Charge, SOC）和健康状态。其中电池荷电状态SOC是BMS所监测的重要状态量之一，它反映了电池的剩余容量，是整个汽车充电和放电控制策略以及电池均衡工作的基础[2]。准确实时的电池SOC估计可保证BMS进行电池能量均衡管理，避免电池过充过放，延长电池使用寿命，并为驾驶者及时提供续驶里程等信息，便于合理规划其行程[3]。

目前常用的电池SOC估算方法有放电实测法、开路电压法、电流积分法、神经网络法、负载电压法、模糊逻辑法、卡尔曼滤波法等[4]，其中卡尔曼滤波法与神经网络分析法可以达到较高的估算精度，其他方法因估算误差较大、噪声降低效果不理想等缺点，难以实现SOC的精确估算。在研究SOC估算中，经常以电流、电压和电阻等因素作为修正因子，提高参数的准确性，从而实现电池SOC的精确估算。

本文在卡尔曼滤波的基础上，针对非线性状态估计问题，采用扩展卡尔曼滤波（Estimation Kalman Filter, EKF）算法进行估算电池SOC，构建一阶RC电池等效电路模型，根据锂电池充放电的试验数据，对电池进行参数辨识，利用MATLAB/ Simulink实现EKF算法进行仿真验证。

1 锂电池一阶等效模型建立

对于基于EKF算法的动力电池SOC估算，准确建立等效模型对估算精度将产生直接影响。目前常用的动力电池系统模型包括电池机理模型、等效电路模型和神经网络模型[5]。对于电池机理模型，由于其含有非常复杂的偏微分方程和繁多的电化学参数，对BMS的运算能力造成了极高的挑战。而神经元网络模型需要大量的试验数据来预测电池的性能，对于数据依赖比较大。

目前最常见的等效电路模型一般有Rint模型、Thevenin模型、PNGV模型和GNL模型。Rint模型结构简单、参数容易确定，一般仅用于对精度要求不高的场合。Thevenin相比于Rint模型，增加了并联的RC环，用于模拟电池内部的极化特性，从而克服了Rint模型在动态特性方面的缺陷，而且该模型还考虑了开路电压和电池SOC的动态过程，能够准确地模拟电池的充放电过程。PGNV与Thevenin电池模型相比，增加了一个电容来描述锂离子在正负极上的逐渐积累，因此模型参数辨识比较复杂。GNL是对上述三种模型的结合与发展，可以更好地模拟电压的变化过程，但结构最为复杂，不适用于工程应用。综合考虑电池模型精度和算法复杂度，建立如图1所示的含有一阶RC的Thevenin电池模型。

图1中，oc为电池开路电压；0为电池内阻；1为电池极化内阻；1为电池极化电容；t代表电池的端电压。根据基尔霍夫电压电流定律可得

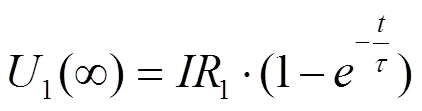
基于安时积分法的SOC计算公式如下：

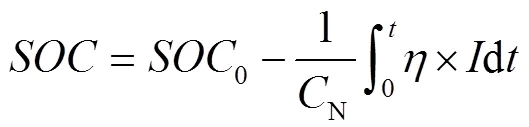
式中，SOC为当前电池电量；SOC0为电池的电量初始数值；为回路中的电流；N为电池额定容量；为库伦效率；为时间。

2 基于EKF算法的SOC估计

2.1 卡尔曼滤波原理

卡尔曼滤波（Kalman Filtering, KF）是一种使用线性系统状态方程通过系统输入和输出观测数据优化和估计系统状态的算法。由于观测数据中含有噪声和干扰的影响，因此，最优估计可以被视为一种滤波过程[6]。数据滤波是一种数据处理技术，用于消除噪音和恢复原始真实数据。当已知测量方差时，Kalman滤波可以通过对带有测量噪声的一系列数据进行处理，估计动态系统的状态。Kalman滤波是目前应用最广泛的滤波方法，它便于计算机编程，能实时更新和处理现场采集的数据，在通信、导航、制导和控制等领域得到了广泛的应用[7]。

对于动态系统，用状态空间模型描述如下：

式中，为离散时间；()为时刻系统输入；()、()分别为系统噪声和观测噪声；为系统矩阵；为输入矩阵；为输出矩阵。

由于电池系统的非线性，直接利用卡尔曼滤波算法进行模型参数辨识或状态估计会产生比较大的误差。扩展卡尔曼滤波的核心是线性化，利用一阶泰勒公式展开方法，对非线性系统方程进行处理，使原系统成为线性系统，然后再运用标准Kalman滤波算法的思想对系统的线性模型进行滤波[8]。

EKF算法的非线性系统方程为

式中，为非线性状态方程；为非线性输出方程。状态矩阵和观测矩阵如下：

EKF的递推公式如下：

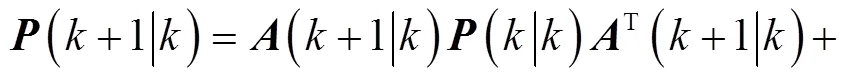
(+1) （15）

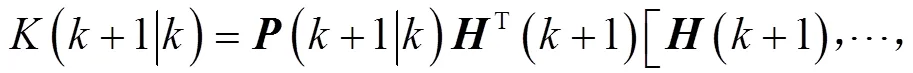
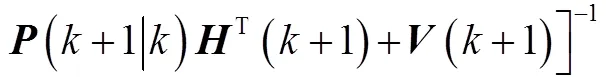
式中，为状态变量的协方差矩阵；为卡尔曼增益；、分别为系统噪声和观测噪声的协方差矩阵。

2.2 基于EKF的SOC估算

根据前文所述的EKF算法原理，结合式（6）、式（7）和式（10）、式（11），得到EKF算法的电池一阶RC等效电路的状态方程如下：

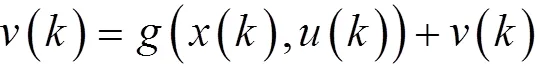
系统状态变量为

状态方程的系数矩阵为

观测方程系数矩阵为

式中，oc()为时刻的开路电压；(-1)为将-1时刻预测的值当作时刻的输入。

3 参数辨识

锂电池的充放电过程是非线性的，电池模型中的各个参数难以通过理论分析获得。一阶RC等效电路模型需要辨识的参数有oc、1、1、0。为了辨识这些参数，对电池进行完整的充放电试验，并采集记录数据[9-11]。

试验对象：额定电压3.7 V，放电截止电压 2.85 V，充电截止电压4.2 V，额定容量27 A·h的锂电池，试验温度为25 ℃。试验系统的部件有PC机、数据采集卡、电子负载等组成。试验步骤如下：

1）在试验前，使用电子负载将电池剩余电量放空，至电池电压为2.85 V。

2）对电池进行先恒流后恒压的方式充满电，直至电压达到4.2 V，电池的SOC为1。

3）对电池进行放电容量测试，通过电子负载以1C进行放电，当电池SOC达到0.1时，停止放电，静置半小时，减小电压变化的影响。

4）重复步骤2）－步骤3）的过程，直到SOC为0。

通过以上试验可以得到参数oc的辨识，以0.1为间隔得到电池电压（Open Circuit Voltage, OCV）与剩余电量SOC的关系曲线OVC-SOC，利用MATLAB的工具Curve Fiting进行拟合，得到结果，如图2所示。同时利用最小二乘法求出各个元件参数的值，如表1所示。

表1 一阶RC等效电路模型参数表

图2 OVC-SOC关系曲线

4 验证分析

在进行了分析、试验和算法推导等过程的基础之上，使用MATLAB软件编写基于EKF算法的SOC估算程序，并进行仿真，电池SOC估算结果如图3所示，其中估计值是指根据算法估算的SOC值，试验值是指根据上述试验获得的SOC值，两者误差如图4所示。

图3 EKF滤波算法SOC结果

图4 电池SOC的估计误差

在开始阶段误差较大为EKF算法在执行时，电池SOC的初始值与试验值相差较大所致。当电池SOC小于0.3时，试验值与估计值较大，但误差控制在3%以内，提高了SOC估算精度，使EKF的估计值更接近真实模拟值，收敛性更好。

5 结论

本文通过建立一阶RC等效模型电路，根据基尔霍夫电压电流定律，建立电路模型的状态空间方程。同时，利用电池充放电的试验数据，进行参数辨识，得到OVC-SOC的关系曲线。最后利用MATLAB软件进行仿真验证，结果表明，EKF算法下的SOC估算结果与真实值接近，误差控制在3%以内，可以较好地对电池剩余电量进行预测。

[1] 欧阳明高.2020全球新能源汽车前沿及创新技术[J].高科技与产业化,2021,27(1):38-40.

[2] 刘志聪,张彦会,王君琦.锂离子电池SOC估算技术进展综述[J].汽车零部件,2022(12):91-95.

[3] 张小利.锂电池荷电状态估计及其管理系统设计[D].合肥:合肥工业大学,2021.

[4] ZHOU W L,ZHENG Y P,PAN Z J,et al.Review on the Battery Model and SOC Estimation Method[J].Proce- sses,2021,9(9):1685.

[5] 谭必蓉,杜建华,叶祥虎,等.基于模型的锂离子电池SOC估计方法综述[J].储能科学与技术,2023,12(6): 1995-2010.

[6] 黄英.卡尔曼滤波法估算电池系统荷电状态[J].汽车实用技术,2021,46(11):6-9.

[7] 晏晓锋.基于卡尔曼滤波的三元锂电池SOC估算研究[D].桂林:桂林电子科技大学,2022.

[8] 曹正鑫.基于改进的卡尔曼滤波算法的电机参数估计[D].南京:南京邮电大学,2021.

[9] 李田丰,易映萍.电动汽车用锂离子电池模型参数辨识研究[J].软件导刊,2021,20(10):117-123.

[10] 李晓锋.基于MATLAB的锂离子电池SOC相关参数辨识[J].电工材料,2021(5):25-28,34.

[11] 刘志聪,张彦会.锂离子电池参数辨识及荷电状态的估算[J].储能科学与技术,2022,11(11):3613-3622.

Power Battery SOC Estimation Based on Extended Kalman Filter

PAN Zhengjun1, YUAN Xingyou1, DENG Feihu1, YUE Shan1, XU Xia2

( 1.Jinken College of Technology, Nanjing 211156, China; 2.Changzhou Transportation Technician College, Changzhou 213147, China )

Kalman filter (KF) is an optimal estimation method based on minimum variance estimation, which is suitable for linear systems. However, on-board power batteries have strong nonlinear characteristics during actual operation. The estimation kalman filter (EKF) is obtained by improving the estimation kalman filter. This problem can be solved satisfactorily. Taking ternary lithium battery as the research object, this paper establishes a first-order RC equivalent circuit model as the basic battery model. Based on the experimental data of charge and discharge of lithium battery, the relationship curve of voltage and state of charge (SOC), OVC-SOC, is obtained by using MATLAB fitting. The least square method is used for parameter identification, and the EKF algorithm is used for real-time estimation of power battery SOC.

Power battery; First order RC; EKF; SOC estimation

U469.72

A

1671-7988(2023)22-23-05

10.16638/j.cnki.1671-7988.2023.022.005

潘正军（1993－），男，硕士，讲师，研究方向为新能源汽车技术，E-mail:1137656476@qq.com。

金肯职业技术学院2023年度科学研究项目（JKKY202304）；江苏省高职院校青年教师企业实践培训项目（2023QYSJ050）。