三维打印GP1不锈钢动态剪切力学性能研究*

□ 任 豪 □ 周刚毅 □ 董新龙 □ 付应乾 □ 舒 旗

1.宁波大学 冲击与安全工程教育部重点实验室 浙江宁波 315211 2.宁波大学 机械工程与力学学院 浙江宁波 315211

1 研究背景

自20世纪90年代三维打印技术发展以来,三维打印材料从高分子材料发展到金属粉末材料,使三维打印技术在航空航天、军事、汽车制造等领域有广泛应用。这些领域对三维打印材料有特殊要求,如零部件需要具备耐冲击、耐挤压、抗变形等性能,使三维打印材料的力学性能成为研究重点。

目前,研究人员重点关注工艺参数优化对准静态力学性能的影响[4-5],三维打印成型件动态加载方面的研究还比较少。因此,有必要对三维打印成型件的动态力学性能开展研究。Ullah等[6]采用激光选区熔化工艺制备TC4钛合金蜂窝芯材,通过力学试验表明剪切和压缩性能都超过了航空航天标准。Song等[7]采用三维打印技术研究304L不锈钢的动态拉伸和压缩力学性能,在应变小于0.3时,压缩的屈服应力和流动应力相对较高;还分析了在应变率相近时,三维打印技术制备的试样比传统铸造制备的试样有更高的屈服强度和流动应力,断裂伸长率则较低。在实际应用中,三维打印成型件会受到冲击载荷,因此,有必要对三维打印成型件的动态力学性能开展研究。在研究剪切加载时,研究人员以往采用圆柱试样的压缩[8]、薄壁管的扭转[9]、动态帽型试样的剪切[9-10]等,来研究动态剪切性能。Meyer等[10]、Hartmann等[11]最早提出圆柱帽型剪切试验。圆柱帽型试样有对称和加载方便等优点,但是有一个很大的缺点,就是加工比较困难,精度达不到要求,并且对圆柱帽型试样剪切区域的观测比较困难。对此,Clos等[12]提出一种扁平帽型试样,可以直接对其剪切区域进行测试。然而,上述圆柱帽型剪切试样和扁平帽型剪切试样都有相同的问题,就是在受迫剪切时由于试样结构变形等原因,导致试样剪切区域不是纯剪切状态,只能定性讨论,难以得到相应的等效应力应变曲线。

笔者采用分离式霍普金森压杆对GP1不锈钢材料扁平板帽型剪切试样开展研究,采用超高速相机记录其剪切破坏过程,利用数字图像相关法测试剪切区域的应力演化,分析材料的剪切变形,得到等效应力应变曲线,并对其进行分析。

2 试验方法

试验采用直径为14.5 mm的分离式霍普金森压杆对GP1不锈钢扁平帽型剪切试样进行动态加载,试样设置在输入杆和输出杆之间,试验设置如图1所示。试验采用不同长度的子弹,分别为200 mm、300 mm、400 mm、500 mm,并采用不同的子弹速度进行。

根据霍普金森一维应力波分析,利用通过入射杆和透射杆上的应变片来测试应变值,从而可得到试样剪切区域动态剪切力F(t)及试样压缩位移ΔD(t)[13],分别为:

F(t)=AbarEbarεt(t)

(1)

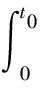
(2)

式中:t为时间;εi(t)为入射波信号;εr(t)为反射波信号;Abar为霍普金森压杆横截面积;Ebar为霍普金森压杆弹性模量;C0为弹性波速。

在动态加载试验分析中,通常假设试样的剪切区是单纯的剪切应力状态,由此得到试样剪切区域剪应力τxy[14-15],为:

τxy=F(t)/As

(3)

式中:As为试样剪切面积。

进一步分析,假设剪切区域的变形为均匀分布,并且在试样设计时预留剪切变形宽度Δw,那么可以获得近似的工程剪切应变Υtheo[16],为:

Υtheo=α≈tanα=ΔD/Δw

(4)

试验加载原理如图2所示。在子弹撞击入射杆时,划圈部分为剪切区域,w1为试样上端宽度,w2为开口宽度,h为剪切区域高度。如果假设试样的剪切区域是单纯的剪切应力状态,那么可以按式(3)计算得到剪切区域的应力。

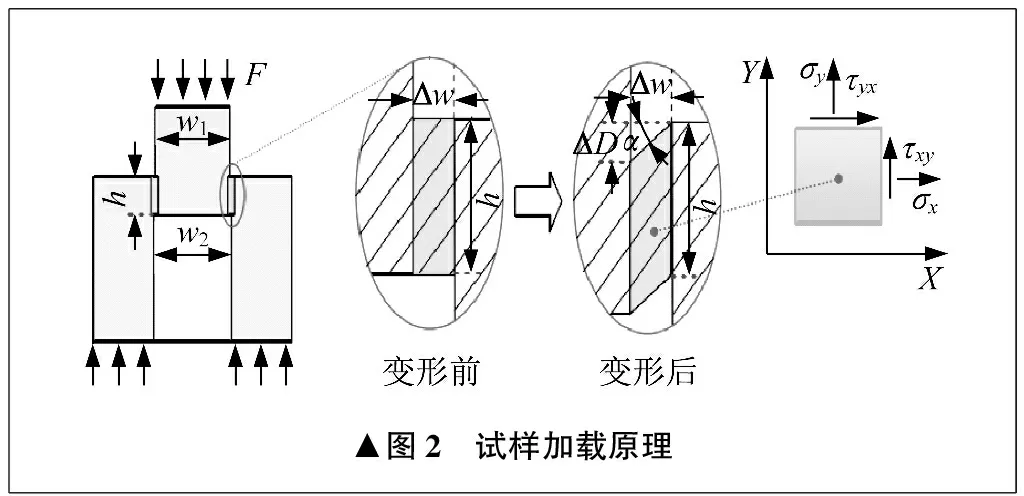
在传统帽型试样实际加载过程中,由于试样结构的影响,试样的剪切区域不是单纯只有剪切,会出现正应力σx、σy,按式(3)、式(4)计算得到的仅仅是微元体相应面上的剪应力分量。在试验加载过程中,剪切变形的宽度不会和预留剪切变形宽度相等[17],所以需要将试样设计为扁平帽型。

3 试样准备

试验选用GP1不锈钢粉末,化学成分及质量分数为锰0.61%、钢2.69%、硅0.63%、碳0.05%、铬17.54%、铁74.54%、镍4.36%。原始GP1不锈钢粉末的扫描电子显微镜形貌如图3所示,平均粒径为35 μm。试样采用三维打印设备制备,制备过程采用振镜扫描,工艺参数为扫描速度1 000 mm/s、铺粉速度80 mm/s、激光功率400 W、层厚20 μm、预热温度80 ℃。制备过程中,采用氮气保护,防止氧化[18]。

扁平帽型剪切试样的设计尺寸如图4所示,H1为2.2 mm,H2为7 mm,H3为2.2 mm,L1为3 mm,L2为3.2 mm,h为2 mm,Δw为0.6 mm。试样整体厚度为5 mm。为了使剪切区域变形均匀,剪切区域的起始处和终端处都设计为圆角。

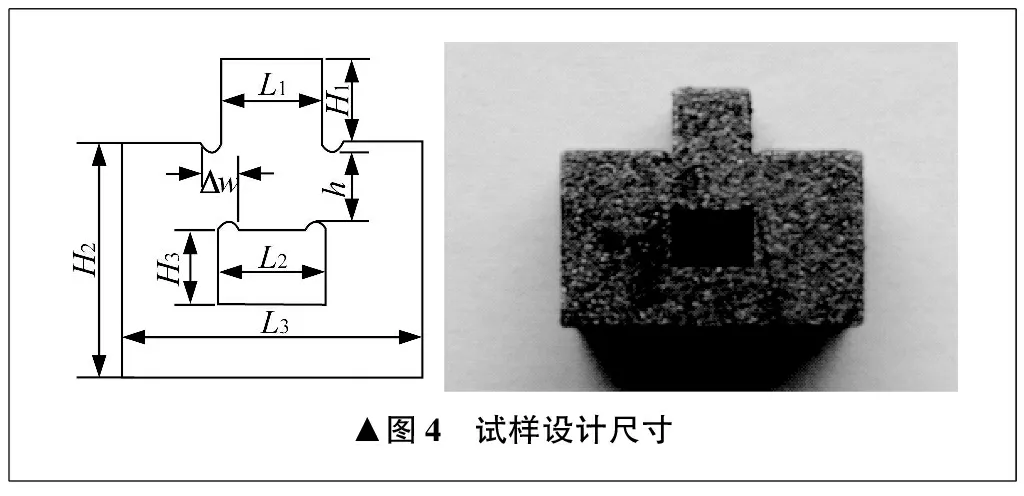
成型后,扁平帽型剪切试样如图5所示,横截面与纵截面微观金相组织如图6所示。由图6可知,无论是横截面还是纵截面,材料致密性良好,无孔洞等无明显缺陷。

针对剪切区域复杂的应力状态,对所设计的扁平帽型剪切试样采用莫尔圆图解法[19]。复杂应力状态可用莫尔圆表示,如图7所示。σ1、σ2、σ3均为应力状态的主应力,可见AB长度对应σ1-σ3。将AB看作为等边三角形的一条边,做等边三角形ABC,连接D、C,可以得到DC对应等效应力σe为:

(5)

应力状态下的最大剪切应力。文献[20]推导出,在发生小变形时,等效应变εe为:

(6)

从而可以得到能够反映材料特征的等效应力应变曲线。

4 试验结果

分离式霍普金森压杆动态剪切试验得到GP1不锈钢试样一组典型入射波、反射波、透射波电压信号,如图8所示。可见,在试验过程中,子弹长为300 mm,撞击速度为5.8 m/s时,从75 μs开始,入射波持续加载,反射波和透射波出现下降,表明在时间为75 μs时扁平帽型剪切试样开始出现破坏,直到90 μs时发生断裂。通过式(1)、式(2)得到动态应力位移曲线,如图9所示。当然,在试验加载过程中,试样剪切区域宽度是不断变化的,很难准确直接计算得到剪切应力应变曲线,剪切区域的应变不容易通过试验得到。

子弹长度为300 mm,撞击速度为5.4 m/s时,采用数字图像相关法,分析剪应力、剪应变演化过程。试样剪应变云图如图10所示,可见试样剪切区域变形初期沿剪切方向均匀变形,随着压缩位移的增大,剪切区域宽度不断减小,直到发生集中断裂。

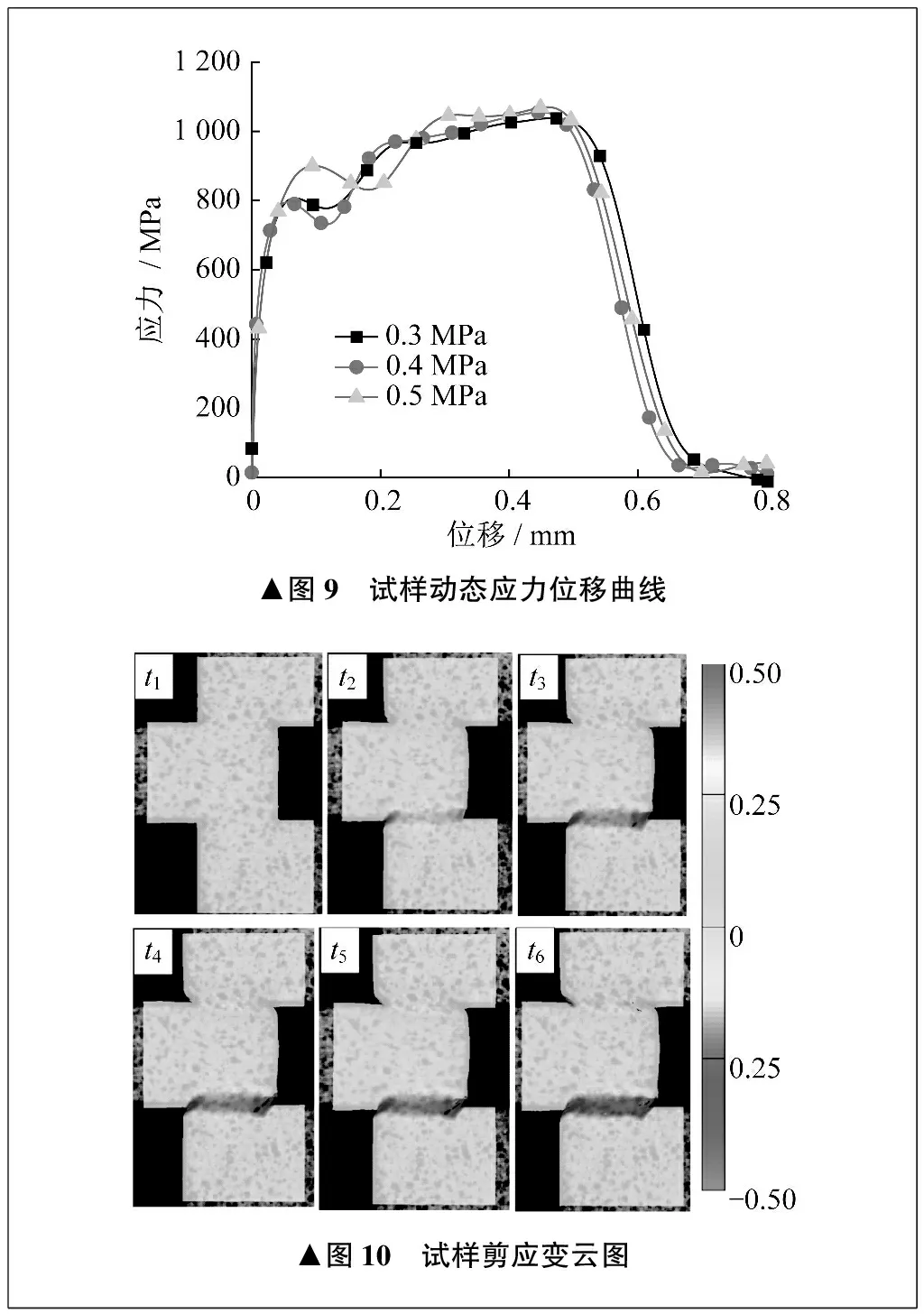
试样剪切应变和剪切应力时程曲线如图11所示。可见从t1到t4,剪切应力不断增大,剪切区域宽度不断减小,从t5开始发生剪切破坏,直到t6完全破坏,剪切应力减小为0。

试样沿剪切方向剪切区域各点剪切应变时程曲线如图12所示,可见剪切区域在整个加载过程中近似均匀,由此在试验过程中取中点来表征剪切区域的平均应变。

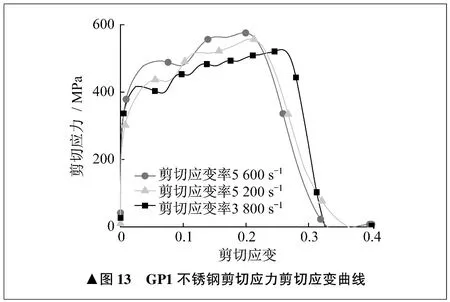
GP1不锈钢不同剪切应变率的剪切应力剪切应变曲线如图13所示,可见随着剪切应变率的增大,屈服强度与流动应力都提高;随着剪切应变率的增大,应变硬化强度提高;剪切应变率达到5 600 s-1时,还没有观察到应变软化特征。

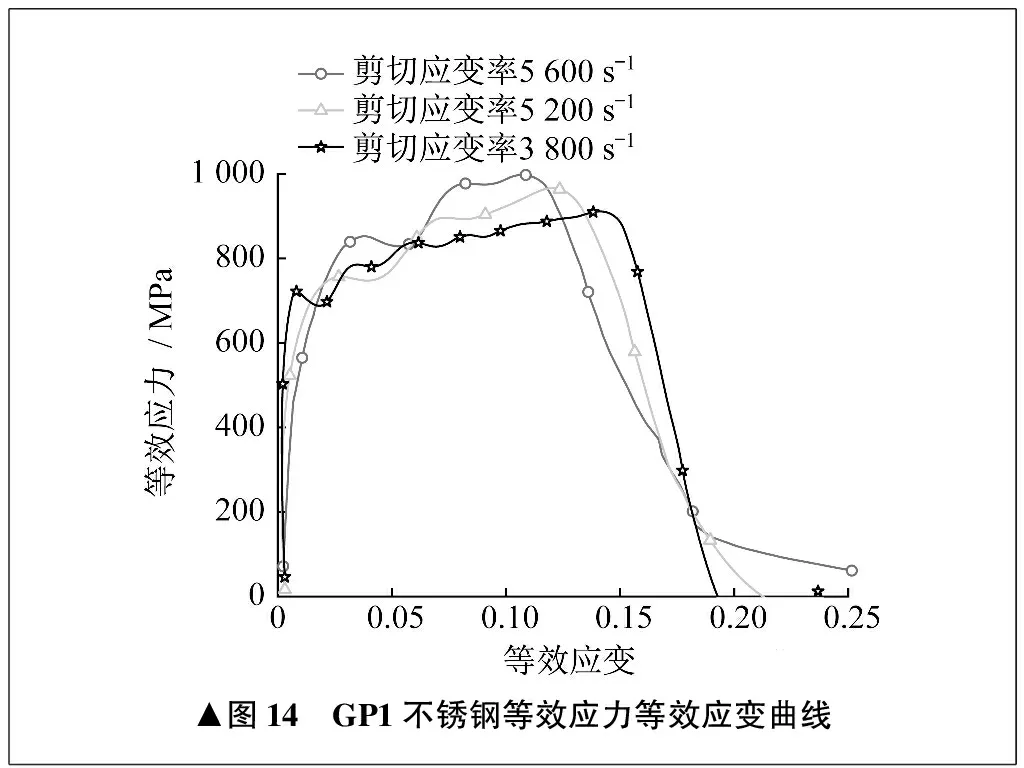
通过式(3)、式(5)处理得到等效应力等效应变曲线。GP1不锈钢不同剪切应变率的等效应力等效应变曲线如图14所示,可见存在明显的应变率效应。在剪切应变率3 800～5 600 s-1范围内,随着剪切应变率的增大,应变强化明显。在剪切应变率3 800～5 600 s-1范围内,随着剪切应变率的增大,屈服强度提高。

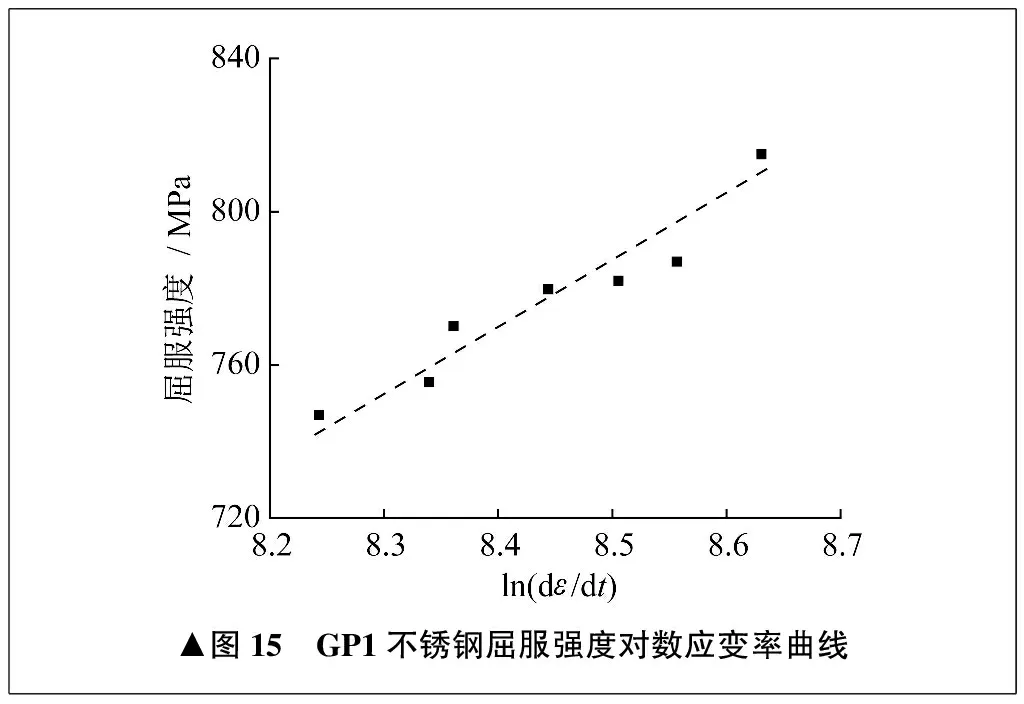
GP1不锈钢动态屈服强度对数应变率曲线如图15所示,可见屈服强度与对数应变率接近线性关系,剪切应变率在3 800～5 600 s-1范围内,随着剪切应变率的增大,屈服强度线性提高,从3 800 s-1时的747 MPa提高到5 600 s-1时的815 MPa。

为了衡量三维打印GP1不锈钢的应变速率强化效应,用应变率敏感因数λ来表征[21],为:

(7)

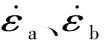
通过式(7)可以计算得到GP1不锈钢动态剪切应变率敏感因数为186。

5 结束语

通过三维打印工艺制备扁平帽型剪切试样,采用分离式霍普金森压杆对其开展动态剪切力学性能试验研究。由于加载过程中试样剪切区域宽度是不断变化的,无法给出应变,因此在试验中,采用超高速相机记录动态变形过程,采用数字图像相关法直接对试样剪切区域剪切应变分布及演化过程进行分析,得到剪切应变,进而得到剪切应力剪切应变曲线、等效应力等效应变曲线。试验结果显示,三维打印GP1不锈钢剪切加载状态下,应力应变曲线具有一定的应变率效应,动态屈服强度与对数应变率成线性关系,应变率敏感因数为186。