基于双层强化学习的多功能雷达认知干扰决策方法

廖艳苹，谢榕浩

哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

具有认知功能的多功能雷达(multi-function radar, MFR)可以感知作战环境，并根据作战环境的变化动态调整作战方式[1]，能够实现多部传统雷达才能实现的功能，大大降低了运行和维护成本[2]，因此被广泛应用于各种军事用途。不同于传统雷达，MFR 工作状态灵活多变[3-4]，单一固定的传统干扰决策方法很难再对雷达方产生有效干扰[5]。为了对MFR 进行有效干扰，国内外学者提出了一系列干扰决策方法，根据是否具有自适应与自学习能力可以分为2 类[6]。第1 类是不具有自适应和自学习能力的传统干扰决策方法，该类方法未利用侦察信息，灵活度较低：文献[7]提出了基于多决策准则的干扰样式选择方法，将不同准则中选优次数最多的干扰样式确定为最佳干扰样式；文献[8]提出了基于博弈论的干扰决策方法，将雷达干扰与抗干扰的过程看作一个动态博弈的过程。第2 类是具有自适应和自学习能力的智能干扰[9]方法，该类方法利用了侦察信息，灵活度较高：文献[10]提出了一种基于部分可观测马尔可夫决策过程(partially observable Markov decision process，POMDP)的干扰决策技术，在对方雷达工作策略未知的前提下，干扰方依旧可以做出较为有效的干扰决策；文献[11]设计了基于Q-Learning[12]算法的雷达对抗过程，使得干扰系统能够自主学习针对性强的干扰策略；文献[13]提出了基于先验知识的MFR 智能干扰决策算法，相对于传统的Q-Learning 算法，极大地提高了算法的收敛速率。

上述方法为MFR 的干扰决策奠定了基础，尤其是第2 类方法成为目前的研究热点。然而在实际环境中，MFR 模型往往比较复杂，也难以获得关于MFR 工作状态转移的正确先验知识[14]。针对这一问题，本文提出一种基于双层强化学习的MFR 认知干扰决策算法，通过双层强化学习，克服复杂模型和错误先验知识给传统强化学习算法带来的困难，改善干扰决策收敛效果。仿真实验证明了本算法的有效性，这对于强化学习在智能干扰决策中的运用具有重要意义。

1 强化学习与认知对抗

强化学习[15]（reinforcement learning, RL）不要求预先给定任何数据，而是通过接收环境对动作的奖励（反馈）获得学习信息并更新模型参数，然后改进行动策略，最终适应环境，如图1 所示。强化学习的特点使它可以满足无人化的现代军事需求[16]，用于解决认知对抗问题。具体来说，令干扰机为智能体，MFR 为环境，干扰机通过与MFR 交互学习获得雷达方信息，改进干扰策略，达到干扰目的，如图2 所示。

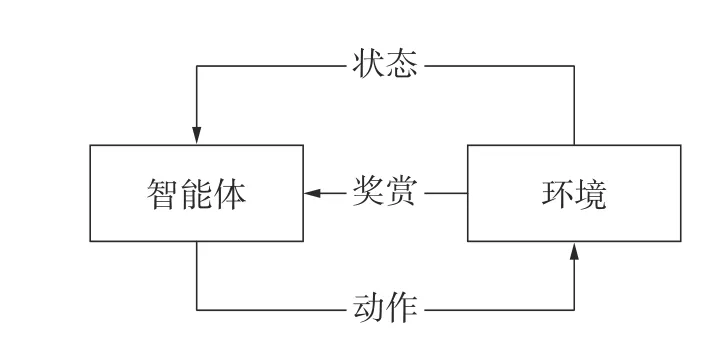
图1 强化学习过程

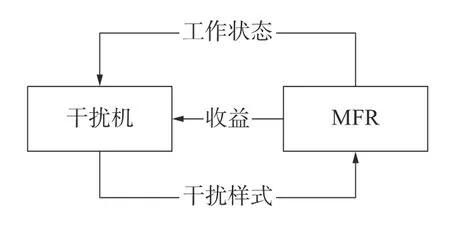
图2 强化学习解决认知对抗问题

2 双层强化学习干扰决策算法

2.1 双层强化学习算法框架

在先验知识正确且MFR 工作状态转移模型简单的情况下，文献[13]提出的基于先验知识的收益函数塑造方法确实可以加快Q-Learning 算法的收敛速度。但在非合作对抗中，一方面，MFR 从初始工作状态转移到目标工作状态经历的中间工作状态信息，即先验知识很难保证正确；另一方面，MFR 从初始工作状态转移到目标工作状态可能有多条干扰决策路径长度相近的策略，在这种情况下，现有的单层强化学习算法无法收敛至最优干扰策略，甚至会被错误先验知识误导而做出错误决策。

以图3 为例，与简单MFR 模型相比，复杂MFR 模型中干扰决策路径长度小于10 的干扰策略数量从1 条增加到了8 条以上。现实中，MFR 模型的复杂程度可能更高。

图3 简单MFR 模型（左）与复杂MFR 模型（右）对比

在有错误先验知识的情况下，为了消除错误先验知识对干扰决策的误导，提高算法挖掘信息和适应复杂MFR 模型的能力，本文提出基于双层强化学习的MFR 干扰决策算法。该算法分为2 层强化学习：第1 层强化学习检验先验知识是否正确，如果正确，则跳过第2 层强化学习直接根据Q矩阵生成最优干扰策略，如果不正确，则将发现的最短决策路径信息作为新的先验知识加入到第2 层强化学习；第2 层强化学习使用第1 层强化学习更新的先验知识，进行基于先验知识的Q-Learning 算法，根据Q矩阵生成最优干扰策略。算法流程如图4 所示。

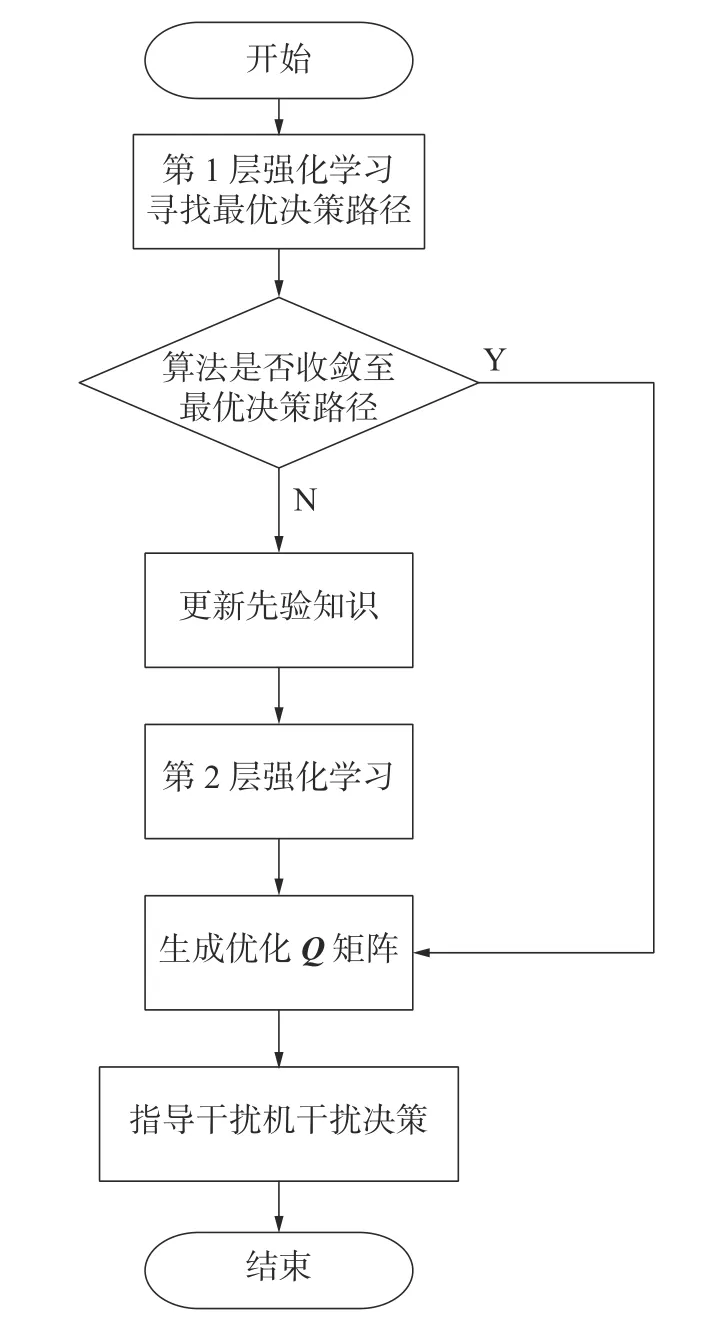
图4 双层强化学习算法

2.2 Q-Learning 算法

本文提出的基于双层强化学习干扰决策算法以Q-Learning 算法为基础。在Q-Learning 算法中，令状态集S为MFR 的工作状态集合，动作集A为干扰方的干扰样式集合，p为MFR 的工作状态转移概率，R为干扰效果收益函数，V为MFR 工作状态价值函数，Q为MFR 工作状态-干扰方干扰样式价值函数[17]。在MFR 认知干扰决策中，干扰方的目的是采取干扰措施之后MFR 尽快转移至低威胁状态或者战术需要的目标状态。干扰决策算法的目标是计算得到一个收敛且正确的Q矩阵，干扰方再根据Q矩阵进行干扰决策，找到一条决策路径最短的干扰策略，作为最优干扰策略。

定义 π为MDP 的行动策略，策略 π决定了价值函数V和Q的大小，最优策略 π*就是使每个状态s的状态价值Vπ*(s)最大的策略：

在Q-Learning 算法中，智能体采取动作之后，更新迭代状态-动作价值函数Q(s,a)：

式中：s和a分别为当前时刻智能体的状态和采取的动作；s′为下一时刻智能体的状态；r(s,a)为智能体状态为s时，采取动作a获 得的收益； α为学习率，α ∈(0,1) ； γ为折扣因子，代表未来收益相对当前收益的重要程度，γ ∈(0,1)。

2.3 改进Q-Learning 算法的动作选择策略

在Q-Learning 算法的每一次迭代中，智能体利用ε-贪婪策略进行动作选择，即以 ε的概率从动作集A中随机选择一个动作，以1-ε的概率选择Q值最大的动作。现有Q-Learning 算法都是以固定的 ε值进行动作选择，导致算法探索知识的能力和利用知识的能力不能够达到最佳的平衡，无法满足双层强化学习算法的任务需求，为了强化双层强化学习算法探索知识和利用知识的能力，提高干扰决策效率，需要根据每一层强化学习的任务对动作选择策略进行改进。

1）提高第1 层强化学习的知识探索能力。为了保证干扰决策的实时性，第1 层强化学习要在尽可能短的时间内确认最优决策路径，检验先验知识的正确性。定义达到干扰目标的最短决策路径为最优决策路径，第1 层强化学习的动作选择策略要使得最短决策路径出现一定次数耗费的时间最少：

式中：Nbest为最短决策路径出现次数；Nc为一个正整数，代表确认最短决策路径有效的次数下限；Tcheck(ε)为最短决策路径出现次数达到Nc次(Nbest=Nc)所耗费的时间，Tcheck(ε)是与探索率ε有关的函数，该最小化问题通过参数寻优实验解决。

2）提高第2 层强化学习的知识利用能力。经过第1 层强化学习，算法已经获得了正确的先验知识。第2 层强化学习的目的是算法收敛，为了提高算法收敛速度，令探索率 随着算法逐渐收敛而自适应地减小，降低探索信息能力，提高利用知识能力：

ε

式中： ε0是初始探索率，Ngood是较短决策路径(收敛步数不超过10)出现次数。

3 仿真实验

用马尔可夫模型(Markov decision process，MDP)代替隐马尔可夫模型[18]对MFR 的脉冲序列信号进行建模，将MFR 系统建模为一个有限状态机。MFR 在受到干扰方施加的干扰之后，会发生工作状态转移，用转移矩阵定量描述MFR 模型工作状态转移的概率，为了体现非合作对抗的性质，将转移概率以随机矩阵的形式给出：式中：c为干扰样式库中的一种干扰样式，不同干扰样式对应不同的转移矩阵；pc

ij为MFR 在干扰样式c作用下从状态i转移到状态j的概率，且对于任意为MFR 工作状态总数。

假设MFR 工作状态总数为50 个，状态转移关系如图5 所示，干扰机干扰样式总数为9 个。

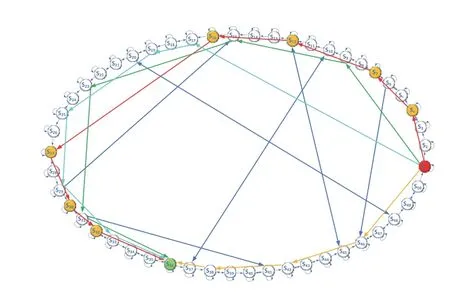
图5 MFR 状态转移关系

MFR 状态转移矩阵根据MFR 状态转移关系随机生成，矩阵数量为9 个，矩阵大小为50×50。MFR 初始状态sinit为s1，干扰方设立的目标状态saim为s36。干扰方通过与MFR 交互学习，优化Q矩阵，减小雷达从初始状态转移到目标状态所需的决策步数。定义决策步数最短的干扰策略为最优干扰策略。

3.1 错误先验知识对单层强化学习算法的影响

假设干扰方在干扰决策前被提供的错误先验知识为se=[s4,s7,s12,s16,s27,s30,s32]，基于错误先验知识的单层强化学习算法干扰决策结果如图6所示。

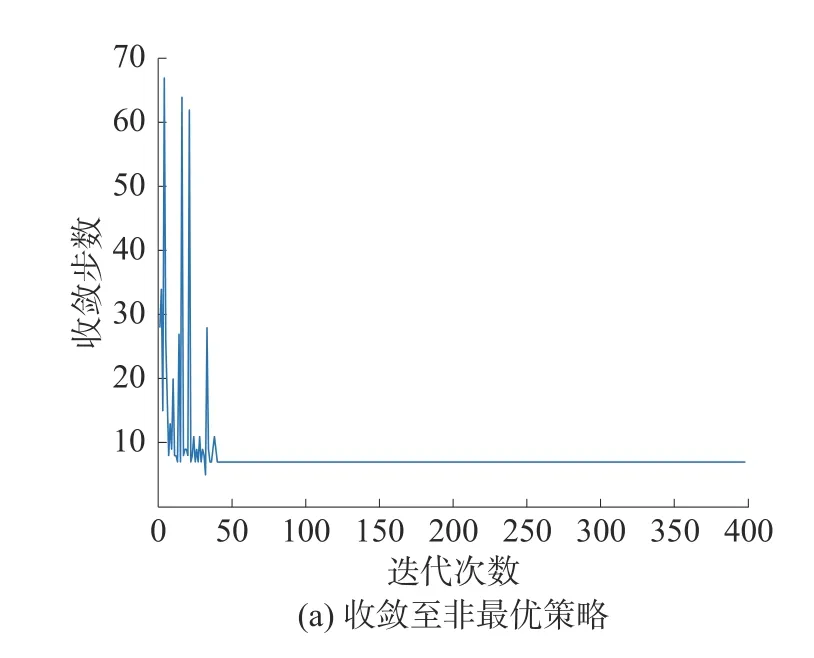
如图6(a)所示，在错误先验知识的误导下，传统单层强化学习算法收敛至决策的路径为s1→s4→s7→s12→s16→s27→s30→s32→s36， 路径长度为8 步，非最优干扰策略；如图6(b)所示，在错误先验知识的干扰下，传统单层强化学习算法无法收敛。在错误先验知识情况下，传统单层强化学习算法进行100 次蒙特卡洛实验，算法收敛情况统计如表1 所示。

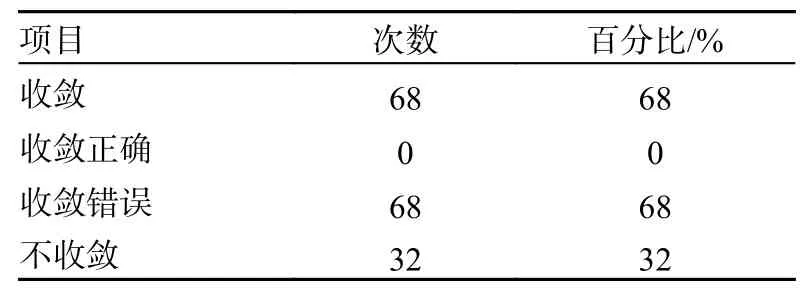
表1 传统单层强化学习算法实验结果统计

由仿真结果可知，如果先验知识错误，则现有单层强化学习算法无法求解得到最优干扰策略。本文提出的双层强化学习算法通过任务分层可以解决这一问题。

3.2 第1 层强化学习：寻找最短决策路径

探索率ε ∈(0,1]，以步长0.01 取值，进行参数寻优实验，每个参数下进行50 次蒙特卡洛实验，每次蒙特卡洛实验进行400 个回合强化学习，分别对最短决策路径出现次数和最短决策路径最早出现时间（回合）求平均值，得到仿真结果如图7和图8 所示。

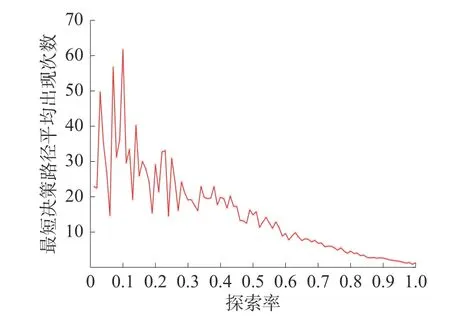
图7 探索率与最短决策路径出现次数

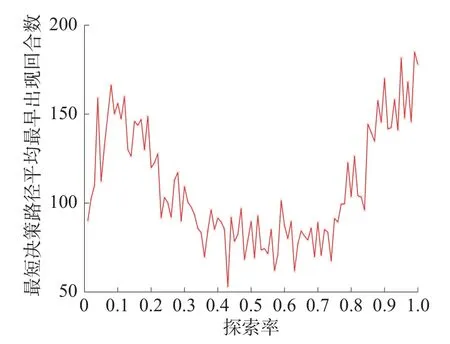
图8 探索率与最短决策路径最早出现时间（回合）

由图7 可知，探索率增大则最短决策路径出现次数减少。由图8 可知，探索率过大或过小都会导致寻找到最短决策路径的回合数过大、时间过长。因此，根据式(1)，要在较短时间内找到较多最短决策路径，设置探索率的选择区间为[0.4,0.7]。

选择ε=0.43进行第1 层强化学习，进行第1 层强化学习后寻找到的最短决策路径为s1→s46→s42→s38→s36，比基于错误先验知识寻找到的决策路径s1→s4→s7→s12→s16→s27→s30→s32→s36更快，与图5 的MFR 状态转移关系相符合，证明了第1 层强化学习在错误先验知识的情况下能够找到最优干扰策略。根据双层强化学习算法，将第1 层强化学习找到的最短决策路径信息s1→s46→s42→s38→s36作为正确先验知识更新se，则更新后的正确先验知识se=[s38,s42,s46]。

3.3 第2 层强化学习：生成Q 矩阵

假设sinit=s49、saim=s36，因为初始状态不是s1了，由第1 层强化学习过程可知，需要将s1也加入到先验知识中去，即se=[s1,s38,s42,s46]。设置学习率α=0.01、折扣因子γ=0.95，研究不同探索率ε对第2 层强化学习算法收敛的影响。式(2)设置4 种不同探索率 ε，它们对算法收敛的影响如图9 所示。

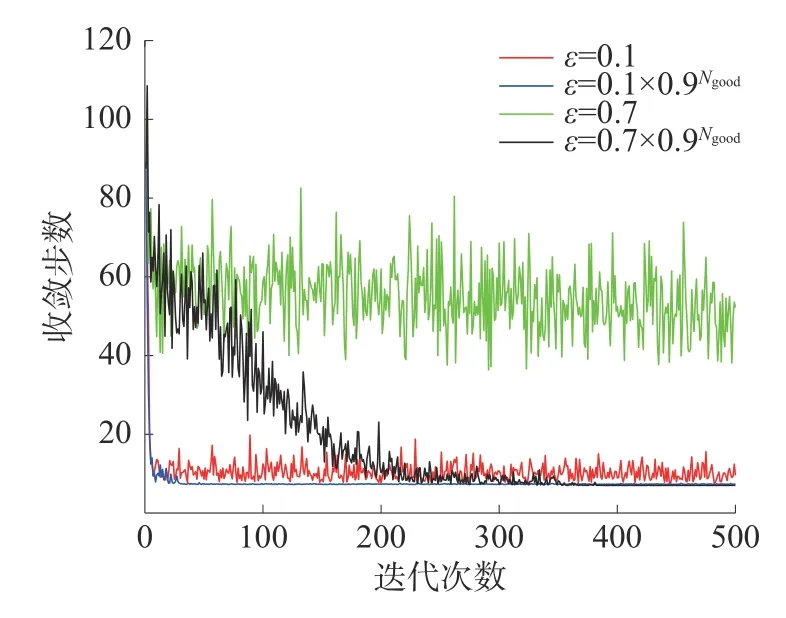
图9 探索率变化情况对收敛效果的影响

式中Ngood是较短决策路径(收敛步数不超过10)出现的次数。

由图9 仿真结果对比可知，较小的且随着算法逐渐收敛而自适应减小的探索率可以使算法更快收敛。因此，本文将探索率 ε设置为ε=0.1×0.9Ngood。

基于先验知识的Q-Learning 算法，通过改造收益函数可以加快算法收敛速度[13]，利用先验知识改造收益函数R：

式中：Nae为正整数；a＞0，代表正向激励；se为MFR 从初始工作状态转移到目标工作状态需要经历的中间工作状态，即先验知识；b＞0，代表先验知识带来的附加收益大小，可根据实际情况调整。

定义收敛正确率为算法收敛到最优干扰策略的次数占实验总次数的比率。令式(3)中a=1、b=2，智能体到达目标状态saim的收益Nae与到达中间状态se的收益1 之间的倍数关系Nae对收敛正确率的影响如图10 所示。

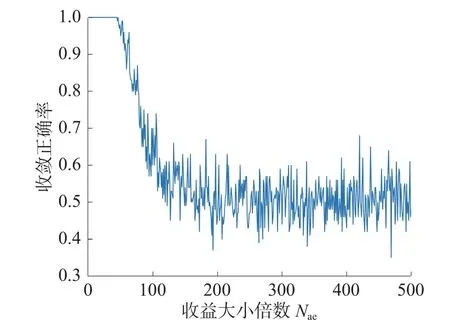
Nae图10 与收敛正确率的关系

由仿真结果可知，Nae取值太大会造成收敛正确率下降，为了保证算法正确收敛，提高干扰决策正确率，Nae的取值区间应为[1,44]。选择Nae=20进行第2 层强化学习，最终基于先验知识的高收敛正确率收益函数塑造为

设置学习率α=0.01、折扣因子γ=0.95、探索率ε=0.1×0.9Ngood，每次实验进行400 个回合的强化学习，一共进行50 次实验，收敛步数取平均值。不同收益函数对应算法的收敛效果如图11所示。

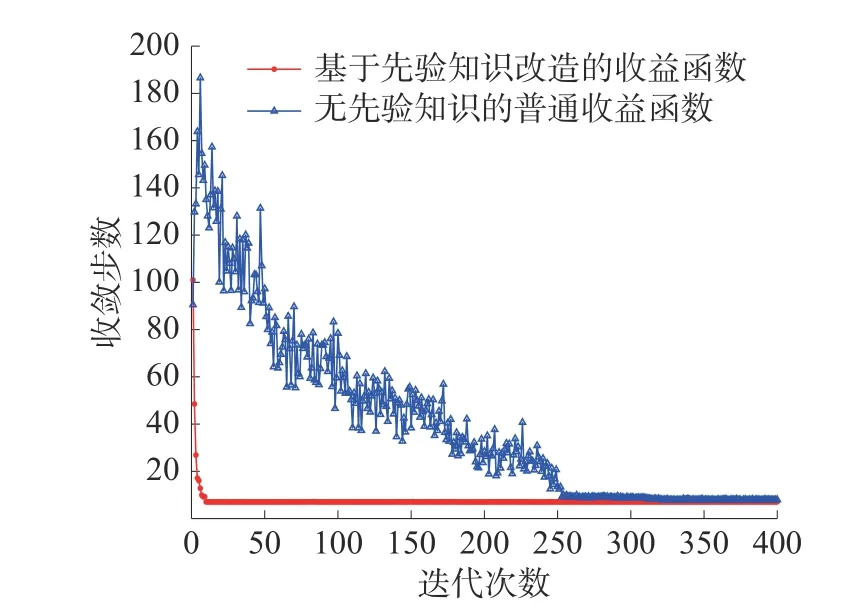
图11 不同收益函数收敛效果对比

基于先验知识的第2 层强化学习算法最终收敛于最短决策路径s49→s50→s1→s46→s42→s38→s36，步数为6，与图5 的MFR 状态转移关系相符合，证明了最短决策路径的正确性。由图11 收敛曲线可知，基于先验知识的算法经过8 次迭代即收敛，而无先验知识的算法经过250 次迭代才收敛，证明了基于先验知识的QLearning 算法通过改造收益函数可以大大提高收敛速度。

算法生成的Q矩阵如表2 所示。表2 列出了Q矩阵中和本次决策过程有关的数据，该矩阵代表强化学习学习到的知识。算法收敛之后，在每次干扰决策时，干扰方根据Q矩阵选择当前状态对应的Q值最大的干扰样式进行干扰。

由Q矩阵可知，MFR 工作状态为s49时，选择干扰样式5，记为a5；MFR 工作状态为s50时，选择干扰样式8，记为a8；MFR 工作状态为s1时，选择干扰样式6，记为a6；MFR 工作状态为s46时，选择干扰样式5，记为a5；MFR 工作状态为s42时，选择干扰样式2，记为a2；MFR 工作状态为s38时，选择干扰样式9，记为a9。

于是，根据Q矩阵，最终求得当sinit=s49，saim=s36时最优干扰策略为

核对MFR 状态转移矩阵P，验证式(4)所示的最优干扰策略是否正确。

由矩阵P1、P2、P3、P4、P5、P6、P7、P8、P9可得表3。

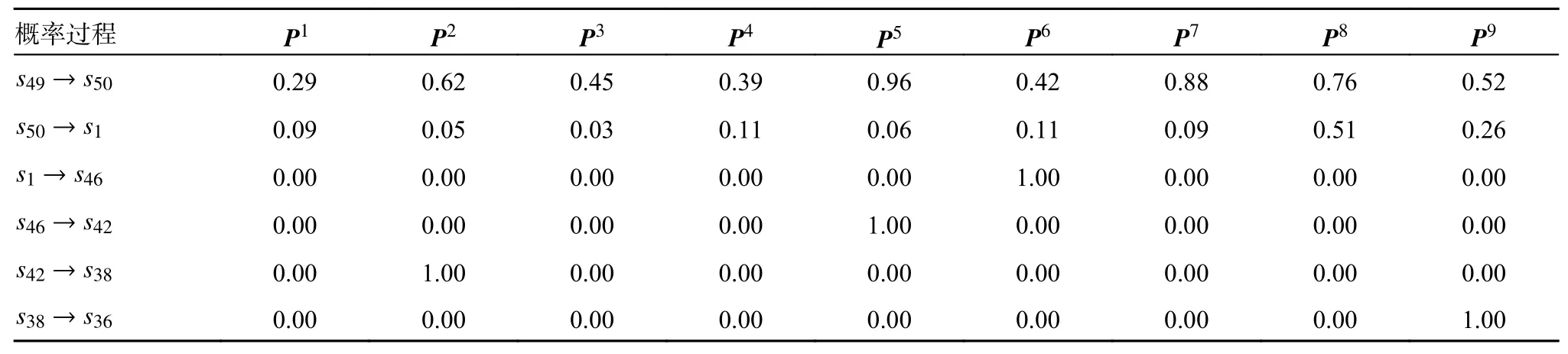
表3 不同干扰样式下MFR 状态转移概率

4 结论

本文提出了一种能够在复杂MFR 模型中克服错误先验知识误导的双层强化学习干扰决策算法。

1）该算法通过改进Q-Learning 算法的动作选择策略，提高干扰方挖掘信息和纠正错误先验知识的能力，克服错误先验知识对干扰决策的影响。

2）该算法通过研究收益函数大小与收敛正确率的关系，优化收益函数设置，提高算法收敛正确率。

3）该算法通过结合先验知识，加快算法收敛速度。

仿真实验表明，在错误先验知识情况下，面对复杂MFR 模型，该算法能够收敛至正确的最优干扰策略。动作选择策略和收益函数设置方法的改进，提高了MFR 认知干扰决策的效率和正确率。该算法能够有效增强认知干扰决策系统适应复杂电磁环境的能力。