基于目标PSO算法的工程项目优化研究
韩会宾
辽宁工业大学 经济管理学院,辽宁 锦州 121000
截至2020年, 我国建筑规模达到了26 397亿元, 同比增长6.2%, 工程建筑项目在我国经济发展中有着极为重要的地位. 伴随着国内经济增长、 工程技术革新, 国内工程项目建设正朝着规模化、 复杂化及高集成化方向发展, 工程项目多目标管理是保障项目有效开展的关键[1]. 在工程项目建设周期内, 需要保证工程满足相关施工要求, 包括项目工期、 项目质量、 项目成本、 环境要求等[2]. 由于工程项目目标相互作用并存在密切关联, 一个目标调整会给其他目标造成影响, 如何有效平衡各个项目管理目标成为工程项目建设的难点[3]. 因此, 对现有工程项目展开研究, 需满足工期、 降低成本并符合项目建设质量要求, 构建工程项目多目标优化模型. 工程项目属于多目标优化问题, 机器学习模型在处理此类问题上具备明显的优势, 如神经网络、 模拟退火、 群智算法等均能很好地处理此类问题[4]. 本文引入先进的PSO算法构建项目工程多目标求解模型, 同时采用最优位置策略对PSO模型的局部收敛进行优化, 从而实现对工程项目多目标问题的优化. 工程项目多目标优化问题的难点在于资源合理分配与目标平衡, 采用优化方法对工程项目多目标优化具有重要的参考价值.
1 基于目标PSO算法的工程项目优化模型构建
1.1 工程项目多目标优化模型构建
在工程项目建设中, 项目管理任务需要满足3大目标, 分别是工期、 质量与成本目标. 3个目标之间并不是相互独立的个体, 3者相互作用影响, 在实际工程项目管理中很难达到平衡. 因此, 需要将工期、 质量与成本作为优化目标构建工程项目优化模型, 从而实现对项目施工的有效管理, 并降低工程建设成本[5]. 工程项目多目标优化模型技术路线如图1所示.
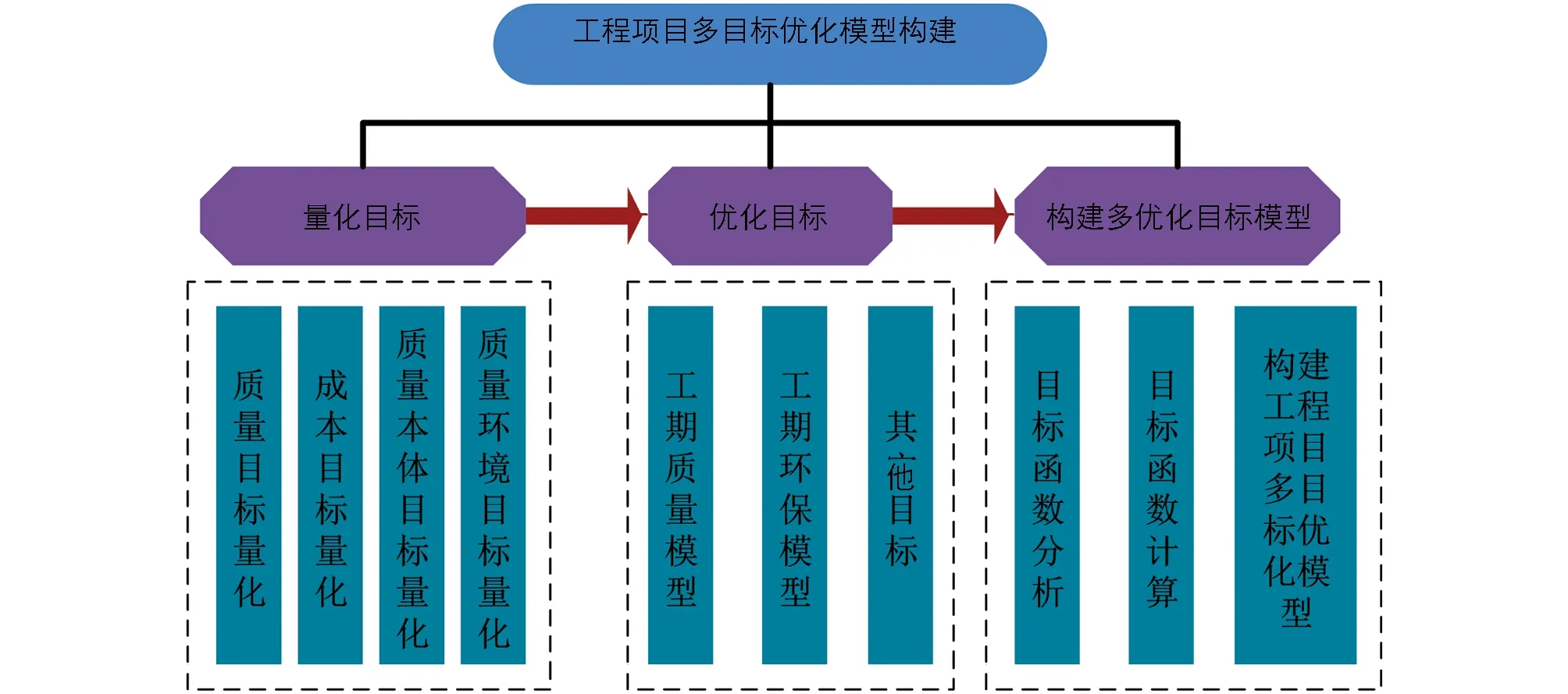
图1 工程项目多目标优化技术路线
工期目标指工程项目从规划至项目竣工所耗费的所有时间, 其中工程项目建设最长时间为项目建设工期[6]. 工程项目工期在建设期间受到内部与外部综合因素的影响, 为了更好地描述工期与项目的关系, 通常采用双代号网络构建工期模型[7]. 在网络计划中将不同路线赋予不同的施工时间, 并且持续时间最长的路线为工程项目总工期, 且作为网络关键线路. 为了方便工期模型构建, 假设项目按照规划路线顺利开展, 并且其余工序不管如何调整, 均不会对关键工序造成影响. 综合上述关系, 工期表达如式(1)所示.
(1)

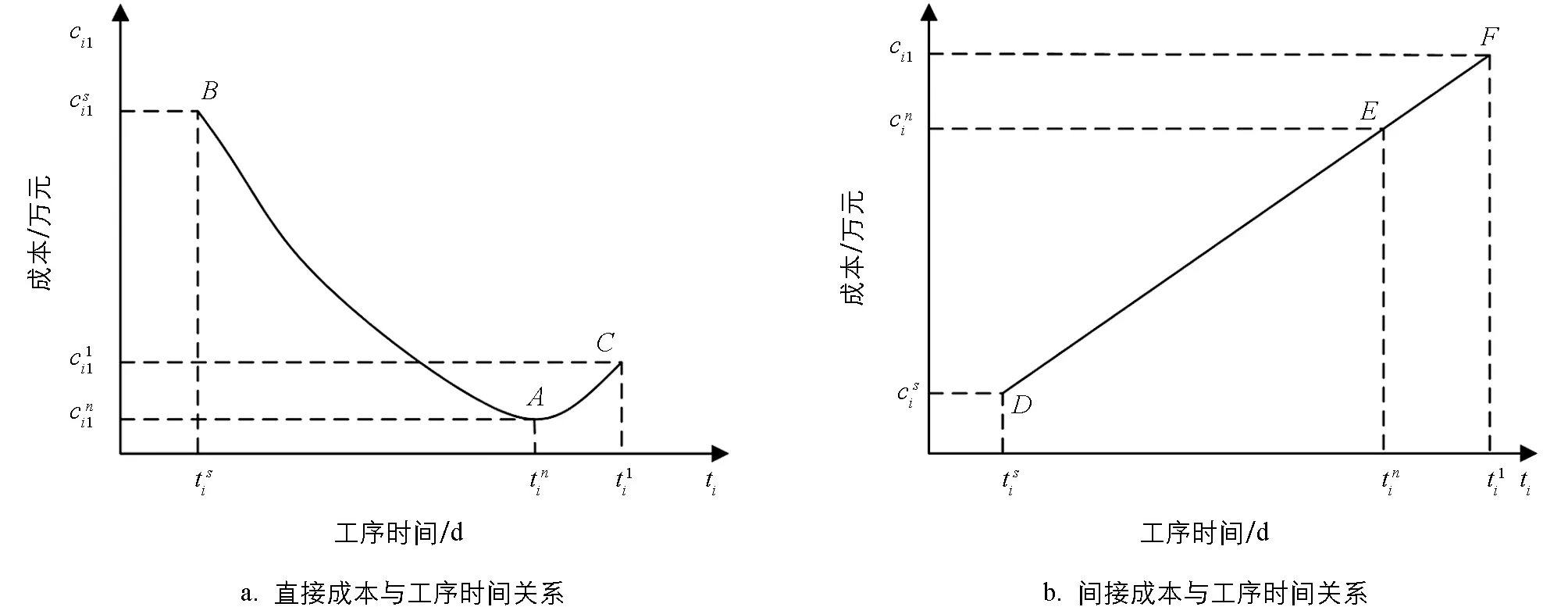
图2 成本与工序时间关系
(2)
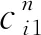
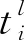
(3)
(4)
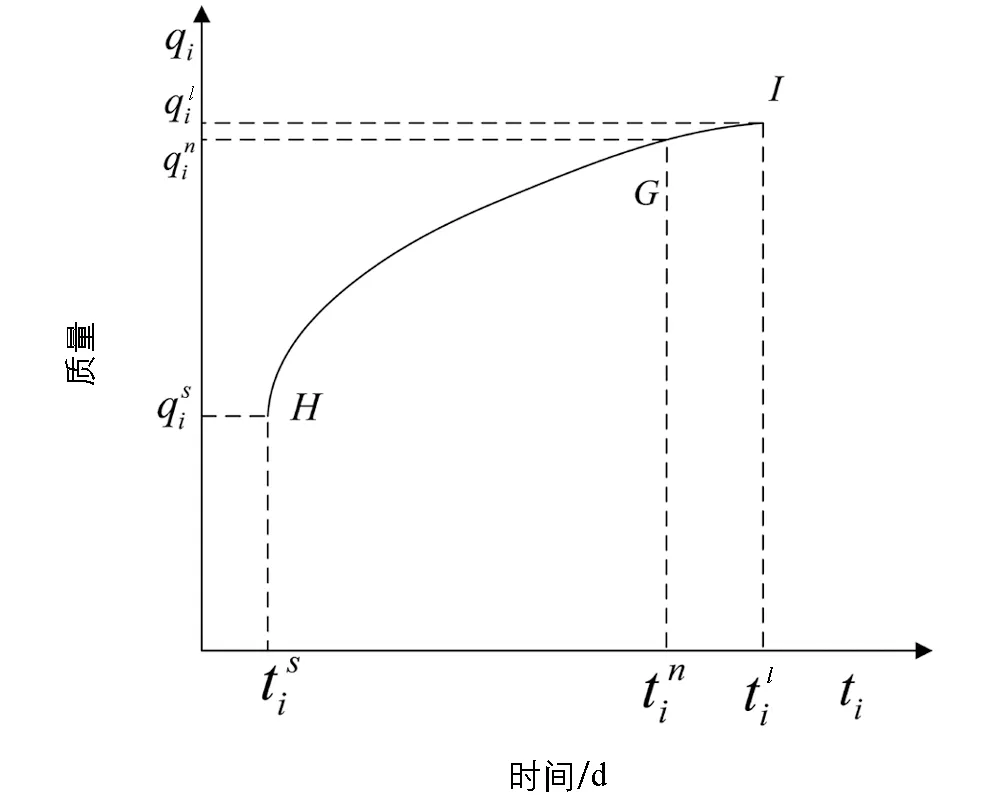
图工序时间内所对应的质量关系
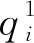
在对应的工序时间内, 工序应该达到的质量要求用函数表达如式(5)所示.
qil=ln(βiti+ai)
(5)
式(5)中,qil表示项目工序i质量,βi表示工序i的质量因素系数. 根据工序权重, 以工序质量计算整个工程项目本身质量如式(6)所示.
(6)
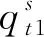
(7)
式(7)中,l表示项目区域影响系数,si表示项目对环境影响系数, 由专家团队打分得出. 工程项目内部环境质量如式(8)所示[15].
(8)
工程项目最终的工期-质量目标Q由工程项目本身质量和工程项目内部环境质量决定, 最终重量目标如式(9)所示.
Q=Q1+Q2
(9)
通过工期-成本模型与工期-质量模型, 构建工程项目多目标优化模型. 多目标优化模型最终目标是实现工期、 质量及成本3个目标的平衡[16]. 多目标优化模型约束条件包括工序时间、 工序质量、 区域经济系数等, 属于多组求解Pareto最优问题, 本文采用多目标粒子群算法来求解问题.
1.2 基于PSO算法的工程项目求解模型构建
工程项目多目标求解需要平衡工期、 成本与质量3个目标要求, 在满足工程建设要求下使工程建设效益最佳. 多目标求解问题属于向量优化问题, 由多个约束和目标函数构成, 某个目标取得最优结果会使另外的目标质量下降[17]. 为方便求解多目标问题, 通常在研究中引入Pareto最优解思想, 并通过改进的粒子群(Particle Swarm Optimization, PSO)求解模型, 寻找工程项目多目标最优解. 将工程项目多个目标求解问题表示为minG, 则表达如式10所示[18].
s.t.gi(x)≤0,i=1,2,…,k
hj(x)=0,j=1,2,…,p
(10)
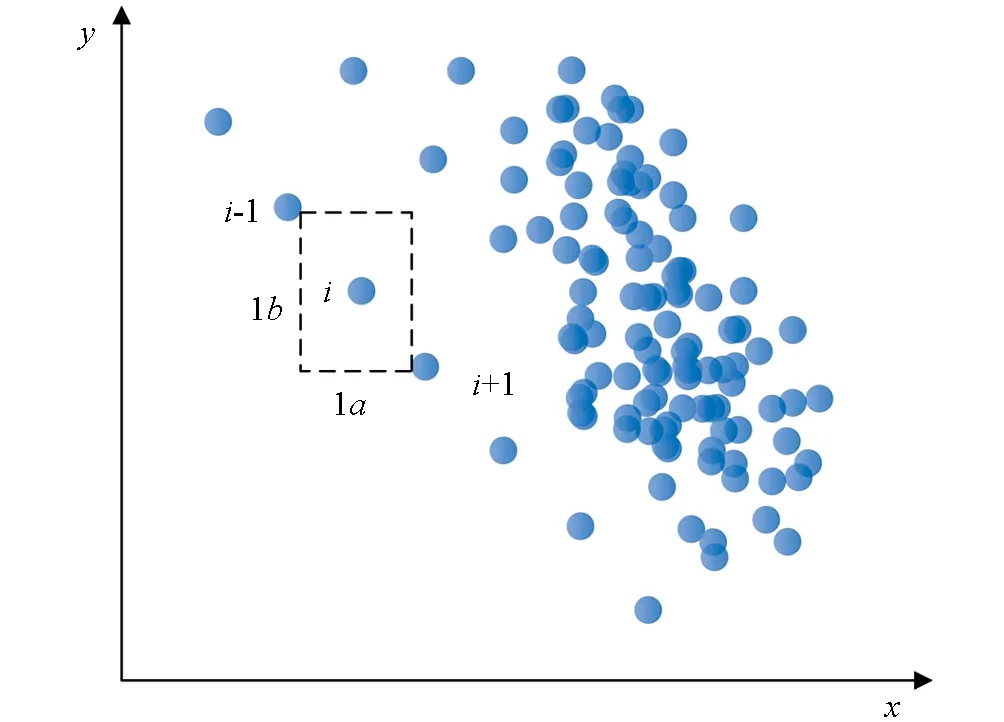
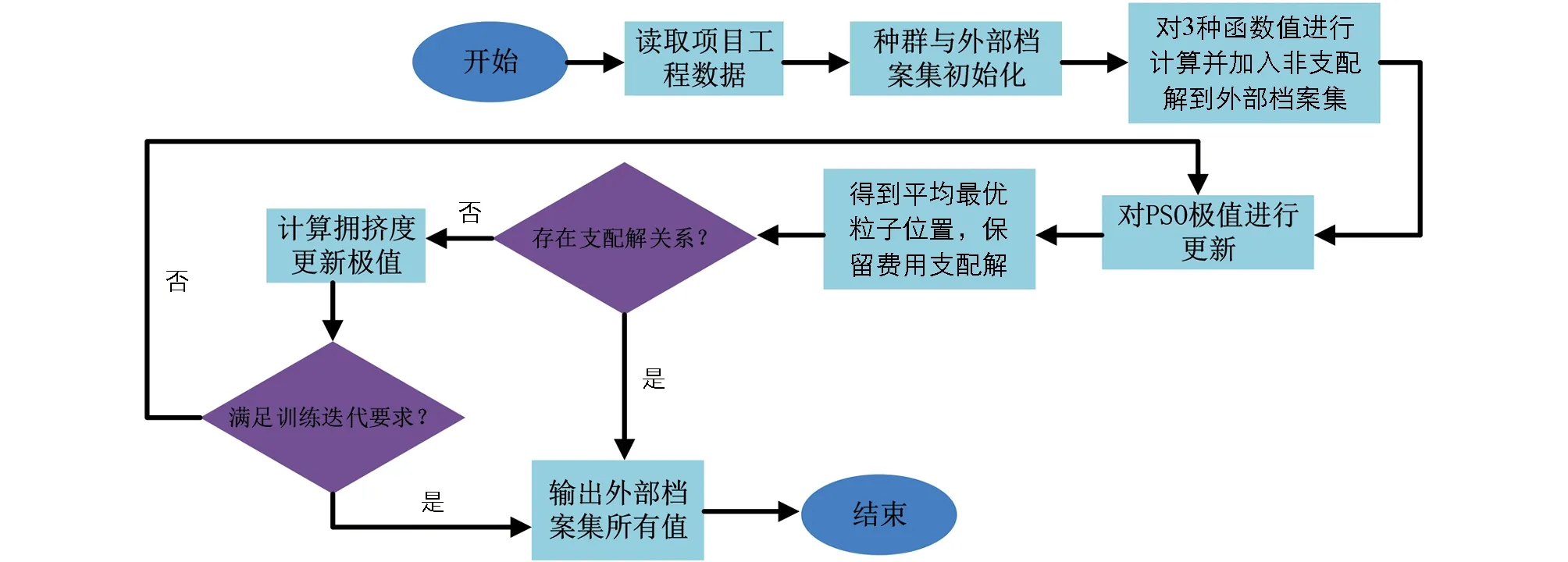
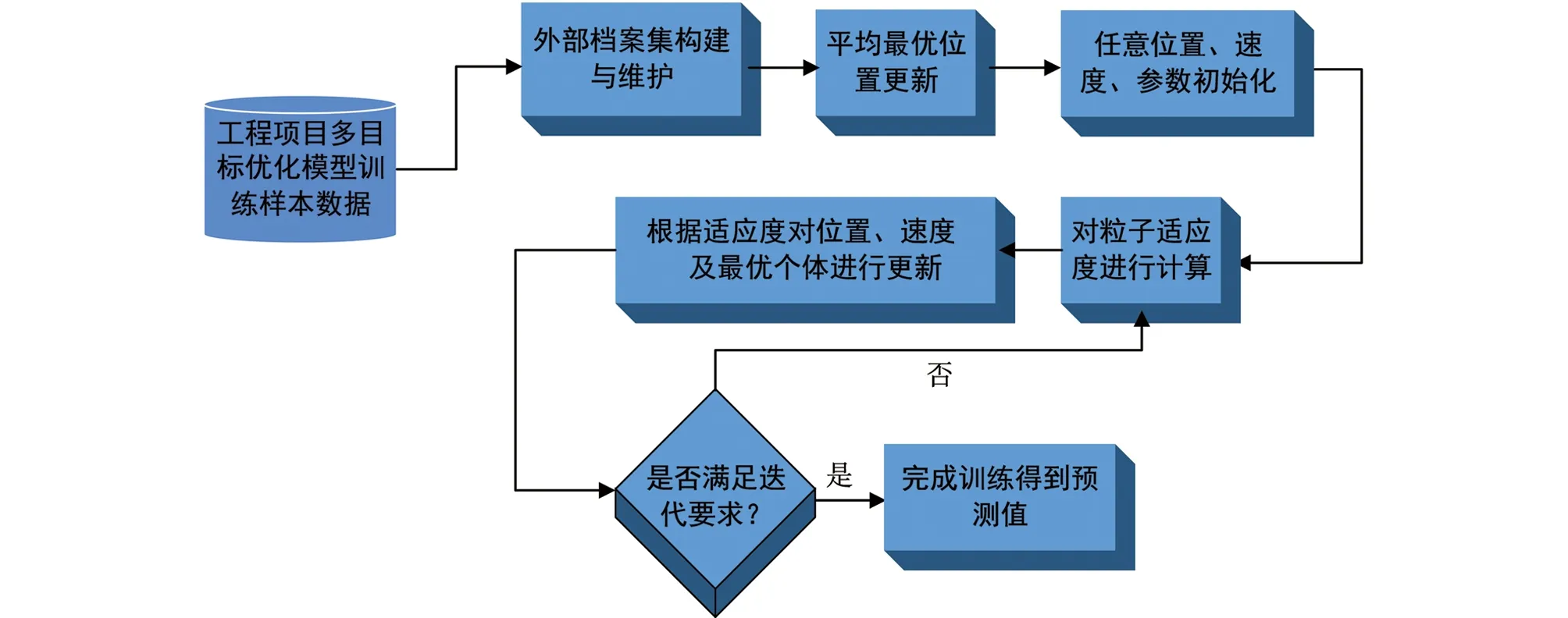
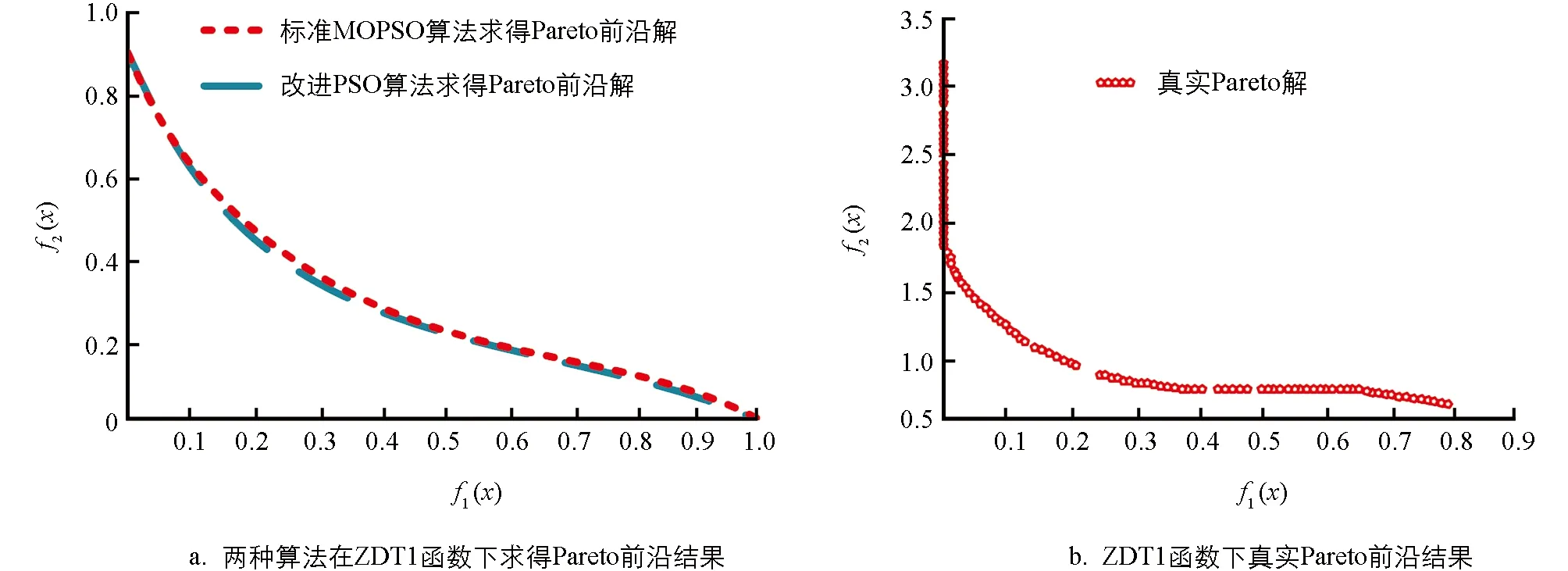
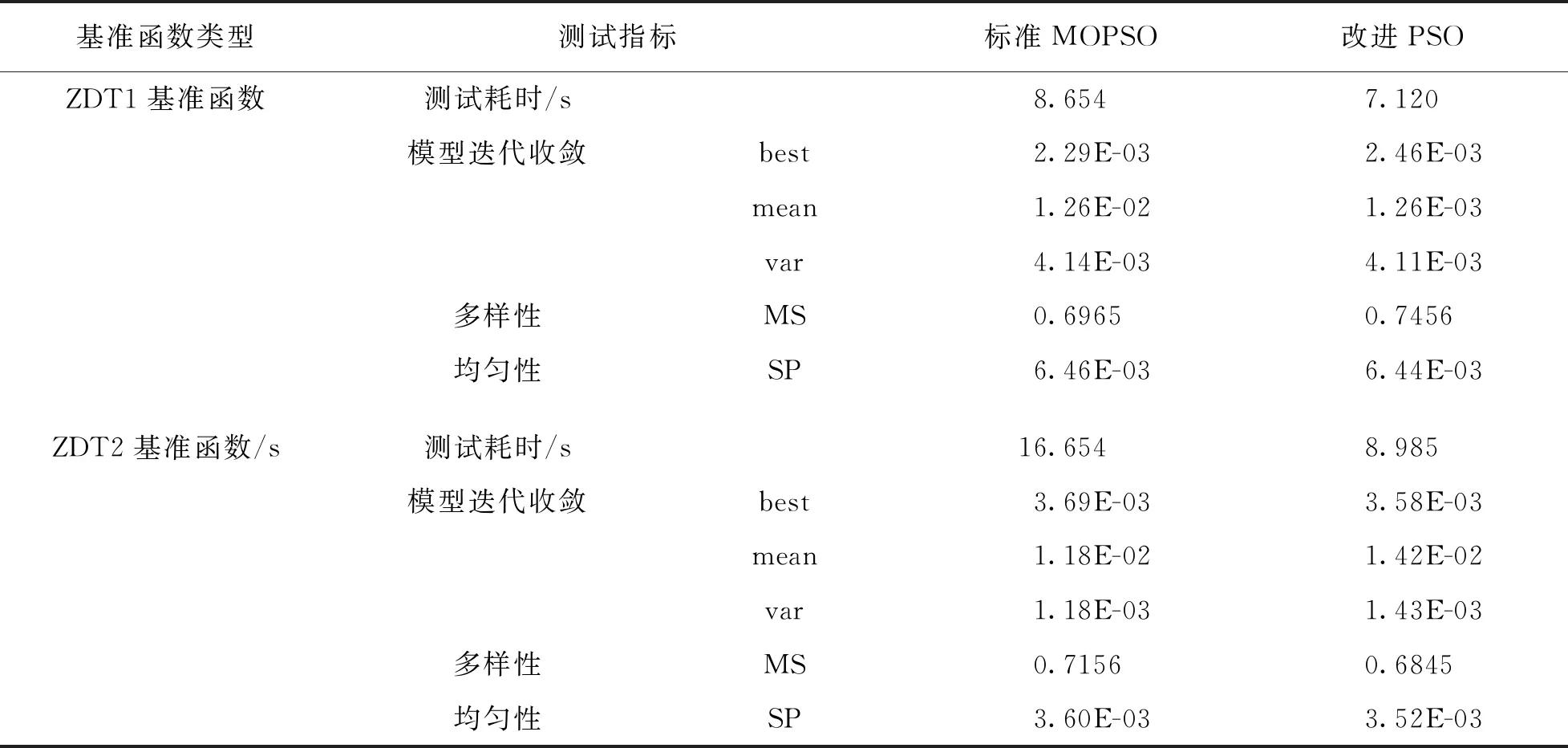
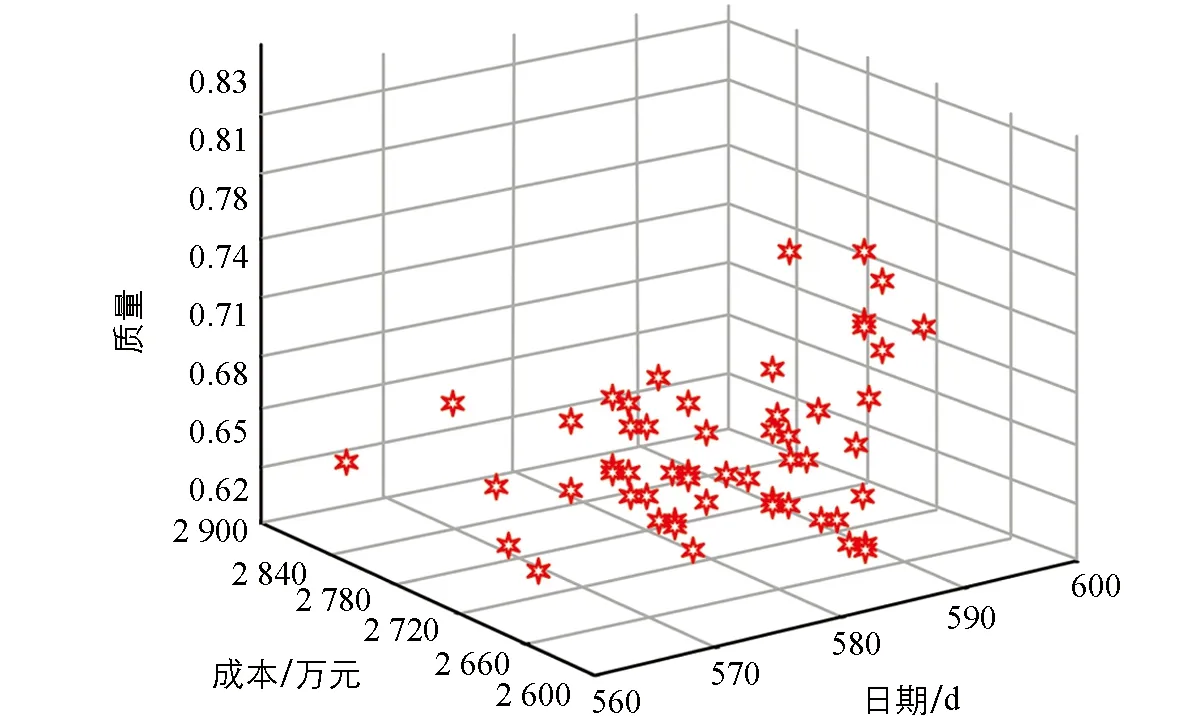
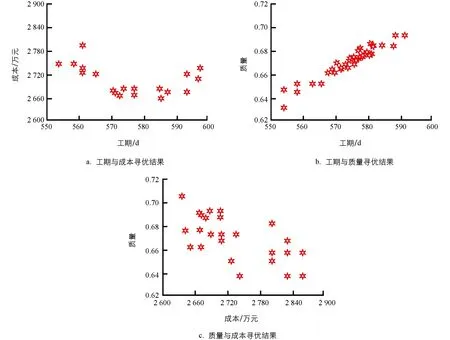
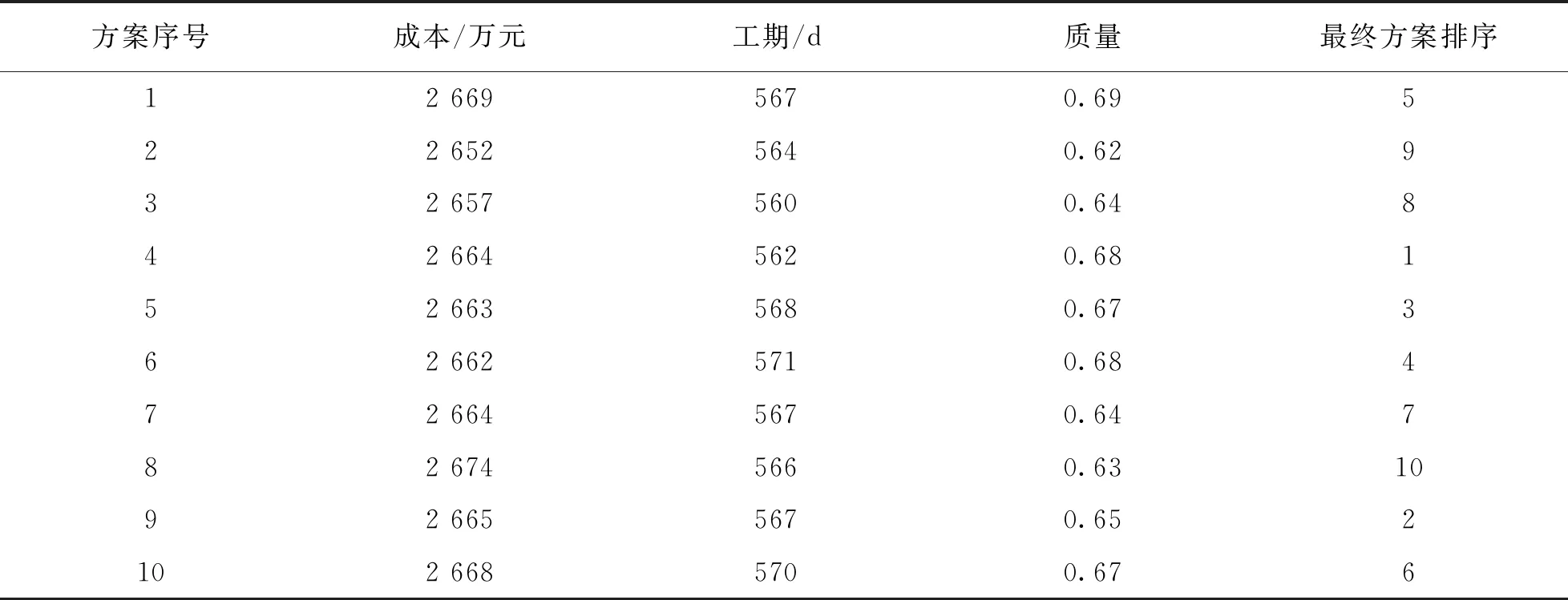
式(10)中,x1,x2,…,xn表示目标决策变量, 目标函数G由m各优化目标构成, 在工程项目建设中分为质量目标、 成本目标与工期目标.gi(x)≤0表示多目标函数不等式约束条件, 约束条件数量为k,hj(x)=0表示目标函数等式约束, 约束条件数量为p. 由于工程项目建设的复杂性与多变性, 在不同时间、 人员条件下工程项目的工期、 质量与成本均会受到影响. 为了保障函数目标求解最优, 采用Pareto支配关系表达工程项目多目标之间的优化关系[19], 其中定义Xbest属于多目标求解问题中的一个可行解, 为Pareto最优解. 同时, 在多目标中不存在可行解Xi,Xi PE={F(Xbest)=(f1(Xbest),f2(Xbest), …,fm(Xbest))T|Xbest∈p} (11) 式(11)中,f1(Xbest), …,fm(Xbest)表示可行解函数集,F(Xbest)表示目标解函数集. 在工程项目多目标问题求解中, 需要在约束范围内寻找工期、 质量与成本3大目标的最佳优化位置, 使工程项目3大优化目标平衡. 多目标优化求解问题如图4所示[21]. 图4 多目标问题求解示意图 在多目标求解中,f1至fm均为多目标问题的多个目标函数, 某个目标解函数值增高, 另外一个目标函数值必定降低, 在曲线A1至A2位置存在目标函数的Pareto最优解[22]. 传统多目标求解方法有约束法、 功效系数法等, 这些方法的问题处理思想是将多目标转化为单个目标进行问题优化, 虽然利于理解, 但无法平衡多个目标关系, 且计算复杂[23]. 工程项目多目标优化问题的难点在于对3大目标问题进行平衡, 质量、 成本与工期3者之间相互约束, 传统多目标求解思想主观性较强, 无法满足工程建设综合性优化要求[24]. 因此, 本文引入先进粒子群算法来构建PSO模型, 完成对工程项目多目标问题的求解. PSO算法属于一种群智优化算法, 该算法的思想以群体行为为基础, 通过粒子群体在一定范围内进行有序搜索, 从而寻找最佳的问题解. PSO算法在处理多目标优化问题、 分类问题及识别问题时具有良好的应用效果. 可以将粒子群理解为由多只鸟组成的鸟群, 每一个粒子表示一只觅食的鸟, 在粒子群中共有n只鸟. 粒子群中的每一只鸟会在同维度空间觅食, 每一只鸟会对搜索路线进行记忆并记录有食物的最佳位置. 同时, 鸟群搜寻食物的方向和距离与自身速度有关, 鸟群速度最终由同行鸟儿飞行经验决定[25]. 定义粒子在一个D维空间范围内进行搜索, 在该范围内第i个粒子群可以定义为m维向量, 表达如式(12)所示. xi=(xi1,xi2, …,xim)Ti=1,2,…,n (12) 式(12)中,xi表示第i个粒子在维度空间的位置信息. 为了方便粒子群搜索到有效的最优解值, 需要对粒子的搜索空间范围进行限制. 在D维区间范围内, 第i个粒子对应的最大边界位置为xmax, 对应的最大搜寻速度为vmax. 粒子在最大边界位置时, 最大飞行速度被限制为vmax, 粒子在维度空间飞行速度向量如式(13)所示. vi=(vi1,vi2, , …,vim)Ti=1,2,…,n (13) 式(13)中,vi1,vi2, , …,vim表示第i个粒子在不同位置的飞行速度. 为了对PSO算法的开发能力和搜寻效果进行平衡, 粒子群在飞行过程中需要对自身速度vi进行限制. 在vi取值较大时, 粒子群训练容易陷入全局最优解问题; 当vi取值较小时, 粒子群搜索性能提高, 但容易陷入局部最优解问题. 引入最优位置策略对PSO模型的训练效果进行优化, 避免模型陷入局部收敛问题. 在多目标PSO算法的每一次迭代更新中, 粒子均会对历史搜寻的最佳位置进行记忆, 即将粒子搜寻的最优解存储于外部档案内. 当训练中产生的非支配解i受到外部档案支配时, 档案集将保持原有状态[26]. 当外部档案集中有解受到新产生的非支配解支配时, 则产生的新支配解将取代原有档案内的解, 并对外部档案信息进行更新, 以这种更新方式将粒子群搜索的最优解进行记忆存储. 但在实际粒子群训练中, 外部档案集数量有限, 需要采用拥挤度计算式对档案集进行修剪. 拥挤度表示在某一种群内个体所在密度, 计算拥挤度距离原理如图5所示. 图5 计算拥挤度距离示意图 对相邻两粒子围成矩形顶点距离进行计算, 则粒子i此刻的拥挤距离如式(14)所示. li=la+lb (14) 式(14)中,la与lb表示两粒子所围成矩形的长与宽. 当外部档案集规模较小时, 对粒子群的拥挤距离进行计算, 并对较小拥挤距离的非支配解进行修剪, 以满足算法设置的迭代要求. PSO算法外部档案集更新与维护如图6所示. 图6 外部档案集更新与维护 传统PSO算法在更新全局最优粒子与个体最优粒子时, 粒子种群容易陷入粒子局部最优解问题, 停止寻找最优结果, 因此本文引入最优位置策略优化此问题, 计算粒子群个体最优位置如式(15)所示. (15) 式(15)中,Xibest表示第i粒子个体最优解,p表示粒子数量,D表示粒子维数. 对式(15)进行更新, 得到粒子更新后的位置如式(16)所示. (16) 式(16)中,b表示吸引因子,β表示扩张系数,t表示迭代训练次数,u表示速度与自变量比值范围. 改进后的PSO求解模型参数设置更少, 对全局训练效果进行了优化. PSO求解模型工作流程如图7所示. 图7 工程项目多目标求解模型工程流程 为了检验本文改进PSO算法的性能效果, 选择ZDT1、 ZDT2及Schaffer共3种基准函数进行算法性能训练. 测试平台为Windows 7, 显卡为英伟达GTX3070, 处理器为志强64核. 模型训练参数如表1所示. 选择压缩粒子群(Compressibility_Factor Particle Swarm Optimization, YSPSO)、 学习因子粒子群(Learning Factor Particle Swarm Optimization, LNCPSO)及权重粒子群(Adapting inertia Particle Swarm Optimization, APSO)这3种改进PSO算法作为基础模型. 在Schaffer基准函数下4种算法模型的训练结果如图8所示. 图8(a)与图8(b)分别为4种算法在Schaffer函数上的完整收敛结果与迭代初期收敛结果. 在图8(a)中, 4种算法模型在迭代20次内均取得收敛, 4种算法全局最优值均为0.002 5, 但4种算法的性能测试效果有明显差异, 改进PSO算法在迭代训练时误差最低, 误差值为3.154, APSO算法、 YSPSO算法、 LNCPSO算法误差值分别为6.896,5.985,5.865. 在图8(b)中, 展示了4种算法初期训练情况, 改进PSO算法能够在第6次迭代时趋于收敛, 取得最优适应度值与全局最优值, 相较于APSO算法、 YSPSO算法和LNCPSO算法, 收敛性能提升了37.65%,27.86%和17.65%. 由此可见, 改进PSO算法相较于另外3种算法拥有更出色的收敛效果. 同时, 在ZDT1基准函数下对改进PSO算法的前沿结果进行测试, 如图9所示. 图9 ZDT1基准函数下各算法求解得到的Pareto前沿结果 图9(a)为标准MOPSO算法和改进PSO算法求得的Pareto前沿结果, 其中红色虚线为标准MOPSO算法求得的Pareto前沿结果, 蓝色虚线为改进PSO算法求得的Pareto前沿结果. 由测试结果可知, 改进PSO算法与标准MOPSO算法求得的前沿结果接近. 图9(b)为函数真实的Pareto前沿结果, 改进PSO和标准MOPSO前沿结果与真实结果基本吻合, 但两种算法在训练效果中有明显不同, 如表2所示. 表2 两种基准函数的3类指标测试结果 根据表2测试结果可知, 在ZDT1基准函数与ZDT2基准函数中, 相较于标准的MOPSO算法, 改进PSO算法在训练时间、 迭代效果、 收敛性等指标中数值更低, 说明改进PSO算法综合性更好. 在ZDT1基准函数中, 标准MOPSO算法耗时为8.654 s, 改进PSO算法为7.120 s, 因此将改进算法应用于工程项目多目标求解具有良好的优越性. 选择某建筑工程项目为实验分析对象, 该建筑项目为高层商品房, 建筑面积为17 562.65 m2, 建筑项目地上共有30层, 地下共有2层. 整个工程项目建设工期为580 d, 工程建设合同价格为2 768.80万元. 在实际工程项目建设中, 需要满足每道工序建设质量要求, 验收合格方可进入下一道工序, 因此该项目要求质量高于0.65, 工程每天间接费用为0.28万元, 整个工程项目共有16道工序. 设置改进PSO算法迭代次数为200次, 对工程项目成本、 工期及质量3个目标进行测试, 如图10为工程项目多目标Pareto最优解测试结果. 图10 工程项目多目标Pareto最优解测试结果 图10为工程项目多目标最优解测试结果, 改进PSO模型在迭代训练200次后得到了50组Pareto最优解. 由测试图像分布结果来看, 最优解集主要集中于图像中轴线位置. 对单个目标寻优结果进行分析, 如图11所示. 图11 工程项目单个目标寻优测试结果 图11(a)为工期与成本模型寻优测试结果. 由结果可知, 工期在585 d后工程项目成本呈现出上升趋势, 同时在560~580 d范围内, 工程项目成本呈现出下降趋势. 工程需要缩短工期并降低工程项目成本, 因此最优解在570~580 d范围内. 图11(b)为工期与质量模型寻优测试结果. 由测试结果可知, 随着工期增加, 工程项目质量不断提高. 工程项目质量要求在0.65以上, 在满足工程项目质量标准前提下需要降低工程建设时间, 因此工期范围在565~572 d范围内. 图11(c)为质量与成本模型寻优结果. 质量需要高于0.65, 且工程项目成本最低, 结合工期与成本模型测试结果, 成本在2 660万元至2 670万元之间. 综合上述分析结果, 得到10组工程项目最终优化方案, 如表3所示. 表3 工程项目多目标优化最终目标值 表3为工程项目最终优化的目标结果. 由结果可知, 工期、 质量与成本是3个相互影响的目标, 根据工程项目建设要求选出了10组方案, 并对方案进行了排名. 最终选择方案4作为工程项目建设的最终优化方案, 其中工程建设成本为2 664万元, 相较于工程合同预算的2 768.80万, 成本下降了104.8万元; 工程项目建设目标周期为580 d, 优化后工程建设周期为562 d, 工程周期减少了18 d; 工程质量满足项目建设要求, 工程质量为0.68, 高于工程项目质量0.65. 由此可见, 本文所采用的工程项目多目标优化方案能在满足工程项目建设条件下, 对工程项目3大目标进行有效优化, 大幅度降低了工程建设成本与工程建设周期. 最终通过优化前后数据对比可知, 工程建设成本下降了3.785%, 工期缩短了3.103%, 有效提高了工程项目的建设效果. 在建筑工程领域, 多目标优化问题一直是工程项目建设的重点与难点. 由于工程项目建设的特殊性与复杂性, 项目建设的工期、 成本及质量3大目标难以平衡. 为了解决工程项目多目标优化问题, 本文以某项目工程为研究对象, 对工程项目施工过程进行研究, 并构建了工程项目多目标优化模型. 考虑到工程项目3大目标难以量化求解, 引入先进的PSO算法来解决工程项目多目标优化问题. 由于传统PSO算法在寻优过程容易陷入局部最优解问题, 本文采用最优位置策略与外部档案集维护来改进算法, 并完成工程项目实验分析. 在工程项目单个目标寻优测试中, 改进PSO算法相较于APSO算法、 YSPSO算法和LNCPSO算法, 收敛性能提升了37.65%,27.86%和17.65%. 在ZDT1基准函数测试中, 改进PSO算法耗时为7.120 s, 标准MOPSO算法耗时为8.654 s, 改进PSO算法综合性表现更好. 采用改进PSO算法求解多目标优化模型, 优化后工程建设成本由2 664万元下降到2 768.80万元, 工程项目建设周期目标由580 d下降到562 d. 由此可见, 本文采用的优化方案可以显著降低工程项目成本与工期, 提高工程项目建设效果. 不过本研究也存在不足, 并未考虑工程风险、 安全等目标, 后期应该综合讨论这些因素, 以期进一步提高方案的有效性.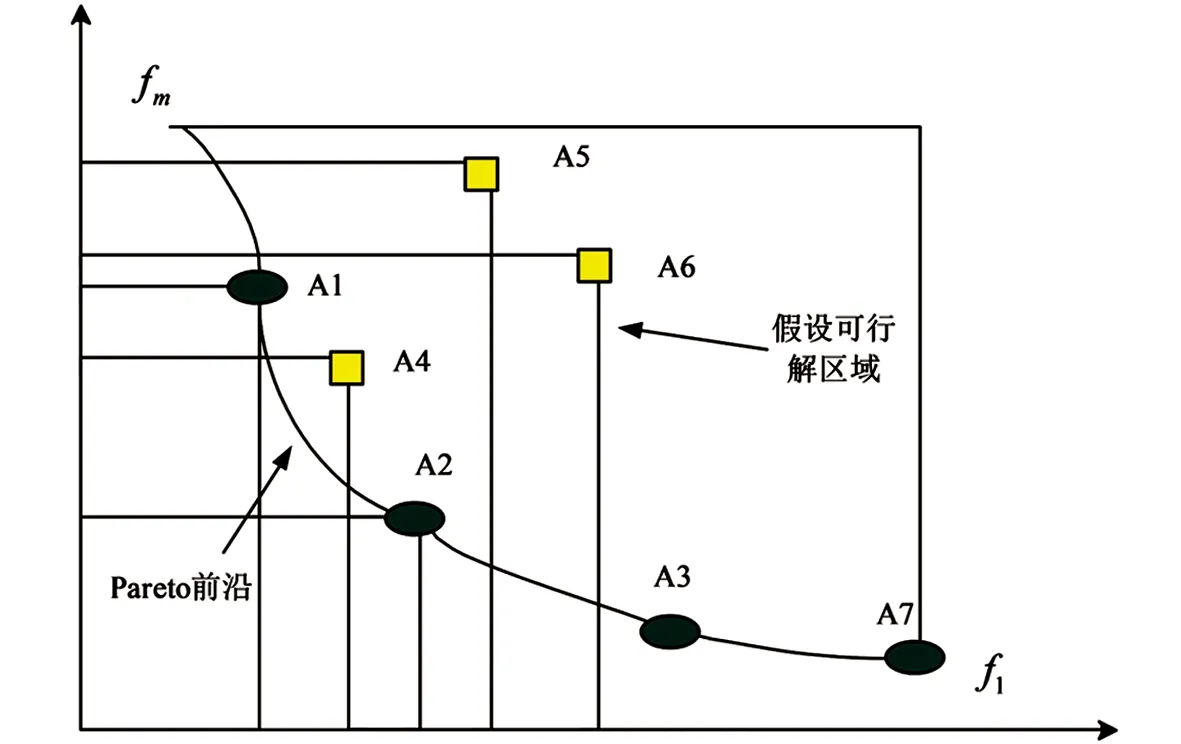
2 工程项目案例实验分析
2.1 改进PSO算法模型性能测试
2.2 工程项目多目标优化实验分析
3 结论

