一种面向蒙皮对缝测量的双线结构光标定方法*
鲁小翔,黄 翔,李 根,赵子越,孟亚云
(1.南京航空航天大学机电学院,南京 210016;2.南京航空航天大学苏州研究院,苏州 215000;3.航空工业北京长城计量测试技术研究所,北京 100095)
对缝特征广泛存在于飞机蒙皮表面,是飞机表面平滑度的主要评价指标。随着飞机隐身及气动性能的提高[1–2],传统蒙皮测量方法已经难以满足实际测量需求。线结构光三维视觉测量是一种借助线结构光平面重建待测特征空间信息的技术,其以抗干扰能力强、精度高且非接触等优点,正越来越广泛地应用于飞机蒙皮对缝特征的测量。
待测特征三维空间信息的重建精度是保证测量精度的前提,而线结构光平面的标定精度是保证待测特征重建精度的关键。近年来,对线结构光平面标定的研究主要集中在高精度的光平面拟合控制点的获取上。常见的方法有周富强等[3]利用一维靶标上基准点的距离及方向约束,基于消隐点原理解算出一维靶标在相机坐标系中的直线方程,最后由射影变换和直线方程获得待标定光平面上的拟合控制点;韩建栋等[4]提出基于三点透视(P3P)原理,利用标定靶标上3 个等距的共线点解算出待标定光平面上的拟合控制点;Wei 等[5]提出利用已知等距的平行线求取平面消隐线的原理完成拟合控制点的提取。上述方法常用于大视场的线结构光平面标定,且标定过程中获取的光平面拟合控制点数量较少,标定方法鲁棒性较差。Wu[6]和Zhou[7]等提出利用相机标定过程中获得的外参数拟合靶标平面,再以靶标平面上的特征线与光条的交点为拟合控制点。该方法需要通过相机标定来获取靶标平面在相机坐标系中的位姿,标定过程较为繁琐,且该方法获取的拟合控制点为相关特征的交点,仍存在拟合控制点数量少的问题。Dewar 等[8]提出拉丝法,此方法通过提取结构光光平面与细丝干涉后形成干涉亮点来获取拟合控制点;段发阶等[9]提出使用结构光光平面与锯齿形三维靶标干涉后形成的转折点来获取光平面拟合控制点,上述方法所需标定靶标精度要求高、制造难度较大。陈天飞等[10]提出基于机器人的自标定方法,该方法依靠机器人自身的高精度运动,构建附加约束,完成拟合控制点的提取;张曦等[11]提出的标定方法对机械运动精度要求高且标定过程复杂,难以广泛应用。
综上所述,当前标定方法存在拟合控制点数量少、标定靶标制造难度大以及标定过程复杂等,针对上述问题,本文提出一种基于二维靶标的双线结构光平面标定方法。该方法采用高精度快速位姿估计(EPnP)算法解算出相机与二维靶标平面之间的位姿关系,获得靶标平面在相机坐标系中的平面方程;依据相机的线面模型,解算出靶标平面上所有的拟合控制点集,在此基础上对上述点集进行去噪处理并使用特征值法对拟合控制点集进行拟合。该方法所需的二维靶标制造简单、精度高、维护和现场操作方便,更重要的是相对于传统方法易于获得丰富的拟合控制点,并能够对拟合控制点进行去噪处理,有益于提高结构光平面的标定精度及鲁棒性。
1 线结构光重建模型
线结构光三维测量系统主要由工业相机与激光器组成,如图1所示,其中Oc–XcYcZc表示相机坐标系,O–UV表示图像坐标系。设激光器发射的光平面1 与蒙皮对缝边缘的干涉端点P在相机坐标系下表示(xc,yc,zc),其在图像坐标系中的投影点p的坐标为(u,v),由针孔相机成像模型可得P点与p点之间的对应关系为[12]
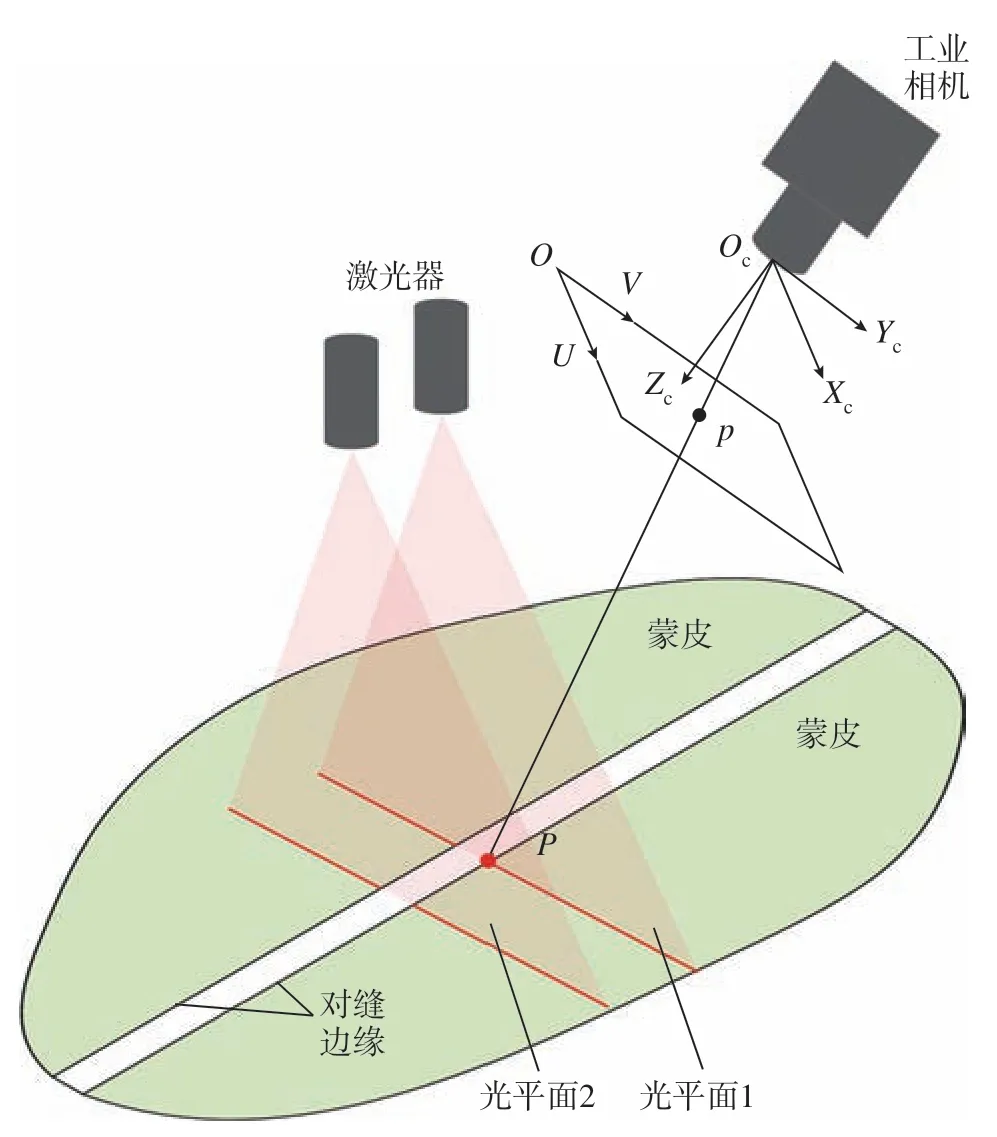
图1 线结构光重建模型示意图Fig.1 Diagram of line structured light reconstruction model
式中,fx、fy、u0、v0为相机内参数。设由激光器发射出的光平面1 在相机坐标系下的光平面方程可表示为
式中,A1、B1、C1和D1是结构光平面方程参数。依据相机的线面模型,联立式(1)与(2)可对图像中p点进行深度重建,获取其在相机坐标系中的对应空间点P的坐标。
使用线结构光重建模型恢复测量图像中相关特征的深度信息并代入蒙皮对缝测量模型,即可实现对蒙皮对缝间隙与阶差的测量。由图1 可得,测量模型所需的特征都在光平面上,如光平面1 与蒙皮对缝边缘的干涉特征点P,故而对光平面进行高精度、高鲁棒性的标定是保证蒙皮对缝测量精度的基础。
2 基于二维靶标的双线结构光标定方法

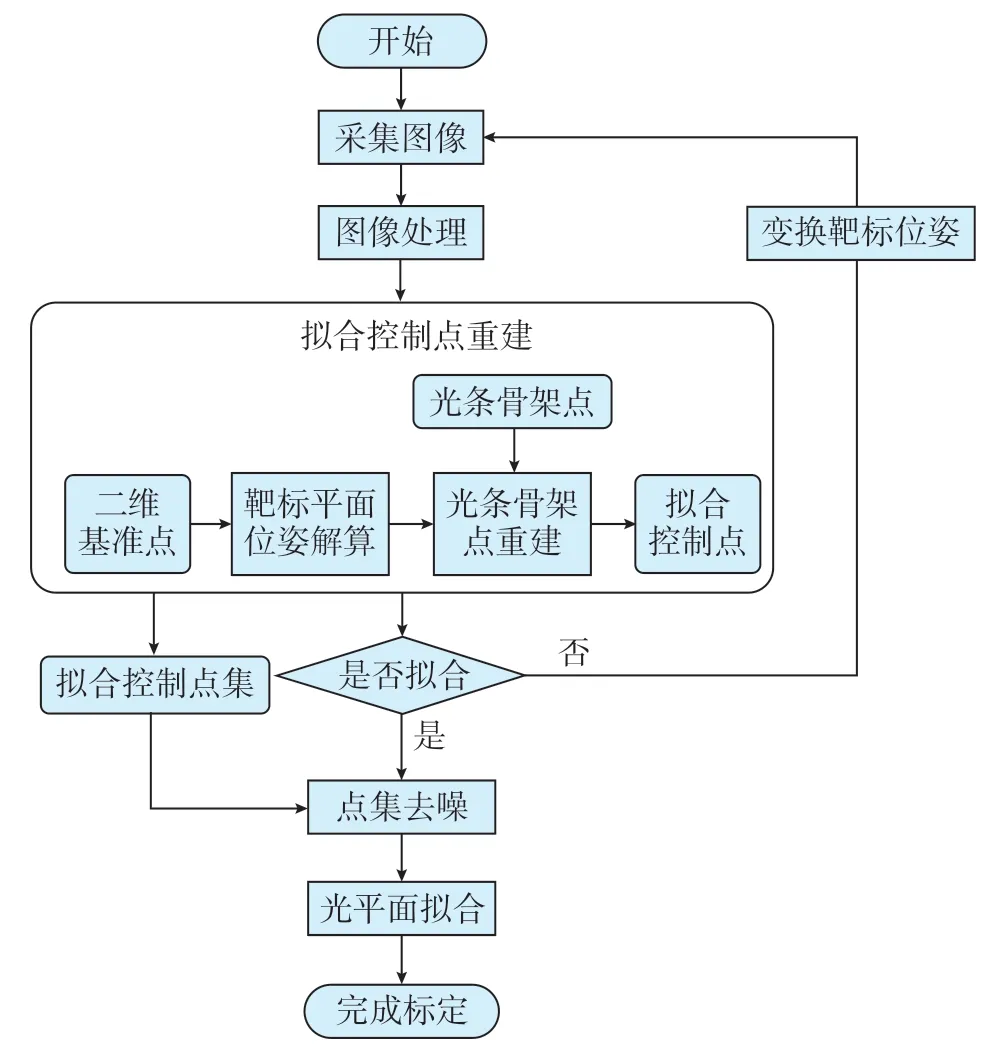
图3 标定流程图Fig.3 Calibration flow chart
2.1 靶标平面在相机坐标系下的位姿计算
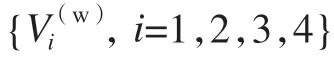
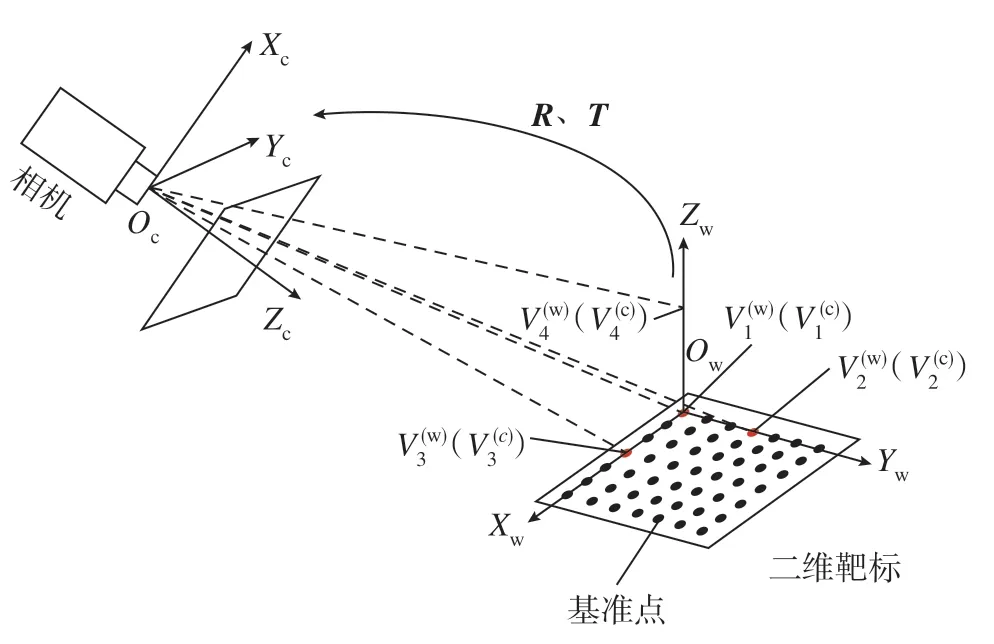
图4 位姿计算原理示意图Fig.4 Diagram of pose calculation principle
从世界坐标系到相机坐标系之间的转化为刚体变换,故可以得到在相机坐标系下,虚拟控制点与基准点之间的转换关系为
式中,sk为比例因子;K为通过离线标定获取的相机内参;fx、fy、u0、v0为相机内参数。由式(5)可得靶标平面上的基准点与其对应像点之间的转换关系为
将靶标平面上的4 个虚拟控制点在相机坐标系下的坐标与像素坐标相对应,可得到一个线性方程组为
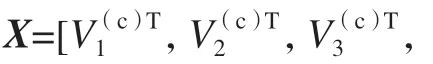
使用李代数ξ表示EPnP 方法获取的相机坐标系与棋盘格坐标系之间的转换关系R、T(其中R表示两坐标系之间的旋转矩阵,T表示两坐标系之间的平移矩阵);以ξ为变量建立的重投影误差模型为
2.2 拟合控制点在相机坐标系下坐标解算
获取相机坐标系与世界坐标系之间的转换关系R、T后,即通过
可获取靶标平面上的基准点在相机坐标系下的坐标,进而可拟合出基准点所在的φ平面(图5)在相机坐标系中的平面方程为
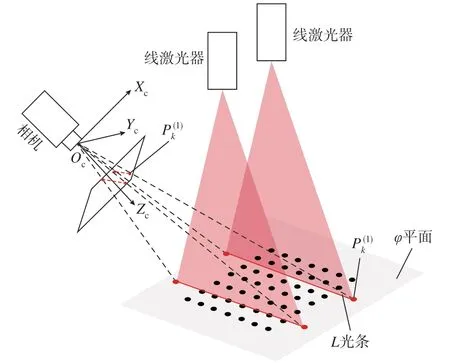
图5 光条重建示意图Fig.5 Reconstruction of light stripe
线激光器投射的光平面与靶标平面干涉后在φ平面上形成一条直线干涉光条L,通过图像处理,可在图像坐标系中获得呈直线分布的光条骨架点集{Pk(l),k=1,2,…,n}。由式(1)可知,图像中的任意像素点对应着相机坐标系中的一条射线,无法获取具体的空间坐标。
由于图像中的干涉光条是线激光器投射的光平面与φ平面干涉后形成,故光条骨架点对应的拟合控制点必在φ平面上。联立式(1)与(10),可计算图像中光条骨架点在相机坐标系中的三维坐标为

2.3 基于特征值法的光平面拟合
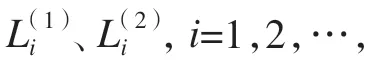
2.3.1 光平面拟合
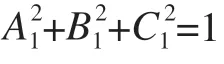
使用拉格朗日乘数法,组成函数,即
将式(13)分别对Al、Bl、Cl求导并令导数为0,从而获得特征值方程为
由式(15)可得,当λ最小时所对应的特征向量就是光平面1 的平面方程参数Al、Bl、Cl,同理可获得光平面2 的平面方程参数。
2.3.2 拟合控制点集去噪处理
由于图像噪声等因素的影响,重建后的拟合控制点集周边存在着大量噪声点。为进一步降低噪声点对平面拟合精度的影响,本文设计基于平面模型的RANSAC去噪算法。以图6 中的拟合控制点集为例,其具体拟合步骤如下。
(1)采集9 组标定图片,在当前相机坐标系下与之对应,同一光平面可获得9 条呈线性分布的拟合控制点集。在上述点集中随机选出3 个点,组成大小为27 的初始点集S,对点集S使用特征值法拟合初始平面方程,设其为
(2)计算所有拟合控制点到初始平面的距离,为
(3)计算dj的标准差σ,为
(4)重复步骤(1)~(3),设置迭代次数为iter;以M值最大时的t值为阈值,提取内点点集设为Sf。
(5)使用特征值法拟合点集Sf,获取待拟合平面方程。
由图6 可以看出,去除噪声后拟合的平面能够更好地贴合拟合控制点集。表1 为去噪前后的平面拟合参数对比,可得,去噪后平面的和方差(SSE)为23.53,相较于去噪前平面降低了77.83;去噪后平面的确定系数(R2)为0.9991,相较于去噪前提高了0.0068。
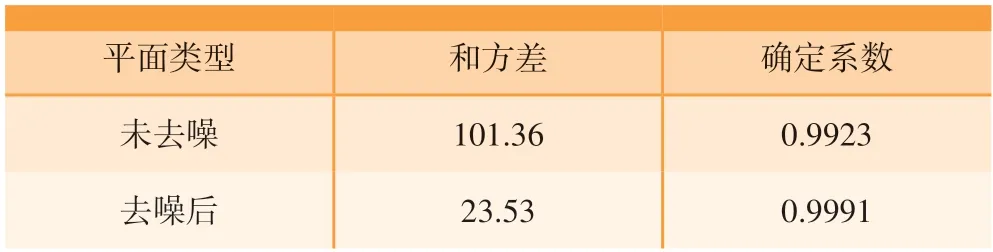
表1 平面拟合参数对比Table 1 Comparison of plane fitting parameters
3 试验与分析
3.1 标定试验
试验采用大恒图像的MER–502–79U3C 水星工业相机,分辨率为2448 pixel×2048 pixel,镜头为Computar M0814–MP2。线激光器的波长为635 nm,输出单个光平面,出光夹角为60°。使用两个单线激光器以及一台工业相机组成蒙皮对缝测量试验平台,如图7所示。
使用张正友相机标定算法对相机进行离线标定,得到其标定参数如表2所示。
试验过程中保持双线结构光测量平台固定不变,调整相机视野中的靶标平面的位姿,拍摄9 组试验图像。为了保证图像中靶标平面上的基准点与光条骨架提取的精度,对同一位姿的靶标平面进行不同曝光采集;具体做法如下。
(1)打开激光器,将相机曝光时间调整为30 μs,采集激光器投射的光平面与靶标平面干涉后形成的光条图像。
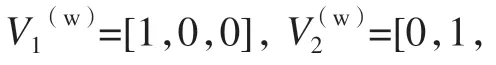

表3 靶标坐标系与相机坐标系之间的转换关系Table 3 Transformation relationship between target coordinate system and camera coordinate system
通过上述靶标坐标系与相机坐标系之间的转换关系,可以获得靶标平面上的基准点在相机坐标系中的空间坐标;进而可获得各个位姿下靶标平面在相机坐标系中的平面方程,从而将基准点扩展为基准面,其平面参数如表4所示。
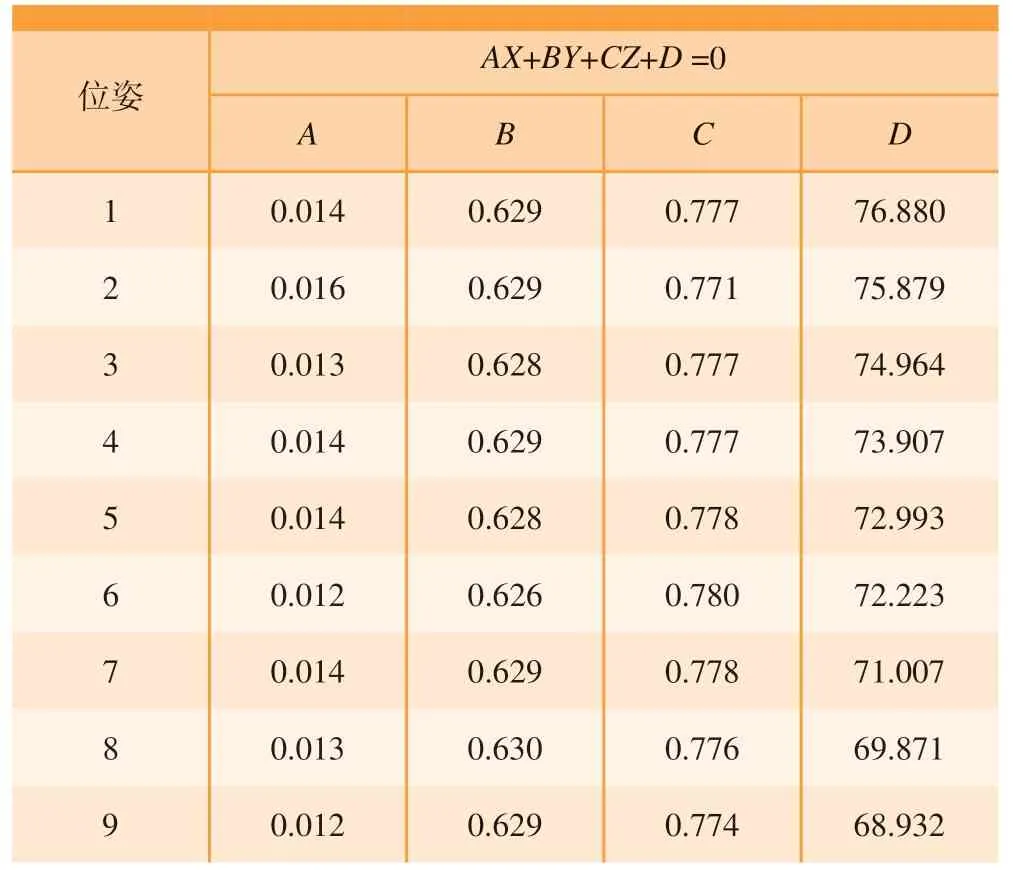
表4 靶标平面在相机坐标系中的平面方程Table 4 Plane equation of target plane in camera coordinate system
对采集的原始光条图像进行处理,获取光条骨架在图像坐标系中的像素点集,重建上述点集,即可获得光平面拟合控制点集。使用RANSAC 算法对属于同一光平面的控制点集进行去噪处理,迭代次数为100 次,最后使用特征值法拟合所有内点,获取待标定光平面方程,如图8所示。
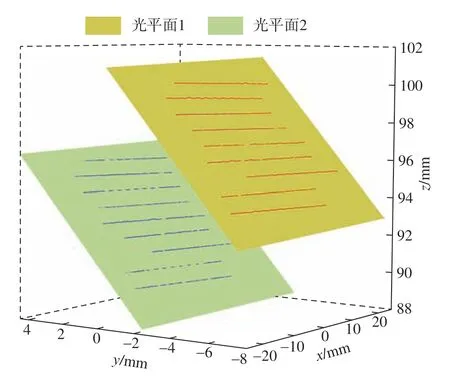
图8 光平面拟合图Fig.8 Picture of fitting results of light plane
传统的标定方法中,基于三点透视的结构光标定算法[4]能够同时标定两个结构光光平面,且与本方法一样,都是基于二维靶标对结构光光平面进行标定,故选用三点透视标定方法与本文中的方法进行对比。两种方法的标定结果如表5所示。
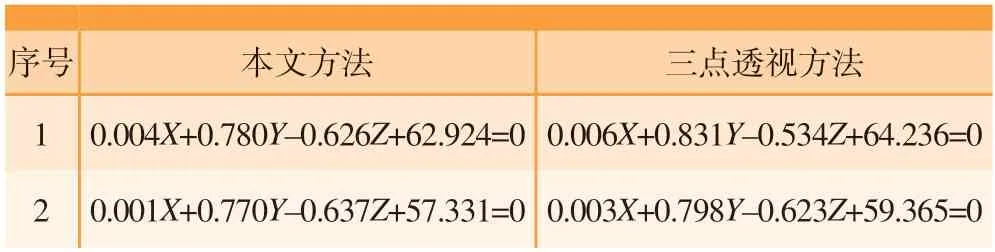
表5 结构光光平面方程Table 5 Plane equation of structured light
3.2 标定精度验证对比试验
(1)蒙皮对缝间隙阶差测量模型。如图9所示,P1、P2、P3、P4为结构光平面与蒙皮对缝边缘干涉后形成的特征点,通过对测量原始图片进行处理,提取干涉特征点在图像坐标系中的坐标并将其代入式(1)和(2),即可重建出相应特征点在当前相机坐标系下的空间坐标。在空间点P1和P2一侧取n个骨架点并设为{Pα1,Pα2,…,Pαn},在空间点P3和P4一侧取n个骨架点并设为{Pβ1,Pβ2,…,Pβn};使用点集{Pα1,Pα2,…,Pαn}拟合α平面,使用点集{Pβ1,Pβ2,…,Pβn}拟合β平面;分别计算点集{Pα1,Pα2,…,Pαn}到β平面的距离,点集{Pβ1,Pβ2,…,Pβn}到α平面的距离,通过求取上述距离的均值即可获得蒙皮的对缝阶差,为
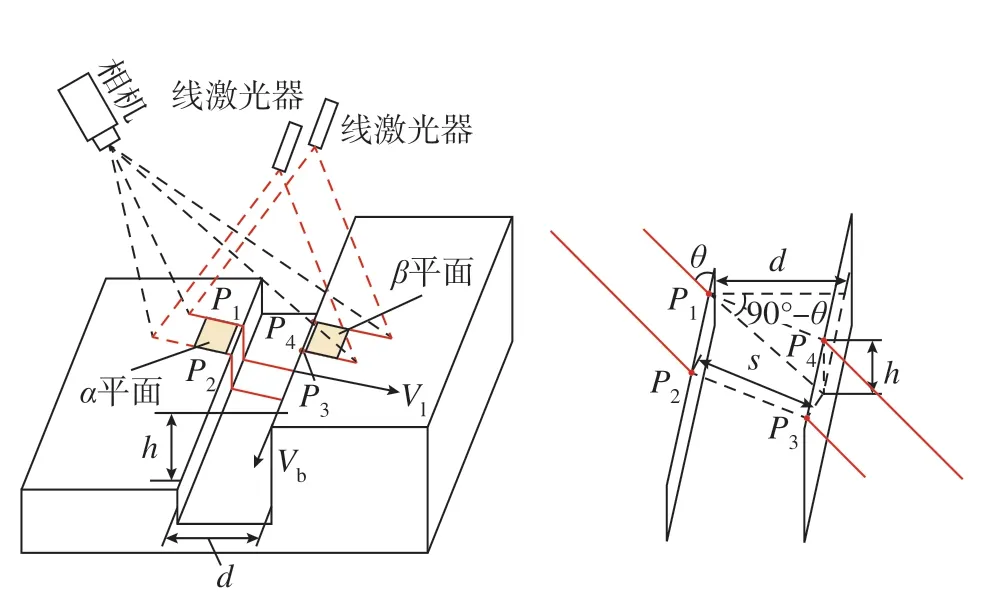
图9 对缝间隙与阶差解算模型Fig.9 Calculation model of seam gap and seam flush
设向量Vb表示蒙皮对缝边缘的方向,干涉光条的直线方向为Vl,由此可得干涉光条与对缝边缘之间的夹角θ为
点P1与点P4之间的距离和点P2与P3点之间的距离相等并将其设为s;通过式(19)可计算出对缝的阶差h,从而得出对缝间隙为
(2)标定精度验证。为验证本文中提出的结构光系统标定算法的标定精度,设计对缝测量标准块(图10)。标准块制造完成后,使用先临三维高精度蓝光扫描检测系统(测量精度5 μm)对其进行复测,选取试验件中8 条对缝进行试验,试验对缝的实测结果如表6所示。

表6 对缝测量标准块实测数据Table 6 Measured data of standard block for seam gap measurement mm
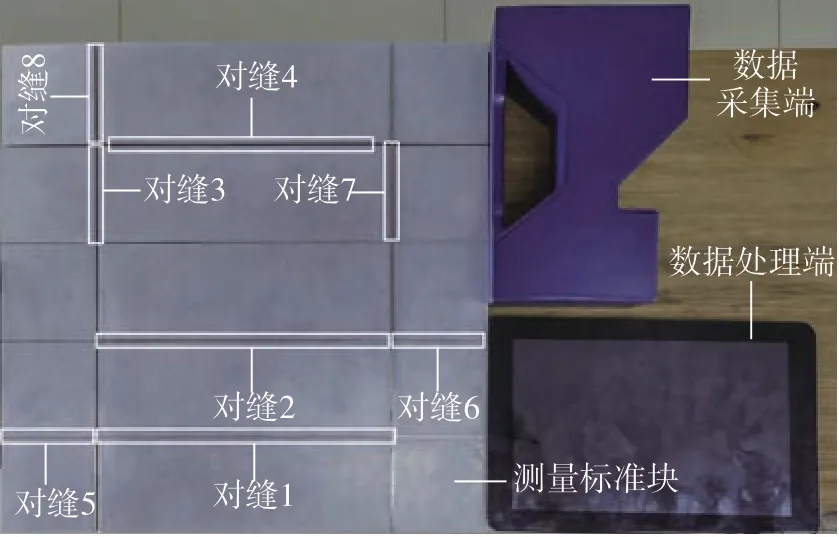
图10 精度验证系统Fig.10 Accuracy verification system
使用表5 中的两组标定参数分别对标准块进行测量试验。每组试验测量8 条对缝,每条对缝分别进行20 次采样测量,试验结果如图11、表7 和8所示。
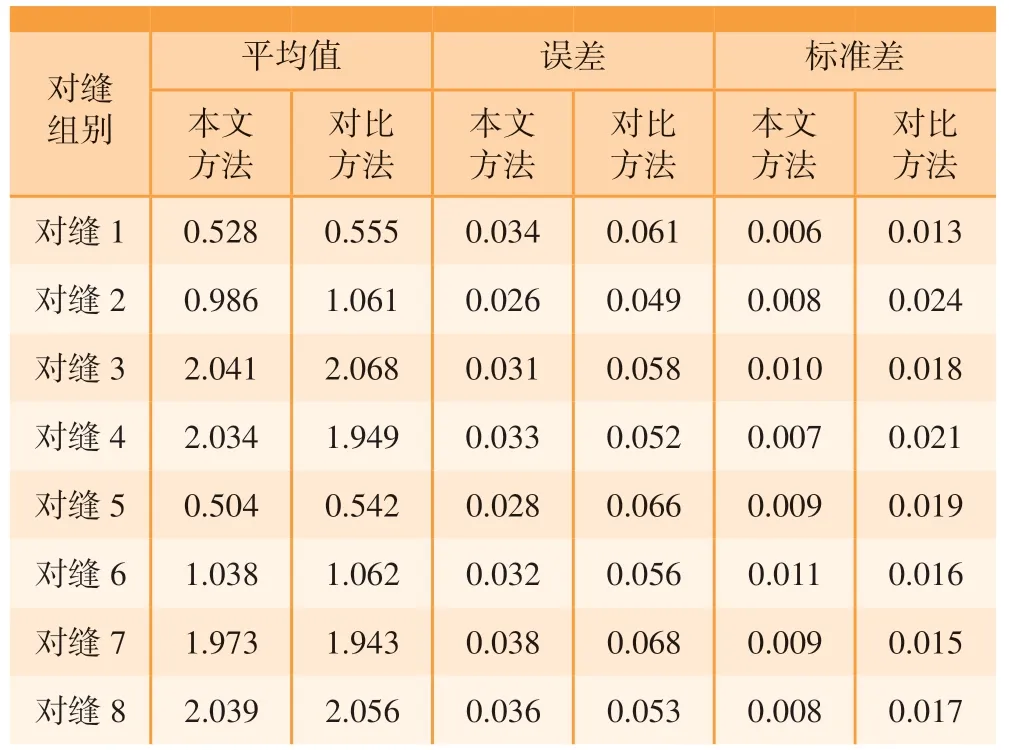
表7 对缝间隙试验结果Table 7 Seam gap experiment results mm
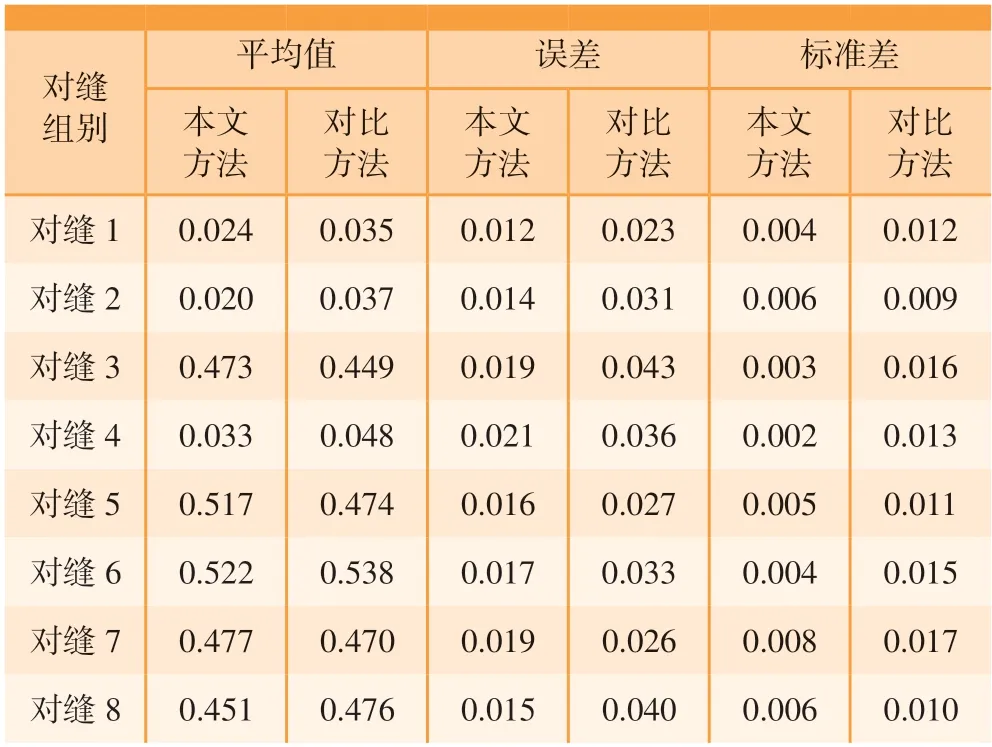
表8 对缝阶差试验结果Table 8 Seam flush experiment results mm
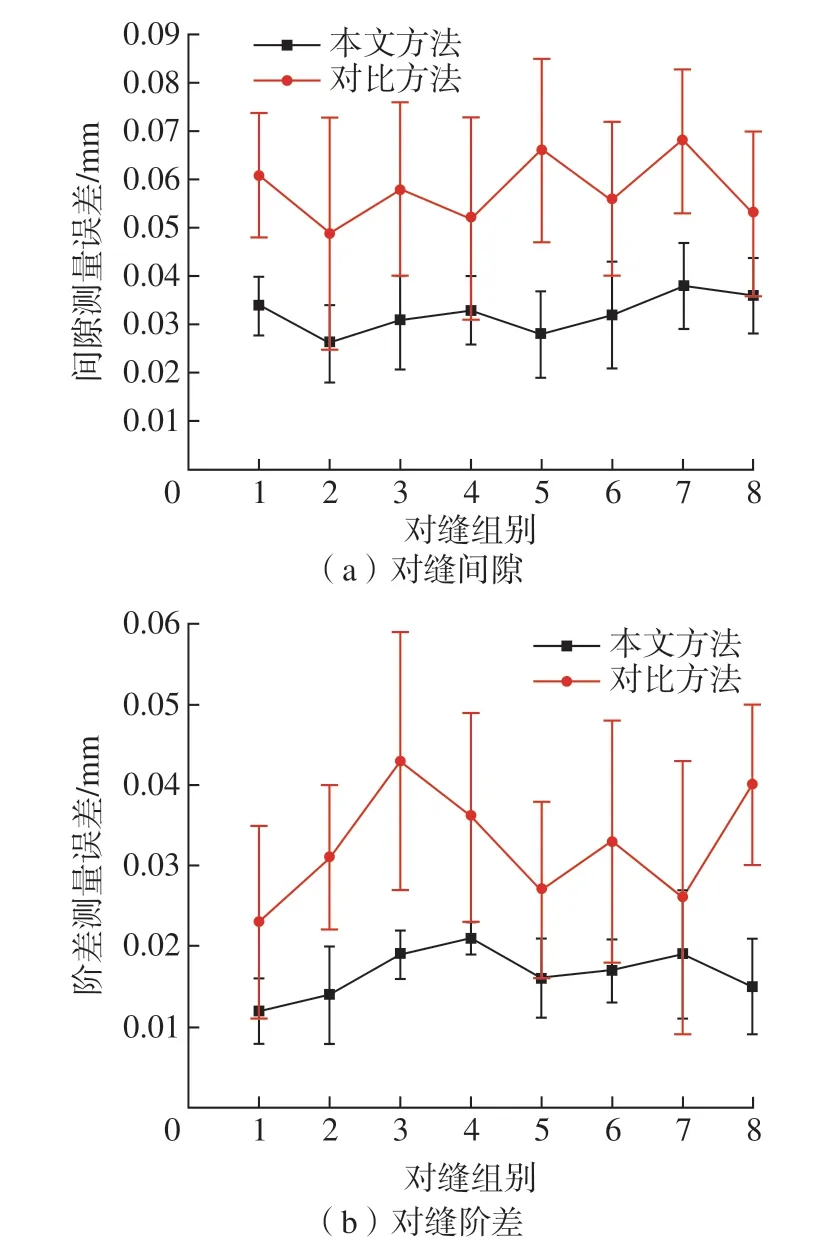
图11 对缝间隙与阶差测量误差Fig.11 Measurement error bar of seam gap and seam flush
由表7 和8 可知,使用本文所提方法标定后的系统的蒙皮对缝间隙测量精度优于0.050 mm,对缝阶差的测量精度优于0.030 mm;而基于三点透视方法标定后的系统的对缝间隙测量精度优于0.090 mm,对缝阶差的测量精度优于0.060 mm。对比可得,对缝间隙的测量精度提高了0.040 mm,对缝阶差测量精度提高了0.030 mm。与此同时,由图11 可得,使用本文所提方法标定后的系统在测量稳定性方面也有所提高。
4 结论
传统光平面标定方法仅利用靶标上有限的基准点来获取光平面拟合控制点,从而导致拟合控制点数量较少,且空间分布规律受光条图像处理算法的影响较大。本文以靶标平面上的基准点为输入,基于EPnP 算法构建靶标平面姿态计算模型,深入挖掘基准点所包含的位姿信息,将靶标平面上的基准点信息转换为基准面信息。在此基础上,依据线面约束,将当前位姿下靶标平面上的所有光条特征转换为拟合控制点。变换标定板位姿,即可获得丰富的光平面拟合控制点;对上述拟合控制点进行迭代去噪处理,并同时考虑多个方向上的误差来拟合待标定光平面,减少了噪声对拟合精度的影响,提高了光平面拟合的鲁棒性。在实验室环境中对测量标准块进行测量试验,试验表明,使用本文所述的方法标定后的双线对缝测量系统的间隙重复测量精度优于0.050 mm,阶差重复测量精度优于0.030 mm,相对于三点透视标定方法的测量结果有较大幅度的提高,能够满足实际场景的使用需求。

