方格纸中发现勾股定理

赵维坤 整理

据《周髀算经》记载，公元前11世纪，我们的祖辈就在生产实践中发现了“勾三股四弦五”的结论，这种结论用数学语言可以表述为：如果取勾的长度为3个单位，股的长度为4个单位，连结勾股两端的这条“弦”的长度恰好为5个单位，那么勾、股两条边一定相互垂直。这就是我们常说的“商高定理”（其实是勾股定理的逆定理）。

古人利用这个结论制造出了标准的测量工具——“矩”。有了“矩”，我们就能进行准确的测量。

今天，我们利用方格纸来重新发现勾股定理。

我们记下列图形中每个小方格的边长都为1。

首先，我们在方格纸中画出2条直角边长分别为1、2的直角三角形（如图1）。通过计算图中3个正方形的面积，我们能发现，直角三角形（阴影部分）的两直角边a、b和斜边c之间的关系：c2=2ab+1及a2+b2=c2。

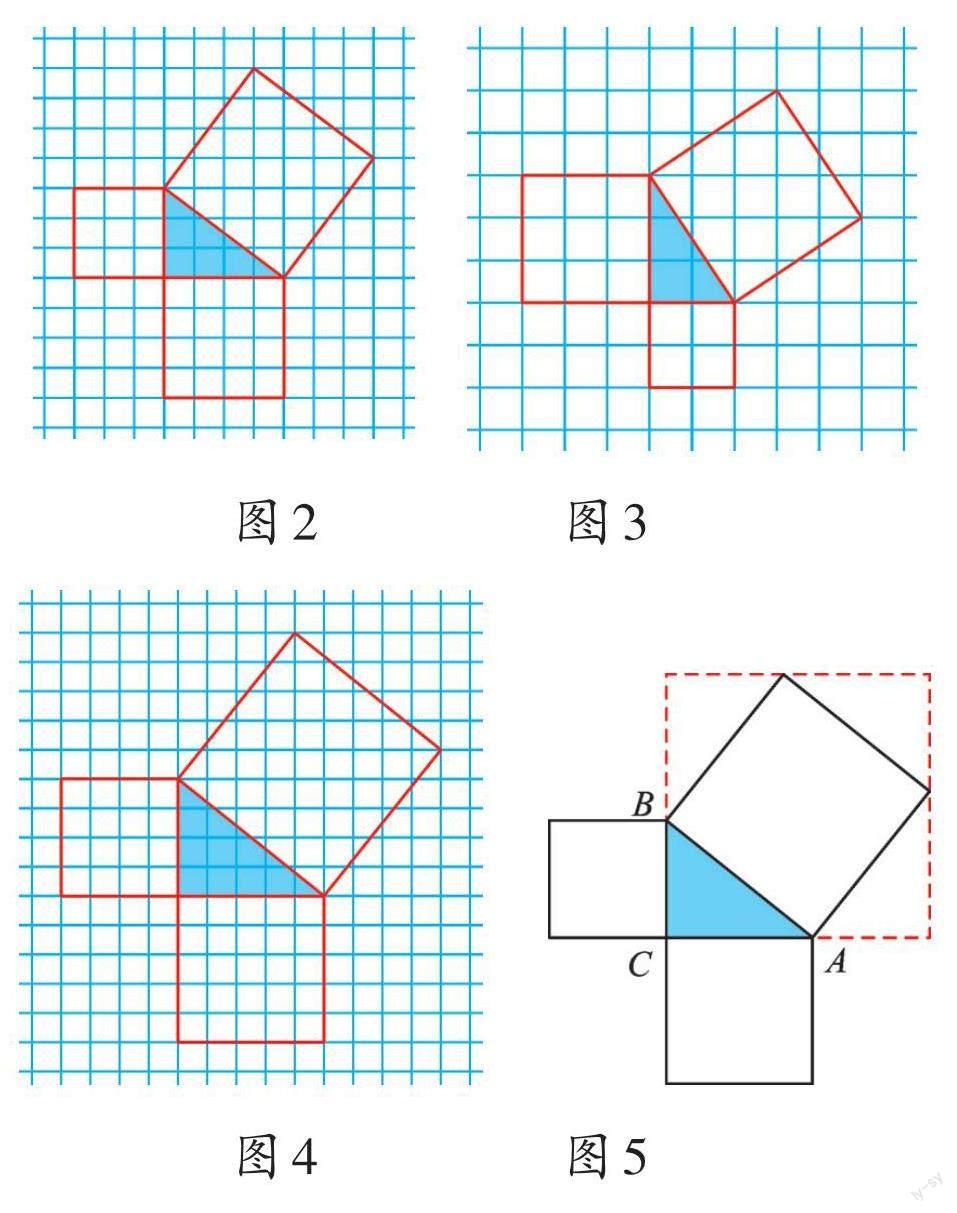
继续画直角三角形（图2—图4），这两个结论还成立吗？

要说明这两个结论正确与否，我们还要进行一般化证明。

把上图中的小方格背景撤去，并且隐去a、b的具体数值，在一般的直角三角形ABC中，已知∠ACB=90°，BC=a，AC=b，AB=c，a2+b2=c2是否同樣成立？（可以利用刚才计算斜边上正方形面积的方法证明这一命题的正确性。）

（作者单位：江苏省盐城市毓龙路实验学校）